空间机械臂的确定性学习控制

杨飞飞，王 聪，曾 玮

(1.华南理工大学自动化学院，广州510641;2.华南理工大学机械与汽车工程学院，广州510641;3.龙岩学院物理与机电工程学院，龙岩364012)

0 引言

随着空间技术的迅速发展，机器人机械臂［1－3］的作用日益重要。利用安装在航天器上的空间机械臂代替宇航员完成捕捉失效卫星、建造空间站、维修空间站以及大型空间站的在轨组装工作，能减少宇航员舱外活动，避免生命危险和节省出舱费用［4］。

在微重力环境下，机械臂空间操作时，往往会引起载体位姿的变化，从而表现出非完整的动力学特点，且系统动力学方程关于系统惯性参数呈非线性函数关系。同时，空间机械臂操作往往具有不确定性，如参数的摄动，负载的扰动及载体中燃耗等，而利用现有的空间机械臂动力学模型的先验知识常常难以建立其精确的数学模型［5］。自适应神经网络技术的发展为解决机械臂控制中存在的一些问题提供了新的途径［6－7］。针对动力学未知的非线性机械臂系统，自适应神经网络控制器［6］能保证系统状态最终一致有界以及跟踪误差的收敛。然而，由于不满足持续激励条件，所采用的神经网络不能实现对机械臂系统动态的准确逼近，以至于对经历过多次的同一控制任务，神经网络仍然需要重新进行冗余而繁琐的训练［7］。最近新兴的确定性学习理论［8］可实现对非线性系统(包括闭环非线性控制系统)的局部准确建模，以及对非线性系统产生的动态模式的快速识别。文献［7］采用确定性学习理论［8］，使用径向基函数(Radial Basis Function，RBF)神经网络为机械臂设计自适应神经控制算法，不仅实现了闭环系统所有信号的最终一致有界，同时实现了对未知机械臂闭环系统动态的局部准确逼近，并可将所学知识应用于后续相同或相似的控制任务中。

值得注意的是，空间机械臂在执行各种不同的任务当中，其惯性动力学会发生改变。这种改变使得对机械臂系统进行控制变得更加困难［9］。为了解决这个问题，多模型控制思想近年来被用于具有非线性动态的空间机械臂控制中［10－11］。尤其是，Goodwin［12－13］、Narendra［9，14］等人在基于模型切换的多模型自适应控制器设计方面取得了很多成果，为基于模式的空间机械臂控制提供了研究思路。尽管如此，上述多模型自适应控制器的结果多局限于线性系统，很难推广到非线性系统。在最近新兴的确定学习理论中提出一种基于模式的控制思路［8，15－16］，即通过把非线性系统产生的不同周期或回归轨迹定义为动态模式，并在对动态模式进行快速识别的基础上，可选择相应的已经过训练的、包含了系统局部准确模型的常值神经网络控制器用于对非线性系统进行多模型控制。

本文研究针对一种空间机械臂的基于模式的控制方法，优点在于:1)由于采用确定性学习算法，可实现对空间机械臂未知非线性动态的局部准确逼近;对于新出现的任务模式，基于对其快速识别并调用相应的常值神经网络控制器对机械臂系统进行控制，可实现响应速度更快，跟踪性能更好的空间机械臂控制;2)空间机械臂基于模式的控制的切换发生在不同系统动态之间，不会因状态改变而发生频繁切换，因而可改善系统的暂态性能，从而保证系统较高的控制性能。最后，仿真结果表明控制方法的有效性。

1 问题描述

基座固定的空间机械臂动力学方程为［17］

式中:q，˙q，¨q∈Rn分别代表关节的位置、速度和加速度;M(q)∈Rn×n为对称正定的惯性矩阵;Vm(q，˙q)∈Rn×n为哥氏力和向心力矩阵;F(˙q)∈Rn为摩擦力矢量;G(q)∈Rn为重力矢量;τ∈Rn为控制转矩输入矢量。

空间机械臂的动力学方程(1)具有如下性质。性质1.惯性矩阵M(q)是正定对称矩阵，且有界，即满足m1I≤M(q)≤m2I，∀q∈Rn，其中，I为适当维数的单位矩阵，m2≥m1＞0。

令x1=q，x2=˙q，则式(1)可表示为

由此，本文考虑一类机械臂通用模型:

式中:x= ［x1，x2］T∈R2是系统的状态变量，f(·)和g(·)表示未知的非线性系统动态。

本文设计机械臂通用系统(3)跟踪由下面参考模型产生的不同跟踪任务:

式中:xd= ［xd1，xd2］T∈R2是状态变量是光滑的非线性函数m=1，2，…，M)表示由于初始条件和系统参数不同产生的不同参考轨迹(定义为不同的任务模式)。σ:R+=［0，∞)→S={1，…，M}是关于时间的连续分段函数，表示一类切换信号。M∈N+表示产生的不同任务模式的数目。

根据性质2以及性质3，以下假设成立。假设1.g(x)的符号已知且存在常数g1≥g0＞0使假设2.存在常数gd＞0使得g˙(x)≤gd，∀x∈Ω⊂R2，式中˙g(x)是关于时间的导数。

控制目标:给定多个跟踪任务，设计基于模式的局部RBF神经网络控制器，实现机械臂系统基于跟踪任务模式的控制。

2 机械臂系统基于模式的神经网络控制器设计

空间机械臂系统要求实现沿参考轨迹(称为参考任务模式)的运动，当有多个参考轨迹时，需要首先识别出当前的参考轨迹，然后调用相应的神经网络经验控制器对机械臂系统进行跟踪控制。机械臂系统基于任务模式的控制过程可描述如下:

自适应神经网络控制器设计为:

式中:z2=e2/g(x)，e1=x1－xd1，e2=x2－xd2，c2为控制器增益。

神经网络自适应律为:

上述自适应神经网络控制器的设计在专著［8］中已有详尽的研究，并总结于第四章定理4.5。

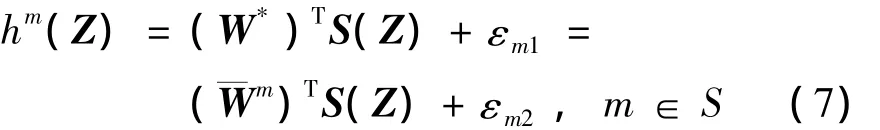
εm1，εm2为逼近误差

本文依据上述辨识结果，构造出如下包含所学机械臂系统动态的常值神经网络控制器集合:

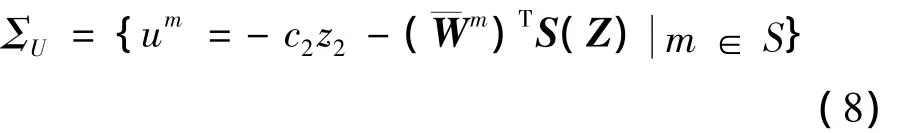
式中:¯xm=［x］T表示所构建的动态模型的状态，x是待识别任务模式的状态。B=diag(b1，b2)表示对角阵，注意bi(i=1，2)可选择为较大值。

采用下边的识别误差系统:

系统(10)是一个带有界扰动的简单线性时不变系统，由式(10)可快速识别任务模式，m ∈ S。在该步骤中，识别第m个参考模式所需时间用［tm，tm'］表示，且 tm＇=tm+ Δtm，Δtm＞ 0，m ∈ S 。

(3)基于对任务模式的快速识别和分类结果，选择神经网络控制器集合(8)中相应的控制器，对机械臂系统(3)进行闭环跟踪控制。

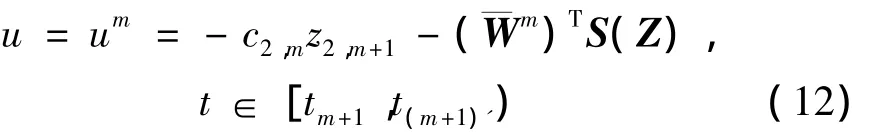
即未识别出模式φm+1dζ前，依然利用第m个控制器um对机械臂闭环动态进行控制。

3)模式识别完成后，控制器选取为:

综上，本文设计基于跟踪任务模式的控制器:

式中:m∈S，z1，m+1，z2，m+1分别表示机械臂动态跟踪第m+1个跟踪任务模式φm+1dζ的第一个误差分量和第二个误差分量，z2，m的定义类似，c2，m，c2，m+1分别表示um和um+1的控制器增益。

如果t0代表系统(3)的初始运行时刻，(im，tm)表示第σ(tm)个子系统动态当前活动，则基于跟踪任务模式的机械臂闭环控制系统可用一类切换序列来描述，如切换序列 Ξ ={(i0，t0)，…，(in，tn)，…，|in∈S，n∈N+}。本文对由机械臂闭环系统(3)，参考轨迹模式(4)，神经网络控制器集合(8)构成的基于模式的机械臂控制系统进行稳定性分析。首先给出以下引理。

引理1［18］.切换系统˙x=Aix，i=1，2，…，N若具有形为V(x)=xTPx的共同李亚谱诺夫函数，且对于i=1，2，…，N，˙V(x)关于时间负定，则切换系统对任意的切换序列指数稳定。

定理1.考虑基于模式的机械臂控制系统，包括被控对象(3)，参考轨迹模式(4)，以及基于模式的控制器(14)。对于由初始条件0)产生的参考轨迹模式m∈S):基于模式的机械臂闭环控制系统(3)中的所有信号有界，且系统状态跟踪误差~x=x(t)－xd(t)指数收敛到零的一个小邻域内。证.由于神经网络经验控制器(8)只在各自的训练域Ωφm，m∈S内有效，是一种局部的控制器，因此本文分两种情况讨论空间机械臂系统的稳定性。这里假设机械臂闭环系统(3)跟踪各个任务模式的切换瞬间的切换域均处于Ωζ之内。

(1)情况1:识别当前测试模式φm+1dζ，控制器取为

且神经网络训练区域满足:Ωφm+1⊂Ωφm，m∈S，即第m+1个模式的神经网络学习区域Ωφm+1包含于第m个模式的学习区域Ωφm中。

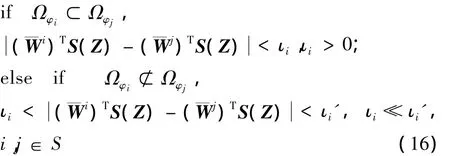
式中:

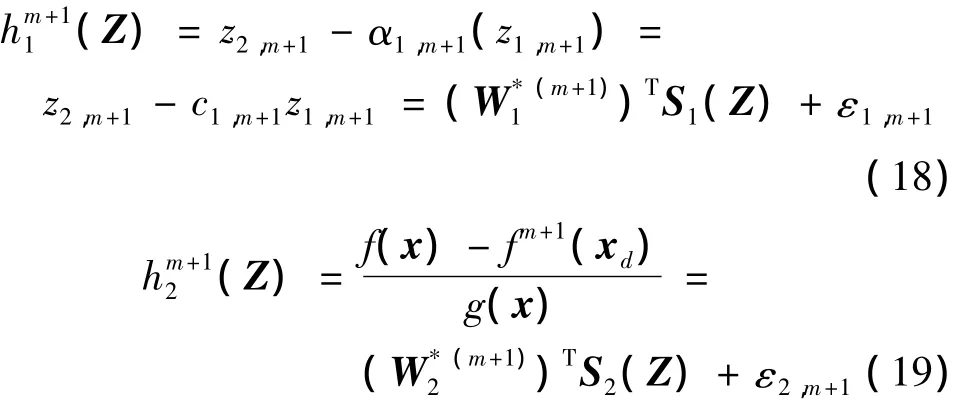
且李雅普诺夫函数取为

则有

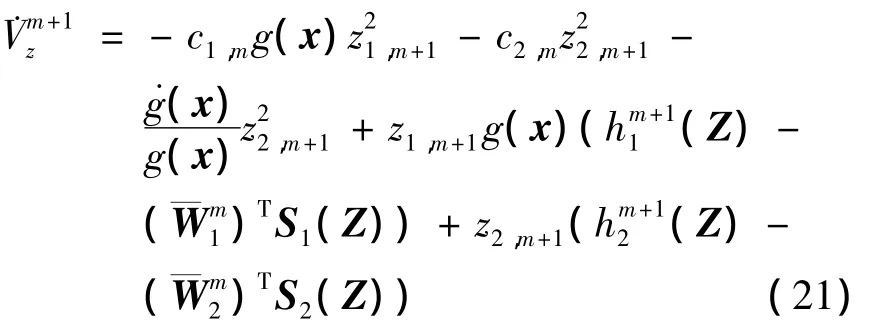
由于下边的不等式成立

因而得到

式中:ο1，m+1=O(ε1，m+1)，同理，

将式(24)(25)代入式(22)可得

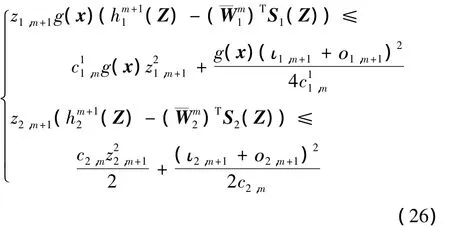
将式(26)代入式(23)，并根据假设1和假设2，得到

上式意味着

式中:

根据式(20)及(29)，进一步有

这意味着在［tm+1，t(m+1)'］内，通过恰当选取第m个证在短暂识别过程中能量函数是负定的。

动态过渡过程结束后，控制器切换为um+1，此时的机械臂误差动态方程为

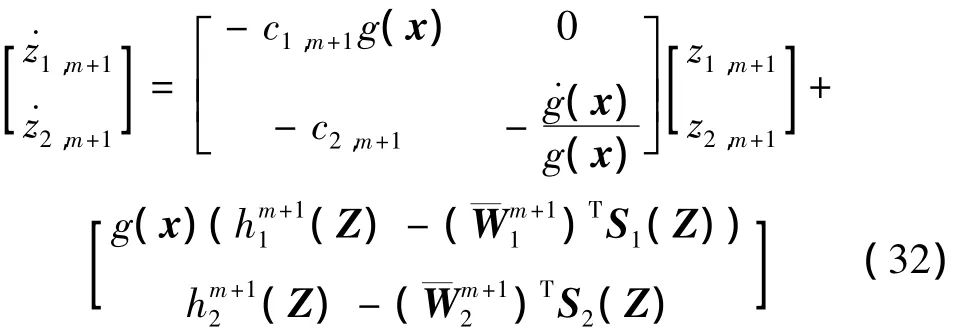
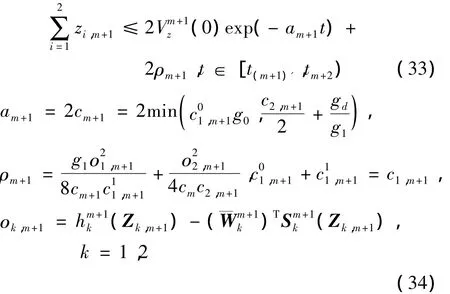
这就意味着，当 t∈ ［t(m+1)'，tm+2)时， zm+1≤此通过恰当选取参数致有界，并最终指数收敛于零的一个小邻域内。

神经网络训练区域满足:Ωφm+1⊄Ωφm，m∈S。

此情况与情况1分析方法类似，但在时间区间 t∈ ［tm+1，t(m+1)'］内采用控制器 umhigh，根据式(16)有

采用类似于情况1中的证明步骤，仍然有式(33)成立。与情况1不同的是，此时的参数

3 仿真校验

下面以基座固定的两联杆空间机械臂为例说明所提方法的有效性。两联杆机械臂动态方程(1)满足

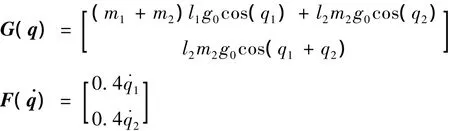
机械臂系统的实际参数值选取为:l1=1 m，l2

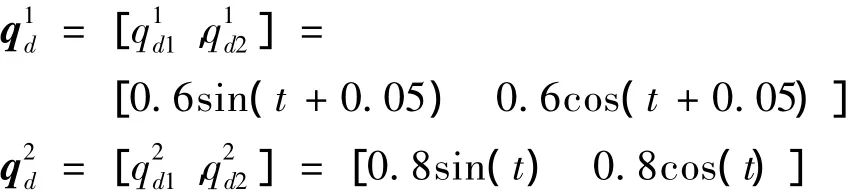
切换序列如图1所示。显然:第二个任务模式的神经网络学习区域Ωφ2不包含于第一个模式的学习区域 Ωφ1中，即 Ωφ2⊄Ωφ1(满足定理1 情况2)，因此需要选取高增益的控制器。

图1 跟踪不同的参考模式的切换序列Fig.1 Switching sequence of tracking different orbits

机械臂闭环系统的控制器参数均选取为:神经元的个数为3×3×3×3×4×4=1296个，均匀地分布在［－1.05，1.05］×［－1.05，1.05］×［－ 1.05，1.05］× ［－ 1.05，1.05］ × ［－ 1.05，1.05］×［－1.05，1.05］区间上，==16=100，Δt＜5 s。图2为跟踪两个任务模式的空间逼近效果图。图3为误差跟踪性能曲线，图4为跟踪误差曲线，图5为控制输入。

图2 空间上的函数逼近效果Fig.2 Function approximation in state space

从仿真结果看出，采用基于跟踪任务模式的常值神经网络控制器，可成功驱动仿真系统的状态收敛于参考状态附近的一个小邻域中，而且在跟踪过程中实现了确定学习。图2～图5清晰反映了切换瞬间，即60 s时刻，由于出现跟踪任务，而系统仍采用跟踪时的控制经验对机械臂系统进行控制，导致系统能量突增，出现了较大的摄动。经过短暂的识别过程后，机械臂系统立即调用跟踪参考任务练得到的经验控制器，这使得进入Ωφ2中的控制器能够马上利用在该区域内学习过的知识，响应速度与自适应控制器相比，加快许多。如图3～图4体现出了系统良好的跟踪控制性能，整个基于参考任务模式的机械臂系统指数稳定，且切换瞬间的暂态有界性利用短暂高增益控制器得到了保证。

4 结论

图3 状态x的跟踪性能Fig.3 Tracking performance of x

图4 状态x的跟踪误差Fig.4 Tracking error of x

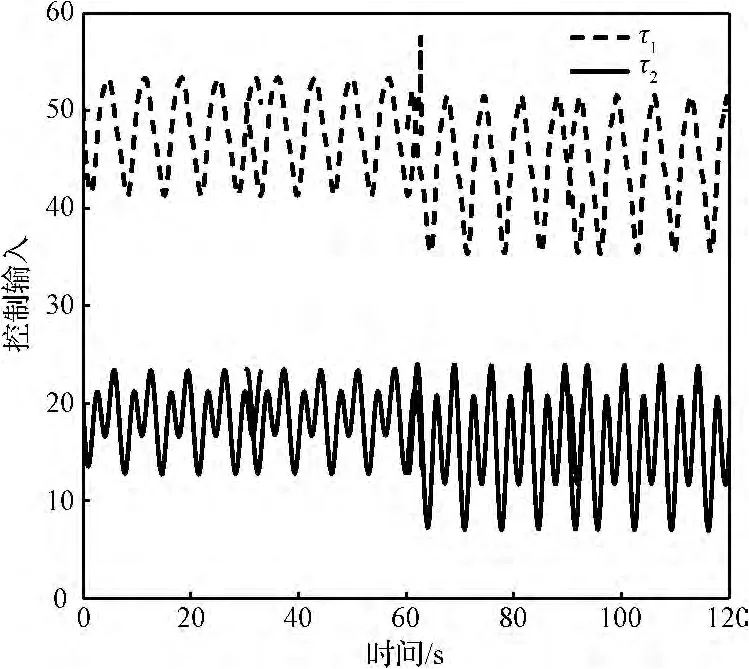
图5 控制输入Fig.5 Control input

研究了一类空间机械臂系统的确定学习控制方法，采用确定学习中基于模式的控制思想实现了空间机械臂基于模式的控制。通过理论证明，采用基于模式的局部神经网络控制器，机械臂闭环系统不仅能实现稳定性要求，而且在节省时间和能量方面也体现了优越性，同时说明这类基于任务模式的神经网络机械臂闭环系统由于具有慢切换的属性，因而可避免频繁切换。最后，仿真结果在基座固定的两联杆空间机械臂上进行校验，说明该方法的有效性。

［1］ Piltan F， Sulaiman N， Rashidi M， et al. Design and implementation of sliding mode algorithm:applied to robot manipulator-a review［J］.International Journal of Robotics and Automation，2011，2(5):265－282.

［2］ Piltan F，Sulaiman N，Marhaban M H，et al.Design of FPGA-based sliding mode controller for robot manipulator［J］.International Journal of Robotics and Automation，2011，2(3):183－204.

［3］ Piltan F，Sulaiman N，Nasiri H，et al.Novel robot manipulator adaptive artificial control:design a novel SISO adaptive fuzzy sliding algorithm inverse dynamic like method［J］.International Journal of Engineering，2011，5(5):399－418.

［4］ 洪炳熔，柳长安，李华忠.自由飞行空间机器人捕捉运动目标的力矩控制算法及其仿真［J］.宇航学报，2000，21(4):64－70.［Hong Bing-rong，Liu Chang-an，Li Hua-zhong.The torque control algorith of the capture of moving target of free flying space robot and its simulation ［J］. Journal of Astronautics，2000，21(4):64 －70.］

［5］ 洪在地，贠超，陈力.漂浮基空间机器人及其柔性影响下逆模神经网络控制［J］.宇航学报，2007，28(6):1510－1514.［Hong Zai-di，Yun Chao，Chen Li.Inverse model neural network control of free floating space robot under the influence of flexible［J］.Journal of Astronautics，2007，28(6):1510 －1514.］

［6］ 孙富春，孙增圻.机械手的神经网络稳定自适应控制器设计［J］.控制理论与应用，1997，14(6):809－816.［Sun Fuchun，Sun Zeng-qi. The design of stable neural network adaptive controller for the manipulator［J］.Control Theory and Applications，1997，14(6):809 －816.］

［7］ 吴玉香，张景，王聪.机械臂的自适应神经网络控制与学习［J］.机械工程学报，2013，49(15):42－48.［Wu Yuxiang，Zhang Jing，Wang Cong.Adaptive NN control and learning for the manipulator［J］.Journal of Mechanical Engineering，2013，49(15):42 －48.］

［8］ Wang C， Hill D J. Deterministic learning theory for identification，recognition and control［M］.New York:CRC，2009.

［9］ Narendra K S，Balakrishnan J，Ciliz M K.Adaptation and learning using multiple models，switching，and tuning ［J］.IEEE Control Systems，1995，15(3):37－51.

［10］ Ciliz M K.Combined direct and indirect adaptive control of robot manipulators using multiple models ［J］.Advanced Robotics，2006，20(4):483－497.

［11］ Nguyen-Tuong D，Peters J.Model learning for robot control:a survey［J］.Cognitive Processing，2011，12(4):319 －340.

［12］ Morse A S，Mayne D Q， Goodwin G C. Applications of hysteresis switching in parameter adaptive control［J］.IEEE Transactions on Automatic Control，1992，37(9):1343 －1354.

［13］ Weller SR，Goodwin G C.Hysteresis switching adaptive control of linear multivariable systems［J］.IEEE Transactions on Automatic Control，1994，39(7):1360 －1375.

［14］ Narendra K S，Balakrishnan J.Adaptive control using multiple models［J］.IEEE Transactions on Automatic Control，1997，42(2):171－187.

［15］ Wang C，Hill D J.Learning from neural control［J］.IEEE Transactions on Neural Networks，2006，17(1):130 －146.

［16］ Wang C，Hill D J.Deterministic learning and rapid dynamical pattern recognition ［J］.IEEE Transactions on Neural Networks，2007，18(3):617－630.

［17］ Lewis F L，Abdallah C T，Dawson D M.Control of robot manipulators［M］.New York:Macmillan，1993.

［18］ Narendra K S，Balakrishnan J.A common lyapunov function for stable LTI systems with commuting a-matrices［J］.IEEE Transactions on Neural Networks and Learning Systems，1994，36(12):2469－2471.