小型管壳式换热器壳侧换热CFD分析
龙隽雅 刘刚 甘长德
东华大学环境科学与工程学院
小型管壳式换热器壳侧换热CFD分析
龙隽雅刘刚 甘长德
东华大学环境科学与工程学院
本文运用CFD软件Fluent对小型管壳式换热器壳侧流场和温度场进行数值模拟,研究不同数量折流板(即不同折流板间距)对于换热器压降大小和传热系数的影响。对比CFD模拟结果与Bell-Delaware实验数据,结果吻合良好,证明了本数值模拟的准确性。
管壳式换热器 CFD折流板 压降 传热系数
管壳式换热器在加工和石化行业占有超过65%的市场份额,通过合理选择其物理构型、几何参数、使用材料及“正确”的设计可实现恰当的管壳式换热器选择。但因存在泄漏及旁路,壳侧流动情况复杂[1]。本文研究小型换热器模型,忽略泄漏和旁路,选用单弓形折流板为壳侧流体导流[2]。其沿壳侧交错布置,支撑管束之外还可增大壳侧流体湍流度。
换热器设计常用参考为Kern模型和Bell-Delaware模型[3]。Kern模型较保守,适用于预设计选值;而Bell-Delaware模型能较准确估测壳侧几何构型对压降和传热的影响,发现设计缺陷,但无法指出缺陷所在。本文使用CFD方法,建立小型管壳式换热器模型[4],使用软件ANSYS Fluent 6.3和Gambit,将壳侧流场和温度场可视化。本研究采用三种壳侧入口流速,对比模拟结果与Bell-Delaware模型数据,确定最佳折流板间距。
1 管壳式换热器模型建立
本研究中,壳侧流体为水,为提高匹配度,根据参考文献中饱和水蒸气热物理性质表,运用线性函数重新定义Fluent中常数水的物理参数。图1为本文研究的六块折流板的小型换热器模拟示意图,表1为该小型管壳式换热器的设计参数。
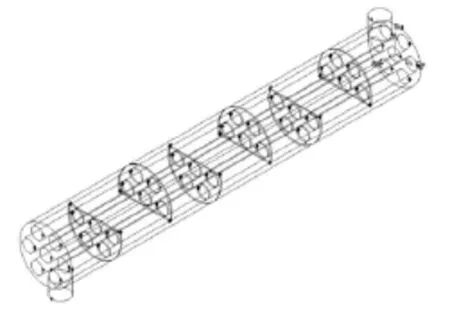
图1 六块折流板的小型换热器模拟示意图

表1 小型管壳式换热器设计参数
流动问题在数值计算前需求解连续性方程和动量方程。本文考察换热器温度场,故需另求解能量方程。表2为本文采用的数值模拟控制方程。

表2 数值模拟控制方程
表2各式中:ρ是空气密度;t是时间长度;U是合速度;u、v和w分别是速度矢量在x、y和z方向上的分量;p是流体微元体上的压力;τxx、τxy和τxz等是因分子粘性作用而产生的作用在微元体表面上的粘性应力τ的分量;Fx、Fy和Fz是微元体上的体力;keff是有效导热系数,Jj'是组分j'的扩散通量。方程右边的前三项分别描述了热传导、组分扩散和粘性耗散带来的能量疏运。源项Se为流体的内热源及由于粘性作用流体机械能转化为热能的部分,包括了化学反应热、辐射热、相间热量交换以及自定义的体积热源项目,有时简称其为粘性耗散相。
壳侧流体进口为速度进口,速度特征均匀,温度为300K,出口为压力出口,无压降;壁面为无滑移条件;换热器与外界绝热,壳侧无热流。因管侧流动易求解,故本文主要研究壳侧流动,模型中管为实心圆柱体[6],管壁温度为450K定温。
运用CFD数值模拟前需对物理对象进行建模和网格化分。本模型的面网格为四边形网格,体网格为四边形-杂交网格[7],用两种网格划分方式前处理6块折流板的换热器模型。粗网格约为700,000个;细网格约为1360,000个。
本模型壳侧流体流动为湍流[8]。湍流模型的选择目前也没有通用标准[9]。
本研究采用了Spalart–Allmaras模型[10]和两种不同的k-ε湍流模型。其中,Spalart–Allmaras湍流模型只需求解一个湍流方程,是ANSYS Fluent计算量最小、最经济的模型。标准k-ε双方程模型为基于漩涡粘度各向同性的假设基础上的半经验模型,经济、准确、适用范围广泛,其涡流粘度Cμ为常数。另有Realizable k-ε模型,其采用新湍流粘度公式,故Cμ为变量表达式。
通过CFD求解非线性方程组,将其离散化。离散方法分为有限差分法、有限元法和有限元体积法等[11]。其中,有限体积法因其计算的高效率,为商用的CFD软件采用,本文也选用此方法。
离散后生成对流-扩散问题的离散方程组。一阶和二阶迎风格式本文皆有相关模拟。一阶离散中,压力选用标准格式,动量、湍流动能和耗散率选用一阶迎风格式;二阶离散中,所有量都选用二阶迎风格式。压力残差收敛标准取为10-6,其他项残差取为10-3。
2 湍流模型和离散阶对CFD模拟结果的影响
本文采用六块折流板[11]的小型换热器模型进行研究,如图1。
一阶和二阶离散格式,以及三种不同的湍流模型(Spalart–Allmaras模型,标准k-ε模型和其修正式)分别用粗细两种网格密度来进行模拟,以考察湍流模型、离散阶及网格密度的选择对模拟结果的影响。模拟结果与Kern模型[12]和Bell-Delaware模型[13]的对比示于表3中,壳侧压降可直接由CFD导出得到[14],传热系数[15]通过对数平均温差(LMTD,log-mean-temperature-difference)的方法求得。

表3 CFD模拟结果与Kern模型和Bell-Delaware模型的对比(Nb=6)
分析表3,可知模拟结果全高于Kern模型值,是因Kern模型本身较保守,而模拟结果与Bell-Delaware模型拟合度较高,且质量流率越小拟合度越高。同时,模型选择对模拟结果有一定影响,这体现在不同模型结果与Bell-Delaware方法计算值的差别上。通过剔除差别较大的模型,得到与Bell-Delaware方法最相匹配的模型选择。
在B情况中,壳侧出口温度随着质量流量的增大而增大,总传热效率不符合常理,因此首先剔除。在A,D,D-2三种情况中,湍流模型为标准k-ε湍流模型,壳侧出口温度各异,但是总传热效率与Bell-Delaware的差别随着质量流量的减小而增大,因此也被剔除。C,E,E-2三种情况应用了k-ε湍流模型的修正式,壳侧出口温度随着质量流量的增大而降低,总传热效率的模拟结果也在预计范围内,其中,E情况为Bell-Delaware方法的最佳匹配模型,即修正式k-ε湍流模型,精细化网格的一阶离散格式。
整体看来,表3中的压降都低于分析计算值,究其原因,主要是因为折流板与壳侧直径之比B/DS=0.96满足推荐的给折流板开口为Bc=36%换热器的值。若折流板缺口面积比流体横截面小很多,模型就会低估压降大小。与文献[16]中提到的相反,Mukherjee[17]建议,最优化的B/DS应在0.3~0.6之间,本研究证明了B/DS值应在0.96上适当减小,故在分析中,对于已知长度的小型换热器,可减小B/DS值,即增大Nb值。
3 折流板间距对换热器压降和传热的影响
在折流板开口为36%时,本研究考察已知长度的换热器中四种不同数量折流板(即四种折流板间距)对壳侧流体压降和传热的影响。表4为四种模型的基本情况。

表4 不同折流板数的模型基本情况
模型采用修正式k-ε湍流模型,精细化网格的一阶离散格式,12块折流板模型达1568,850个网格[18]。四种模型分别用壳侧入口流体三种不同的质量流量来模拟,得到的12种结果列于表5中,各参数与Kern方法和Bell-Delaware方法的差值比列于表5中。

表5 不同的折流板间距和折流板数量

表6 对于折流板开口为36%时CFD模拟和数值计算的百分比差
由表6的结果可以看出,减少折流板间距(即增多折流板数量)[19],模拟结果与Bell-Delaware的匹配性提高,但与Kern方法的匹配性提升不明显。通过调节B/DS的比值,8,10,12块折流板与Bell-Delaware方法拟合良好,在质量流量为1kg/s时,两者之差可减小至10%以内。压降结果也有所改良,对于12块折流板的情况,差别小至10%。
在质量流量为1kg/s的情况下,四种不同数量折流板情况的速度路径曲线为图2~5。

图2 六块折流板时的流线

图3 八块折流板时的流线

图4 十块折流板时的流线

图5 十二块折流板时的流线
在图2和图3中,流体撞击折流板,流向改变,出现返流区域,折流板后部壳侧空间传热效果大大降低,影响总传热效率。而在图4和图5中,流体在壳侧空间充分发展,返流区域消失,传热效果良好,这一点在数据上也有所体现。因为Bell-Delaware模型为基于收集大量实验的换热器数据,因此必然有与实验最为吻合的一个CFD模型。
4 结论
1)考察不同网格划分精度、离散阶和湍流模型的选择对于结果的影响,将结果与Bell-Delaware方法计算值对比,可知修正式k-ε湍流模型,精细化网格的一阶离散格式为最佳模型。
2)Kern模型传热系数值总比模拟结果小。
3)Bell-Delaware模型与模拟结果吻合度高。对于传热效率,Bell-Delaware模型和模拟结果相差大多数情况下都小于2%,验证了Bell-Delaware模型在换热器设计领域的权威性。
4)高吻合也说明CFD是求解换热器流场和温度场的很好工具。随着计算机技术的发展,学者可用CFD技术模拟大型管壳式换热器,以帮助设计人员设计更佳性能的换热器。
[1]齐洪洋,高磊,张莹莹.管壳式换热器强化传热技术概述[J].压力容器,2012,(7):73-78
[2]董其伍,刘敏珊,苏立建.管壳式换热器研究进展[J].化工设备与管道,2006,(6):18-22
[3]刘明言,崔岩,黄鸿鼎.管壳式换热器工艺设计进展[J].石油化工设备,2003,(5):34-37
[4]刘天丰.非对称管壳式换热器结构分析及改进中的问题研究[D].杭州:浙江大学,2005
[5]文宏刚.管壳式换热器设计方法与数值模拟研究[D].上海:华东理工大学,2012
[6]林雄.管壳式换热器的流路性能数值模拟研究[D].广州:华南理工大学,2010
[7]王鹏.螺旋折流板管壳式换热器壳程流动与传热性能研究[D].济南:山东大学,2012
[8]付磊,唐克伦,文华斌.管壳式换热器流体流动与耦合传热的数值模拟[J].化工进展,2012,(11):2384-2389
[9]ANSYS.Fluent 6.3 User’s Guide[Z].New York:ANSYS Inc. [10]Spalart PR,Allmaras SR.A one-equation turbulence model for aerodynamic flows[Z].AIAA paper 92-0439
[11]郭崇志,林桥.管壳式换热器壳程流动与传热的数值模拟与验证[J].化工进展,2010,(10):2131-2140
[12]Kern DQ.Process Heat Transfer.New York:McGraw-Hill,1950
[13]Bell KJ.Delaware method for shell side design[A].In:Heat Exchangers:Thermal hydraulic Fundamentals and Design[C]. New York:Hemisphere,1981.581-618
[14]付磊,曾燚林,唐克伦.管壳式换热器壳程流体流动与传热数值模拟[J].压力容器,2012,(5):36-41
[15]古新.管壳式换热器数值模拟与斜向流换热器研究[D].郑州:郑州大学,2006
[16]Taborek J.Heat Exchangers Design Handbook(3)[M].New York:Begell House Inc.,2002
[17]Mukherjee R.Effectively design shell-and-tube heat exchangers [J].Chem Eng Prog,1998,94:21-37
[18]刘利平,黄万年.Fluent软件模拟管壳式换热器壳程三维流畅[J].化工装置技术,2006,(3):54-57
[19]王丹,董其伍,刘敏珊.管壳式换热器壳程特性数值模拟[J].南京工业大学学报(自然科学版),2009,(5):52-57
Shell Side CFD Analysis of a Small Shell-and Tube Heat Exchanger
LONG Jun-ya,LIU Gang,GAN Chang-de
College of Environmental Engineering Science,Donghua University
The temperature field and flow field inside the shell are resolved using CFD.The shell side design,especially the baffle spacing and baffle cut dependencies of the heat transfer coefficient and the pressure drop are investigated by numerically modeling a small heat exchanger.After contrasted,the difference between the CFD results with Bell-Delaware’s study in the heat transfer coefficient and the pressure drop is very small.In conclusion,the CFD results is accurate in this sense.
shell-and-tube,CFD,baffle,pressure drop,heat transfer coefficient
1003-0344(2015)06-064-4
2014-5-7
龙隽雅(1990~),女,硕士研究生;上海市松江区人民北路2999号东华大学4号学院楼环境学院3137室(201620);E-mail:silvergrey_l@sina.com

