基于相关法的分布式全相参雷达相干参数估计及相参性能

宋 靖 周青松 张剑云

1 引言

宽孔径、高功率的大规模相控阵雷达在远距离监视、跟踪以及目标识别中扮演着越来越重要的角色。然而随着对探测威力和精度要求的不断提高，大规模相控阵雷达的进一步发展面临着成本昂贵和机动不足等诸多因素的制约。分布式全相参（Distributed Aperture Fully Coherent, DAFC）雷达是继多输入多输出（MIMO）雷达之后出现的一种新体制雷达，它克服了大规模相控阵雷达的诸多固有缺点，是下一代雷达发展的技术方向。DAFC雷达的主要特点：多部机动式单元雷达或天线分散布设，通过对多部雷达回波进行信号级相参合成，等效形成一个大威力探测雷达。其关键性能包括：具有较高灵敏度，适用于远距离搜索、跟踪和目标识别，同时满足机动部署能力。DAFC雷达先后工作于两种典型模式：MIMO模式和全相参（Fully Coherent,FC）模式。首先在MIMO模式下发射一组正交信号，分别估计出收发端的时延差和相位差；然后雷达切换到 FC模式，发射一组相同波形，利用估计的相干参数分别对收发端的时延和相位作精确补偿，从而实现收发全相参。FC模式是DAFC雷达所独有的常态化模式，是MIMO雷达所不具备和无法实现的。

国外主要是美国林肯实验室对DAFC雷达技术做了大量研究[15]-，国内目前对该技术的研究尚属起步阶段，但是其潜在优势和应用前景已引起各大高校和研究所的关注[614]-。文献[5]定义了FC模式下的输出信噪比增益（output Signal to Noise Ratio gain, oSNRg）。文献[6-8]给出了部分线馈和空馈实验结果，并指出了关键技术及突破思路。文献[9,10]研究了时间和相位同步问题以及相位差跟踪技术。文献[11]首先建立了“多发多收”的一般结构，然后推导了时延差和相位差估计的克拉美-罗界（Cramer-Rao Bounds, CRB）闭式解，并基于CRB分析了相参处理性能。文献[12-14]将发射单脉冲拓展到多脉冲，研究了相干参数估计和相参处理性能与脉冲数的关系。文献[15]基于系统相位同步构建了DAFC雷达信号模型，分析了时延差估计和相参处理性能对相位同步误差的敏感性。文献[16]将峰值法（peak picking）和正交频分线性调频信号设计相结合，研究了高精度相干参数估计所需的信号设计要求。

目前对DAFC雷达的研究主要集中在信号模型构建、相干参数估计的CRB推导以及时间和相位同步系统设计，而对相干参数估计算法研究较少。相关法（cross-correlation）原理简单，便于工程实现，因此常用于DAFC雷达的相干参数估计。本文针对一般结构的DAFC雷达，研究基于相关法的相干参数估计及相参处理性能，重点分析相位差估计时存在的相位模糊问题，并给出一种易实现的解模糊方法。最后利用正交四相编码波形，通过数值实验验证结论的正确性和解模糊方法的有效性。

2 信号模型

由K个发射天线（T1, T2,… ,TK）和L个接收天线（R1,R2,… ,RL）组成的一般结构的分布式MIMO雷达，如图1所示。雷达发射一组正交信号，在接收端通过匹配滤波恢复每个发射信号分量。假设发射一组能量归一化的正交窄带信号为 sk（t）（k = 1,2,…,K）。经上变频，发射信号复包络可表示为，其中f为载频，为发射天

c线 Tk经上变频引入的初始相位。假设空间存在一个各向同性散射点目标，其确定性复散射系数为，则天线 Rl接收回波的低通等效式可表示为

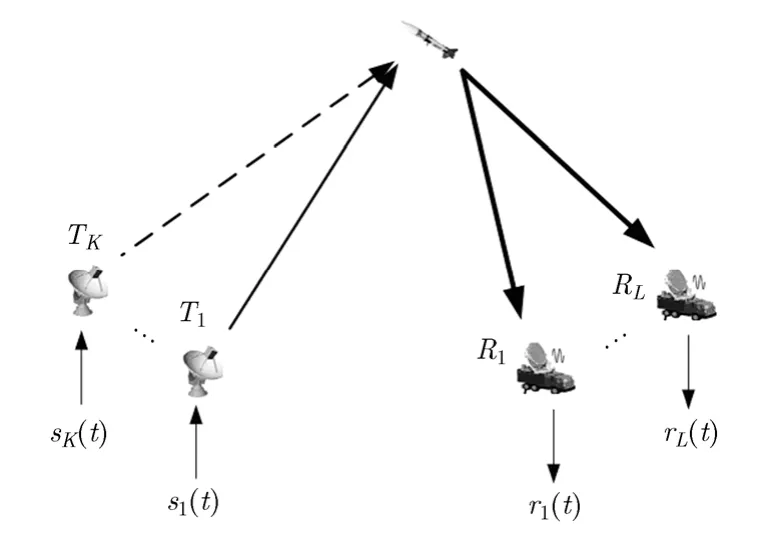
图1 一般结构的分布式MIMO雷达

3 相关法原理

将 rl（ t）分别通过K个匹配滤波器：（k = 1 ,2,…, K ,（.）*表示复共轭），假设发射波形理想正交，则匹配输出（不考虑噪声）可表示为

发射和接收相位差估计可分别表示为

4 相位差稳健估计

4.1 相位模糊分析

利用相位具有2π 周期性， Δ θt可改写为

k

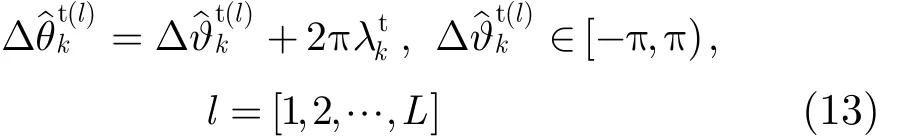
由于相位具有2π周期性，因此对于FC模式下的相位差补偿而言，与是等效的。为便于表述，记估计子为“直接加权平均（Directly Weighted Average, DWA）”。

首先给出周期估计误差（Periodic Estimation Error, PEE）的定义。假设待估计参数为ε，其估计值为εˆ，则εˆ关于周期Ω的PEE:εδˆ定义为显然≤Ω/2。Δ关于周期2π的PEE可表示为

k k位差真实值与估计值之间的相位模糊关系，是由估计误差导致的，例如噪声或波形非理想正交引起的估计误差。

关于周期2π的PEE可表示为

4.2 解相位模糊

则

图2 和之间的模糊关系

l0K ]）作为参考，则的ARE估计子可表示为

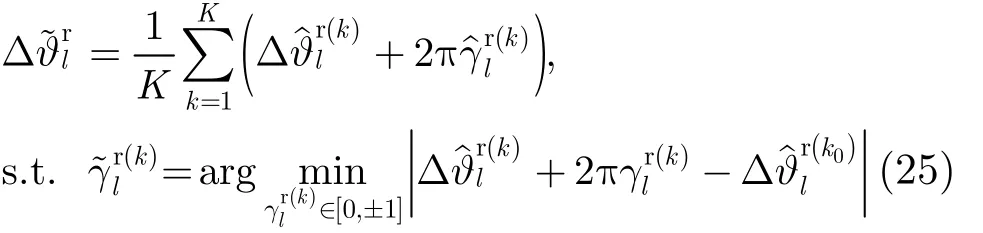
5 仿真及数据结果分析

DAFC雷达的收发天线配置为 L = K =2；载频fc= 1 GHz; MIMO模式下选用两组正交四相编码波形[8]，每组码含有128个子脉冲，每个子脉冲宽度为1 μs。目标到各收发天线的时延在（0,T/2）（T = 1 28 μs ）内随机选取；收发初始相位在[- π, π） 内均匀分布；噪声服从复白高斯过程，每个 S NRin取值点独立进行500次Monte-carlo实验。考虑以下两类目标模型。

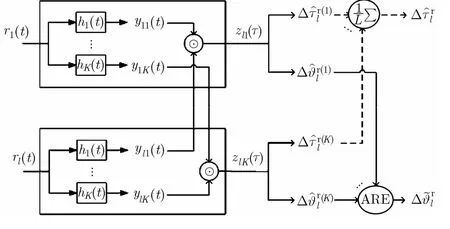
图4 和的稳健估计流程

单散射点（Single Scatterer, SS）目标模型：目标只包含1个散射点，其RCS为ξ= 1 。

主散射点（Dominant Scatterer, DS）目标模型：目标共包含 10个独立的散射点，其中一个主散射点，其RCS为ξ= 1 ；其余9个为辅散射点，RCS在区间[0 .05,0.15]内均匀分布。

实验1 时延差估计性能 针对两类目标模型，相关法估计收发时延差的 RMSE（Root Mean Squared Error）随 S NRin的变化曲线如图5所示。由图可知：对于 SS目标模型，接收时延差估计的RMSE随 S NRin增加逐渐逼近CRB[13]；由于发射波形非理想正交，发射时延差估计精度低于接收时延差；两者的 S NRin阈值（RMSE曲线斜率出现剧烈变化的 S NRin值）分别约等于18 dB和24 dB。相比SS目标模型，DS目标模型对应的发射或接收时延差的SNRin阈值更高。

实验2 估计子URE与ARE等价性验证 定义估计子 URE与 ARE的等价概率（Equivalence Ratio, ER）为：估计子URE与ARE等价的次数与实验总次数之比。针对两类目标模型，图6分别展示了接收和发射（等效）相位差对应的URE和ARE的ER随 S NRin的变化曲线。由图可知，对于两种目标模型，接收或发射对应的 ER随 S NRin增加逐渐趋于概率1。

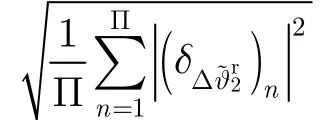
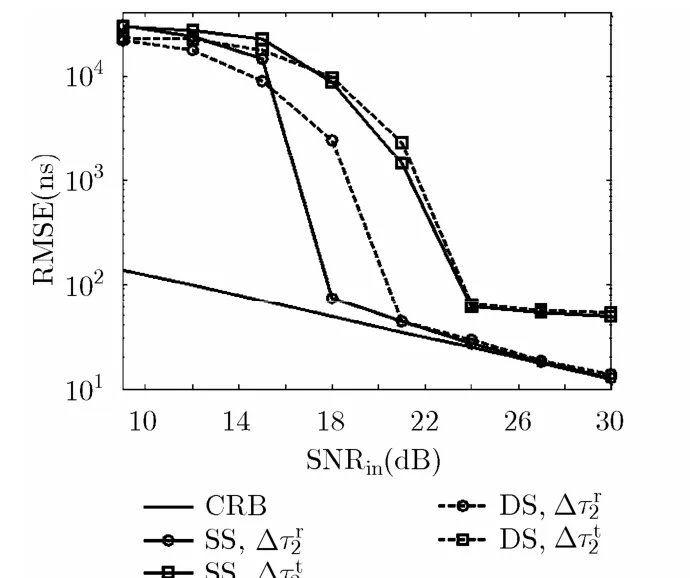
图5 时延差估计的RMSE随 S NR in 的变化曲线

（1）两类目标模型的实验结果类似；（2）由于DWA估计相位差时存在相位模糊，因此DWA估计失效；（3）URE或ARE对应的RMSE随 S NRin增加逐渐接近 CRB[13]，且 S NRin阈值约等于18 dB; （4）当SNRin不小于18 dB时，URE和 ARE对应的RMSE曲线完全重叠，由图6可知这是由于二者的ER等于1。

实验 4 相参处理性能 在 FC模式任选MIMO模式下一组码分信号作为发射波形。针对两类目标模型，实验获得3种估计子对应的oSNRg随SNRin变化曲线如图9所示。由图可知：（1）两类目标模型的实验结果类似；（2）由于估计子DWA缺乏稳健性，因此在 S NRin较高时，DAM对应的oSNRg无法达到理想上界; （3）URE和ARE对应的oSNRg曲线近似，这是由于二者的相位差估计精度近似；随着 S NRin逐渐增加，URE（或ARE）对应的oSNRg曲线接近理想上界; （4）尽管在低信噪比区域（S N Rin≤15 dB） URE较ARE的相位差估计精度更高（如图7或图8所示），但在 S NRin较低时 oSNRg主要受到时延差估计精度的影响，因此URE和ARE对应的oSNRg近似。

6 结束语

针对一般结构的DAFC雷达，研究了相关法的相干参数估计及相参性能。基于周期估计误差的定义，分析了估计相位差时的相位模糊问题，并提出了一种易实现的解相位模糊方法。仿真实验考虑了多种目标模型，利用正交多相编码波形作为发射信号，数值结果表明提出的解相位模糊方法是稳健有效的；由于发射波形非理想正交，接收相干参数的估计精度高于发射相干参数；在输入信噪比较高时，oSNRg接近理想上界2K L。为更好地指导工程应用，下一步将设计DAFC雷达的闭环信号处理框架，研究相参性能监控方法以及工作模式切换策略。

图6 URE和ARE的ER随 S NR in 的变化曲线

图7 的RMSE随 S NR 的变化曲线in

图8 的RMSE随 S NR 的变化曲线in

图9 oSNRg随 S NR in 的变化曲线

[1] Ahlgren G W. Next generation radar concept definition team final report[R]. MIT Lincoln Laboratory, 2003.

[2] Cuomo K M, Coutts S D, McHarg J C, et al.. Wideband aperture coherence processing for next generation radar（NexGen）[R]. MIT Lincoln Laboratory, 2004: 11-16.

[3] Coutts S D, Cuomo K M, McHarg J C, et al.. Distributed coherent aperture measurements for next generation BMD radar[C]. Fourth IEEE Workshop on Sensor Array and Multichannel Processing, Walthma, MA, USA, 2006:390-393.

[4] Brookner E. Phased-array and radar astounding breakthroughs an update[C]. IEEE Radar Conference,Boston, MA, USA, 2008,doi:10.1109/RADAR.2008.4720771.

[5] Fletcher A and Robey F. Performance bounds for adaptive coherence of sparse array radar[C]. 11th Conference Adaptive Sensors Array Processing, MIT Lincoln Laboratory,Lexington, MA, USA, 2003: 290-293.

[6] 鲁耀兵, 张履谦, 周荫清, 等. 分布式阵列相参合成雷达技术研究[J]. 系统工程与电子技术, 2013, 35（8）: 1657-1662.Lu Yao-bing, Zhang Lü-qian, Zhou Yin-qing, et al.. Study on distributed aperture coherence synthetic radar technology[J].Systems Engineering and Electronic, 2013, 35（8）: 1657-1662.

[7] 曹哲, 柴振海, 高宏卫, 等. 分布式阵列相参合成雷达技术研究与试验[J]. 现代防御技术, 2012, 40（4）: 1-11.Cao Zhe, Chai Zhen-hai, Gao Hong-wei, et al.. Technology and tests on distributed aperture coherence synthesizing radar[J]. Modern Defence Technology, 2012, 40（4）: 1-11.

[8] Gao Hong-wei, Cao Zhe, Wen Shu-liang, et al.. Study on distributed aperture coherence synthesizing radar with several experiment results[C]. Proceedings of the IEEE Radar Conference, Xi’an, China, 2011: 84-86.

[9] 曾涛, 殷丕磊, 杨小鹏, 等. 分布式全相参雷达系统时间与相位同步方案研究[J]. 雷达学报, 2013, 2（1）: 105-110.Zeng Tao, Yin Pi-lei, Yang Xiao-peng, et al.. Time and phase synchronization for distributed aperture coherent radar[J].Journal of Radars, 2013, 2（1）: 105-110.

[10] 殷丕磊, 杨小鹏, 曾涛. 分布式全相参雷达的相位差跟踪技术[J]. 信号处理, 2013, 29（3）: 313-318.Yin Pi-lei, Yang Xiao-peng, and Zeng Tao. Tracking technology of phase difference for distributed aperture radar[J]. Journal of Signal Processing, 2013, 29（3）: 313-318.

[11] Sun Pei-lin, Tang Jun, He Qian, et al.. Cramer-Rao bound of parameters estimation and coherence performance for next generation radar[J]. IET Radar, Sonar & Navigation, 2013,7（5）: 553-567.

[12] Tang Xiao-wei, Tang Jun, He Qian, et al.. Cramer-Rao bounds and coherence performance analysis for next generation radar with pulse trains[J]. Sensor, 2013, 13（4）:5347-5367.

[13] 宋靖, 张剑云, 郑志东, 等. 分布式全相参雷达相干参数估计性能[J]. 电子与信息学报, 2014, 36（8）: 1926-1931.Song Jing, Zhang Jian-yun, Zheng Zhi-dong, et al.. Coherent parameters estimation performance for distributed aperture coherent radar[J]. Journal of Electronics & Information Technology, 2014, 36（8）: 1926-1931.

[14] 宋靖, 张剑云. 分布式全相参雷达相参性能分析[J]. 电子与信息学报, 2015, 37（1）: 9-14.Song Jing and Zhang Jian-yun. Coherence performance analysis for distributed aperture coherent radar[J]. Journal of Electronics & Information Technology, 2015, 37（1）: 9-14.

[15] 宋靖, 张剑云, 代林, 等. 基于相位同步的分布式全相参雷达参数估计及相参性能[O L]. 中国科学: 信息科学,2015.http://info.scichina.com/sciF/CN/abstract/abstract 516987.shtml.Song Jing, Zhang Jian-yun, Dai Lin, et al.. Parameters estimation and coherence performance for distributed aperture coherent radar based on phase synchronization[OL].Scientia Sinica Informationis, 2015. http://info.scichina.com/sciF/CN/abstract/abstract 516987.shtml.

[16] 宋靖, 牛朝阳, 张剑云. 分布式全相参雷达 LFM 信号设计及性能分析[J]. 中国科学: 信息科学,doi:10.1360/N112014-00185.Song Jing, Niu Zhao-yang, and Zhang Jian-yun. OFD-LFM signal design and performance analysis for distributed aperture fully coherent radar[J]. Scientia Sinica Informationis,doi:10.1360/N112014-00185.