基于局部方差的MIMO频谱感知算法研究
贾 琼 李兵兵
1 引言
作为认知无线电网络[1]中关键的一个环节,频谱感知技术已经受到国内外学者的广泛关注。通过频谱感知技术,认知用户可以在不干扰主用户的前提下,发现频谱空洞,从而利用未被占用的频谱资源,大大提高频谱利用率。然而,在感知过程中往往存在虚警和漏检的情况,虚警的发生导致频谱利用率的降低,而漏检的发生则会给主用户带来干扰。另一方面,由于主用户的接入情况是随时变化的,所以必须保证在尽可能短的时间内完成感知。因此研究检测精度和感知效率较高,且易于实现的频谱感知算法具有非常重要的意义。
关于频谱感知算法,早期的研究一般针对单天线场景,具体有匹配滤波检测[2]、循环平稳特征检测[35]-和能量检测[68]-等。在完全已知主用户先验信息的情况下,匹配滤波是最佳检测器,然而实际应用中很难获得主用户的全部先验信息。循环平稳特征检测很好地克服了这一缺点,但其计算复杂度较高。能量检测由于原理简单便于实现,因而受到广泛的应用,但是能量检测的检测门限依赖于噪声功率,当完全已知噪声功率时,即理想的能量检测,性能最佳。但实际场合中噪声功率一般未知,进而在应用时采用估计的噪声功率值作为替代,然而估计的误差会导致检测性能的下降。为了解决这一问题,基于多天线的频谱感知技术被提出。其基本原理是,在主用户占用频段的情况下,认知用户接收端各个天线接收到的信号来源于同一个认知用户,因此彼此之间有着很强的相关性;而在频段空闲的情况下,由于接收到的是噪声,所以不存在相关性。利用这个相关结构,不需要已知噪声功率便可以设计出很好的检测器。Zeng等人[9]利用接收信号采样协方差矩阵的最大特征值与最小特征值比构造检验统计量,提出了最早的MME (Maximum-Minimum Eigenvalue)检测方法。在广义最大似然比检验(GLRT)的构架下,Lim 等人[10]提出了 AGM(Arithmetic to Geometric Mean)算法,该方法采用采样协方差矩阵特征值的算术平均和几何平均的比值作为检验统计量。随后Lopez-Valcarce等人[11]也在GLRT的基础上,提出了用采样协方差矩阵特征值的均值与最大值之比作为检验统计量的 Mean/Max检测方法。以上方法均可归结为特征值检测,虽然解决了能量检测需要估计噪声功率的问题,但是均需要进行复杂的特征值分解运算。此外,这些方法得以实现的前提均是基于认知用户各接收天线收到的噪声功率相等(均匀噪声)这一假设,而在实际应用中,由于天线的非标定等原因,认知用户接收端各天线处的噪声功率不相等(非均匀噪声),严重影响这些方法的检测性能。因此,必须研究更有效的算法来克服非均匀噪声造成的影响。文献[12]将采样协方差矩阵所有元素绝对值的累加和与对角线元素绝对值的累加和之比作为检验统计量,提出了 CAV (Covariance Absolute Value)算法;文献[13]则通过采样协方差矩阵的行列式构造检验统计量,提出了 VD (Volume-based Detection)算法。这些方法由于在建立检验模型时不受各天线噪声功率一致的约束,因而可以克服非均匀噪声的影响,但是要达到较高的检测性能,却需要比较大的采样点数。本文在采样协方差矩阵的基础上,定义了局部方差的概念,并以此构造检验统计量,提出了基于局部方差的MIMO频谱感知方法。该方法可以很有效地克服非均匀噪声带来的影响,而且由于本文方法利用了采样协方差矩阵元素的二阶统计特性,更充分地利用了信号间的相关结构,因此检测性能更高。此外,要达到同样的检测概率,局部方差法相比于其他方法所需的采样点数更小,因而具有更高的检测效率,可以广泛用于MIMO信号检测的实际应用中。
本文具体内容安排如下:第2节介绍均匀噪声和非均匀噪声下的MIMO频谱感知系统模型,并简要概括相关检测方法的基本原理;第3节分别从直观和理论的角度阐述局部方差频谱感知算法的基本原理,并且推导了算法理论门限;第4节为仿真与结果分析;第5节为结论。
2 系统模型
2.1 MIMO频谱感知模型
考虑一个主用户,一个认知用户的频谱感知系统,假设主用户和认知用户配置的天线数分别为M和N。则在第k个采样时刻认知用户接收端的接收信号可以表示为
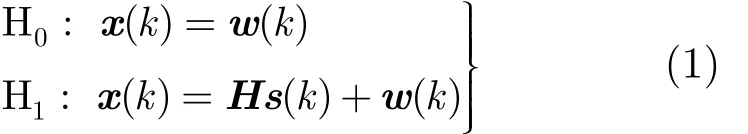

nwnσw(n = 1 ,2,… , N ),即认知用户不同天线处的噪声功率相等,则称为均匀噪声,否则为非均匀噪声。
2.2 均匀噪声下的MIMO频谱感知
在多天线场景中,利用采样协方差矩阵来表征信号之间的相关性,对于接收信号 X = [x ( 0),…,x(k ) ,…,x (K - 1)],其采样协方差矩阵定义为
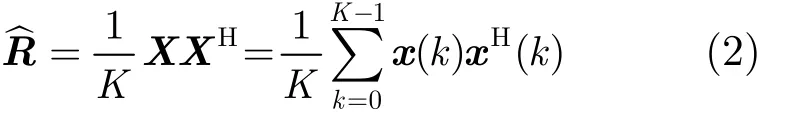
当采样点数足够大的时候有
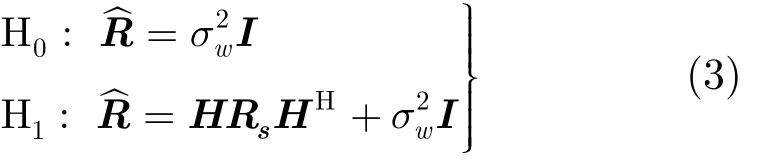
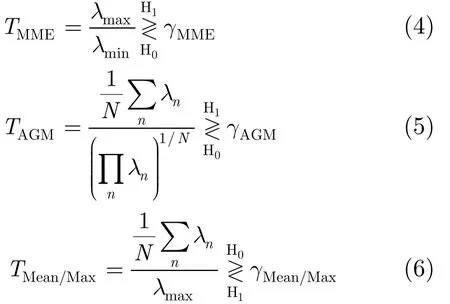
对于上述3种方法,其核心均是利用采样协方差矩阵︿R的特征值分别在0H和1H下特性的差异性从而构造相应的检验统计量做出判决。但是这一差异性存在的前提是要求认知用户接收端各天线处收到的噪声功率均相等,即认为噪声为均匀噪声。然而在实际应用中,由于天线非标定等原因,一般为非均匀噪声,因此会大大降低这些方法的检测性能,必须设计相应的检测算法来克服非均匀噪声造成的影响。
2.3 非均匀噪声下的MIMO频谱感知
在非均匀噪声环境下,采样协方差矩阵分别在两种假设下有式(7)形式:
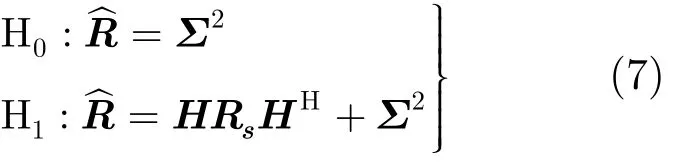
可见在假设0H下,采样协方差矩阵为对角矩阵,而在1H下,由于主用户信号的存在,接收端各天线间的信号具有相关性,因而采样协方差矩阵不再是对角矩阵。对于对角矩阵,矩阵所有元素的和等于对角元素的和,而对于非对角矩阵,则没有该特性。故CAV[12]检测方法的检验统计量构造为
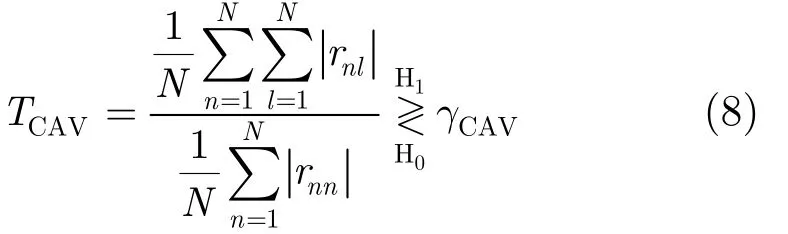
其中,nlr表示采样协方差矩阵第n行第l列的元素。
而VD[13]检测方法则通过利用︿R的行列式可以用来构造检验统计量,从而判决是否有主用户存在。
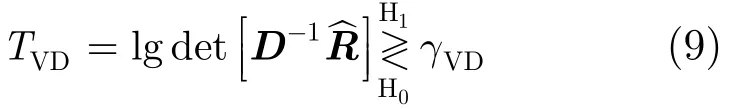
其中, D =diag[δ1,… ,δn, … ,δN],δn为的第n个行向量的范数。
上述两种方法,虽然可以在非均匀噪声场景下实现频谱感知,但是要达到较高的检测精度,需要的采样点数较多,因而感知效率不高。为了解决这一问题,本文提出了一种基于局部方差的MIMO频谱感知方法。
3 基于局部方差的MIMO频谱感知算法
对于目前已有的MIMO频谱感知算法,其核心思想均是利用采样协方差矩阵的相关结构分别在两种假设下的差异性,从而构造检验统计量,并与相应的门限比较,进而做出判决。而如何充分利用这种相关结构,是设计感知算法的关键。
根据前文所述,可知接收信号的采样协方差矩阵︿R在假设0H和1H分别为对角矩阵和非对角矩阵。用灰度值来表征矩阵每个元素的大小,可以得到非均匀噪声场景下,分别在0H和1H下的灰度示意图,如图1所示。在统计学中,方差用来衡量样本波动的大小。这里把一个矩阵的每个行向量看作一个样本,显然,在两种假设模型下,每个样本的方差有很大的差异。将所有样本方差的统计平均定义为矩阵的局部方差,则︿R的局部方差可以作为检验统计量来实现频谱感知。
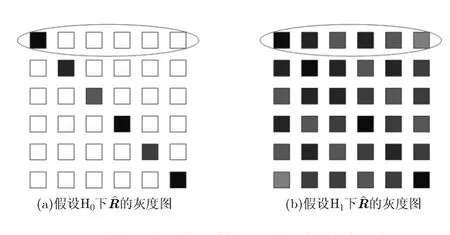
图1 非均匀噪声环境下采样协方差矩阵的灰度示意图
3.1 局部方差频谱感知算法
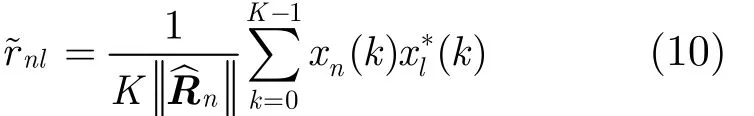
那么,矩阵~R的局部方差为
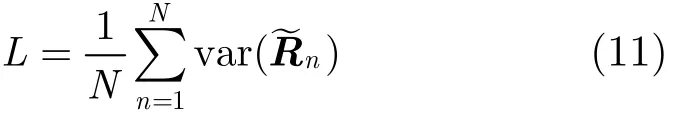
在假设1H下,由于主用户信号的存在使得认知用户各接收天线收到的信号之间具有较强的相关性,所以,采样协方差矩阵的局部方差会明显小于假设0H下只有噪声信号的情况。故而,通过与相应的门限作比较,便可以判决主用户是否存在。
因此,基于局部方差的MIMO频谱感知的判决准则为

3.2 判决门限的确定
由于实际应用中,主用户信号以及信道的先验信息通常未知,因此判决门限一般根据虚警概率来确定。根据式(12)中的判决准则,可得虚警概率为:Pf= p ( L < γ H0) 。可见,要确定判决门限,首先需要求得检验统计量L的概率分布。
将式(11)进行展开,可得
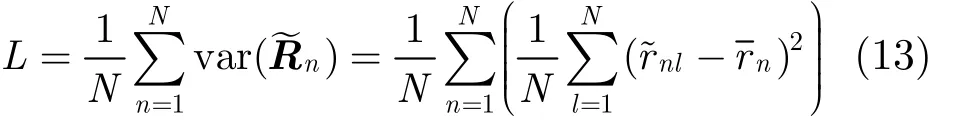
在假设 H0下,= 0 (l ≠ n),rn= ( 1/ N ) r~nn,因此,
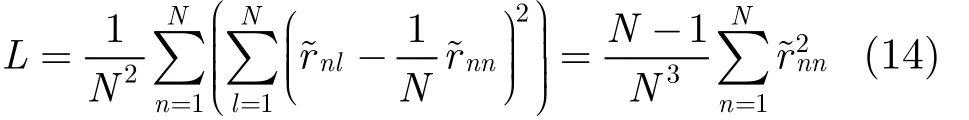
根据中心极限定理可知,nnr~ 服从高斯分布,又
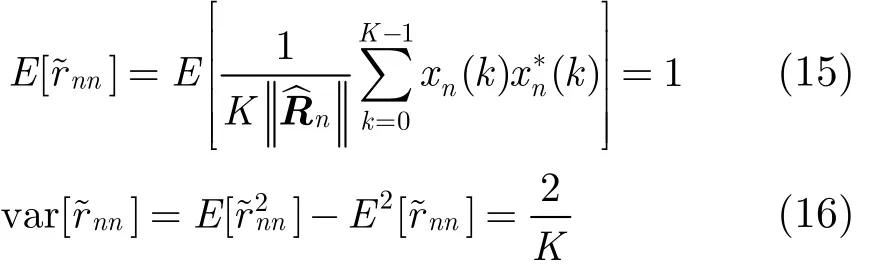
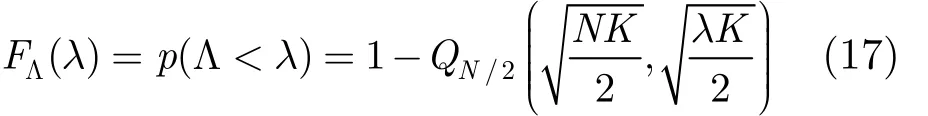
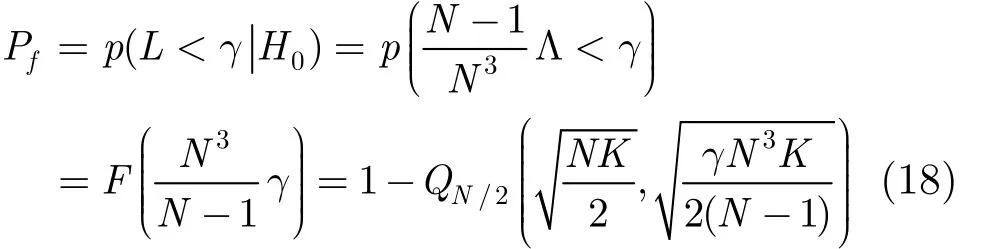
因此,可以计算虚警概率为故,对于一个给定的虚警概率指标fPη=,基于局部方差的频谱感知方法中的判决门限γ可以被确定为
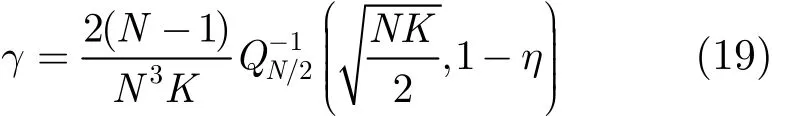
(1)初始化参数y,a,m以及搜索步长h,并赋初值 b = 0 ;
(2)计 算 z = Qm(a, b) (可 利 用 Matlab中marcumq函数求解);
(3)若z = y ,则停止搜索,转步骤(5);
(4)否则,令b = b + h ,转步骤(2);
4 仿真与结果分析
本节通过仿真,验证文中所提基于局部方差的MIMO频谱感知方法的有效性。从多个方面对局部方差检测方法和其他频谱感知方法的检测性能作比较;同时对不同噪声(均匀和非均匀)分别在各种检测算法中造成的影响作了相应的对比。
4.1 不同信道环境下各检测算法的性能对比
分别考察 MIMO AWGN信道和 MIMO Rayleigh信道环境下,当噪声为均匀噪声时各检测算法的检测性能。仿真中,假设主用户信号为QPSK信号,每组性能对比均由10000次蒙特卡罗仿真实验得到。
为了充分验证本文方法的有效性,对本文系统模型中提及的所有多天线检测方法均进行了相应的仿真,此外还考察了理想的能量检测和传统的利用噪声功率估计值的能量检测的检测性能作为对比。图2给出了在AWGN信道下,发送天线数M=1,接收天线数目和采样点数分别取不同数值时各检测器的ROC性能曲线,在该仿真中,信噪比SNR=-10 dB。从图2中可以看出,在接收天线数目非常小时,理想的能量检测为最佳检测,而文中提出的局部方差法,优于其他多天线频谱感知方法,接近最优。随着天线数目的增加,多天线带来的分集增益会使得各检测算法的性能均有所提升。但是由于能量检测中没有利用信号的空间相关性,所以随着天线数目的增加,局部方差法以及 CAV, VD算法等会逐渐优于能量检测。而局部方差法由于利用到了协方差矩阵的二阶统计特性,更加充分地利用了信号的相关结构,所以,相比于CAV, VD算法等,局部方差法所需的采样点数更少。
图3给出了MIMO Rayleigh信道下各检测器的检测性能对比图。文献[15]对MIMO Rayleigh信道已进行了充分的研究,并证明信道矩阵H(N×M维)服从零均值,协方差矩阵为Σ的复高斯分布,且Σ的元素满足
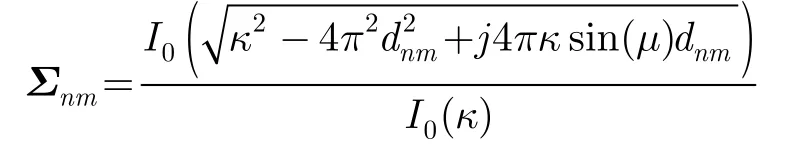
其中κ为到达角宽度,μ为到达角平均角度,dnm表示归一化天线间距。在该仿真中,取κ=80, μ=π / 2,相邻天线间的归一化距离为0.5,对比了当接收天线数目和采样点数分别取不同值时,各算法的检测性能。从结果中可以看出,天线数越大,局部方差法的优势越明显,而其他多天线频谱感知算法,在天线数目较大时,只有当采样点数足够大,才能获得较好的性能。
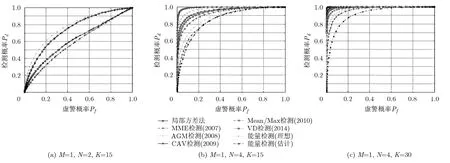
图2 MIMO AWGN信道下各检测器的ROC曲线对比图(SNR=-10 dB)
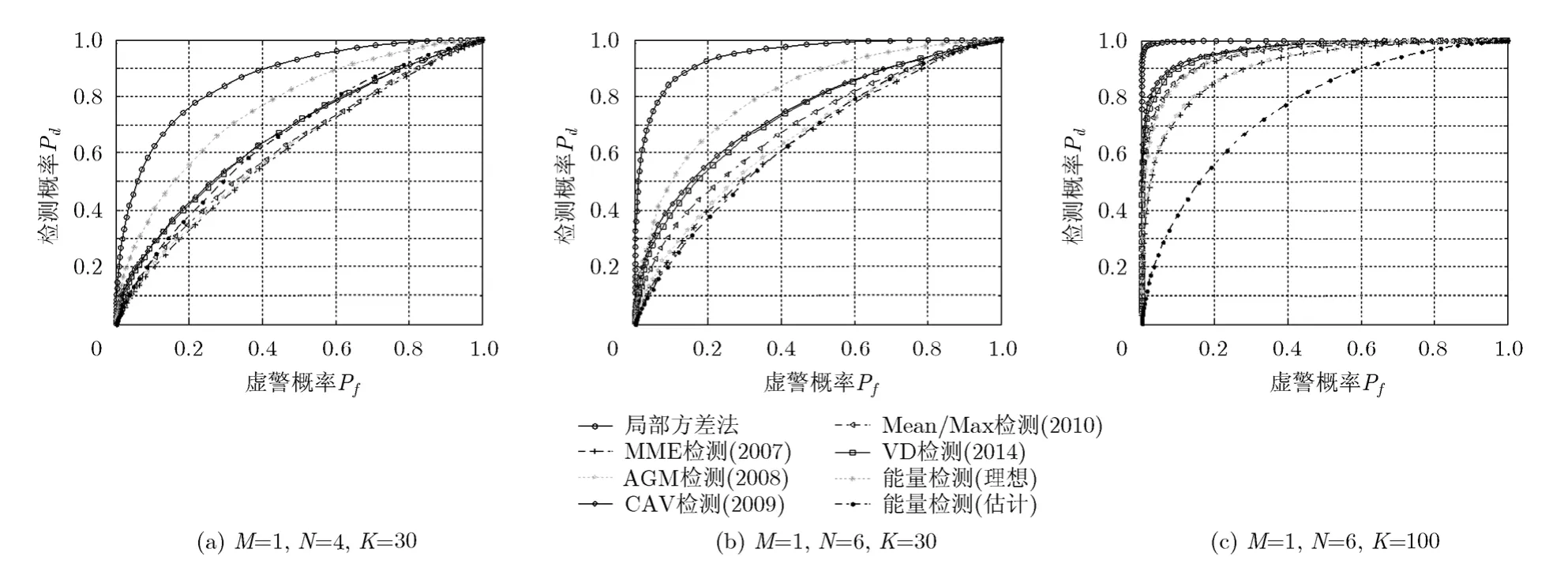
图3 MIMO Rayleigh信道下各检测器的ROC曲线对比图(SNR=-10 dB)
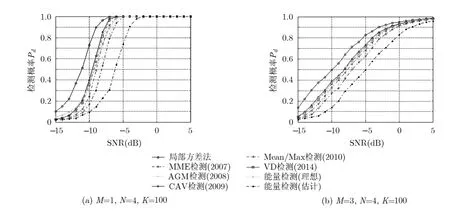
图4 MIMO Rayleigh信道下各检测器的检测概率随信噪比变化曲线对比图(Pf =0.01)
图4 则对比了MIMO Rayleigh信道下各检测器在发送天线取不同值时,检测概率随 SNR变化曲线。从结果中可以看出,在MIMO Rayleigh信道下,采样点数越大,各检测器的检测概率越高,然而当发送天线数增大时,各检测器的检测性能均会下降,这是由于在MIMO Rayleigh信道中,主用户各发射天线处的信号在传输过程中受到不同的信道衰落影响,从而导致认知用户各接收天线收到的信号之间的相关性变弱,因而降低了各检测器的检测性能。但是,无论发送天线数和采样点数的大小,局部方差法的检测概率均高于其他算法。
4.2 非均匀噪声对各个检测器的影响

图5 MIMO Rayleigh信道中各检测器在不同噪声作用下的ROC曲线对比图(M=1, N=4, K=30)
分别考虑均匀噪声和非均匀噪声两种情况,通过仿真比较各检测方法的检测性能。仿真中采用MIMO Rayleigh信道,设主用户为QPSK调制方式,发送天线数 M=1,接收天线数 N=4,采样点数K=30,信噪比SNR=-5 dB。对于非均匀噪声,天线端的噪声功率为[1,1.7,-0.7,-2] dB。从结果中可看出,MME, Mean/Max和AGM方法在非均匀噪声场景下,其检测性能甚至低于采用估计的能量检测。局部方差法,CAV方法和VD方法均可以克服非均匀噪声造成的影响,但是局部方差法的性能最佳。
5 结论
本文研究MIMO场景下的频谱感知问题,针对目前现有算法感知精度和效率均不够高的缺陷,提出了一种基于局部方差的MIMO频谱感知算法。该算法由于充分利用了采样协方差矩阵的相关结构,因而具有更高的检测精度,且所需采样点数更少,感知效率更高。此外,在算法的设计中,由于不需要已知主用户的先验信息,也无需对噪声功率进行估计,因此,文中提出的局部方差法可以广泛用于MIMO信号检测的实际应用中。
[1] Axell E, Leus G, Larsson E G, et al.. Spectrum sensing for cognitive radio: State-of-the-art and recent advances[J].IEEE Signal Processing Magazine, 2012, 29(3): 101-116.
[2] Yucek T and Arslan H. A survey of spectrum sensing algorithms for cognitive radio applications[J]. IEEE Communications Surveys & Tutorials, 2009, 11(1): 116-130.
[3] Ghozzi M, Marx F, Dohler M, et al.. Cyclostatilonariltybased test for detection of vacant frequency bands[C]. 1st IEEE International Conference on Cognitive Radio Oriented Wireless Networks and Communications, Mykonos Island,2006: 1-5.
[4] Zhu Y, Liu J, Feng Z, et al.. Sensing performance of efficient cyclostationary detector with multiple antennas in multipath fading and lognormal shadowing environments[J]. Journal of Communications and Networks, 2014, 16(2): 162-171.
[5] Sutton P D, Özgül B, and Doyle L E. Cyclostationary signatures for LTE advanced and beyond[J]. Physical Communication, 2014, 2014(10): 179-189.
[6] Srinu S and Sabat S L. Effective cooperative wideband sensing using energy detection under suspicious cognitive radio network[J]. Computers & Electrical Engineering, 2013,39(4): 1153-1163.
[7] Sofotasios P C, Rebeiz E, Zhang L, et al.. Energy detection based spectrum sensing over and extreme fading channels[J].IEEE Transactions on Vehicular Technology, 2013, 62(3):1031-1040.
[8] Gokceoglu A, Dikmese S, Valkama M, et al.. Energy detection under IQ imbalance with single-and multi-channel direct-conversion receiver: analysis and mitigation[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(3):411-424.
[9] Zeng Y and Liang Y C. Maximum-minimum eigenvalue detection for cognitive radio[C]. Proceedings. IEEE 18th International Symposium on Personal, Indoor and Mobile Radio Communications, Athens, 2007: 1-5.
[10] Lim T J, Zhang R, Liang Y C, et al.. GLRT-based spectrum sensing for cognitive radio[C]. IEEE Global Telecommunications Conference (GLOBECOM), New Orleans, LO, 2008: 1-5.
[11] López-Valcarce R, Vazquez-Vilar G, and Sala J.Multiantenna spectrum sensing for cognitive radio:overcoming noise uncertainty[C]. 2010 2nd IEEE International Workshop on Cognitive Information Processing(CIP), Elba, 2010: 310-315.
[12] Zeng Y and Liang Y C. Spectrum-sensing algorithms for cognitive radio based on statistical covariances[J]. IEEE Transactions on Vehicular Technology, 2009, 58(4):1804-1815.
[13] Huang L, So H C, and Qian C. Volume-based method for spectrum sensing[J]. Digital Signal Processing, 2014, 2014(28):48-56.
[14] John G Proakis. Digital Communications, Fifth Edition [M].New York, McGraw-Hill, 2009: 46-48.
[15] Abdi A and Kaveh M. A space-time correlation model for multielement antenna systems in mobile fading channels[J].IEEE Journal on Selected Areas in Communications, 2002,20(3): 550-560.

