单载波宽带MIMO系统广义近似消息传递Turbo频域均衡

王行业 王忠勇 李 塑 张传宗 王 玮

1 引言

多输入多输出（MIMO）无线系统可以实现很高的频谱效率，具有稳健的对抗信道衰落的性能，已成为下一代无线通信系统的关键技术之一。抑制符号间干扰（Inter-Symbol Interference, ISI）和共天线干扰（Co-Antenna Interference, CAI）并利用信道固有的频率分集和空间分集实现宽带 MIMO信道的理论优势，历来都是接收机设计中所要考虑的关键问题。

基于最大后验概率（Maximum A posteriori Probability, MAP）软输入软输出均衡器和MAP软输入软输出解码器之间外部软信息迭代交换的Turbo迭代均衡技术[1]，能同时有效克服宽带MIMO系统中的ISI和CAI，完全获得接收分集增益，实现最优的联合均衡和解码性能[2]。然而，由于MAP软输入软输出均衡器的计算复杂度随信道ISI长度、调制信号星座图大小和发射天线数增加呈指数形式增长，使其难以在实际系统中应用。所以，低复杂度近最优的软输入软输出均衡算法一直是接收机设计的研究热点[311]-。其中文献[3]对单天线系统提出了基于线性最小均方误差（Linear Minimum Mean Squared Error, LMMSE）的软输入软输出时域均衡算法，实现了良好的性能与复杂度折中。文献[4]将文献[3]的方法推广到宽带MIMO信道，提出了基于LMMSE准则的软输入软输出 MIMO频域均衡算法，以微弱的性能损失进一步降低了算法复杂度。文献[5]对文献[3]的结果给出了一种简洁的表示方法。文献[6]利用联合高斯法提出了不同信道条件下适合于低阶调制信号的外部似然比计算方法。文献[7]和文献[8]分别针对空间相关信道和功率失衡多用户信道提出了用户分群和连续干扰抵消的 LMMSE Turbo频域均衡方法。文献[9]针对比特交织编码调制（Bit-Interleaved Coded Modulation, BICM）空间复用宽带 MIMO传输系统提出了一个通用的LMMSE意义下最优的块迭代频域判决反馈均衡框架，并对渐进性能进行了分析。它们的共同特点是均采用LMMSE准则来推导软输入软输出均衡器。但误码率最优的是 MAP准则下的检测器。因此，文献[10]针对单输入单输出系统，采用广义近似消息传递算法（Generalized Approximate Message Passing, GAMP）[11,12]提出了一种新的Turbo频域均衡方法。该频域均衡器（Frequency Domain Equalizer, FDE）对正交相移键控（Quadrature Phase Shift Keying, QPSK）信号，在严重频率选择性信道上达到了接近加性高斯白噪声（Additive White Gaussian Noise, AWGN）信道上的性能边界。许多文献采用因子图（Factor Graph, FG）消息传递[13]方法研究MIMO软输入软输出均衡问题，并获得了良好的性能与计算复杂度折中。但其主要集中在时域均衡[14]和 MIMO 正交频分复用（Orthogonal Frequency Division Multiplexing,OFDM）系统[15]的研究中。

为进一步提升MIMO FDE的性能，本文基于GAMP算法[11,12]，设计一种新的软输入软输出MIMO FDE，该算法可以认为是文献[10]的方法在MIMO系统中的推广。GAMP算法是一种适用于密集联接有环因子图的近似推理算法，它采用一系列标量估计来近似实现线性混合估计问题中的向量估计[11,12]。所提出的GAMP MIMO均衡算法既保留了经典输入软输出 FDE由快速傅里叶变换（Fast Fourier Transformation, FFT）和反变换（Inverse Fast Fourier Transformation, IFFT）带来的低复杂度优势，同时又规避了LMMSE输入软输出MIMO均衡中的MIMO信道矩阵求逆的问题。另外，为了便于输入软输出MIMO频域均衡器的推导，该文采用向量矩阵方式描述文献[11,12]中的标量形式GAMP算法。

本文结构安排如下：第2节给出了编码单载波空间复用宽带MIMO系统模型。第3节基于向量矩阵GAMP算法，推导了一种新的软入软出MIMO频域均衡器。第4节通过计算机仿真分析了所提接收机的性能。第5节总结全文。

本文符号说明： （A ）diag表示由矩阵A的对角线元素所构成的对角矩阵，⊗表示矩阵之间的Kronecker乘积，x ～CN （ x, vx） 表示随机向量x服从均值为x协方差矩阵为 vx的复高斯分布。

2 系统模型

考虑一个 NT发射 NR接收的单载波（Single Carrier, SC）循环前缀（Cyclic Prefix, CP）空间复用MIMO系统。每根天线独自对长度为 Nb的信息比特流进行编码，编码比特经随机交织后产生长度为Nc的比特流 ，再通过正交幅度调制（Quadrature Amplitude Modulation, QAM）符号格雷映射，形成长度为N的符号块，其中为第 n 天线上的符号块，txn,nt∈S,S为QAM星座图，S中每一星座点对应Q个编码比特。对NT个并行符号块添加CP后，由NT根发射天线以相同的载波频率送入无线信道。假设每对收发天线之间的信道为瑞利块衰落，在每个符号块内保持不变，在不同块之间随机变化。信道脉冲响应长度均为 L。忽略收发天线之间的空间相关性。假设CP的长度大于L，天线收发完全同步。在接收端去掉CP后，接收天线的频域接收信号向量y可表示为[6,9]

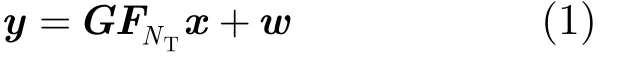
其中为频率点n上NT根发射天线和NR根接收天线收之间的频域信道矩阵。令 Heff=GFNT，式（1）又可表示为

对于式（3）的接收信号模型和发射机所采用的编码器结构，误码率（Bit Error Rat, BER）最优的MAP接收机[1,14]为

p（ bnt,nb|y）为给定y时 bnt,nb的后验概率。

3 基于GAMP算法的软输入软输出MIMO频域均衡

3.1 GAMP算法基础

与采用高斯消息近似以降低计算复杂度获得的传统的软输入软输出FDE相比，GAMP算法是依据一定的数学理论所推导出的一种近似和积算法（Sum- Product Algorithm, SPA）[10,11]。按照 GAMP算法，模型式（3）表示的检测问题，可以看成是AWGN环境中的effH 为线性混合矩阵的线性混合估计问题。为便于充分利用effH 中的特殊结构，设计高效的软输入软输出 FDE，本文将文献[11]中的标量GAMP算法归纳为如表1所示的矩阵向量形式算法，其中α为归一化常数。

3.2 基于GAMP算法的MIMO迭代频域均衡

考虑频域模型式（3），为便于表示，在以下推导中略去表1中GAMP算法中的迭代指标，并用effH代替H。注意到表1算法中pV,sV和rV 均为对角矩阵。

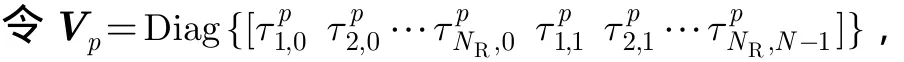
有

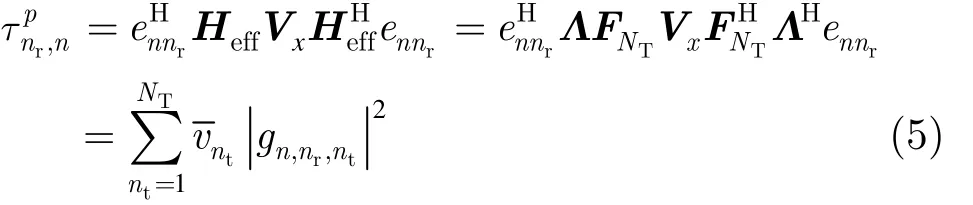
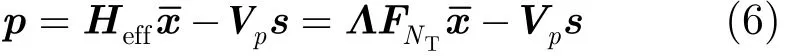
令

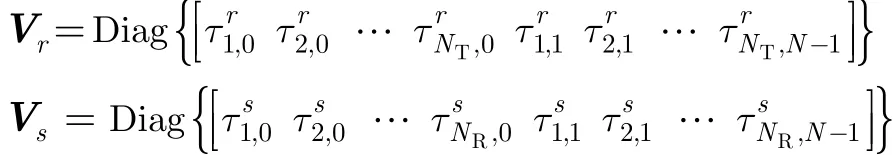
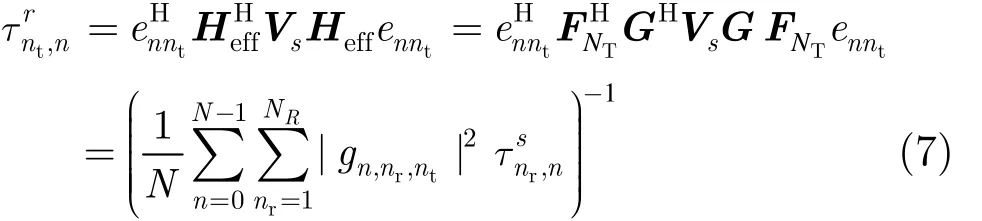
表1 矩阵向量形式GAMP算法

基于频域模型式（3）推导的 GAMP软输入软输出MIMO FDE如表2所示。

表2中 cnt,n,q表示发射天线nt传输的第n个信道符号中包含的第q个编码比特，p （ cnt,n,q）为译码器向均衡器反馈的关于的先验概率。为均衡器输出的关于的外部对数似然比（Log-Likelihood Ratios, LLRs）。注意，如果软输入软输出MIMO FDE内部不包含迭代，即 Imax=1时，利用上一次Turbo迭代中GAMP算法输出的 sImax为本次迭代提供s的初值。

3.3 计算复杂度分析

以算法所需要的浮点运算次数（FLOating-Point operations, FLOPs）来评价以上软输入软输出MIMO FDE的计算复杂度。一次实数乘法和一次实数加法均需要 1FLOPs。将和）}的计算开销归入译码器部分，在均衡器计算复杂度分析中不再考虑。对于表2描述的基于GAMP算法的软输入软输出MIMO FDE，预处理步和{p（ x =α）}的计算分别需要3NN nt,n qRFLOPs和（Q-1）FLOPs，迭代步中xi和的计算共需要NN（19×2Q+2）FLOPs，其中指T数运算exp（.）采用查表实现，一次查表操作需要6FLOPs。假设采用基-2 FFT进行N点FFT，需要（5N l og2（N ） - 1 0N + 1 6）FLOPs，则计算 ri和共需 要 （ （20NR+ 10log2（N ） - 18）N NT+ 7 N NR+ 32NT）FLOPs。 NR× NR维共轭对称复数矩阵的求逆大约需要FLOPs，对于传统软输入软输出MIMO FDE[5,6]，大约共需要FLOPs。在 NT= NR, Imax=1时，以上两种软输入软输出MIMO FDE的每Turbo迭代每符号计算复杂度，即正规化计算复杂度如表3所示。

表2 基于GAMP算法的软输入软输出MIMO FDE

表3 不同软输入软输出MIMO FDE的正规化计算复杂度

当S =16,N = 256,NT=NR,Imax= 1 时，这两种软输入软输出MIMO FDE的正规化计算复杂度随发射天线数 NT的变化如图1所示，其中以“conv”表示传统MIMO频域均衡方案，而“GAMP”表示基于SP-GAMP算法的软MIMO FDE方案。从图3可以看出， NT较小（NT＜ 4 ）时，基于GAMP算法的软输入软输出MIMO FDE的计算复杂度略高于传统的方法，这主要是由前者需要额外估计发送符号置信所造成的。但随 NT的增加，发送符号置信的额外估计所产生的计算开销，在整个均衡器计算开销中的比重越来越低，此时GAMP均衡方法无需矩阵求逆的优势越来越明显，所以其总体计算复杂度增长缓慢。而传统的MIMO FDE由于涉及矩阵求逆，导致了计算复杂度的快速增长。当 NT≥ 4 ，基于GAMP算法的软输入软输出MIMO FDE的计算复杂度明显低于传统的方法。

4 仿真结果

为研究本文所提出的软输入软输出MIMO FDE的性能，本文分别仿真了2×2和4×4的编码MIMO通信系统的误码率性能，在两种天线配置中，各发射天线均采用速率为1/2、生成多项式为（23,35）8的卷积编码器进行独立编码，并使用独立随机交织器对编码比特进行交织，交织的后编码比特又被映射为16QAM信道符号。每一个码字对应一个长度为256的信道数据块，添加CP后通过频率选择性MIMO无线信道传输。信道多径数分别设定为6和4，且不同发射天线和接收天线之间的信道参数服从均匀功率谱相互独立的瑞利分布。信道在每个数据块内保持不变，在各个数据块之间则是互不相关的。接收端已得到了信道参数和加性复高斯白噪声方差的准确估计。仿真发现增加软输入软输出MIMO FDE内部迭代不会明显改善检测性能，所以本文算法中设定max=1I 。为了比较方便，匹配滤波界（Matched Filter Bound，MFB），均以“MFB”为标示，绘制在同一张图上。

图2和图3分别给出了两种MIMO系统中本文所提出的基于GAMP算法的软输入软输出MIMO FDE与传统软输入软输出MIMO FDE[5,6]的BER性能比较。其中以“conv 1st”“conv 6th”和“conv 10th”分别表示传统MIMO频域均衡方案经过第1次、第6次和第10次迭代后的检测性能，以“GAMP 1st”“GAMP 6th”和“GAMP 10th” 分别表示基于SP-GAMP算法的软输入软输出MIMO FDE方案经过第1次、第6次和第10次迭代后的检测性能。从图中可以看出，在这两种系统配置中，本文算法均获得了显著的迭代增益。尽管本文检测算法初次迭代明显比传统算法差，但经过6次迭代后，本文检测算法的性能在整个信噪比范围内均优于传统算法10次迭代。所以新方案可以较少迭代次数满足特定的BER性能要求，从而降低联合均衡和解码延迟，在对解码延迟要求严格的场合具有较好的实用性。另外，由图2和图3可看出，基于GAMP算法的MIMO Turbo频域均衡方法经过10次迭代，两种MIMO天线配置都能达到逼近MFB的性能，尤其是4×4宽带MIMO场景下，在大于7.5 dB的比特信噪比范围内，GAMP MIMO Turbo频域均衡的性能与MFB几乎是重合的。在 B ER = 1 0-4时，文中算法在两种MIMO配置中相对于传统算法分别有约1.35 dB和0.7 dB性能优势，获得了更好的性能与计算复杂性折中。

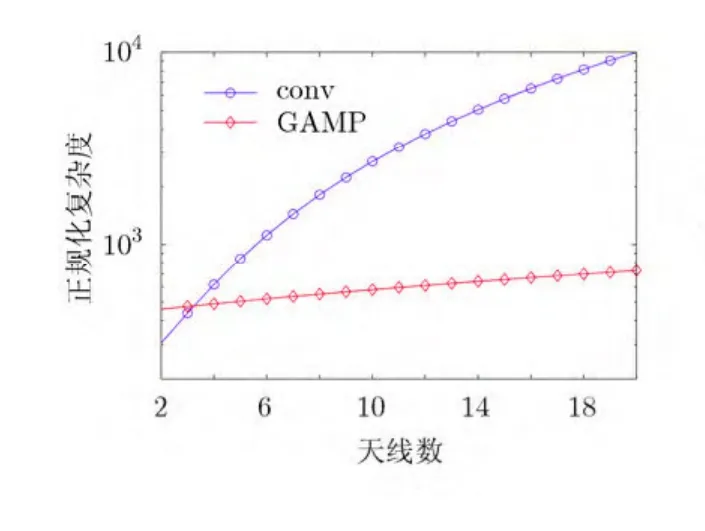
图1 正规化计算复杂度随天线数的变化

图2 2×2 MIMO系统接收机误码率性能

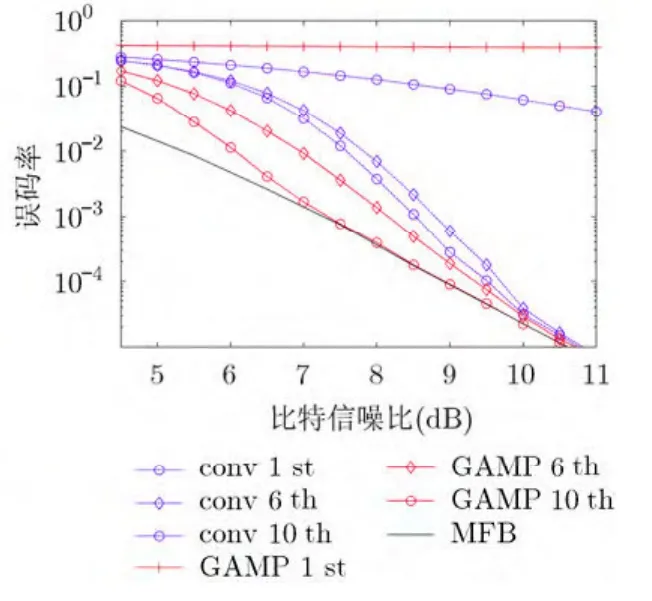
图3 4×4 MIMO系统接收机误码率性能

5 结束语

本文提出了向量形式的GAMP算法，使GAMP算法在实际应用中更便捷。在此基础上，提出了一种新型的高阶调制软输入软输出MIMO FDE接收机。由于GAMP算法从理论上考虑了信道符号的本质离散性，所以，相对于直接将离散符号按高斯分布处理的LMMSE软输入软输出 MIMO FDE,GAMP软输入软输出MIMO FDE能够产生更好的信道符号置信，给解码器提供更可靠的外部比特LLRs，进而获得了更好的联合检测与译码性能。此外，由于GAMP算法只涉及标量运算，使得在Turbo迭代应用中既保持了由于FFT所产生的计算优势又不涉及传统LMMSE软输入软输出MIMO FDE中的矩阵求逆问题，尤其适合大规模MIMO系统应用。

[1] Douillard C, Picart A, Didier P, et al.. Iterative correction of intersymbol interference: Turbo equalization[J]. European Transactions on Telecommunications, 1995, 6（5）: 507-511.

[2] Etzlinger B, Haselmayr W, and Springer A. Equalization algorithms for MIMO communication systems based on factor graphs[C]. Proceedings of the IEEE International Conference on Communications, Kyoto, Japan, 2011: 1-5.

[3] Tüchler M, Singer A C, and Koetter R. Minimum mean squared error equalization using a priori information[J]. IEEE Transactions on Signal Processing, 2002, 50（3）: 673-683.

[4] Yee M S, Sandell M, and Sun Y. Comparison study of single-carrier and multi-carrier modulation using iterative based receiver for MIMO system[C]. Proceedings of the IEEE Vehicular Technology Conference, Milan, Italy, 2004:1275-1279.

[5] Guo Q and Huang D. A concise representation for the soft-in soft-out LMMSE detector[J]. IEEE Communication Letters,2011, 15（5）: 566-568.

[6] Yuan X, Guo Q, Wang X, et al.. Evolution analysis of low-cost iterative equalization in coded linear systems with cyclic prefixes[J]. IEEE Journal on Selected Areas in Communications, 2008, 26（2）: 301-310.

[7] Grossmann M and Schneider C. Groupwise frequency domain multiuser MMSE turbo equalization for single carrier block transmission over spatially correlated channels[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5（8）:1548-1562.

[8] Zhang J and Zheng Y R. Joint frequency-domain multiuser turbo equalization with successive interference cancellation for doubly-selective fading Channels[J]. Wireless Personal Communications, 2013, 68（4）: 1317-1330.

[9] Guvensen G and Yilmaz A. A general framework for optimum iterative blockwise equalization of single carrier MIMO systems and asymptotic performance analysis[J].IEEE Transactions on Communications, 2013, 61（2）:606-619.

[10] Guo Q , Huang D, Nordholm, et al.. Iterative frequency domain equalization with generalized approximate message passing[J]. IEEE Signal Processing Letters, 2013, 20（6）:559-562.

[11] Rangan S. Generalized approximate message passing for estimation with random linear mixing[OL]. http://arxiv.org/abs/1010.5141v1.2010.

[12] Rangan S. Generalized approximate message passing for estimation with random linear mixing[C]. IEEE International Symposium on Information Theory Proceedings （ISIT）, St.Petersburg, Russia, 2011: 2168-2172.

[13] Kschischang F R, Frey B J, and Loeliger H A. Factor graphs and the sum-product algorithm[J]. IEEE Transactions on Information Theory, 2001, 47（2）: 498-519.

[14] Haselmayr W, Etzlinger B, and Springer A. Factorgraph-based soft-input soft-output detection for frequencyselective MIMO channels[J]. IEEE Communication Letters,2012, 16（10）: 1624-1627.

[15] Novak C, Matz G, and Hlawatsch F. IDMA for the multiuser MIMO-OFDM uplink: a factor graph framework for joint data detection and channel estimation[J]. IEEE Transactions on Signal Processing, 2013, 61（16）: 4051-4066.