掺杂硫化铅体系的电子性质研究
刘 鹏,李 炜 ,马娟娟
(华南师范大学物理与电信工程学院,量子信息技术实验室,广州510006)
自20 世纪50年代以来,铅硫族化合物PbX(X=S、Se、Te)及其合金已经被广泛地研究,特别是PbTe 作为热电材料[1]. 相比Ⅱ-Ⅵ和Ⅲ-Ⅴ族闪锌矿型半导体,这些窄隙Ⅳ-Ⅵ族半导体具有特殊的电子和结构性质,具有广泛应用前景[2]. 位于Pb价带较高能级的s 电子与阴离子p 电子之间的相互作用决定了其具有独特的电子性质[2],PbS、PbSe和PbSb 等铅硫族化合物被广泛研究[3-6].研究方法除了实验研究(如PbS[7-9])还有理论计算(如掺杂多种杂质PbSe[10]和PbTe[1]等).铅硫族化合物除了其在热电材料领域的应用以外,被广泛应用于红外二极管[11]、光电子[12]和基于PbSe/PbEuTe的红外量子点激光器[13]等.目前,相对于PbSe 和PbTe,掺杂PbS 材料关于电子和光学性质方面的研究较少. 基于密度泛函理论和广义梯度近似,本文采用第一性原理计算研究了多种杂质(Cd、Sn、Sb)掺杂的岩盐结构PbS 的电子性质.
1 计算方法与模型
1.1 计算方法
基于密度泛函理论,结合广义梯度近似(Generalized Gradient Approximation,GGA)交换关联中的PBE(Perdew-Burke-Ernzerhof)形式,采用Castep(Cambridge serial total energy package)程序[14-15]进行第一性原理能带结构的计算. 电子波函数采用平面波基组展开,其截止能设为400 eV,迭代过程中收敛精度设为1.0 ×10-6eV/atom,而且原子间的相互作用收敛标准为0.1 eV/nm. 晶体结构采用BFGS (Broyden Fletcher Goldfarb Shanno)算法进行几何优化;计算采用的掺杂体系是64 原子总数的2 ×2 ×2 岩盐结构PbS 立方超胞,原晶胞尺寸为:a =b =c =0.593 4 nm,晶胞角度均为90°,用2个掺杂原子替换超胞中的Pb 原子. 在布里渊区的积分计算使用Monkhorst-Pack 方案[16],选择k 网格点为4 ×4 ×4,选取倒易空间和超软赝势参与计算电子结构. 在计算中首先考虑了自旋轨道耦合,发现对于受主类型掺杂样品的杂质能态,自旋轨道耦合对它们的能级位置并无显著影响,这与文献[10]的结论一致. 因此,本文暂不考虑自旋轨道耦合的影响.
采用密集取样的布里渊区,以得到有良好收敛性能的基组,这对于光学性质的计算是必要步骤[17],所以使用一个规则的6 ×6 ×6 网格. 当所有能带结构都被自适应地计算后,由能带间的跃迁可得到频率相关的介电函数ε(ω)[4]. 介电函数的虚部Im[ε(ω)]=ε2(ω)采用Ambroch-Draxl 和Abt 的定义:
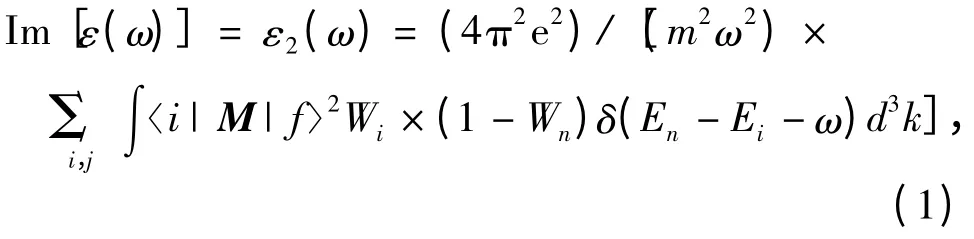
式中,M 是偶极子矩阵,i 和n 分别是初始态和最终态,Wi是第i 态的费米分布函数,而且Ei是在第i态下的电子能级. 从介电函数的虚部可推导出它的实部Re[ε(ω)]=ε1(ω)采用Kramers-Kronig 相关等式:
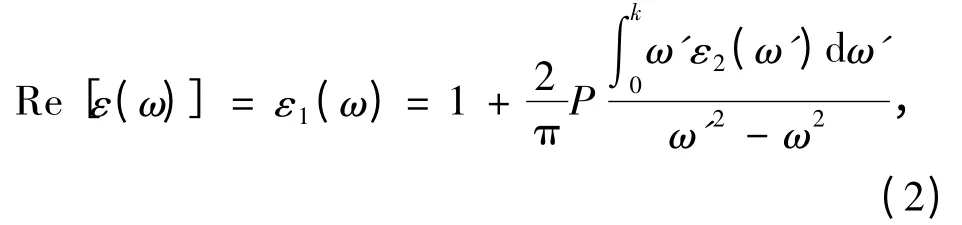
式中,P 代表积分的主值中性原子.
1.2 晶体模型
对于平衡掺杂浓度的计算,在所有掺杂配置下,其缺陷态和杂质的形成能可从相应的总能量中直接推出[18].对于每种杂质,其原子掺杂位置既有规律又是随机的[19]. 图1 中,基于晶胞原子在空间上的对称性及其随距离上的不同性,在恒定掺杂浓度(6.25%)下,首先考虑7 种不同配置的替换掺杂模型,然后通过形成能的计算,得到掺杂配置中最稳定的结构.
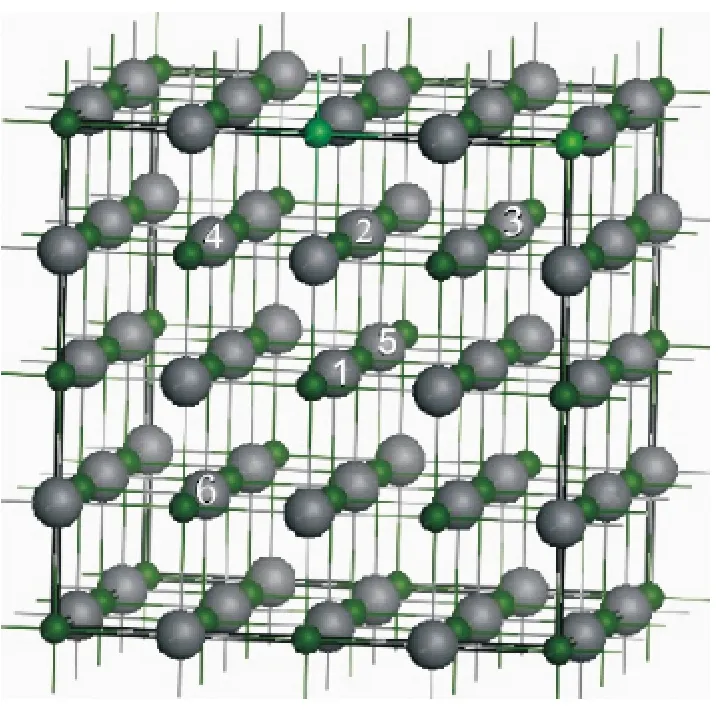
图1 PbS 的2 ×2 ×2 超胞掺杂模型Figure 1 2 ×2 ×2 supercell model of the doped-PbS
对于形成能的计算准则,采用文献[20]中被广泛解释的公式. 因此定义相关形式:
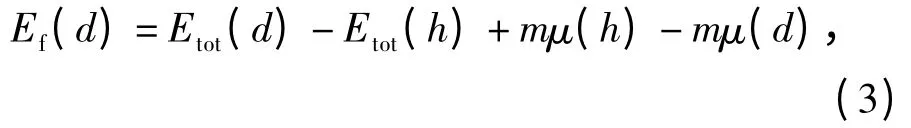
式中,Etot(d)是包含杂质d(d 为Cd、Sn 和Sb)的超晶胞总能,Etot(h)是未掺杂的超晶胞总能,这里代表h=Pb 没有被替换,同时m 表示被掺杂的原子数.μ(h)和μ(d)分别表示单个Pb 原子和单个杂质d原子的化学势[21]. 在3 种掺杂中,以Cd 掺杂PbS的样本为例计算形成能,得到7 种不同配置模型(图1)的形成能:Ef(4,6)=7.390 7 eV,Ef(1,2)=7.339 7 eV,Ef(1,3)=7.338 9 eV,Ef(1,4)=7.339 9 eV,Ef(1,5)=7.383 7 eV,Ef(3,4)=7.379 1 eV,Ef(3,6)=7.358 7 eV. Ef(1,3)的形成能最低为7.338 9 eV,从形成能的角度来说,最低的杂质形成能意味着最稳定的掺杂结构[22]. 因此,位置1 和位置3 为最佳掺杂位置. 同理确定Sn 和Sb 掺杂的最佳位置1 和最佳位置3,以得到恒定杂质浓度(6.25%)下电子和光学性质的特性.
2 结果与讨论
2.1 掺杂PbS 的电子结构
铅硫族化合物PbX(X =S、Se 和Te)的电子结构已经有了广泛研究[3-6]. 本文计算得到未掺杂PbS 超胞的带隙值为0.446 0 eV,与文献[23]中采用GGA 方法得到的带隙值一致;也符合其他文献[2,7-9,24]得 出 的 实 验 值 和 计 算 值(0.29~0.45 eV). 而且,其能带结构和分波态密度总体上也与文献[2]、[23]、[25]相似. 然后,在图2~图4 分别计算得到PbS:Cd、PbS:Sn 和PbS:Sb 样本的能带结构. 计算得到的PbS:Sn 样本能带结构和PbSe:Sn[10]类似;其能带结构和态密度也与PbTe[6]大体上一致. 计算得到的能隙值Eg=0.426 0 eV 和Eg=0.382 0 eV 分别对应于PbS:Cd 和PbS:Sn 掺杂样本.由于Cd 和Sn 原子与Pb 原子是等价的,所以前两者的替换掺杂不会产生空穴或者自由电子;其价带顶附近的能级和未掺杂的PbS 超胞价带顶附近的能级类似.因此,在后面的分析中,主要讨论其价带顶上面部分的计算能带结构. 图2B 给出了PbS:Cd样本的分波态密度和总态密度计算结果,容易区分为费米能级Ef下的3个区域,分别对应图2A 中第1 束靠近Ef的区域以及其他2 束偏很低能级的区域.从图中约1.4 eV 附近沿着F-Z-B-Q 波矢路径出现扁平能带,这些扁平能带主要和Cd -s 和Pb-p 轨道有关,S-p 轨道也有少量参与.
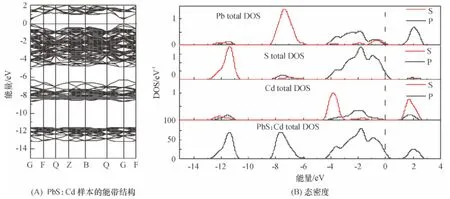
图2 PbS:Cd 样本的能带结构和态密度Figure 2 Band structures and density of states of PbS:Cd sample
PbS:Sn 样本出现一条在费米能级Ef下方的与杂质相关的能带(图3),它与未掺杂PbS 超胞的价带形状完全相同. 文献[10]认为其原因是较高能级的Sn -s 能态从未掺杂样本的价带中推出;本研究的结果认为这个作用虽小,但导致了其带隙的相应减小. 在元素周期表中Cd 原子和Sn 原子位置很相近,但它们两者在掺杂中不同,如Cd-s 能态会出现在PbS:Cd 掺杂的导带中,因为Sn-s 能态本身位于更深的能级;由于没有Sn-s 能态参与,Pb -p 能态和Sn-p 能态组成了其导带区域.
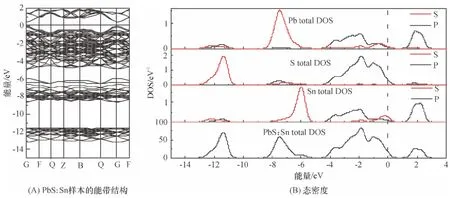
图3 PbS:Sn 样本的能带结构和态密度Figure 3 Band structures and density of states of PbS:Sn sample
然而Sb 是5 价电子的Ⅴ族元素;在掺杂替换Pb 的过程中它能带来自由电子并作为施主. 因此,它占据导带底的自由电子使费米能级移向导带区域,并最终表现出典型的n 型金属特性. 另一方面,价带和导带由于Sb 的掺杂同时向低能级移动,在图4A 中已清楚地显示了这一变化,另外看到较多的共振能级和一些费米能级附近的扁平能带的出现.PbS:Sb 掺杂的能带虽然有稍许向下的平移,PbS:Sb掺杂后价带与PbS:Sn 的相似.
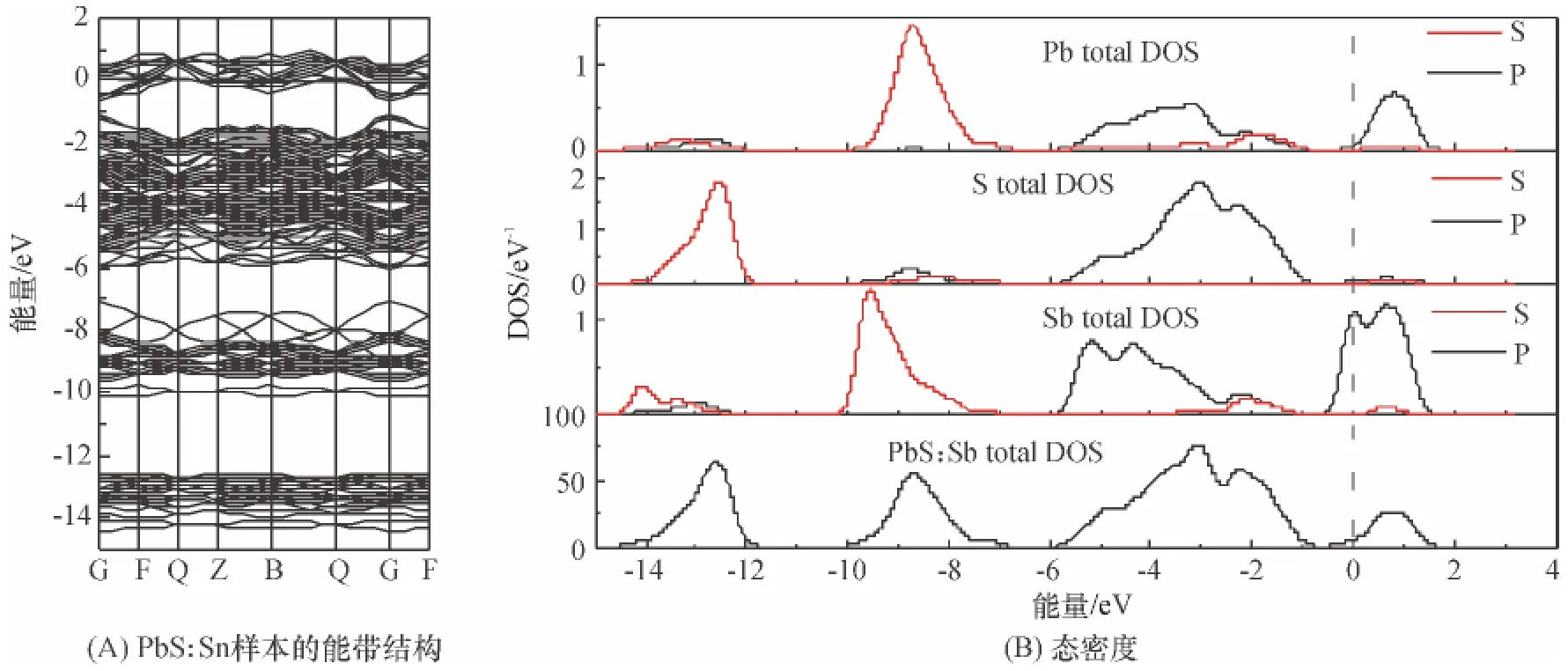
图4 PbS:Sb 样本的能带结构和态密度Figure 4 Band structures and density of states of PbS:Sb sample
2.2 光学性质
很多不同的实验方法已被应用到研究铅硫族化合物的光学性质中,如波长调制光谱法[26]、电吸收和电反射法[27]、反射和透射法[28]等. 根据卡多纳和格林纳韦的标记方法[28],本文定义ε2(ω)的主要峰值有:(1)第一序列峰E0,它基本和带隙值相对应;(2)幅度上最高峰E1,也称为反射峰;(3)能级范围内的E2高能级峰[4]. 图5 计算给出了未掺PbS 超胞、掺杂PbS:Cd、掺杂PbS:Sn、掺杂PbS:Sb 的ε2(ω)光谱. 未掺PbS 超胞、掺杂PbS:Cd 以及掺杂PbS:Sn的结果大体一致,因为它们在能带结构上相似,而能带结构又决定了光学跃迁[4];并且不同光谱峰的形成也可由能带至能带间的跃迁得到很好的解释. 在图5B 中,E1峰大约出现在2.95 eV,主要由在价带的S-p 轨道电子跃迁至在导带的Pb-p 轨道电子,形成价带和导带间类型的跃迁. E2峰大约出现在9.80 eV,由Pb -s 轨道电子激发至Pb -p 轨道上.比较前3 种情况的结果和未掺杂PbS 超胞的结果发现,第1个不同之处是掺杂PbS:Sb 的杂质能峰大约出现在0.60 eV,可能存在2个原因:(1)杂质能峰的产生可由杂质能级本身至导带底的激发形成(图4B). 通过前面Sb 的分析知道,杂质Sb -5p 轨道电子主要在费米能级附近,而且Sb 杂质使能带整体下移;(2)它也可由多个Sb 杂质5p 轨道之间的迁移形成. 第2个不同之处是掺杂PbS:Sb 的主峰E1红移,这可由其相对应的能带结构和态密度得出. 第3个不同之处是和其他掺杂类型相比,掺杂PbS:Cd 的最高峰E1最小,介电光谱的反射峰最小.其原因是位于导带的Cd -s 轨道影响了价带S -p轨道电子至导带Pb-p 轨道电子的跃迁.
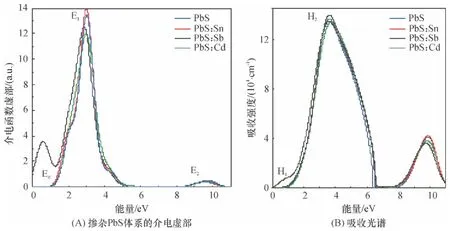
图5 掺杂PbS 体系的介电光谱和吸收光谱Figure 5 Imaginary parts of the dielectric function and absorption spectra of doped PbS systems
从图5B 中的吸收光谱可看到和前述类似的计算结果;掺杂PbS:Sb 的主吸收峰H2和杂质吸收峰H1相对于其他的掺杂会出现红移,这与得到的介电光谱虚部ε2(ω)原因一致. 同时,本掺杂体系的吸收光谱范围变宽. 目前通过理论和计算研究掺杂PbS 超胞体系的文献并不多,而本文得到的结果可与其他铅硫族化合物体系研究[4,26,29]进行比较,为后续的掺杂PbS 体系理论、实验研究提供有益的帮助.
3 结论
本文计算了掺杂PbS 体系的形成能、能带结构、态密度和相关的光学性质. 通过对不同掺杂位置的形成能的比较分析,得到了最稳定的掺杂结构. 从能带结构和态密度结果分析可知,掺杂后电子性质的变化可归纳为掺杂体系的带隙随着杂质的原子序数单调递减;掺杂的PbS:Cd 体系会出现稍扁平的能带;n 型的掺杂PbS:Sb 体系会出现共振能态、扁平能带. 在3 种掺杂体系中,Sb 掺杂的PbS 体系光学性质变化显著,主要包括介电光谱上的杂质峰及其红移、吸收带边的扩展. 另外,Cd 掺杂PbS 介电光谱的反射峰最小.
[1]Wood C. Materials for thermoelectric energy conversion[J]. Reports on Progress in Physics,1988,51(3):459-539.
[2]Hummer K,Grüneis A,Kresse G. Structural and electronic properties of lead chalcogenides from first principles[J]. Physical Review B,2007,75(19):5211 -5219.
[3]Zhao L D,He J Q,Hao S Q,et al. Raising the thermoelectric performance of p-type PbS with endotaxial nanostructuring and valence-band offset engineering using CdS and ZnS[J]. Journal of the American Chemical Society,2012,134(16):327 -336.
[4]Albanesi E A,Okoye C M I,Rodriguez C O,et al. Electronic structure,structural properties,and dielectric functions of Ⅳ-Ⅵsemiconductors:PbSe and PbTe[J].Physical Review B,2000,61(24):589 -595.
[5]Eto K,Taskin A A,Segawa K,et al. Spin-orbit coupling and anomalous angular-dependent magnetoresistance in the quantum transport regime of PbS[J]. Physical Review B,2010,81(16):12021 -12024.
[6]Hoang K,Mahanti S D. Electronic structure of Ga-,In-,and Tl-doped PbTe:A supercell study of the impurity bands[J]. Physical Review B,2008,78(8):5111 -5118.
[7]Zhao L D,Lo S H,He J Q,et al. High performance thermoelectrics from earth-abundant materials:Enhanced figure of merit in PbS by second phase nanostructures[J]. Journal of the American Chemical Society,2011,133(20):476 -487.
[8]Johnsen S,He J Q,Androulakis J,et al. Nanostructures boost the thermoelectric performance of PbS[J]. Journal of the American Chemical Society,2011,133(34):60 -70.
[9]Zhao L D,He J Q,Wu C I,et al. Thermoelectrics with earth abundant elements:High performance p-type PbS nanostructured with SrS and CaS[J]. Journal of the American Chemical Society,2012,134(79):2 -12.
[10]Peng H,Song J H,Kanatzidis M G,et al. Electronic structure and transport properties of doped PbSe[J].Physical Review B,2011,84(12):52071.
[11]John J,Zogg H. Infrared p-n-junction diodes in epitaxial narrow gap PbTe layers on Si substrates[J]. Journal of Applied Physics,1999,85(6):3364 -3367.
[12]Akimov B A,Dmitriev A V,Khohlov D R,et al. Carrier transport and non-equilibrium phenomena in doped PbTe and related materials[J]. Physical Status Solidi A,1993,137(1):9 -55.
[13]Springholz G,Schwarzl T,Heiss W,et al. Midinfrared surface-emitting PbSe/PbEuTe quantum-dot lasers[J].Applied Physics Letters,2001,79(9):1225 -1227.
[14]Clark S J,Segall M D,Pickard C J,et al. First principles methods using CASTEP[J]. Zeitschrift für Kristallographie,2005,220(5):567 -570.
[15]Segall M D,Lindan P J D,Probert M I J,et al. Firstprinciples simulation:Ideas,illustrations and the CASTEP code[J]. Journal of Physics:Condensed Matter,2002,14(11):2717 -2744.
[16]Monkhorst H J,Pack J D. Special points for Brillouinzone integrations[J]. Physical Review B,1976,13(12):5188 -5192.
[17]Ekuma C E,Singh D J,Moreno J,et al. Optical properties of PbTe and PbSe[J]. Physical Review B,2012,85(8):2051 -2057.
[18]Van de Walle G C,Neugebauer J. First-principles calculations for defects and impurities:Applications to Ⅲ-nitrides[J]. Journal of Applied Physics,2004,95(8):3851 -3879.
[19]Sarmadian N,Saniz R,Lamoen D,et al. Influence of Al concentration on the optoelectronic properties of Al-doped MgO[J]. Physical Review B,2012,86(20):51291 -51295.
[20]Cantele G,Degoli E,Luppi E,et al. First-principles study of n-and p-doped silicon nanoclusters[J]. Physical Review B,2005,72(11):33031 -33034.
[21]Luo B,Wang X,Zhang Y,et al. First principles study of structural,electronic and optical properties of Pb doped SrHfO3[J]. Materials Chemistry and Physics,2012,133(2/3):857 -862.
[22]Zhang C,Wang C L,Li J C,et al. Substitutional position and insulator-to-metal transition in Nb-doped SrTiO3[J]. Materials Chemistry and Physics,2008,107(2/3):215 -219.
[23]Zhang Y,Ke X,Chen C,et al. Thermodynamic properties of PbTe,PbSe,and PbS:First-principles study[J].Physical Review B,2009,80(2):401 -412.
[24]Wei S H,Zunger A. Electronic and structural anomalies in lead chalcogenides[J]. Physical Review B,1997,55(20):605 -610.
[25]Albanesi E A,Peltzery Blanca E L,Petukhov A G. Calculated optical spectra of IV-VI semiconductors PbS,Pb-Se and PbTe[J]. Computation Materials Science,2005,32(1):85 -95.
[26]Kohn S E,Yu P Y,Petroff Y,et al. Electronic band structure and optical properties of PbTe,PbSe,and PbS[J]. Physical Review B,1973,8(4):1477 -1488.
[27]Aspnes D E,Cardona M. Electro-optic measurements of PbS,PbSe,and PbTe[J]. Physical Review,1968,173(3):714 -728.
[28]Cardona M,Greenaway D L. Optical properties and band structure of group Ⅳ-Ⅵ and group V materials[J].Physical Review,1964,133(6A):A1685 -A1697.
[29]Rached D,Rabah M,Benkhettou N,et al. Calculated band structures and optical properties of lead chalcogenides PbX (X=S,Se,Te)under hydrostatic pressure[J]. Physica B:Condensed Matter,2003,337(1 -4):394 -403.

