线面平行的证明问题中的“V字形”和“T字形”
雷雄军
摘 要:立体几何是高考数学的重要考点,在广东高考题中,一般占14分.立体几何的证明通常涉及平行和垂直问题,平行问题中线面平行是常见的出题方向.在线面平行的证明中,学生对于要通过作辅助线构造线线平行问题很多时候都不能顺利证出.通过平常教学工作的积累,发现了线面平行证明的两种类型,并且得出相应的解决方案.以高考题及其模拟题为例子详细阐述了线面平行问题中的“V字形”和“T字形”并给出了对应的解法.多年的教学实践证明,“V字形”和“T字形”的使用使学生对线面平行证明思路更加清晰
简单.
关键词:线面平行;“V字形”;“T字形”
在立体几何这块的复习过程中,学生对于平行证明一般都掌握得比较好,因为不管是线面平行还是面面平行问题,考查的难度都不大。特别是线面平行,学生平时训练得比较多,但是平时的大量练习很多时候也造成了学生的混乱,在需要通过辅助线来构造线线平行的时候,学生就不知道到底该怎么添加辅助线.因此,学生经常会出现老师一讲就会,自己做又不知道从什么地方下手的状况.笔者在平常的教学过程中针对学生的这种现象,发现了线面平行问题中的“V字形”和“T字形”,这两种类型给学生如何添加辅助线构造线线平行提供了方向.
一、“V字形”线面平行的证明
什么是“V字形”呢?我们先来看下面的例子.
例题1.1 (2013年惠州二模第18题)如下图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.
(1)求证:AB1∥平面BC1D;
(2)若BC=3,求三棱锥D-BC1C的体积.
本题第一问考查的就是线面平行的判定.要证平面AB1∥平面BC1D,所以一定要在面BC1D找线和AB1平行.又给出了AC的中点,AB1和AC相交成一个“V”字,因此我把此种类型称为“V字形”.“V字形”就是题目中要证的线与题目中给出中点的线相交成“V”字.对于这种题目,一般可以引导学生对“V”字封口构造三角形,然后将连线的中点与已知的中点相连就出现了三角形的中位线.如上面的例子中,取连线CB1的中点O与AC的中点D连接.那么利用三角形的中位线的性质就在面BC1D内找到了线OD∥AB1,证明过程如下:
(1)证明:连接B1C,设B1C与BC1相交于点O,连接OD.
∵四边形BCC1B1是平行四边形,
∴点O为B1C的中点.
∵D为AC的中点,
∴OD为△AB1C的中位线,∴OD∥AB1.
∵OD?奂平面BC1D,AB1?埭平面BC1D,
∴AB1∥平面BC1D.
“V字形”虽然一般的情况下要做两条辅助线,一条是封住“V”的口,一条是两个中点相连.这两条辅助线比较容易找,所以此种题型的平行证明难度不是很大,很多地方的考题比较喜欢设计这种类型的问题放在第一问.如:
例题1.2 (新课标2013卷文科18题)如下图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.
(1)证明:BC1∥平面A1CD1;(2)略.
在第一问中,BC1与中点边线AB构成了“V”字,只要连接AC1与A1C相交于点O,连接OD,则OD∥BC1,这个命题就得证.
再比如,下面这道2013年广州一模试卷18题也是明显的“V字形”.
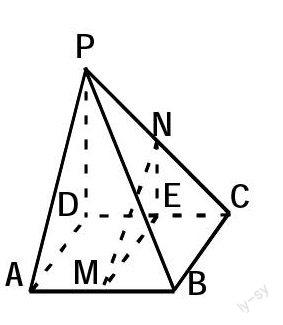
例题1.3 (2013年广州一模18题)如下图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=60°,AC=2AD,PD⊥平面ABCD,点M为PC的中点.
(1)求证:PA∥平面BMD;
(2)求证:AD⊥PB;
(3)若AB=PD=2,求点A到平面BMD的距离.
第一问的解答只需要连接AC,然后再把AC的中点与M相连即可.
二、“T字形”线面平行的证明
前面我们提到,“V字形”虽然在一般的情况下要做两条辅助
线,但是这两条辅助线还是比较容易找到.因为只要封口取中点就可以得到两条辅助线.在下面的这个例子中也给出了线的中点,但是要证的线和有中点的线不是相交成“V字形”,而是“T字形”.
例题2.1 (2013年江门调研17题)如下图,四棱锥P-ABCD的底面是边长是1的正方形,侧棱PD⊥平面ABCD,M,N分别是AB,PC的中点.
(1)求证:MN∥平面PAD;
(2)记MN=x,V(x)表示四棱锥P-ABCD的体积,求V(x)的表达式(不必讨论x的取值范围).
第一问要证明的线MN与给的中点的线PC相交成“T”字.
我们把这种类型称为“T字形”.一般学生对这种问题感觉比较棘手.
对于这种问题一般可以采取两种解法快速解决,一种是构造平行四边形,利用对边平行找到要证的线与面内的线平行.另一种可以通过构造面面平行,然后利用“两个平面平行,则一个面内的任意一条线和另外一个平面平行”加以解决.大部分时候两种方法都可以找到线线平行,但是有时候也只有一种方法能够找线线平行,所以平常两种做法一起使用.
如,上面这道题我们可以取PD得中点E,连接AE,NE,则由NE和AM平行且相等可以得出四边形AMNE为平行四边形,所以得出MN∥AE,进而得到MN∥平面PAD.具体过程如下:
在这个方法中,学生可能对如何找到平行四边形比较费劲,通常可以提示学生先用尺子把MN往面内移就可以得到平行四边形.
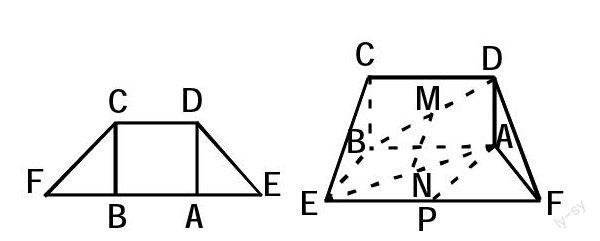
第一问线面平行的问题,我们可以采用第一种方法取BC,FB的中点G,H.连接GN,GH,MH通过证明四边形MNGH为平行四边形得证.也可以通过取AB的中点O,连接OM,ON构造平面OMN∥平面FBC得证.
再如下面这道山东高考题:
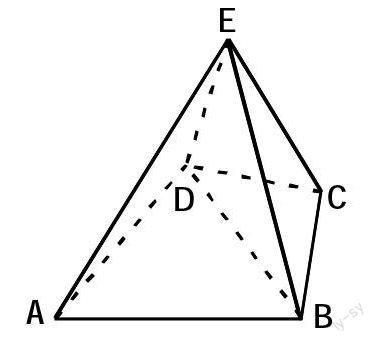
例题2.3 (2012年山东高考题文科卷19题)如图,几何体E-ABCD是四棱锥,△ABC为正三角形,CB=CD,EC⊥BD.
(Ⅰ)求证:BE=DE;
(Ⅱ)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
第二问的证明也为我们的“T字形”,但是这道题构造平行四边形不是那么简单,而通过取AB的中点N.
构造平面MND∥平面BCE比较简单(如下图所示).
所谓条条大路通罗马,不管走那条路,作为老师,应该把如何上路的方法揭示出来,而不是把学生直接送到那条路上.线面平行證明中巧妙的添加辅助线会给解题带来很大的便捷.如果我们只告诉学生如何添加辅助线,而不分析为什么及什么时候这样添加辅助线,那么学生解决此类问题还是只能依赖灵感的乍现.“V字形”和“T字形”明确地指出了在遇到类似问题时候如何构造辅助线,使学生在解决此类问题事半功倍!

