基于区域滤波的GOCE稳态海面动力地形和地转流
白希选,闫昊明,朱耀仲,彭鹏
1 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室,武汉 430077 2中国科学院大学,北京 100049
1 引言
稳态海面动力地形(Mean Dynamic Topography,简称MDT)是指平均海面高(Mean Sea Surface)相对于大地水准面(geoid)的差异,在全球起伏约1~2m,在地转平衡的近似下,其梯度对应于海洋表层地转流.MDT对于地球形状、全球高程基准统一、大地水准面求定、地球重力场模型精化和洋流、潮汐的确定,以及海洋环境的监测等研究都具有重要的意义和作用(管泽霖等,1996;李建成等,2003).对于MDT的确定,传统海洋学方法,一般利用观测的海水温度和盐度资料来计算(侍茂崇,2004).这种方法需要设定实际情况下并不存在的海水无运动面作为参考基准面,仅能计算由非均匀密度场引起的MDT,且存在数据采集困难,存在数据偏差和数据空白区等问题,极大地限制了其广泛应用.相比之下,利用卫星测高和卫星重力数据来计算MDT的卫星大地测量法,具有观测精度高、连续性好、全球覆盖等优势.随着卫星大地测量学的发展,海面高度场和大地水准面的精度和分辨率得到了大幅提高,直接计算MDT的条件已经成熟.
利用卫星大地测量法直接确定MDT,必要条件是要有高精度高分辨的平均海面高度场和大地水准面.目前CNES(Centre National d′Etudes Spatiales)解算的平均海面高网格数据的空间分辨率优于4km,精度优于5cm(Schaeffer et al.,2012);对于大地水准面,EGM2008重力场模型已经达到了2190阶,对应的空间分辨率约为10km,精度为5~10cm(Pavlis et al.,2011),已经满足了计算 MDT的条件.但EGM2008模型本身融入了测高数据,因此,用它计算得到的海洋区域大地水准面与卫星测高数据高度相关,使得MDT缺乏独立性.为了克服这种缺陷,迫切需要独立的大地水准面数据.因此,独立观测的卫星重力数据成为求解大地水准面的首选.目前,利用2003—2010年间累积了8年的GRACE(Gravity Recovery and Climate Experiment)重力资料,可以获得最高阶次为180阶的平均重力场(Mayer et al.,2010),其对应的大地水准面空间分辨率为110km.2009年,搭载了重力梯度计的GOCE(Gravity field and steady-state Ocean Circulation Explorer)卫星发射以后,获取了对高阶重力场敏感的重力梯度数据,使地球平均重力场模型的精度和分辨率进一步得到大幅提高(Rummel,2010;Rummel et al.,2011;Yi et al.,2013).目前纯GOCE卫星重力场的最高阶次达到280阶,对应的空间分辨率约为70km(72km).纯卫星重力场空间分辨率低于卫星测高数据,难以直接应用于小尺度MDT的确定,却可以很好地满足直接确定大中尺度MDT所需要的条件.在此基础上,还可以通过地转平衡方程,利用MDT来独立确定大中尺度地转流信息.
自2002年GRACE重力场数据,尤其是2009年GOCE静态重力场数据公布以后,大中尺度MDT确定以及相应的地转流研究得到了快速发展.Bingham等(2011)利用由仅2个月的GOCE数据解算的静态重力场,给出了北大西洋MDT及其地转流的初步估计,其精度优于采用8年GRACE观测数据得到的结果,证明了GOCE在高阶静态重力场精度上超过了GRACE;Knudsen等(2011)利用2个月的GOCE数据计算了全球的MDT,并与Maximenko等(2009)解算的 MDT模型进行了对比分析;Albertella等(2012)利用由12个月GOCE数据解算的重力场模型计算了高分辨率的南大洋稳态MDT;Farrell等(2012)利用联合 GRACE和GOCE数据解算的GOCO02S重力场模型计算了北极区域的洋流;Mulet等(2011)通过将不同GOCE重力场模型计算的MDT模型与实测数据进行对比,评估了GOCE大地水准面的精度;万晓云和于锦海(2013)分析了由不同GOCE引力场模型解算的MDT精度的稳定性;彭利峰等(2013)基于空域法,利用由18个月GOCE数据解算的重力场模型确定了大于400km尺度的MDT信号.为了更好地确定全球和区域MDT及其对应的地转流,本文采用能够有效抑制误差,提高空间分辨率的频域法(Bingham et al.,2008)来求解 MDT.此外,在MDT的求解中,空间滤波尺度对MDT的影响比较大,我们通过与全球漂流浮标数据进行对比分析,提出了按区域、纬度带和全球分别确定MDT滤波尺度因子的方法,获得了精确的高分辨率MDT,并对MDT和其对应的地转流给出了详细分析和讨论.
2 数据资料
在平均海面高度数据方面,本文采用了由CNES利用16年卫星测高数据解算的CNES_CLS2011_MSS模型.该模型数据是2′×2′网格形式,对应的空间分辨率约为3.7km,覆盖了80°S至84°N间的海洋区域(Schaeffer et al.,2012).
由于重力场模型是确定高精度MDT的另外一个主要因素,为了选择一个合适的重力场模型,我们首先对多个机构发布的 GO-CONS-GCF-2-TIM4模型(TIM4模型)、GO-CONS-GCF-2-TIM5模型(TIM5模型)、GGM05S模型、EIGEN4S1模型和ITG-GRACE2010S模型(ITG2010S模型)等纯GOCE和GRACE重力场进行对比分析,各重力场模型对应的大地水准面的精度如图1所示.在GOCE重力场模型方面,TIM5的精度整体高于TIM4模型,为此我们选用了TIM5模型;在GRACE重力场模型精度方面,在60阶以下,各GRACE重力场模型的精度均优于0.2cm,对MDT的计算影响不大,在60阶以上,ITG2010S模型的精度最高,因此我们选用了ITG2010S模型.TIM5 GOCE重力场模型是GFZ公布的,该模型利用
3 稳态海面动力地形和地转流
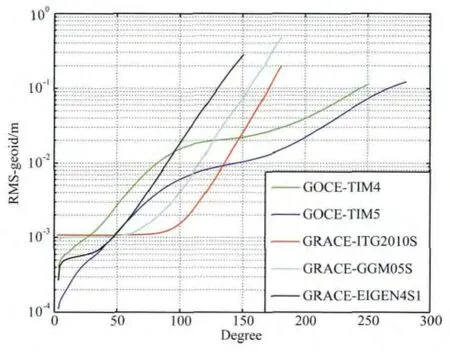
图1 GOCE和GRACE重力场模型的大地水准面累积误差Fig.1 Cumulative geoid errors of GOCE and GRACE gravity models
2009年11月到2013年10月间的42个月的GOCE数据得到,最高阶数为280阶(Pail et al.,2010;Brockmann et al.,2014).ITG2010S 模 型 由ITG(Institude of Theoretical Geodesy,University of Bonn)公布,该模型利用8年GRACE数据解算得到,最高阶数为180阶.如图1所示,在高阶部分(>140阶),GOCE大地水准面累积误差远低于GRACE结果;在中低阶部分(50~140阶),GOCE大地水准面累积误差略大于GRACE结果,但其误差小于1cm,可以满足在中低阶计算海面动力地形的要求.
在分析MDT精度及其对应的平均地转流场误差时,我们还要用到实测浮标数据计算的浮标稳态地转流场.计算浮标稳态地转流场时,需要从浮标流速中扣除由风速引起的Ekman流速和时变地转流速.因此需要漂流浮标轨迹、海洋表层风场和海面高度异常资料.浮标轨迹资料为由NOAA(National Oceanic and Atmospheric Administration)提供的沿浮标轨迹位置和流速数据(ftp.aoml.noaa.gov/phod/pub/buoydata),其时间分辨率为6h(Lumpkin and Pazos,2007);海洋表层风场数据为NOAA提供的海表10m风速数据(http:∥www.esrl.noaa.gov),空间分辨率为2.5°,时间分辨率为6h(Kalnay et al.,1996);海面高度异常资料为 AVISO(Archiving,Validation and Interpretaion of Satellite Oceanographic data)提供的0.25°空间分辨率网格数据(ftp:∥ftp.aviso.oceanobs.com),时间分辨率为7天(Dibarboure et al.,2008);以上数据的时间起止点为1992年10月至2012年12月.
根据稳态海面动力地形的定义,其计算公式为:

式中,η为稳态海面动力地形,H为平均海面高,N为大地水准面高.由于平均海面高和大地水准面的数据源分别表现为空域网格和频域球谐系数形式,因此产生了两种求解海面动力地形的方法.一为空域法,即将大地水准面频域球谐系数转换到空域网格,然后直接应用公式(1)在空域内求解 MDT;另一方法为频域法,即首先将海面高空间网格数据按照公式(2)在球面展开为频域球谐系数格式,在频域内与对应的大地水准面球谐系数相减,得到MDT频域球谐系数,再按照公式(3)进行球谐合成得到空域MDT.空域海面高度场转换为频域球谐系数公式和频域稳态海面动力地形转换为空域网格公式分别为:分别为平均海面高和MDT对应的球谐系数.
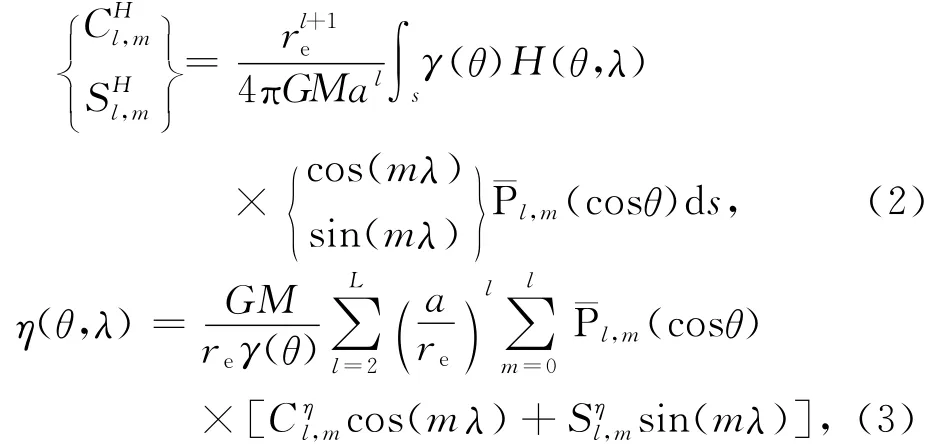
本文在计算MDT时,采用的是频域法,这种方法可以在频域内对高空间分辨率的平均海面高信号进行低通滤波,通过将平均海面高度场展开至与重力场相同的阶次,严格保证了平均海面高截断误差与大地水准面截断误差的一致性,可以有效抑制初始MDT中的大地水准面截断误差,并在MDT的进一步滤波处理中,可以通过较小的空间滤波尺度获得更精细的 MDT特征(Bingham et al.,2008).计算中,首先将平均海面高度模型重采样至0.5°×0.5°的网格形式,然后再对其进行球谐截断计算.由于空间数据展开到频域球谐系数需要全球网格数据,而平均海面高数据仅在海洋上有数据,为此我们
式中,re为椭球面上的地心距离,a为参考椭球的长半轴,(θ,λ)为球心余纬和经度,(l,m)为球谐系数的阶和次,γ是纬度的函数,代表椭球面上的正常重力值,GM为地球引力质量常数,为规则化的连带勒让德函数,η为 MDT,H为平均海面高度,采用与海面高度场相似的大地水准面高度(由计算MDT采用的对应重力场模型得到)来覆盖无海面高度的区域,从而合成全球覆盖的海面高度场H,并利用公式(2)来得到频域球谐系数.这种全球覆盖的海面高度场,可以在空域到频域转换的计算中有效减小 Gibbs抖动噪声(Bingham et al.,2008),但不能完全消除海陆边界不连续处的Gibbs抖动产生的假频信号(Albertella and Rummel,2009).对于海陆边界不连续产生的假频信号,我们将通过球谐函数多次迭代的方法来进一步抑制(Albertella and Rummel,2009;Albertella et al.,2010).得到全球覆盖海面高度场的频域球谐系数后,就可以与对应的大地水准面球谐系数相减,得到MDT球谐系数,然后按公式(3)将其合成为空间网格,得到初始的MDT.为了尽可能保留高分辨率的大地水准面信号,在MDT计算时,选定的MDT截断阶次为重力场模型的最高阶次.由于国际上通用的GUT软件中的频域法程序并不严格符合频域法的定义,其对应的地转流结果存在流幅偏大速度偏低等问题,我们在频域法计算中采用了自主编写的程序,针对GUT软件的问题进行了相应的处理.
获得MDT后,根据地转平衡理论,可得到对应的地转流.除赤道和近岸区域,海水长时间大规模的流动处于地转平衡状态(张子占等,2007),其地转平衡公式为:
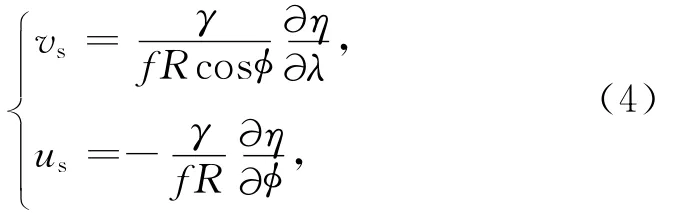
式中,f=2ω·sinφ为科氏力,ω为地球自转速率,φ为纬度,vs和us分别为地转流速度的南北向分量(北向为正)和东西向分量(东向为正).需要注意的是,由于赤道附近科氏力f趋近于0,地转平衡公式存在奇异性,所以计算中去除了赤道附近南北纬4°间的区域.
地转流还可以通过漂流浮标得到.表层漂流浮标又被称为拉格朗日浮标,其浮筒悬浮在15m的水深处,与表层的洋流运动一致(Niiler and Paduan,1995).漂流浮标运动的组成十分复杂,其流速包含地转流速和非地转流速.地转流速包含稳态地转流和时变地转流,非地转流速包含Ekman流速和其他高频运动导致的流速噪声(Rio and Hernandez,2004).要计算稳态地转流场,需要从浮标流速中扣除时变地转流、Ekman流和其他洋流高频噪声.我们依据Ralph和Niller(1999)模型和Niller(2001)给出的模型参数,将表层风场数据插值到浮标位置,计算出Ekman流速,然后从浮标流速中扣除.时变地转流是地转流的时变部分,符合地转平衡条件,可由测高数据得到的海面高度异常资料(SLA),根据地转平衡公式(4)计算得到,将其插值到对应时间的浮标位置上后,从以上结果中扣除.表层海水的高频运动包含惯性振荡、潮流、内波、近岸上升流、旋转波等,具有频率高、周期短的特点.为此,我们沿浮标轨迹,对流速进行了三天时间平均来抑制流速噪声,得到稳态的浮标地转流速.将1992年至2012年间的107163234个浮标流速值,经网格平均后,给出了0.5°×0.5°网格形式的稳态浮标地转流场.如图2所示,除赤道和两极冰架区域外,该浮标地转流场基本上覆盖了全球海洋,且清晰地显示出了全球的主要洋流系统.为检验其可靠性,我们与 Mulet等(2011)计算的地转流场进行了对比,其差异的均方根为3.79cm·s-1,即与 Mulet等(2011)中的地转流场十分接近.
4 海面动力地形滤波尺度
采用公式(1),在频域内从平均海面高中扣除大地水准面后,转化至空域即可得到MDT.我们基于GOCE(280阶,70km空间分辨率)和GRACE(180阶,110km空间分辨率)重力场,分别计算了相应的0.5°×0.5°网格的 MDT (图略).这两种 MDT的大尺度特征一致(对应精度较高的低阶球谐系数)(张子占和陆洋,2005),但中小尺度的信号(对应高阶球谐系数)均含有大量高频噪声,因此需要进一步的滤波处理,才能对其进行具体的对比分析.由于频域内滤波会使近海的MDT信号向陆地泄露,为避免这种泄露造成的近海MDT信号失真,在此选用空域滤波,滤波时陆地区域的值不参与计算.在滤波过程中,采用的是空域高斯核函数滤波器,该滤波器的效果主要取决于滤波尺度因子(滤波半径)的选择(Jekeli,1981;Wahr et al.,1998).因此,MDT 的滤波处理,主要在于确定合适的空间滤波半径.如果滤波半径较大,则在去除 MDT高频噪声的同时,也会使MDT的真实信号衰减;如果滤波半径较小,则不能很好抑制高频噪声.为了确定最优的空间滤波半径,我们以图2中的稳态浮标地转流场作为参考基准,通过公式(4)来求解滤波后 MDT对应的地转流,并与图2结果进行比对,就可以得到最优的滤波因子.值得注意的是,稳态浮标地转流场存在由浮标观测偏差引起的虚假趋势,也存在附带的改正误差(Rio et al.,2011;Grodsky et al.,2011),但因为稳态浮标地转流场是唯一独立且全球覆盖的洋流直接观测结果,采用其作为比对标准是合适的.
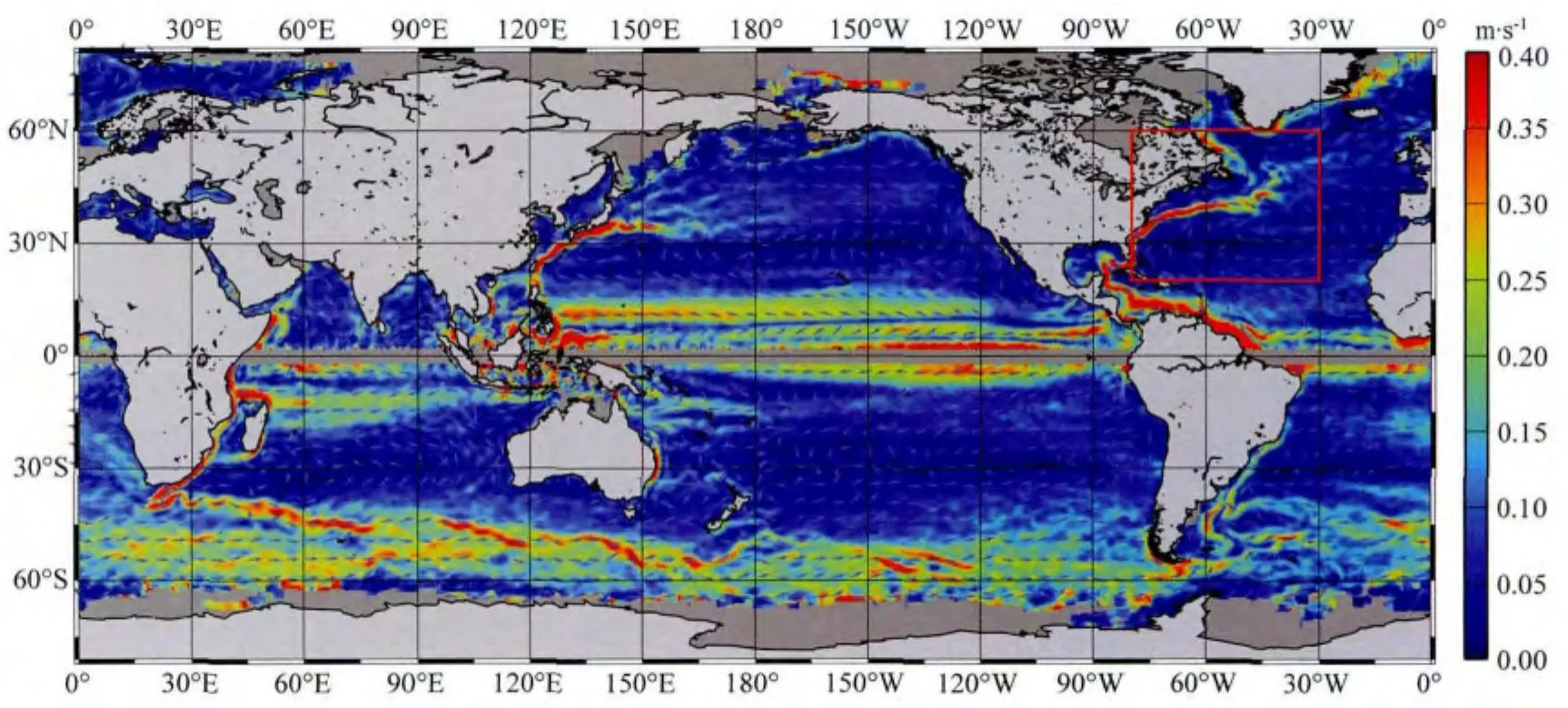
图2 稳态的浮标地转流场颜色表示流速的大小,箭头方向与地转流方向一致.Fig.2 The geostrophic current derived from buoys The speed is represented by color,while the geostrophic current direction is displayed by arrows.
4.1 区域滤波尺度
为确定最优的MDT区域滤波尺度因子,我们采用从10km至300km的高斯滤波半径,以10km为步长,对由公式(1)直接得到的MDT进行滤波,然后利用公式(4),得到对应的地转流,并与稳态浮标地转流场做对比,以二者差异的均方根最小时的滤波半径作为最优滤波半径,从而确定最优的区域滤波尺度因子.
首先以北大西洋区域(20°N—60°N,280°E—330°E)为例(图2红色方框区域),来确定该区域的最优滤波尺度因子.无论是从GOCE重力场,还是GRACE重力场得到的地转流结果,在MDT滤波半径的变化上,都表现出了统一的规律,即在滤波半径从10km逐渐增加到300km的过程中,MDT得到的地转流和稳态浮标地转流的均方根,随着滤波半径的逐渐增大,迅速减小,高频噪声得到有效抑制;在达到最优滤波半径后,该均方根开始缓慢增大,真实信号衰减带来的误差逐渐显现.在此区域,GOCE和GRACE结果的最优滤波半径分别为90km和110km,说明由于GOCE结果有更高精度的相对高阶重力场信息,因此应用较小的滤波半径,就可以有效抑制相应的高频噪声.从图3中可以明显看出,在滤波半径小于40km的时候,GOCE数据中存在更多的高频噪声,其地转流对应的均方根明显大于GRACE结果;但当滤波半径大于40km直到最优滤波半径区间,GOCE重力场中的高频信号的精度明显高于GRACE结果(表现为均方根更小),这与图1是互相印证的,说明MDT的滤波半径与重力场中高频信号的精度密切相关,也说明GOCE和GRACE的主要差别在于高频信号的空间观测精度.对于滤波半径大于150km的低频信号,二者对滤波半径的响应无明显区别(图3).
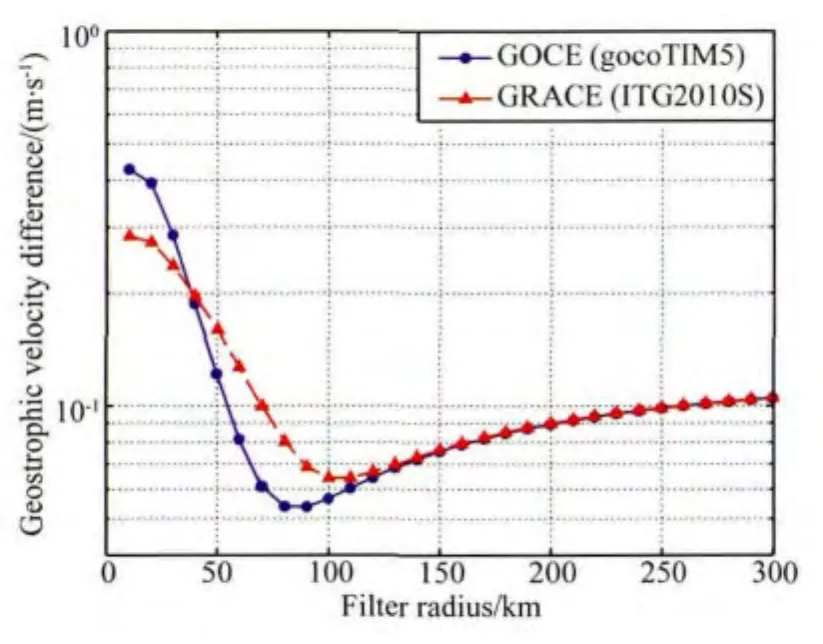
图3 北大西洋区域,从MDT得到的地转流场与浮标地转流场差异的均方根蓝线和红线分别代表采用的是GOCE和GRACE重力场得到对应的结果.Fig.3 The RMS difference between geodetic geostrophic currents and buoy geostrophic currents The blue and red dash line represents the RMS result derived from GOCE and GRACE gravity field,respectively.
为了进一步分析全球不同区域MDT的最优滤波尺度因子,我们按照北大西洋区域的分析步骤,对在全球海域内按网格区域分析了最优滤波半径.在增大网格区域保证网格内的RMS值具有较高的统计意义,和减小网格区域突出区域性差异的平衡下,选择了10°×10°的网格进行分析.对比 MDT滤波半径分布(图4)和浮标地转流场(图2),可以获得以下结果:(1)相对于弱流区域,强流区的最优滤波半径较小.在强流区域,如果采用更大的滤波半径,就等价于在谱域内去掉高阶球谐系数,从而造成这部分高阶有效信号丢失,引起截断误差明显增大,最终引起该区域均方根变大;在弱流区域,高阶信号比较小,其截断误差效应也就相应地比较小,因此滤波半径相对较大.(2)总体来讲,最优滤波半径在中高纬度区域要小于低纬度区域.这主要是重力卫星观测数据量随着纬度的升高而逐渐增大,导致其解算精度及对应的大地水准面在中高纬度区域较高(Pail et al.,2010;Wahr et al.,2006),因此较小的滤波半径就可以获得最优的地转流结果.(3)在南极绕流区域,局部出现非常大的滤波半径,主要原因是该区域地转流场十分复杂,而且浮标观测值很少,由浮标计算的地转流场的误差偏大.此外,在局部弱流区,如西太平洋暖池中心、东太平洋弱流区、南大洋弱流区等区域,最优滤波半径接近300km,此时这些区域的MDT信号几乎完全被平滑掉.对于这些弱流区域,在滤波半径达到200km左右时,其RMS结果与300km的滤波半径结果没有显著差别(图略),因此在实际中采用200km的滤波半径就足以滤去高频噪声.
4.2 纬度带和全球滤波尺度
在全球区域滤波尺度分析的基础上,我们进一步分析了纬度带和全球的最优滤波尺度因子,通过面积加权的方法,给出了低、中、高纬度带和全球的平均最优滤波尺度因子(表1).此外,由于弱流区和南极绕流区局部区域的滤波半径的置信度较弱,在计算表1时,将大于200km的滤波半径设置为200km.在全球尺度上,GOCE海面动力地形的滤波半径(127km)比GRACE结果(154km)小27km,结合图1,可以充分说明较高精度的高阶GOCE重力场数据提高了海面动力地形的空间分辨率,进而也提高了对应的地转流场分辨率.这种空间分辨率的提高,也非常清楚地体现在了所有的纬度带最优滤波半径上(表1),且无论是全球还是纬度带,应用GOCE重力场数据得到的MDT及其地转流在空间分辨率上提高了21~27km.
5 海面动力地形和洋流
5.1 海面动力地形
应用4.2节得到的MDT全球最优滤波半径,采用高斯滤波方法和GOCE重力场,可以得到MDT在全球的分布(图5a).相比滤波前的结果(图略),滤波后MDT中的高频噪声已经得到有效抑制,全球MDT的主要起伏特征已经十分显著,例如,从图5a中可以清楚看到由暖水汇聚形成的高起伏大洋西部暖池,及在近极区域由冷水辐散形成的低起伏区域.MDT表现出了清楚的纬度特征,即从赤道区域到中低纬度区域,再到高纬度区域,MDT呈现出低-高-低的态势.在南极绕流区域,MDT趋向于均匀一致,而在太平洋和大西洋区域,MDT则存在明显的从西向东逐渐减小的趋势.因此,无论是纬向还是经向,MDT都具有明显的细节特征.
5.2 洋流
由图5a,应用公式(4)就可以得到由MDT确定的全球地转流(图5b).对比由MDT获得的地转流场(图5b)和浮标地转流场(图2),可以看出二者在整体上非常一致,只是在强流区,MDT得到的地转流流速值要小于浮标地转流的结果.总体来讲,由MDT确定的地转流可以清晰准确地反映全球洋流的主要特征,如北太平洋西边界流(黑潮)、北赤道流、墨西哥湾流、加利福尼亚流、南赤道流、绕极流及近极流等主要洋流.
为了定量分析MDT对应的地转流场与浮标地转流场的关系,我们根据全球浮标地转流流速的标准差(9.5cm·s-1)和区域强流的多个横剖面结果(图略),假定强流的最低边界流速为10cm·s-1,并定义此区域为流轴区域,以此为标准,首先给出北大西洋区域的结果 (图6,图7).无论是浮标地转流场,还是MDT得到的地转流场,都抓住了墨西哥湾暖流和拉布拉多寒流的主要特征,且浮标地转流场的流轴区域(>10cm·s-1)明显大于GOCE结果,而GOCE得到的流轴区域又略大于GRACE对应的结果(图6).在北大西洋区域,GOCE和GRACE对应的地转流场与浮标地转流场的相关系数均超过0.8,说明MDT得到的地转流场与浮标地转流场具有很好的相关性.但在格陵兰寒流和加拿大北部的拉布拉多寒流区域,浮标地转流的流轴区域范围大;GOCE得到的地转流场,只能清晰显现小范围的格陵兰寒流流轴;而GRACE对应的地转流则在上述区域几乎看不到任何强流特征.此外,在墨西哥湾暖流与拉布拉多寒流的交汇区,浮标地转流的细节特征更加明显(图6).
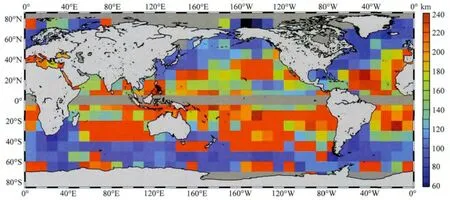
图4 采用GOCE重力场得到的全球区域海面动力地形的最优滤波半径Fig.4 Regional optimal filter radius of GOCE MDT
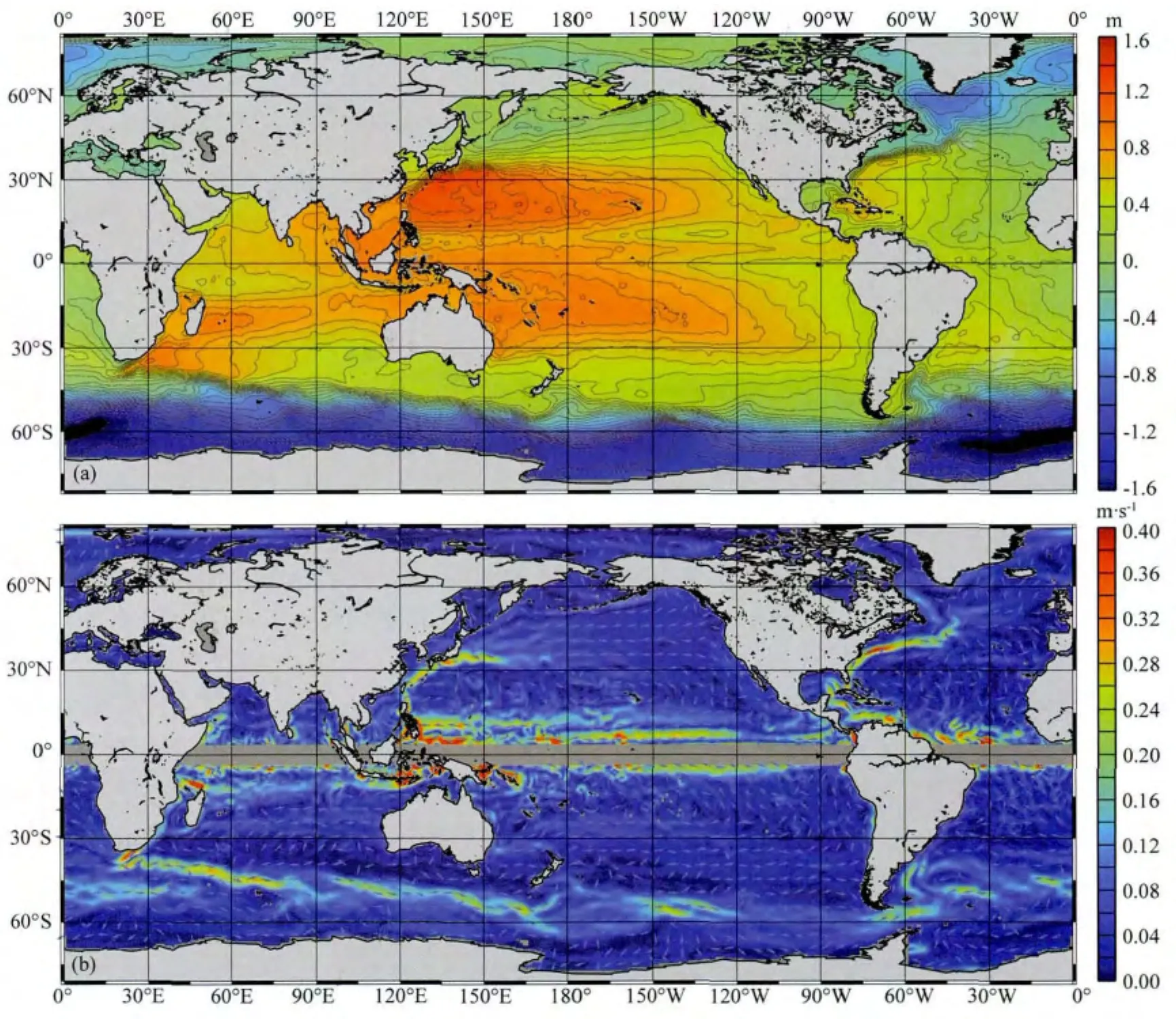
图5 (a)GOCE海面动力地形,(b)GOCE地转流场,颜色表示流速值,箭头方向与地转流方向一致Fig.5 MDT (a)and surface geostrophic currents(b)derived from GOCE,the speed is represented by color while the current direction is displayed by arrows
为了更直观地分析GOCE和GRACE得到地转流场的强流特征,在北大西洋流区,我们以浮标流轴区域为基准,计算了通过MDT(分别包括GOCE和GRACE结果)得到的地转流速相对于浮标地转流速的比例(图7).在此区域,总体上MDT得到的地转流场流速都小于浮标地转流场流速;但在部分流轴的两侧边缘区域,譬如部分墨西哥湾流流轴的两侧,MDT得到的地转流场流速则略大于浮标地转流流速.在图7的流轴区域,从GOCE和GRACE得到的平均地转流流速,分别为浮标地转流流速的75%和67%,说明GOCE对应的地转流场在流速上相比GRACE结果平均提高了8%.参照图7c,可以看到,这一提高的比例在格陵兰寒流区域甚至达到了40%.此外,GOCE和GRACE得到的地转流场与浮标地转流场差异的均方根分别为5.38cm·s-1和6.42cm·s-1,GOCE的结果比 GRACE的结果相比约减小了16%.上述各种分析结果,都说明了GOCE得到的地转流场在该区域都明显好于GRACE结果,与浮标地转流场更加接近,这与图1的结果是互相印证的,证明了较高精度的高阶重力场可以明显提高MDT和洋流结果.
参照上面北大西洋流区的地转流对比分析方法,我们对其他强流区(包括南极绕流区、黑潮区、阿古拉斯流区和北赤道逆流区)及不同纬度带的洋流也进行了类似的分析(表1).可以看到:
(1)在中高纬度区域的强流区,MDT(分别包括GOCE、GRACE结果)得到的地转流场与浮标地转流场的相关系数为0.64到0.94,说明MDT得到的地转流场与浮标地转流场在空间分布特征上,具有很好的一致性.在东西方向地转流占主导地位的赤道逆流区,东西分量的流速高度相关,而南北方向的流速则呈现出不相关的特点,造成这一现象的主要原因是赤道逆流区流速的南北向分量在流速中的比重十分低.对比GOCE和GRACE对应的相关系数发现:在南极绕流区、北大西洋流区和阿古拉斯流区,GOCE对应的相关系数高于GRACE对应的结果;而在黑潮区GOCE对应的相关系数与GRACE对应的结果接近;在赤道逆流区,GOCE对应的相关系数则低于GRACE对应的结果.参照纬度带的对比结果可知,在中高纬度区域,GOCE地转流场与浮标地转流场的空间分布有更好的一致性,在低纬度区域,GRACE地转流场与浮标地转流场的一致性更高.
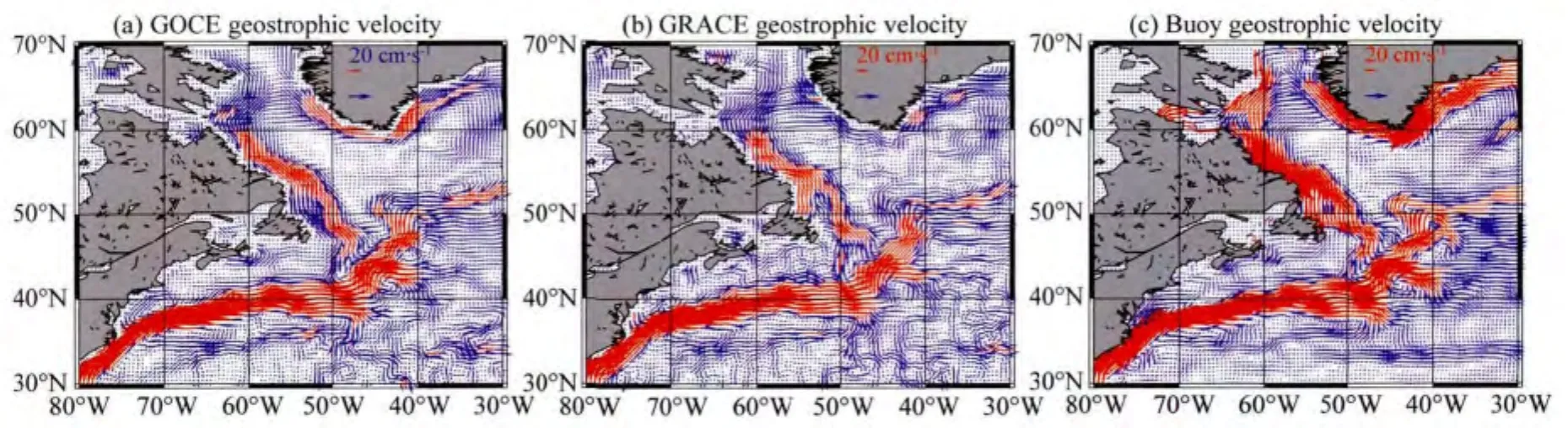
图6 北大西洋区域地转流对比,(a)、(b)、(c)分别为GOCE、GRACE和浮标得到的地转流场流速大于10cm/s的流速用红色箭头表示,其比例尺为右上角红色箭头;蓝色箭头表示流速小于10cm·s-1,比例尺为右上角蓝色箭头.Fig.6 Geostrophic currents derived from (a)GOCE gravity field,(b)GRACE gravity field,and(c)buoy Geostrophic current velocity larger(smaller)than 10cm·s-1 are shown in red(blue)arrow,note the different arrow scales were shown in the top right corner.

图7 地转流流速比.(a)和(b)分别为GOCE和GRACE得到地转流流速与浮标地转流流速的比例,(c)为GOCE与GRACE地转流流速之差与浮标地转流流速的比例Fig.7 Geostrophic currents speed proportion of(a)GOCE to buoy,(b)GRACE to buoy,and(c)difference between GOCE and GRACE(GOCE-GRACE)to buoy
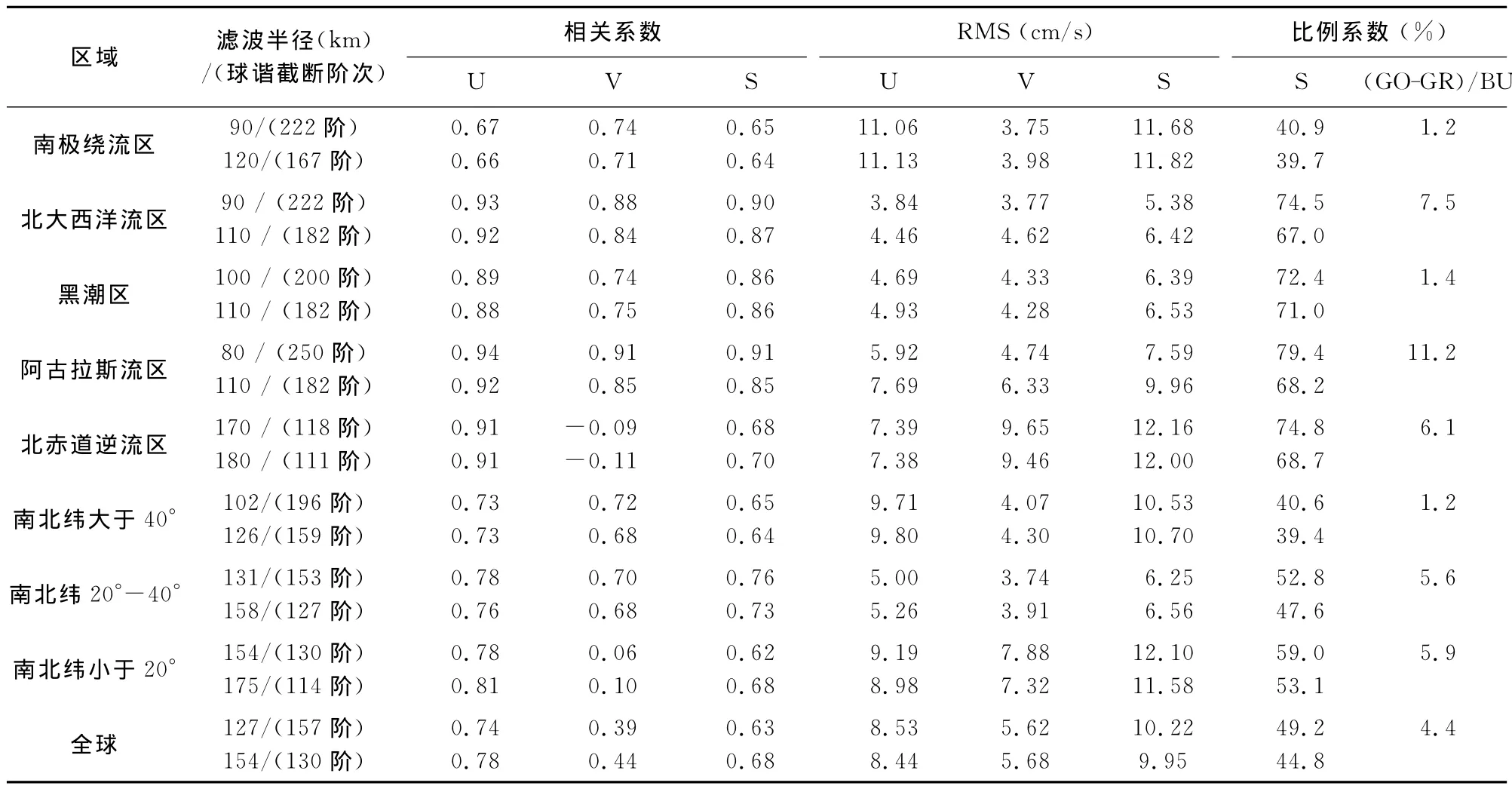
表1 滤波后海面动力地形对应的地转流场与浮标地转流场的对比Table 1 Comparison between geodetic and buoy geostrophic currents
(2)对比MDT得到的地转流场与浮标地转流场差异的均方根(RMS),可以发现,在强流区域,除了在北赤道逆流区域外,应用GOCE重力场的RMS均小于GRACE结果,其精度提高幅度从1%到24%不等;在北大西洋流区和阿古拉斯流区,相比于GRACE地转流,GOCE地转流精度的提高最明显,达到了16%和24%;对于纬度带的结果,在中高纬度(南北纬大于20°)区域,应用GOCE重力场的RMS低于GRACE结果,而在低纬度区域,应用GOCE重力场的RMS则略高于GRACE结果.无论是强流区域,还是纬度带结果都显示,在近赤道区域GOCE对应的地转流的精度低于GRACE对应地转流的精度,其原因是:在赤道区域,由于最优滤波半径明显大于其他区域,GOCE重力场高精度的高阶信号因滤波半径的加大而受到压制,从而削弱了其空间精度的提高,且经154km(GOCE)、175km(GRACE)的 滤 波 半 径 滤 波 后,GOCE/GRACE MDT对应的截断频率近似为130阶和114阶,参照图1可知,130阶处的GOCE重力场模型的大地水准面累积误差大于114阶处的GRACE重力场模型对应的大地水准面累积误差,而大地水准面误差又是MDT误差的主要组成部分.值得注意的是,不同区域的RMS并不能简单地直接比较,以用来区分不同区域的精度,这主要是因为在不同区域,浮标地转流场的高频信息是不一致的,而MDT得到的地转流场一般不包含这部分信息,此外我们选取的区域大小也是不一致的,因此这种意义下的RMS不能作为各个区域精度对比的衡量指标.
(3)从全球平均来看,GOCE地转流场与浮标地转流场的相关系数指标和RMS指标均劣于GRACE对应的指标,这一结果与Knudsen等(2011)的结论并不相符,其主要原因是采用了不同的重力场模型.如果采用与Knudsen(2011)一致的EIGEN4SGRACE模型,则我们的结果与其结论是一致的.对比Knudsen等(2011)采用的EIGEN4S模型与我们采用的ITG2010S模型的精度(图1),发现ITG2010S模型的精度在60阶以上高于EIGEN4S模型的精度,这说明我们的结论与Knudsen结果不完全一致的原因在于采用的GRACE对比模型的精度不同.我们还将Niller等(2003)计算的地转流场、Maximenko(2009)计算的地转流场分别作为对比对象,对比分析GOCE,GRACE地转流场的精度(图略),也得到了与本文一致的结论.因此,在全球尺度下,GOCE地转流对应的精度指标略低于GRACE对应的指标的结果是可信的.需要注意的是,这一结论是在GOCE地转流场比GRACE地转流场拥有更多细节信息的情况下得到的,其原因与较小的GOCE MDT滤波尺度有关,即较小的GOCE MDT滤波尺度使得更多的大地水准面误差和平均海面高度误差混入MDT中,深层原因仍有待于以后的进一步研究.
(4)除南极绕流区外,表1中的强流流轴区域,MDT得到的地转流场的流速约占浮标地转流场流速的67%~79%;且由GOCE得到的地转流场的流速相对于GRACE结果,普遍更接近浮标地转流场流速,其提高比为1%~11%.对于纬度带结果,则明显表现出从高向中低纬度,MDT得到的地转流速越来越接近浮标地转流速,但这种纬度平均意义的流速比,明显弱于强流区域的对应结果.对于南极绕流和黑潮区域,由GOCE得到的地转流与GRACE结果没有明显差异,说明在这两个区域,其他因素导致的误差,如复杂的浅海近岸地形(黑潮区),高频小尺度洋流和海面地形(南极绕流区)等,对地转流确定的影响是相对显著的,还需要做进一步的研究工作.
6 结论
本文利用卫星大地测量技术得到的GOCE和GRACE两种卫星重力场模型,卫星测高数据解算的海面高度场,采用频域法计算了MDT及其对应的地转流,并结合海洋表层漂流浮标的观测结果,对MDT的空间滤波尺度及其对应的地转流进行了分析.总体来讲,在获取MDT后,需要对其进行最优空间滤波,以控制信噪比,最大限度地提取信号和压制噪声.我们为此给出了区域、纬度带和全球最优滤波尺度因子.在强流区域,对MDT应用最优区域滤波尺度因子进行空间滤波,应用地转平衡公式求取地转流,得到了更高精度的地转流.通过与浮标地转流场的对比分析,发现在强流区域(南极绕流区域除外),采用MDT得到的地转流速可以解释观测浮标流速的70%,且二者具有明显的相关性.
对比由GOCE和GRACE重力场确定的MDT和地转流,可以发现,在全球区域,GOCE对应的MDT和地转流场在空间尺度上比GRACE对应的结果提高了27km;在中高纬度区域,相比于GRACE,GOCE得到的地转流的精度更高,其对应的地转流速在多个强流区域也有了明显提高;在近赤道的低纬度区域,GOCE得到的地转流的精度略低于GRACE对应的结果.
除此之外,我们还注意到,在诸如南极绕流和黑潮等强流区域,MDT得到的地转流与浮标地转流还是存在明显差异,而这种差异的来源,主要是观测误差和其他噪声信号的影响.为此,尝试结合多源海洋数据(如温盐数据、海表重力数据等),通过综合校正等提高浮标观测精度,进一步提高大地水准面的精度和空间分辨率等,都将有助于得到更高时空分辨率和高精度的MDT和地转流.
致谢 感谢德国地学中心(GFZ)、法国AVISO数据中心、美国国家海洋数据中心(NODC)提供数据资料;感谢欧空局(ESA)提供的GOCE User Toolbox软件;两位匿名审稿人的意见和建议提高了本文论证严密性,在此一并致谢.
Albertella A,Rummel R.2009.On the spectral consistency of the altimetric ocean and geoid surface:a one-dimensional example.Journal of Geodesy,83(9):805-815.
Albertella A,Savcenko R,Janjic′T,et al.2012.High resolution dynamic ocean topography in the Southern Ocean from GOCE.GeophysicalJournalInternational,190(2):922-930.
Albertella A,Wang X,Rummel R.2010.Filtering of altimetric sea surface heights with a global approach.∥Gravity,Geoid and Earth Observation.Berlin:Springer-Verlag,247-252.
Bingham R J,Haines K,Hughes C W,et al.2008.Calculating the ocean′s mean dynamic topography from a mean sea surface and a geoid.Journal of Atmospheric and Oceanic Technology,25(10):1808-1822.
Bingham R J,Knudsen P,Andersen O,et al.2011.An initial estimate of the North Atlantic steady-state geostrophic circulation from GOCE.Geophysical Research Letters,38(1),doi:10.1029/2010GL045633.
Brockmann J M,Zehentner N,Höck E,et al.2014.EGM_TIM_RL05:An independent geoid with centimeter accuracy purely based on the GOCE mission.Geophysical Research Letters,41(22):8089-8099.
Dibarboure G,Lauret O,Mertz F,et al.2008.SSALTO/DUACS user handbook:(M)SLA and(M)ADT near-real time and delayed time products.Rep.CLS-DOS-NT,6,39.
Farrell S L,McAdoo D C,Laxon S W,et al.2012.Mean dynamic topography of the Arctic Ocean.Geophysical Research Letters,39(1),doi:10.1029/2011GL050052.
Grodsky S A,Lumpkin R,Carton J A.2011.Spurious trends in global surface drifter currents.Geophysical Research Letters,38(10),doi:10.1029/2011GL047393.
Guan Z L,Guan Z,Zhai G J,et al.1996.Sea Surface Topography and Elevation Datum (in Chinese).Beijing:Surveying and Mapping Press.
Jekeli C.1981.Alternative methods to smooth the Earth′s gravity field.Report No.327.Columbus:Department of Geodetic Science and Surveying.The Ohio State University.
Knudsen P,Bingham R,Andersen O,et al.2011.A global mean dynamic topography and ocean circulation estimation using a preliminary GOCE gravity model.Journal of Geodesy,85(11):861-879.
Kalnay E,Kanamitsu M,Kistler R,et al.1996.The NCEP/NCAR 40-year reanalysis project.Bulletin of the American meteorological Society,77(3):437-471.
Li J C,Chen J Y,Ning J S,et al.2003.The Theory of Approaching Earth Gravity Field and Evaluation of Chinese 2000 Qusi-geoid(in Chinese).Wuhan:Wuhan University Press.
Lumpkin R,Pazos M.2007.Measuring surface currents with Surface Velocity Program drifters:the instrument,its data,and some recent results.∥Lagrangian Analysis and Prediction of Coastal and Ocean Dynamics.Cambridge:Cambridge University Press,39-67.
Maximenko N,Niiler P,Centurioni L,et al.2009.Mean dynamic topography of the ocean derived from satellite and drifting buoy data using three different techniques.Journal of Atmospheric and Oceanic Technology,26(9):1910-1919.
Mayer-Gürr T,Eicker A,Kurtenbach E,et al.2010.ITGGRACE:global static and temporal gravity field models from GRACE data.∥System Earth via Geodetic-Geophysical Space Techniques.Berlin:Springer Verlag,159-168.
Mulet S,Rio M H,Bingham R,et al.2011.An oceanographic assessment of the preliminary GOCE geoid models accuracy.∥4th International GOCE User Workshop,696:30.
Niiler P.2001.The world ocean surface circulation.International Geophysics,77:193-204.
Niiler P P,Maximenko N A,McWilliams J C.2003.Dynamically balanced absolute sea level of the global ocean derived from nearsurface velocity observations.Geophysical Research Letters,30(22),doi:10.1029/2003GL018628.
Niiler P P,Paduan J D.1995.Wind-driven motions in the northeast Pacific as measured by Lagrangian drifters.Journal of Physical Oceanography,25(11):2819-2830.
Pail R,Goiginger H,Mayrhofer R,et al.2010.GOCE gravity field model derived from orbit and gradiometry data applying the time-wise method.∥Proceedings of the ESA Living Planet Symposium(Vol.28).European Space Agency Bergen,Norway.
Pavlis N K,Holmes S A,Kenyon S C,et al.2011.The development and evaluation of the Earth Gravitational Model 2008 (EGM2008).Journal of Geophysical Research,117(B4):2156-2202.
Peng L F,Jiang W P,Jin T Y,et al.2013.The global mean dynamic topography and its corresponding sea surface geostrophic current derived from GOCE gravity field model.Acta Oceanologica Sinica (in Chinese),35(2):15-20.
Ralph E A,Niiler P P.1999.Wind-driven currents in the tropical Pacific.Journal of Physical Oceanography,29(9):2121-2129.
Rio M H,Guinehut S,Larnicol G.2011.New CNES-CLS09global mean dynamic topography computed from the combination of GRACE data,altimetry,and in situ measurements.Journal of Geophysical Research:Oceans(1978—2012),116(C7),doi:10.1029/2010JC006505.
Rio M H,Hernandez F.2004.A mean dynamic topography computed over the world ocean from altimetry,in situ measurements,and a geoid model.Journal of Geophysical Research:Oceans(1978—2012),109(C12),doi:10.1029/2003JC002226.
Rummel R.2010.GOCE:Gravitational Gradiometry in a Satellite.∥ Handbook of Geomathematics.Berlin:Springer-Verlag,93-103.
Rummel R,Yi W Y,Stummer C.2011.GOCE gravitational gradiometry.Journal of Geodesy,85(11):777-790.
Schaeffer P,Faugére Y,Legeais J F,et al.2012.The CNES_CLS11global mean sea surface computed from 16years of satellite Altimeter data.Marine Geodesy,35(S1):3-19.
Shi M C.2004.Physical Oceanography (in Chinese).Jinan:Shandong Education Press.
Wan X Y,Yu J H.2013.Mean dynamic topography calculated by GOCE gravity field model and CNES-CLS2010mean sea surface height.Chinese J.Geophys.(in Chinese),56(6):1850-1856,doi:10.6038/cjg20130607.
Wahr J,Molenaar M,Bryan F.1998.Time variability of the Earth′s gravity field:Hydrological and oceanic effects and their possible detection using GRACE.Journal of Geophysical Research:Solid Earth (1978—2012),103(B12):30205-30229.
Wahr J,Swenson S,Velicogna I.2006.Accuracy of GRACE mass estimates.Geophysical Research Letters,33(6),doi:10.1029/2005GL025305.
Yi W Y,Rummel R,Gruber T,et al.2013.Gravity field contribution analysis of GOCE gravitational gradient components.Studia Geophysica et Geodaetica,57(2):174-202.
Zhang Z Z,Lu Y.2005.Spectral analysis of quasi-stationary sea surface topography from GRACE mission.Science in China Series D:Earth Sciences,48(11):2040-2048.
Zhang Z Z,Lu Y,Xu H Z,et al.2007.Detecting surface geostrophic currents using wavelet filter from satellite geodesy.Science in China Series D:Earth Sciences,50(6):918-926.
附中文参考文献
管泽霖,管铮,翟国君等.1996.海面地形与高程基准.北京:测绘出版社.
李建成,陈俊勇,宁津生等.2003.地球重力场逼近理论与中国2000似大地水准面的确定.武汉:武汉大学出版社.
彭利峰,姜卫平,金涛勇等.2013.利用GOCE重力场模型确定全球稳态海面地形及表层地转流.海洋学报,35(2):15-20.
侍茂崇.2004.物理海洋学.济南:山东教育出版社.
万晓云,于锦海.2013.由GOCE引力场模型和CNES-CLS2010平均海面高计算的稳态海面地形.地球物理学报,56(6):1850-1856,doi:10.6038/cjg20130607.
张子占,陆洋.2005.GRACE卫星资料确定的稳态海面地形及其谱特征.中国科学D辑:地球科学,35(2):176-183.
张子占,陆洋,许厚泽等.2007.利用卫星测量技术和小波滤波方法探测表层地转流.中国科学D辑:地球科学,37(6):753-760.

