两种精化的对流层延迟改正模型
姚宜斌,张豹,严凤,许超钤
1 武汉大学测绘学院,武汉 430079
2 武汉大学地球空间环境与大地测量教育部重点实验室,武汉 430079
3 地球空间信息技术协同创新中心,武汉 430079
4 长江空间信息技术工程有限公司(武汉),武汉 430010
1 引言
GNSS信号穿越中性大气层时会产生时延和弯曲,导致接收机测距误差,这一误差我们称之为对流层延迟误差.对流层延迟是非色散性延迟,与信号频率无关,不能通过不同频率信号的线性组合予以消除,一般是采用模型进行改正.信号传播路径上的对流层延迟可以模型化为天顶方向的对流层延迟(Zenith Tropospheric Delay,ZTD)与投影函数(Mapping Function,MF)的乘积,而天顶对流层延迟又可以模型化为两部分:天顶静力学延迟(Zenith Hydrostatic Delay,ZHD)和天顶湿延迟(Zenith Wet Delay,ZWD),后者主要由水汽引起.传统的Hopfield模型(Hopfield,1971)、Saastamoinen模型(Saastamoinen,1972)和Black模型(Black,1978)都是基于理想气体状态方程和一些参数假设建立的,在有实测气象参数的条件下,天顶方向的改正精度为厘米级.Collins和Langley为美国的广域增强系统(Wide Area Augmentation System,WAAS)设计的无需实测气象参数支持的UNB系列(UNB1-4、UNB3m等)模型(Collins et al.,1996;Leandro et al.,2006),通过使用一个包含有温度、压强、水汽压(UNB3m为相对湿度)、温度垂直递减率、水汽垂直递减率的气象参数表来提供气象参数,进而利用Saastamoinen模型来计算天顶对流层延迟.其中广为使用的UNB3模型在无气象参数支持下其天顶方向对流层总延迟的预报精度为5.2cm,其改进型UNB3m模型的精度为4.9cm (Leandro et al.,2006).类似地,EGNOS模型是欧盟星基广域增强系统推荐用户使用的天顶对流层延迟改正模型(Penna et al.,2001),其形式与 UNB3模型相似,由于采用了简化公式,其精度略差于UNB3模型 (姚宜斌等,2013).UNB系列模型和EGNOS模型作为新一代对流层延迟模型,摆脱了对实测气象参数的依赖,但仍然可以取得与使用实测气象参数的传统对流层延迟模型相当的精度,极大地方便了用户的使用(曲伟箐等,2008).杨徉等(2013)利用 GPT模型给出的气温、气压以及UNB3m模型提供的水汽压参数作为Saastamoinen模型的输入参数构建了综合对流层延迟模型,该模型提高了Saastamoinen模型的适用性,但相比于UNB3m模型和EGNOS模型,精度并未有明显提升,其中可能的原因是依然沿用UNB3m模型中比较简单的相对湿度参数导致对流层延迟中的湿延迟成分估计不准.针对UNB系列模型、EGNOS模型等新一代对流层延迟模型中气象参数表过于简单、不能准确反映全球气象的不足,Li等直接对ZTD的时空特性建模,建立了复杂精致的IGGtrop模型 (Li et al.,2012),虽取得了良好的精度,但过于复杂的形式限制了它的使用.后来Li等发表了IGGtrop_ri(i=1,2,3)模型,新模型通过在赤道区域采用更为简洁的算法、在ZTD变化较小的区域采用较低的分辨率以及优化的参数存储方法等措施,使新模型的参数量显著减小,也使新模型更适用于BDS(BeiDou System)/GNSS研究和应用(Li et al.,2015).
总结前人的研究成果可以发现,经验化的对流层延迟模型主要有两种:一种是针对气象参数建模,然后利用物理方程计算天顶延迟量;另一种是直接对天顶延迟建模,不考虑气象参数.本文将分别采用这两种不同的思路建立时空分辨率接近的精致的对流层延迟模型,并评估这两种模型的优劣.
2 两种新的对流层延迟改正模型
2.1 GPT2+Saastamoinen模型
GPT2模型是基于 ERA-Interim (Dee et al.,2011)2001—2010年全球月平均的气压、气温、比湿的廓线资料建立的气象参数模型,它能以5°或1°的分辨率提供全球格网点上的气压、温度、温度垂直递减率、比湿以及 VMF1(Boehm et al.,2006)干湿投影函数的系数ah和aw(Lagler et al.,2013).在每个格网点上,每个气象参数r(t)的时间变化通过包含年周期和半年周期的三角函数表达(Lagler et al.,2013):
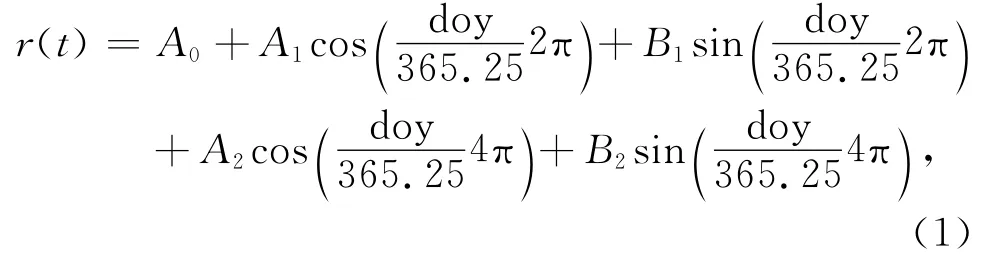
式中的A0,A1,A2,B1,B2都已事先计算好,并以格网形式保存在一个文本文件中.
在垂直方向上,Lagler等假定地球附近的温度随高度遵循线性变化,而气压的垂直变化则用指数函数来表达,并采用如下公式(http://ggosatm.hg.tuwien.ac.at/DELAY/SOURCE/gpt2.m)对气象参数进行高度改正(Lagler et al.,2013):
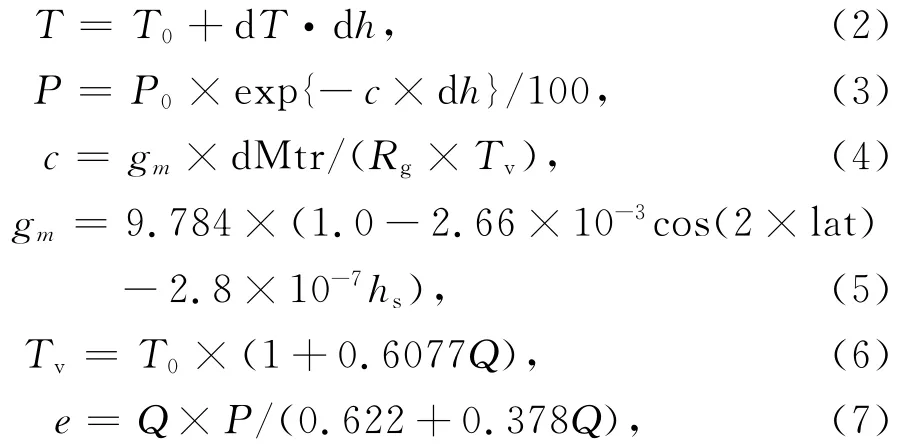
式中T0,P0分别是格网点上的气温(K)和气压(hPa),T和P分别是由格网点增加dh高度时的温度和气压,dT是温度的垂直递减率,Q是比湿,e是水汽压(hPa).gm为重力加速度,在GPT2模型中取值9.80665m·s-2.dMtr和Rg分别是大气摩尔质量和气体常数,其值分别为28.965×10-3kg/mol,8.3143J/K/mol.
当使用GPT2模型时,输入测站的纬度、经度、大地高以及观测时刻的约化儒略日,模型根据测站坐标查找格网文件中与之邻近的四个点,然后根据儒略日利用式(1)计算格网点上的气象参数,并利用式(2)—(7)将格网点上的气象参数归算到测站高度,最后利用双线性内插得出站点位置的气象参数.可考虑将使用GPT2模型计算的测站位置处的气象参数带入简化的Saastamoinen模型(李征航和黄劲松,2005)来计算测站位置处的天顶对流层延迟:
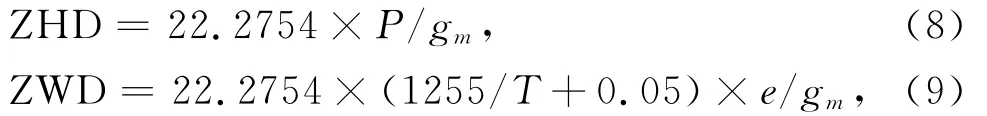
式中P和e的单位都是hPa,T的单位为K.至此,我们就可以利用GPT2模型和Saastamoinen模型来获取全球任意地点的天顶对流层延迟参数.为描述方便,以下将这种模型称为GPT2+Saas模型.
2.2 GZTDS模型
姚宜斌等(2013)建立了利用球谐函数表达的全球对流层天顶延迟模型GZTD.它首先将天顶对流层延迟参数表达为包含年周期和半年周期的三角函数,并使用指数函数进行高程改正,其形式可如下表达:
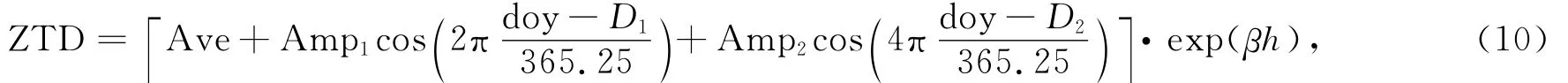
式中ZTD表示天顶总延迟,Ave为ZTD的年均值,Amp1为ZTD年周期项的振幅,Amp2为半年周期项的振幅,D1和D2分别为年周期和半年周期的初始相位,h为测站高程,β为高程改正系数,全球取平均值-1.3137×10-4(姚宜斌等,2013).式(10)的表达方法与式(1)是等价的.为使用的方便,再利用10×10阶球谐函数对模型系数进行拟合.
GPT2模型是利用2001—2010年共10年的ECMWF (European Centre for Medium-range Weather Forecast)ERA-Interim月平均的气压、气温、比湿和位势等气象数据来求解式(1)中气象参数的系数,并在全球范围内以1°和5°的分辨率提供了GPT2模型参数表(ASCII格式的1°文件为14MB,5°为0.5MB)(Lagler et al.,2013).GGOS Atmosphere提供的ZHD和ZWD也是以ECMWF的再分析资料为基础计算的,但它以纬度2°经度2.5°的分辨率提供每天0∶00,6∶00,12∶00和18∶00UTC的格网产品.在本文的研究中,为了最大程度地使新GZTD模型与GPT2模型(5°分辨率的)保持一致(因为2.1中的模型将基于 GPT2),我们利用 GGOS Atmosphere 2001—2010年的ZHD和ZWD数据在4°×5°(纬度每隔4°,经度每隔5°)的格网点上拟合(10)式中的ZTD模型系数 Ave、Amp1、Amp2、D1和D2,并不再用球谐函数进行表达,而直接以文本形式存储这些格网点上的模型系数信息,由此确立的新模型我们称之为GZTDS(分辨率为纬度方向4°,经度方向5°).这样确立的GZTDS模型无论在建模数据源上还是在模型的分辨率上都最大程度地与GPT2+Saas模型保持了一致性,这样更有利于对两种建模方式本身进行更客观的评估.当使用GZTDS模型时,首先根据测站经纬度找到与之邻近的四个格网点,然后根据公式(10)和模型系数分别计算四个格网点上相对于测站高度的ZTD,最后利用双线性内插法计算测站位置处的ZTD.
3 模型验证
3.1 利用GGOS Atmosphere格网数据对模型进行验证
为了验证两种不同建模方法的正确性和有效性,我们将2011—2013年的GGOS Atmosphere提供的天顶对流层延迟数据作为参考值,对GPT2+Saas模型和GZTDS模型进行了检验,并与新一代经验模型(这里指UNB系列模型和EGNOS模型)中表现最好的UNB3m模型和先前建立的GZTD模型进行了比较.在每个格网点上(纬度方向每隔4°,经度方向每隔5°)我们统计了模型相对于参考值的平均偏差(Bias)和均方根误差(RMS),图1给出了四种模型的Bias和RMS在全球的分布情况.
由图1a可以看出UNB3m模型在南极和赤道附近地区存在较大的Bias和RMS,其精度的地理分布非常不均匀,北半球的精度明显优于南半球.导致这种情况的原因是UNB3m的气象参数表过于简单,它每隔15纬度才提供5个气象参数的均值和振幅,且不考虑气象参数的经向变化,并且基于对称假设简单地将南半球取与北半球相同的气象参数,仅仅将振幅的符号改变,这样导致模型在南半球精度很差,尤其是在南半球高纬度地区.图1b中的GPT2+Saas模型明显优于UNB3m模型,其精度的地理分布更为均匀,但在赤道地区仍然存在精度较差的情况.比较图1c和1d可以看出,GZTDS模型在全球范围内的精度分布要优于GZTD模型,尤其是削弱了GZTD模型在中低纬度的误差,这主要与采用格网模型代替球谐拟合有关,因为直接用格网方法给出每个点上的模型系数相对于球谐函数拟合,避免了拟合误差的引入,同时也保留了原有的分辨率,缺点仅仅是保留了原始的数量较多的参数,同时更长时间跨度的数据(GZTD模型8年数据,GZTDS模型10年数据)被用于拟合模型也有利于提高模型精度.图1d中的GZTDS模型相比GPT2+Saas模型有了进一步的改进,尤其是显著消除了模型在全球范围内的偏差,模型精度有所提高,精度的地理分布也更为一致.表1统计了四种模型在2011—2013年里的平均Bias和平均RMS,由此可以更加准确地看出模型的整体精度情况.

表1 利用2011—2013年的GGOS Atmosphere数据对四种模型的检验结果(单位:cm)Table 1 Test results of the four models from 2011to 2013 with respect to GGOS Atmosphere data(unit:cm)
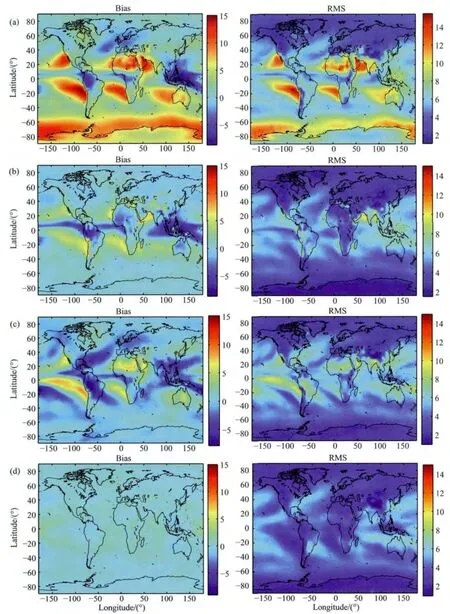
图1 相对于2011—2013年GGOS Atmosphere的ZTD数据,四种模型在全球的Bias和RMS分布(单位:cm)(根据4°×5°的检验结果画出)(a)UNB3m;(b)GPT2+Saas;(c)GZTD;(d)GZTDS.Fig.1 Global Bias and RMS(in cm)with respect to GGOS Atmosphere ZTD data from 2011to 2013for the four models(the resolution of results is 4°×5°)
表1显示了四种模型在2011—2013年的精度信息,可以看出四种模型在任意1年或3年里的精度都是非常稳定的.表现最优的是GZTDS模型,其平均偏差仅为0.2cm,平均RMS为3.7cm,相对于GZTD模型精度提高了0.6cm;其次为GPT2+Saas模型,最差的是UNB3m模型.需要指出的是UNB3m模型显示了一个较大的平均偏差(~3.4cm),这可能是因为用于建模的数据集与参与检验的数据集存在系统差导致的,在3.2节我们将利用IGS提供的GNSS实测对流层延迟数据对这四种模型进行检验.
上面对四种模型的精度进行了检验,并给出了模型精度的地理分布情况,这里我们进一步对模型的季节变化进行研究分析.由于季节受纬度影响,我们将同一纬度不同格网点同一天的数据取平均,并在同一纬度上比较四种模型的表现,这样可以有效消除纬度对季节变化的影响.我们在高中低纬分别选择了一特定纬度作为代表,统计了2011—2013年四种模型在6条纬线上的季节变化,并将GGOS Atmosphere的ZTD数据作为参照,结果如图2所示.
由图2a和2b可以看出ZTD在低纬度地区的值较大,高纬度地区的值较小,这主要由于水汽的纬度差异导致的,即低纬度地区水汽含量丰富,对湿延迟的贡献较大,而高纬度地区水汽含量较低,对湿延迟贡献较小.与参考ZTD值相比,GZTDS模型与参考值最吻合,GPT2+Saas模型略差于GZTDS模型,而UNB3m模型表现较差,GZTD模型的变化趋势与GZTDS模型比较接近.GZTDS模型和GPT2+Saas模型在不同纬度既可以表现ZTD变化的年周期特性(如38°N,70°N,6°S,38°S),又能表现其半年周期特性(如6°N,70°S),而UNB3m模型至多只能表现年周期特性,在低于15°的纬度区间里,其ZTD不再表现时间变化.比较图2a和2b中三条纬度线的分布,可以明显看出ZTD并不具备南北半球对称的特性,因此,UNB系列模型和EGNOS模型中假定南北半球对称的做法是不准确的.以上种种表明GZTDS模型和GPT2+Saas模型相对于UNB系列模型和EGNOS模型更加精致,精度和稳定性更高,是两种具有可用性的不同类型(以Saastamoinen模型中物理方程为基础的模型和纯以ZTD统计性质为基础的模型)的精化对流层延迟经验模型.
3.2 利用IGS实测数据对模型进行验证
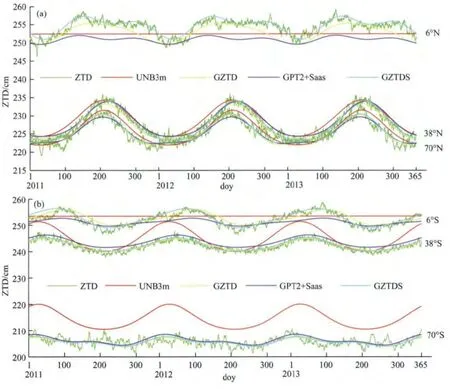
图2 四种模型2011—2013年在6条纬度线上的季节变化,参考值为GGOS Atmosphere的ZTD数据,图中用ZTD表示(a)和(b)分别显示的是模型在北半球和南半球高中低三条纬线上的ZTD.Fig.2 Seasonal variations of the four models at 6latitudes from 2011to 2013with respect to GGOS Atmosphere ZTD data which is labeled as ZTD in the figure(a)and(b)show respectively the ZTD at high,middle,low latitudes in the north and south hemisphere.
由于GGOS Atmosphere的数据可能与构建UNB3m模型的数据存在系统性偏差,因此3.1节中的结果可能不能完全准确地反映UNB3m模型的效能.为此,我们将2010年全年123个IGS站上的ZTD数据作为参考值,对以上四种模型重新进行了检验,同样统计了每个测站上模型值与参考值的平均Bias和RMS.图3按纬度显示的是123个测站上的平均Bias和RMS,表2统计了四种模型的平均Bias和RMS.

表2 利用2010年123个IGS站的ZTD数据对四种模型的检验结果(单位:cm)Table 2 Test results of the four models with respect to the ZTD data from 123IGS stations in 2010(unit:cm)
图3显示了四种模型的Bias和RMS随纬度的变化情况,可以明显看到GZTDS模型在各个纬度的精度比较平稳,波动不大,GZTD模型与之相似;而UNB3m模型和GPT2+Saas模型的精度在不同纬度都出现了较大的波动.与采用GGOS Atmosphere格网数据检验的结果类似,UNB3m模型在南半球的精度要明显差于北半球,这与它的球对称假设有关;GPT2+Saas模型主要在20°N—30°N之间出现了三个误差较大的站点(KOKV、LPAL和MAUI),这三个站都分布在水汽丰富且高程超过1100m的地方,高程改正和水汽估计效能不佳可能是导致GPT2+Saas模型出现较大误差的原因.表2中的整体统计结果显示GZTDS模型表现出了与3.1节中采用GGOS Atmosphere格网数据进行检验非常近似的精度,精度依然比GZTD提升了0.6cm;GPT2+Saas模型精度有所下降,UNB3m模型的精度却有所提升.相对于UNB3m模型,GPT2+Saas模型精度提升10%,GZTD模型精度提升15%,GZTDS模型的精度提升了27%.鉴于这四种模型都是为导航定位服务,因此采用IGS数据对其进行的检验更客观,也更具参考价值.
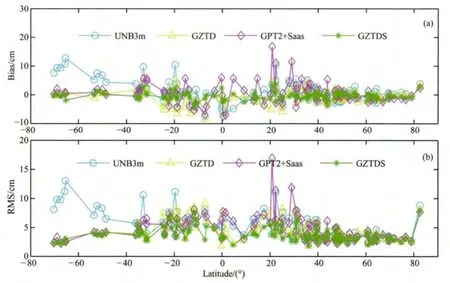
图3 利用123个IGS站2010年的数据对四种模型的检验Fig.3 Test results of the four models with respect to the ZTD data from 123IGS stations in 2010
为了找出图3中GPT2+Saas模型在三个站点误差较大的原因,我们给出了模型精度随高程的变化曲线,如图4所示.
在图4中品红色曲线上数值最大的三个点即是KOKV (RMS:11.4cm)、LPAL(RMS:11.9cm)和 MAUI(RMS:16.9cm)测站上的检验结果.尽管这三个点位于高程较高的区间,但其邻近高程的其他点并未出现误差大于10cm的情况,并且除了这三个点整条曲线的波动并不大,这说明GPT2+Saas模型在这三个站出现较大误差的原因并不是高程改正不好.由于GZTDS的模型值与GGOS的ZTD数据和IGS的ZTD数据都能很好吻合,这又排除了ZTD数据质量不好的可能,故更可能的原因是GPT2模型不能很好地反映这三处气象元素的实际变化规律,进而导致Saastamoinen模型计算ZTD不准确.通过图4也可以看出UNB3m模型在低高程区间的改正效果要差于在高高程区间的改正效果,这与我们之前的研究结果吻合.GZTDS模型在各高程区间表现非常平稳,且精度也明显优于UNB3m模型和GPT2+Saas模型,这进一步证实了GZTDS模型的优良性能.
为了确定GPT2+Saas模型在三个点出现大误差的原因,我们利用2010年ECMWF的地表温度、气压和水汽压的格网数据,按照式(2)—(7)的方法将测站邻近四个格网点的气象数据改正到测站高度,然后利用双线性内插法得到测站位置处的温度、气压和水汽压,并与GPT2模型给出的结果进行比较,图5显示的是KOKV站上的ECMWF数据与GPT2数据对比曲线.
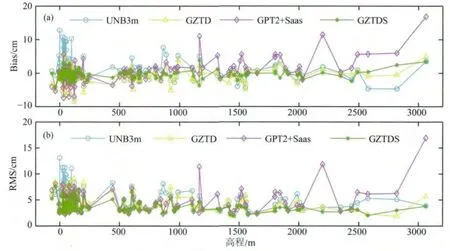
图4 利用123个IGS站数据对四种模型的检验结果与高程的关系Fig.4 The relationship between the accuracy and the height from the test results with respect to the 123IGS stations
由图5可以粗略地看出来自GPT2的气象数据曲线基本表征了ECMWF数据的变化规律,其他两个测站上也出现了近似的情况.表3统计了三个测站上对应气象数据较差(ECMWF-GPT2)的RMS.
对式(8)和式(9)取一阶导数可以更好地显示天顶延迟误差与气象误差之间的关系,重力加速度近似值取9.80665m·s-2,温度近似值取280K,水汽压近似值取10hPa,可得:

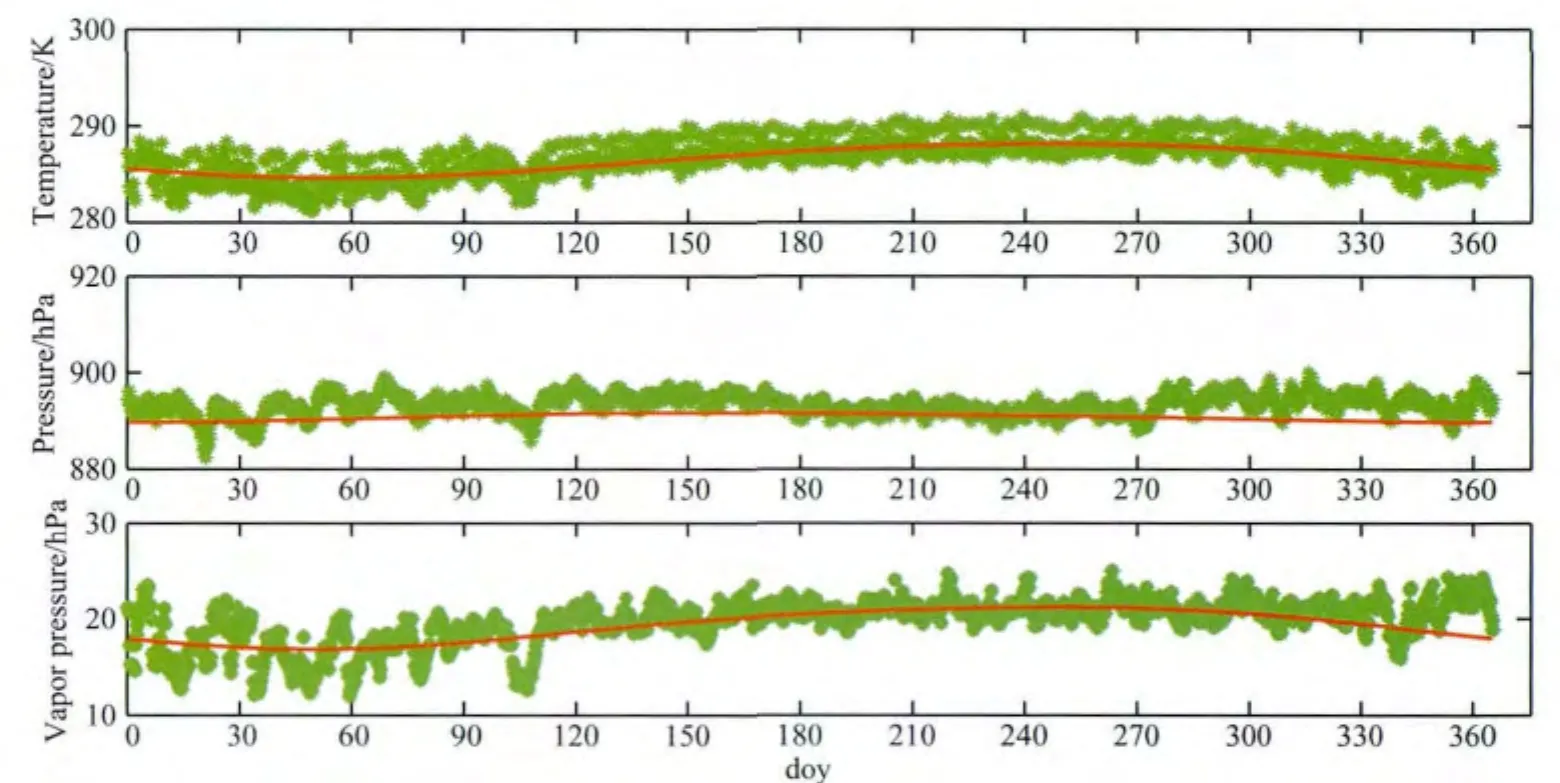
图5 来自ECMWF的KOKV测站上的地表温度、气压、水汽压与对应的来自GPT2模型的数据的比较(ECMWF数据用绿色曲线表示,GPT2模型的数据用红色曲线表示)Fig.5 Comparisons between temperature,pressure and vapor pressure from ECMWF data and that from GPT2model at IGS site KOKV (green curve represents ECMWF data and red curve represents data from GPT2model)
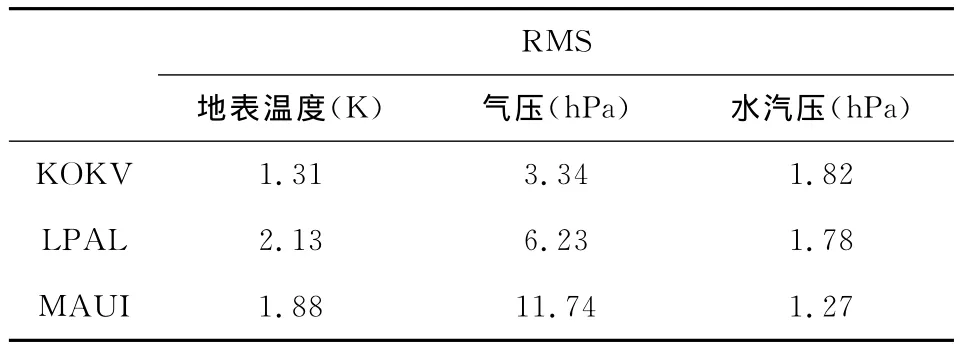
表3 KOKV、LPAL和MAUI站上GPT2模型值相对于ECMWF气象数据的RMSTable 3 RMS of GPT2model with respect to the ECMWF data at IGS site KOKV,LPAL and MAUI
δZWD=-0.16δT+4.53δe, (12)式(11)、(12)中的δZHD和δZWD的单位都是mm.将误差传播率应用于式(11)和式(12)并带入表3中的误差参数可以算出KOKV、LPAL、MAUI站上的气象误差分别可引起1.1cm,1.6cm和2.7cm的ZTD估计误差,这并不会导致GPT2+Saas模型产生超过10cm的误差.为了找到原因,我们直接利用这三个点邻近四个格网点上的ECMWF气象数据来计算ZTD,然后与直接来自GGOS Atmosphere的数据进行比对.分别计算了三个测站邻近四个格网点上Saastamoinen模型利用ECMWF数据计算的ZTD与GGOS Atmosphere的ZTD的差值的平均RMS,结果显示KOKV、LPAL、MAUI三个站邻近四个格网点的平均RMS分别为5.5cm,6.8cm和9.0cm,计算值与实测值差值较大,由于Saastamoinen模型本身具有较高的精度,这说明ECMWF气象数据本身在这三个点精度较差是导致二者差别较大的原因.考虑到GPT2经验气象参数相对ECMWF数据的差异又可引起1.1cm,1.6cm 和2.7cm 的ZTD估计误差以及超过1km的高程归化和平面内插等引起的误差,导致上述三个点产生超过10cm的误差是非常可能的,其中的主要原因应该是ECMWF数据在这三个点质量不佳.
4 结论
遵循传统对流层建模思路,我们利用GPT2模型来提供温度、气压和水汽压等气象参数,然后将这些参数带入Saastamoinen模型计算天顶对流层延迟,据此建立了精化的GPT2+Saas模型.采用新的对流层建模思路,我们直接针对ZTD的时空特性建模,利用GGOS Atmosphere 2001—2010年的数据直接构造了GZTDS格网模型.利用GGOS Atmosphere的格网数据对两种新模型进行了检验,并与UNB3m模型和GZTD模型进行了比较,给出了四种模型精度的时空分布,结果表明两种新模型的对流层延迟估计精度均明显优于UNB3m模型,其中GZTDS模型表现出最佳的精度和稳定性.利用IGS的ZTD数据对新模型进行检验,给出了客观实用的精度信息,相对于UNB3m模型,GPT2+Saas模型精度提升10%,GZTD模型精度提升15%,GZTDS模型精度提升27%,GPT2+Saas模型和GZTDS模型的高程改正效果也要优于UNB3m模型.针对GPT2+Saas模型在三个IGS站出现较大误差的情况,我们进行了深入分析研究,确定了ECMWF气象数据在这三点的质量不佳是导致误差较大的主要原因.
严格的检验证实:直接对对流层延迟进行建模是一种可行且可靠的思路,相对于传统的建模思路,它更加简便并且精度和可靠性也表现出了优于同等传统模型的潜力,是一种值得推广的方法.
致谢 感谢ECMWF提供的气象数据、IGS提供的ZTD数据以及GGOS Atmosphere提供的ZTD数据.
Black H D.1978. An easily implemented algorithm for the tropospheric range correction.JournalofGeophysicalResearch:SolidEarth(1978—2012),83(B4):1825-1828.
Boehm J,Werl B,Schuh H.2006.Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data.JournalofGeophysicalResearch,111(B2),doi:10.1029/2005JB003629.
Collins P,Langley R,LaMance J.1996.Limiting factors in tropospheric propagation delay error modelling for GPS airborne navigation.//Proceedings of the Institute of Navigation 52nd Annual Meeting.Cambridge,MA,USA,519-528.
Dee D P,Uppala S M,Simmons A J,et al.2011.The ERA-Interim reanalysis:Configuration and performance of the data assimilation system.QuarterlyJournaloftheRoyalMeteorologicalSociety,137(656):553-597,doi:10.1002/qj.828.
Hopfield H S.1971.Tropospheric effect on electromagnetically measured range:prediction from surface weather data.Radio Science,6(3):357-367.doi:10.1029/RS006i003p00357.
Lagler K,Schindelegger M,Böhm J,et al.2013.GPT2:Empirical slant delay model for radio space geodetic techniques.GeophysicalResearchLetters,40(6):1069-1073,doi:10.1002/grl.50288.
Leandro R,Santos M C,Langley R B.2006.UNB neutral atmosphere models:development and performance.//Proceedings of the ION NTM 2006Monterey,California,USA,564-573.
Li W,Yuan Y B,Ou J K,et al.2012.A new global zenith tropospheric delay model IGGtrop for GNSS applications.Chinese Science Bulletin,57(17):2132-2139,doi:10.1007/s11434-012-5010-9.
Li W,Yuan Y B,Ou J K,et al.2015.New versions of the BDS/GNSS zenith tropospheric delay model IGGtrop.Journal of Geodesy,89(1):73-80.
Li Z,Huang J S.2005.GPS Surveying and Data Processing(in Chinese).Wuchang:Wuhan University Press,66-68.
Penna N,Dodson A,Chen W.2001.Assessment of EGNOS tropospheric correction model.The Journal of Navigation,54(1):37-55.
Qu W J,Zhu W Y,Song S L,et al.2008.The evaluation of precision about Hopfield,Saastamoinen and EGNOS tropospheric delay correction model.Acta Astronomica Sinica (in Chinese),49(1):113-122.
Saastamoinen J.1972.Introduction to practical computation of astronomical refraction.Bulletin Géodésique,106(1):383-397.Yao Y B,He C Y,Zhang B,et al.2013.A new global zenith tropospheric delay model GZTD.Chinese Journal of Geophysics
(in Chinese),56(7):2219-2227,doi:10.6038/cjg20130709.Yang Y,Yu G R,Pan S G,et al.2013.A comprehensive algorithm
using fusion of tropospheric delay models.Journal of Southeast University (Nature Science Edition)(in Chinese),43(Suppl.II):419-422,doi:10.3969/j.issn.1001-0505.2013.S2.043.
附中文参考文献
李征航,黄劲松.2005.GPS测量与数据处理.武昌:武汉大学出版社,66-68.
曲伟箐,朱文耀,宋淑丽等.2008.三种对流层延迟改正模型精度评估.天文学报,49(1):113-122.
姚宜斌,何畅勇,张豹等.2013.一种新的全球对流层天顶延迟模型GZTD.地球物理学报,56(7):2219-2227,doi:10.6038/cjg20130709.
杨徉,喻国荣,潘树国等.2013.一种综合的对流层延迟模型算法.东南大学学报(自然科学版),43(增刊II):419-422,doi:10.3969/j.issn.1001-0505.2013.S2.043.
——环地平弧&环天顶弧

