位涡塔结构及演变对飓风Wilma(2005)强度变化的影响
刘爽,钟玮,刘继晨,陆汉城
中国人民解放军理工大学气象海洋学院,南京 211101
1 引言
热带气旋(Tropical Cyclone:TC)结构和强度突变机理是当前热带气旋预报存在的主要难题(陈联寿等,2002),也是动力学研究的重要关注领域.影响热带气旋结构和强度的变化因子可以分为两类,即外部大尺度环境强迫因子和热带气旋内部扰动变化(Wang and Wu,2004).研究表明,大尺度环境因子如环境风垂直切变(Bender,1997;Holland and Wang,1999)、海表面温度及其与大气的相互作用(Duan et al.,1998)、边界层动力和热力因子(陈联寿和丁一汇,1979;Bender et al.,1993)等在热带气旋强度和结构突变过程中具有重要作用.近年来,一系列热带气旋动力学研究进展也加深了我们对涡旋内部非对称结构形成和传播的波动特征(Montgomery and Kallenbach 1997,Zhong et al.,2009)、多边形眼墙(Schubert et al.,1999;Montgomery et al.,2002)、眼墙替换过程(Houze et al.,2007;Terwey and Montgomery,2008)等内部物理过程的认识和理解.观测研究也表明,这些内部过程与热带气旋系统强度和结构的突然变化密切相关(Montgomery et al.,2006;Aberson et al.,2006),但是由于缺乏对这些物理过程的整体认识,这些内部动力学过程对热带气旋强度和结构突变影响的物理机制还不清楚(Wang and Wu,2004).
最新观测和模拟研究揭示,热带气旋内核区域存在高值位涡(Potential Vorticity:PV)区.这类高值位涡的大值中心在水平分布上一般位于眼心或眼墙内侧,在垂直方向上相应地表现为高值PV柱状结构,可称为“PV 塔”(PV tower:PVT)(Schubert and Alworth,1987;Möller and Smith,1994).已有研究表明,PVT径向结构主要具有两类基本特征:①PV大值区位于眼心并沿径向方向向外递减,表现为单极分布特征;②PV大值区位于眼墙内侧,并向眼心和外侧双向递减,此时等PV面眼心区出现漏斗状的下凹特征,说明PV廓线具有中空特征.根据PV的径向分布,将三维PVT分别定义为单极位涡塔(Monopole PVT:MPVT)和中空位涡塔(Hollow PVT:HPVT).
PV径向分布差异是影响热带气旋动力稳定性的重要因子.Nolan等(2001)提出,除眼心外基流绝对涡度在眼墙内侧出现的极值点会导致基态涡旋出现代数不稳定增长;Zhong等(2010)认为,在眼心到边界半径的开区间范围内,存在一个使得基流绝对涡度的径向梯度为零值的点是涡旋Rossby波正压不稳定存在的必要条件之一;Zhong等(2009)提出,在强旋转和强涡旋共存条件下,在高波数、大Rossby数以及环境风场存在强的径向二次切变时,容易出现重力波和涡旋Rossby波物理性质不可分的混合波和混合波不稳定.由此可见,PV的径向分布差异是决定热带气旋涡旋系统稳定性的重要因子.Hendrick(2008)基于正压涡度守恒方程理想模型中的涡度径向分布特征,分别讨论了在MPVT和HPVT不同结构条件下,PV的混合和输送过程及其对基态涡旋动力稳定性的影响.同样,利用理论模型,Hendrick(2008)、Hendrick和Schubert(2010)讨论了不同强度和不同厚度的HPVT对基态涡旋的演变特征的影响,分析得到了PV输送和混合作用下,基态涡旋中心气压和最大风速的变化情况,揭示了PVT分布特征对基态涡旋结构和强度变化的影响.
目前对于MPVT以及HPVT对热带气旋动力稳定性以及热带气旋强度变化的影响研究,主要基于简单数值模型的理想试验,为了进一步理解PVT在实际热带气旋变化过程中的影响和作用,本文利用高分辨率数值模拟资料,对具有快速增强(Rapid Intensification:RI)过程的飓风 Wilma(2005)进行诊断分析.第二节中利用模拟资料,在对 Wilma(2005)强度和结构的变化特征诊断基础上,分析了暖心、凝结潜热和低层动力稳定性作用下位涡与强度变化的关系;第三节根据飓风发展不同阶段PVT的结构分析,追踪实际飓风个例中PVT的分布和演变特征对飓风强度和结构突变的影响过程,揭示了PV三维结构变化对飓风强度突然变化的指示意义;在第四节中,引入HPVT结构参数的定量分析,诊断不同阶段HPVT稳定度的大小,反映PVT结构对基态涡旋系统稳定度的影响,探讨HPVT的建立和崩溃对飓风强度突变的影响.最后是结论与讨论部分.
2 位涡与飓风Wilma(2005)的强度和结构变化
飓风Wilma(2005)是有记录以来发生在大西洋上强度最强的热带气旋,其发生发展过程伴随的强风、暴雨和风暴潮在墨西哥和美国造成了重大的人员伤亡和经济损失.Chen等(2011)利用 WRF模式,采用4层双向嵌套网格,对其进行了数值模拟,模拟时间为2005年10月18日00时—21日00时(世界时),共72小时.空间分辨率达到1km,输出时间精度达到5min.这次模拟很好地再现了Wilma(2005)发展过程的三个特点:破纪录的快速增强过程,极端的超级强度和极小的眼心尺度,以及典型的眼墙收缩和替换过程(Chen等,2011).
参照Chen等(2011)的划分标准,根据 Wilma(2005)最低海平面气压Pmin和最大地面风速Umax分布(图1a),可以将模拟过程分为快速增强前(pre-RI)阶段(积分0—15时,18日00时—15时,共15h)、快速增强(RI)阶段(积分15—36时,18日15时—19日12时,共21h)和快速增长后(post-RI)阶段(积分36—72时,19日12时—21日00时,共36h).
结合Pmin和Vmax的每小时变化(图1b)可以看出,除去模式初始6小时的强度调整外,pre-RI阶段Pmin每小时平均变化率均小于4hPa,而Vmax的个别时次每小时变化量值虽然较大,但存在正负交替振荡分布的特征,说明系统整体是平稳增强的.到RI阶段,Pmin和Vmax的每小时变化明显增大,平均变化率分别达到3.44hPa·h-1和1.0m·s-1·h-1,最大变化值超过6.48hPa·h-1和6.12m·s-1·h-1,模式试验很好地再现了 Wilma的快速增强过程.另外从Pmin和Vmax变化情况来看,RI阶段也存在两个时期:一是RI过程的前12h(即积分15—27时),系统出现爆发性增强,Pmin的平均变化率达到4.58hPa·h-1,相对应的Vmax的平均变化率也超过1.85m·s-1·h-1;二是RI过程的后9h(即积分27—36时),系统增强的速率迅速减小,Pmin平均每小时降低1.93hPa,Vmax的平均变化率仅为0.12m·s-1·h-1,逐渐向强度减弱期过渡.
位涡是一个既包含热力因子又包含动力因子的综合物理量,具有严格的守恒性和可反演性,该物理量有助于加深我们对热带气旋内部动力学过程的认识和理解.本文采用一般形式的Ertel位涡作为研究对象,其计算表达式为
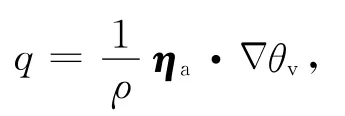
为了描述飓风Wilma(2005)强度变化过程中位涡及其相关物理量随时间的演变特征,考虑到Wilma的尺度特征,绘制飓风内核区域(60km×60km)平均位涡距平和非绝热加热率、眼心处温度距平和位温随时间变化的剖面图(图1c).图中将当前时刻的位涡(温度)与积分初始时刻内核区域(60km×60km)的位涡(温度)平均值之差定义为该时刻的位涡(温度)距平,由图可见区域平均位涡距平随时间分布的特点,正位涡异常的大值中心主要集中在三个高度区域,分别在16km左右的对流层高层、从5km高度延伸至12km的对流层中层和3km左右的低层.在积分初始时刻,伴随着等位温线由高层向低层倾斜和高层暖心下传,飓风内核区域出现了位于16km高度的正位涡异常,并一直维持到飓风最强时刻.进入RI阶段后,等位温线下降坡度变陡,高层暖心开始分裂为两个,中心分别位于16km以上和13km高度.此时,高层垂直位温梯度开始减小,位涡正异常逐渐减弱.到积分36小时以后,等位温线趋于平直,温度梯度变化不大,位涡正异常信号消失.Chen和Zhang(2013)分析垂直暖心结构随时间变化时指出,370~400K的等位温面下降和平流层低层的下沉运动,是造成飓风发展阶段高层暖心增强的主要原因.而高层暖心的增强和下传也导致了飓风内核区域平均高层位涡的增大.中层和低层的正位涡异常与相应层次上凝结潜热引起的非绝热加热大值区一致.由于对流启动后中层凝结释放较早,因此中层位涡正异常的出现较低层的略早1小时,并在凝结潜热加热率增大和暖心下传的共同作用下迅速增强.尤其是进入RI阶段后,中层非绝热加热率由10K/h快速增加,在积分27h左右非绝热加热率达到最大,超过25K/h,这一时期对应的中层位涡正异常急剧增加,到积分27h时,中层位涡正异常超过21PVU.随后,尽管中层位涡正异常仍然呈增长趋势,在积分36h时达到最强,整个区域位涡增大超过24PVU,但随着非绝热加热率开始减小,中层位涡正异常增长的幅度也跟着减小.对照飓风Wilma在RI过程中的强度变化(图1b)来看,RI过程的后9h(即积分27—36时),系统增强的速率迅速减小.可以看出,中层的正位涡异常是与凝结潜热释放密切联系的.随后,中层位涡的强度和垂直伸展高度均明显减小,飓风也进入减弱阶段.低层位涡的快速增长期也与RI阶段一致,虽然其增长速率和强度均小于中层的,但进入post-RI阶段,相比中层位涡的迅速减小,低层位涡强度则较为稳定,到积分70小时后,位涡正异常又再次出现增强.低层位涡存在较强的非绝热加热区,其强度变化一定程度上受到非绝热加热影响,同时也和眼心处由于强静力稳定造成的逆温层以及内核区动力不稳定引起的PV混合有关(Hendricks and Schubert,2010).
为了进一步讨论飓风内核区域动力过程作用下低层位涡结构与飓风结构和强度突然变化的关系,考虑到模式调整时间,本文选取了Wilma发展阶段(积分6—36小时)3km高度上切向平均雷达反射率和切向平均位涡随时间的演变(图2).可以看出在pre-RI阶段,飓风内部对流较弱,对流分布较为零散,此时位涡在径向分布上表现为单极分布特征,即位涡的最大值位于眼心,沿着半径增大的方向单调递减.进入RI阶段后,整个区域的位涡明显增强,此时位涡的径向结构变为中空特征,即位涡的最大值点从眼心处逐渐外移,且最大值点与眼心之间区域的位涡径向梯度也明显增大.此外,积分13小时后对流组织化,形成典型的眼墙和螺旋雨带结构,而与眼墙相对应的最强回波区内侧也出现了位涡的次大值点,伴随着眼墙的半径从20km快速向内收缩到10km左右;积分24个小时后,它与位涡最大值点合并;到积分31小时左右时,位涡最大值点的量值以及与眼心的径向梯度均达到最强.因而,模式试验结果表明位涡的径向结构由单极分布转变为中空特征,根据已有的理论分析,切向平均位涡的中空径向分布特征是基态涡旋系统出现动力不稳定的必要条件(Nolan et al.,2001;Zhong et al.,2010).因此,对应飓风强度变化(图1a,b)可以看出,低层PV径向分布的中空结构的建立和维持过程对应于飓风的爆发性增强阶段.到积分32小时后,位涡的最大值点再次出现内移,且随着大值区径向宽度和眼心区位涡量值的增大,位涡的径向梯度开始出现减小的趋势,此后飓风系统增强的速度也明显放缓(图1a,b),飓风强度在积分36小时时达到最强.从雷达回波的分布可以看出,在积分21小时时,距眼心30km左右处出现次眼墙结构,并且次眼墙以明显快于内眼墙的收缩速率向眼心移动;在积分27小时左右,两个眼墙在半径15km处合并,Chen等(2011)将这个过程定义为眼墙合并过程(Eyewall Merging Process:EMP).次眼墙的形成也会引起区域凝结潜热释放,从而影响位涡的量值,这种影响对于切向平均位涡廓线的径向分布可以忽略,但EMP过程中眼墙的快速收缩加速了低层PV的径向输送,有利于中空PV结构的建立.
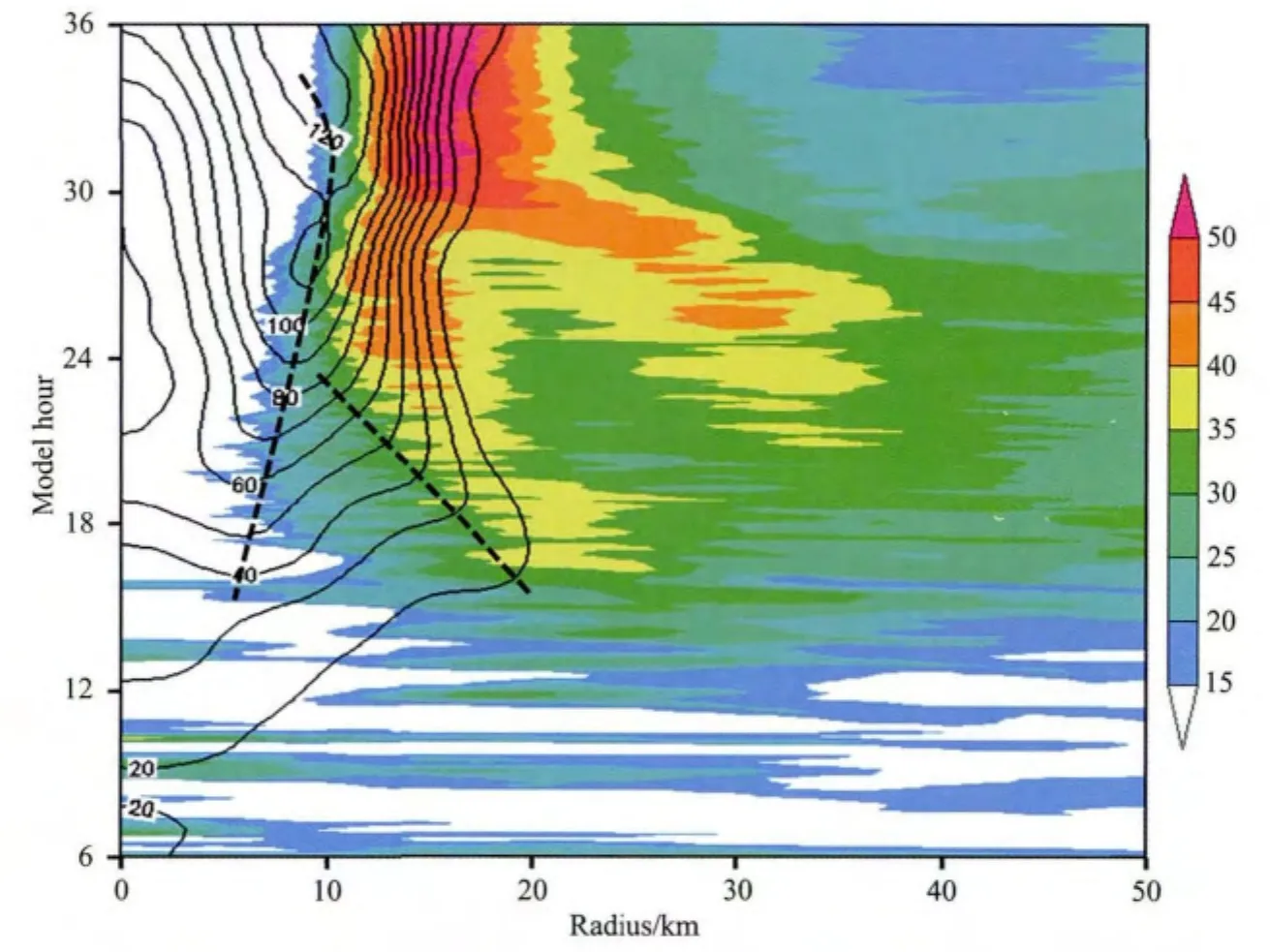
图2 3km高度上切向平均雷达反射率(阴影,单位dBZ)和切向基流位涡(实线,单位PVU)随时间演变,虚线表征径向位涡极值区和次极值区的径向移动趋势Fig.2 Axisymmetric PV (solid,interval=10PVU)as a function of time and radial distance,superimposed with the radar reflectivity(shaded,dBZ),at 3km height from the 36-h model integration between 0000UTC 18and 1200UTC 19Octorber.Dashed lines denote the location of radial top and second maximum PV
由此可见,内核区域位涡的强度和结构变化主要取决于高层暖心下传、中层的凝结潜热释放和低层的动力稳定性,尤其是低层切向平均位涡的结构及其稳定性的变化,这对飓风系统快速增强过程的不同发展阶段具有很好的指示意义.
最后,美国政府在执行制裁政策时会采取个案审查原则,综合考虑个案特殊情况,再做出是否予以制裁的决定。例如,海外资产控制办公室规定了专门的特殊许可制度,对那些本应受到制裁的行为,如果通过海外资产控制办公室的个案审查并得到许可,就可以免受制裁。
3 位涡塔结构和演变特征
从动力学意义上来说,PV是一个能够同时描述旋转和对流作用的物理量,它不仅是热带气旋内部波动形成和传播性质的主要影响因子(Macdonald,1968),其结构和变化还与涡旋系统的稳定性密切相关(Nolan and Montgomery,2001).因此,研究热带气旋内部PV的结构特征,对揭示热带气旋内部深厚对流系统演变以及整个涡旋系统的强度变化都具有指示意义.
为了反映PV在垂直方向的典型结构特征,图3给出了不同积分时刻轴对称PV的经向垂直剖面.在Pre-RI阶段(图3a),高低层的径向流和垂直运动均较弱,垂直方向上存在两个大值PV核,一个位于对流层中下层的眼心区,形成从近地面延伸至6km的单极PVT;另一个位于15km高度以上,其大值中心也位于眼心区,且在高层出流区重力波影响下向外输送.从整层的PV结构来看,对流层高层和低层的高值PV区均由眼心向外单调递减,具有典型的MPVT特征.同时也注意到在对流层中层,由于PV大值区出现径向倾斜的垂直伸展,因而在7km高度上,于半径10~20km处,出现PV量值大于眼心的现象,即在7km高度上,开始有中空结构,其形成原因一方面是由于半径10km附近存在的倾斜上升运动将低层大值PV向上输送,另一方面是对流层中层最强上升运动区凝结潜热释放的影响.
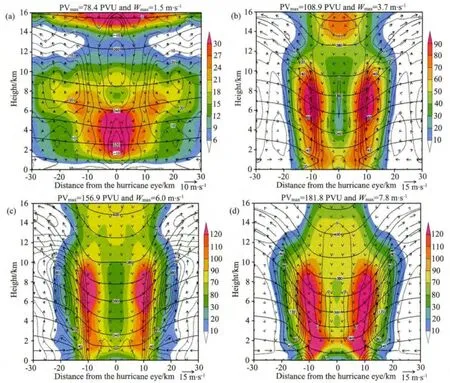
图3 模式资料积分(a)15小时、(b)21小时、(c)29小时和(d)36小时过台风眼心垂直剖面上的轴对称基流位涡(阴影,单位PVU)、非绝热加热率(虚线,单位K·h-1)、位温(实线,单位K)和风矢(单位m·s-1)的分布(图中垂直速度量值均乘以10)Fig.3 Vertical cross section of axisymmetric PV(shaded,PVU),potential temperature(solid,interval=20K),diabatic heating rate(dashed,interval=20K·h-1),and wind vectors(m·s-1)at(a)15hours,(b)21hours,(c)29hours and(d)36hours corresponding to model integration time.The values of vertical velocity all multiplied by 10
进入RI阶段后(图3b),对流层高层的位涡大值区基本维持单极形态,其量值随着眼心处高层大值位温的下传增强到80PVU以上.中层虽然在眼心处同样存在高值位温线向下凹陷,但眼心的位涡增大并不明显,量值均未超过50PVU.而在强上升运动区内侧,中心位于7km高度上,出现了超过60K/h的非绝热大值区,造成对流层中层的非绝热加热等值线密集,对应出现了超过90PVU的PV大值中心,说明随着飓风对流组织化和眼墙结构的建立,凝结潜热释放引起的非绝热加热使得眼墙区对流层中层急剧增温,在眼壁内侧形成强的非绝热加热梯度,进而造成了该区域对流层中层PV的急剧增大,形成了眼心小、外围大的中空环状位涡柱状结构,即中空PVT(HPVT).由于非绝热加热梯度的作用,低层上升运动内侧也开始出现位涡大值区,眼心处的大值区开始出现断裂,说明低层HPVT结构也在建立,飓风系统的不稳定性逐渐增强.
图3c表明积分到29小时,虽然高层暖心持续加强,但眼心处位涡强度基本维持不变.而随着轴对称上升运动最大值增大至6m·s-1,并稳定在半径15km附近,该区域出现了与对流凝结潜热释放相对应的非绝热加热中心,且垂直影响范围从对流层低层3km高度一直伸展到12km,在半径10km附近形成了近乎竖直的高值PV柱状结构.此时的HPVT的物理量配置较前一阶段相比具有以下几个特点:①高值PV柱区域以下沉运动为主,使得中层高值位涡向低层输送,有利于低层最大风速半径内侧PV量值增大和低层HPVT建立;②低层HPVT建立后,径向扰动风速增强,使得低层径向流增强,并在高值PV区两侧形成辐合,加强了水平PV向最大风速半径内侧的输送,它同时又有利于HPVT结构的维持和发展;③整体高值PV柱径向宽度变窄,眼心到PV大值区的梯度增大,说明整个基态涡旋系统的不稳定性呈现加强的趋势,有利于飓风系统的爆发性增强.
发展到最强时刻(图3d),随着眼墙区对流的持续加强,非绝热加热率增大至超过120K/h,非绝热加热率等值线密集的区域发生在半径15km附近,位于最强上升运动的内侧,使得该区域的位涡增加.并且在强对流的垂直混合作用下,凝结潜热加热区以及相对应的HPVT的高值柱状区内垂直分布趋于均匀.同时由于高值位涡柱两侧径向风速增大,使得高值PV向眼心输送,高值PV区的径向宽度较爆发增长阶段(图3c)增大,尤其在3km高度上形成了一个贯穿眼心的高值位涡桥状结构,表明低层眼心两侧的高值位涡区由于基态涡旋动力不稳定造成径向混合最为明显,这与Hendricks和Schubert(2010)理想实验分析结果一致.随着PV径向混合增强,眼心区整体PV量值增强到60PVU以上,说明高值PV已经存在向中心填塞的趋势,预示眼心两侧的高值位涡区将趋于崩溃,HPVT开始向MPVT转化,基态涡旋系统也随之趋于稳定.
从切向平均PV的垂直分布可以看出,HPVT结构最早出现在对流层中层,但与动力稳定性扰动增长联系最紧密的HPVT结构则出现在低层3km左右高度上,且该高度上HPVT结构的建立和崩溃对飓风强度的突然变化以及变化速率具有很好的一致性,因此分析3km高度上飓风增强不同阶段的位涡和水平风场的分布情况(图4),从图中可以看出,Wilma(2005)在Pre-RI阶段,内核区域整体PV量值较小,基本呈现单极分布特征,PV最大量值为40.5PVU,且高PV核均集中在眼心区域(图4a).进入RI阶段后,虽然水平切向风速增大,系统旋转增强,但眼心处PV维持在50PVU以下,而在最大风速半径内侧(半径10km附近)出现了高值PV的环状结构,其中镶嵌有90PVU左右的大值PV核,说明此时位涡内核区域的径向分布开始出现眼心量值较低的典型“中空”结构.到积分29小时(图4c),水平风速继续快速增大,PV的高值环状结构内缩至半径10km以内,环的宽度变窄且形状更为对称;同时最大风速半径内侧大值PV核的最大值达到128PVU,而眼心处的PV值仍然维持在50 PVU以下,说明PV环的中空结构更加明显,此时飓风系统也对应出现爆发性增强.到飓风强度最强时刻,高值位涡环的量值和位置基本维持,但此时眼心的PV量值增大至90PVU,环的宽度自眼墙内侧向内不断加厚,眼心区域出现高值PV填塞,中空环状结构逐渐消失,说明位涡的径向结构向单极分布转化,随后飓风系统进入强度衰减期.

图4 模式资料积分(a)15小时、(b)21小时、(c)29小时和(d)36小时3km高度上的位涡(阴影,单位PVU)和水平风矢(单位m·s-1)的分布Fig.4 Horizontal PV (shaded,PVU)and wind vector(m·s-1)at 3km height at(a)15hours,(b)21hours,(c)29hours and(d)36hours corresponding to model integration time
通过分析热带气旋增强过程中不同阶段PV的水平和垂直分布可知,位涡塔在热带气旋发展的不同阶段表现为不同的结构特点.动力学分析表明,位涡塔的结构与基流涡旋系统的稳定性密切相关,而热带气旋基本涡旋系统的几类稳定性,包括正压不稳定、代数不稳定、混合不稳定等,都具有一个相同的必要条件,即基流位涡(正压无辐散条件下退化为涡度)在径向分布上存在除眼心外的另一个最大值点.这个条件反映到实际热带气旋个例的三维分布上,就体现为典型的HPVT结构.因此,HPVT结构的建立和崩溃对应于涡旋系统动力稳定性的转折,对热带气旋强度的突然变化产生重要影响.
4 位涡塔对热带气旋强度变化的影响
在高层增温、潜热释放和对流垂直混合作用下,PVT的结构出现MPVT和HPVT的相互转化,也造成了涡旋系统动力稳定性的变化.但是这种结构分布只能定性描述系统是否具备动力不稳定的条件,如何描述PVT特征以及不同PVT结构对稳定性的影响还需要进一步定量化研究.
Schubert等(1999)提到在正压模式中的线性稳定性问题时认为,不稳定增长率是一个与内核区域平均涡度、切向波数、PV环的厚度以及中空度取值有关的函数.因此,基于分析稳定性的环状涡度的定 义 (Michalke and Timme,1967),Schubert 等(1999)定义了高值涡度环的相对厚度(Thickness)δ和中空度(Hollowness)γ.其中δ表征眼墙内侧涡度发生陡增的半径长度与眼墙外侧环境涡度骤减的半径长度之比,γ表征眼心的相对涡度ζ1与内核区的平均相对涡度ζav之比.根据Schubert等(1999)构造的基态涡度函数
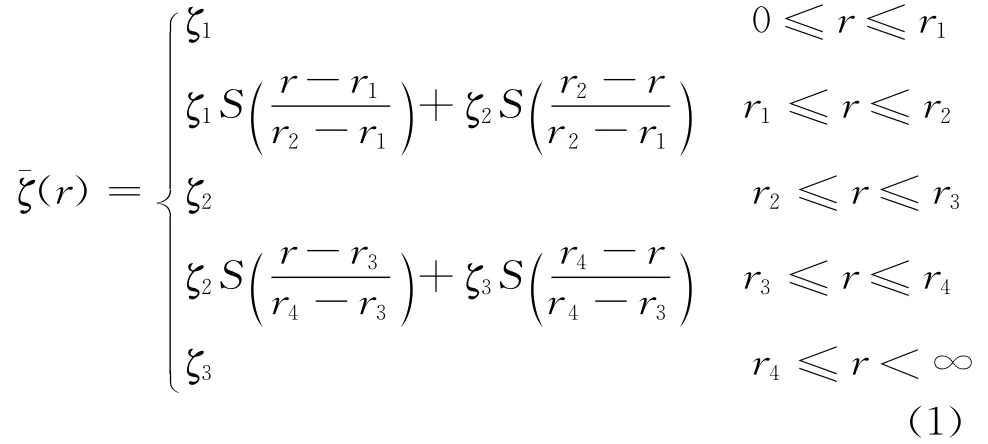
其中ζ1、ζ2、ζ3、r1、r2、r3和r4为常数,S(x)=1-3x2+2x3为Hermite形状函数,可以控制涡度的径向分布结构,r2与r3之间距离为眼墙区域,r1与r2之间和r3与r4之间的区域分别为涡度发生跃变(陡增和骤减)的过渡区.
Hendrick等(2009)重新定义了高值涡度环的相对厚度,而中空度的定义与Schubert等(1999)一致,即γ=ζ1/ζav,且ζav取为经验常数2.0×10-3s-1.对于相对厚度,则在眼墙内侧涡度陡增的半径r1和眼墙外侧环境涡度骤减的半径r4的基础上,综合考虑涡度径向极值的内、外边界半径r2和r3,重新定义的相对厚度的表达式为δ= (r1+r2)/(r3+r4).同时Hendrick等(2009)进行了大量理想实验,证实了当热带气旋内存在薄且空(δ大,γ小)的涡度环状结构时,扰动增长率大,热带气旋快速加强;当热带气旋内涡度环的结构厚且实(δ小,γ大)时,扰动增长率小,热带气旋强度变化减缓.对于非常厚的环来说,系统近似为稳定的.由于正压无辐散条件下PV可退化为涡度,因此涡度径向结构的理想实验,可帮助理解不同基态涡旋廓线对飓风系统稳定性的的影响.
为了定量地描述Wilma不同阶段位涡环的结构,讨论HPVT建立和崩溃对热带气旋强度变化的影响,本节将相对厚度和中空度这两个结构参数引入实际个例的位涡诊断分析中.图5a给出了Hendrick等(2009)根据基态涡度函数(方程(1))得到的经典理想廓线及其基态涡度函数中各半径参数的定义,可以看出r1和r4分别对应了涡度梯度陡增和骤减的位置,r2和r3则近似表征位涡大值区的边界.而与由模拟结果轴对称后得到的PV廓线(图5b)比较可以发现,实际个例中,眼心到PV最大值点的变化没有明显的突变点,同时PV大值区量值变化大,峰值区域也较窄,因此在对实际个例中HPVT参数的选择和计算时,一方面参照Hendrick等(2009)理想试验的结果,另一方面在计算实际飓风HPVT的相对厚度和中空度时,对相关参数的选择方法进行了修正,采用位涡增长率极值的概念定义位涡发生跃变的位置,即用位涡梯度廓线的波峰和波谷的位置来定义表达式中r1和r4的取值;其次,将平均基流位涡值达到峰值的90%以上(包括90%)的区域作为峰值区域,并将这个区域的内外边界分别取为表达式中r2和r3的取值;最后由于对飓风内核区域没有明确定义,因此本文直接用眼心处的位涡值(q1)与径向位涡的峰值(qm)之比来计算位涡环的中空度.根据修正后的参数定义,确定了模拟过程中飓风 Wilma在RI阶段位涡环对应的r1、r2、r3和r4的位置,并计算得到飓风RI阶段每30min相对厚度和中空度的值.
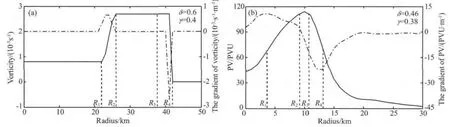
Fig.5 (a)理想实验(Hendrick,2008)基态绝对涡度(实线,单位s-1)和径向绝对涡度梯度(点虚线,单位s-1·m-1)的分布与(b)模式资料积分24小时典型轴对称位涡(实线,单位PVU)和径向位涡梯度(点虚线,单位PVU·m-1)的分布比较.图5a中用虚线标注了理想实验定义的半径参数,其中的R1和R4对应于眼墙内侧涡度陡增半径和眼墙外侧环境涡度骤减的半径,R2和R3表征涡度径向极值的内、外边界半径.图5b中虚线则表示了用于模式资料位涡结构计算的半径参数,其中R1和R4对应于位涡梯度波峰和波谷的位置,R2和R3对应于平均基流位涡值达到峰值的90%以上(包括90%)的内外边界半径Fig.5 (a)Radial distribution of basic absolute vorticity (solid,10-3 s-1)and absolute vorticity gradient(dotteddashed,s-1·m-1)used in theoretical simulation by Hendrick(2008).Dashed lines indicate the radius parameters.R1 and R4denote the radius of vorticity increasing rapidly and decreasing sharply,respectively.R2and R3denote the inner and outer boundary radius of vorticity peak.(b)Radial distribution of axisymmetric PV(solid,PVU)and axisymmetric PV gradient(dotted-dashed,PVU·m-1)at 24hours corresponding to model integration time.R1and R4correspond to locations of crest and trough for PV gradient,respectively.In addition,R2and R3denote the boundary radius to the region whose values are more than 90% (including 90%)of the peak
根据相对厚度和中空度的参数定义可知,当PV基态廓线表现为 MPVT特征时,r1=0,q1=qm,则相对厚度和中空度分别为0和1,说明飓风系统是稳定的.随着HPVT的建立,相对厚度越大,中空度越小,则说明水平高值PV环薄且空;相对厚度小,中空度大,则说明PV环厚且实.
将飓风快速发展阶段(积分15~36小时)每间隔30min的位涡环结构参数量值与飓风未来每30min的强度变化进行相关分析(表1)可以看出,位涡环的相对厚度、中空度与未来每30min的最低海平面气压变化(DPmin)的相关系数分别为0.58、-0.53,与未来每30min最大风速变化(DUmax)的相关系数分别为-0.2、0.15.其中 HPVT结构参数与未来每30min的最低海平面气压变化率的相关系数通过了99%的置信度检验,说明HPVT的结构参数与飓风系统强度变化具有良好的相关性,而最大风速变化则未通过.

表1 低层位涡环结构参数与飓风强度变化的相关系数Table 1 The correlation coefficients between structural parameters of low-level PV rings and intensity change of hurricane
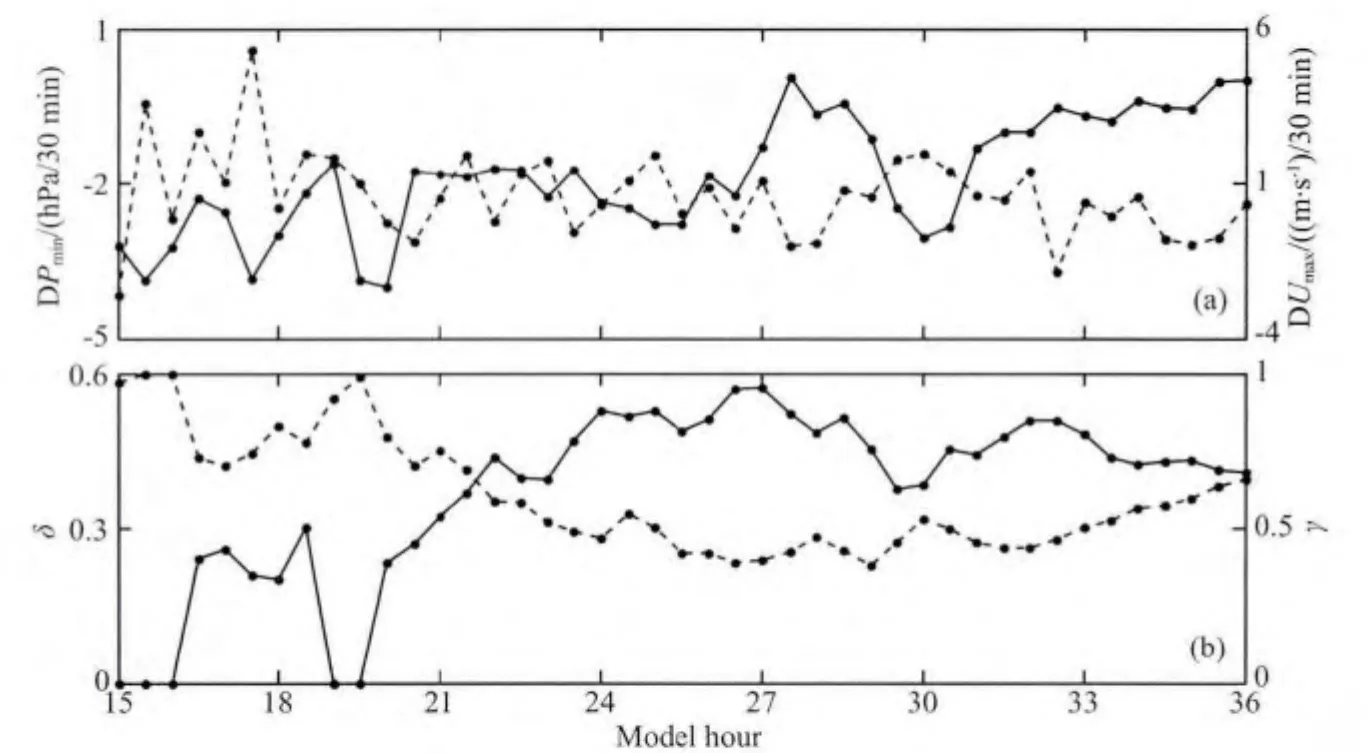
图6 快速增强阶段(a)飓风强度和(b)低层径向位涡结构参数随时间演变.(a)中实线表征最低海平面气压每30min的变化(DPmin,单位hPa/30min),虚线表征最大地面风速每30min的变化(DUmax,单位(m·s-1)/30min);(b)中实线表征相对厚度,虚线表征中空度Fig.6 Time series of the variations of(a)Pmin(solid,hPa/30min)and Umaxin 30minutes(dashed,(m·s-1)/30min);and(b)two structural parameters,in which thickness and hollowness are denoted by solid and dashed line,respectively
进一步分析飓风强度变化与位涡环的两个形态参数在RI阶段的演变趋势(图6)可以看出,刚进入RI阶段,高值位涡区接近眼心,位涡环的相对厚度为0,中空度为0.97,说明高值位涡区的位置逐渐向外移动,位涡峰值开始移出眼心区域,形成高值位涡环状结构,系统开始出现不稳定.在随后的12h内,相对厚度δ的值单调增大,中空度γ的值基本单调减小,到积分27时相对厚度的量值达到0.57,中空度的值则降低至0.40,从这两个参数的时间演变来看基本达到各自的最值,说明此时PVT的结构薄且空,高值位涡环内外梯度达到最大,同时高值位涡环径向宽度也最小,系统的不稳定性最大.对应于飓风海平面最低气压与地面最大风速两者未来每30min变化(图6a)的时间演变可以看出,在积分15~27小时内,飓风系统也处于爆发性增强的阶段,最明显体现在最低海平面气压的变化,其每30min降低2hPa以上.在这段时期内,需要注意的是地面最大风速在前6小时表现为较为一致的增强趋势,但是到积分21~27小时内,最大风速的每30min变化却出现了正负量值交替出现的现象,说明当高值位涡环在变薄变空的过程中,飓风系统的稳定性与地面最大风速的变化并不一致.Chen等(2011)在对Wilma(2005)的生命史回顾中也发现,在其RI过程中,后6小时的气压与风速的变化与前6小时的气压与风速满足的经典梯度平衡关系表现不一致.Hendrick(2008)与 Hendrick和Schubert(2010)利用正压涡度守恒方程的理想模型讨论PVT分布特征对基态涡旋结构和强度变化的影响时指出,当HPVT向MPVT转化时,在PV输送和混合作用下,基态涡旋中心气压和最大风速均发生减小.这也就说明随着高值位涡环变薄变空,中心气压随之减小,并在梯度风平衡约束下使得最大风速出现增长,有利于飓风系统的强度增强;但是在PV输送和混合作用下产生的最大风速减小,又会阻碍飓风发展.因此表现在实际模拟个例中,就会出现当HPVT不稳定结构发展到一定阶段后,气压减小量趋于稳定而最大风速变化量在正负值之间出现跳跃变化,系统增强的整体速度较RI过程初期有所减小(图6a).
积分27h后,HPVT的相对厚度(中空度)参数表现为振荡性减小(增大)的趋势.期间从积分27~31小时,相对厚度和中空度的振荡变化比较明显,相对厚度和中空度基本维持在0.45和0.4上下浮动(图6b).相对应地,飓风的最低海平面气压和最大地面风速的每30min变化的量值均较前一阶段出现较大波动,飓风增强的速度进一步减弱.到积分31小时后,相对厚度和中空度分别进入单调减小和增大阶段(图6b),说明径向高值位涡环的径向宽度增大,环内位涡极值所在半径开始向内移动,高值位涡开始向眼心输送,眼心的位涡低谷迅速被填塞,系统不稳定性减弱.由此说明,尽管在RI发展后期PV分布存在环状结构,但随着眼心区域被高值位涡填塞,出现厚而实的环状结构,使得系统趋于稳定,此时可以将热带气旋的扰动看做稳定增长(Knaff et al.,2003).随后飓风的最低海平面气压和最大风速的每30min变化率均向0值逼近(图6a),到积分36小时,最低海平面气压和最大风速在30min内变化分别为0.02hPa和0.34m·s-1,飓风开始进入维持减弱阶段.
5 结论和讨论
基于位涡径向非均匀分布对飓风系统稳定性影响的理论研究,本文利用实际飓风个例的高分辨率模拟资料,研究PVT的强度和结构及其演变在飓风快速增强过程中所起的作用,得到飓风内中尺度结构分析的几点结论.
(1)在对流层中低层,飓风内位涡异常的大值中心随时间的演变过程与飓风强度变化具有同位相的变化特征.中层位涡异常大值中心取决于系统发展初期形成的高层位涡异常大值中心的下传和对流发展引起的中层凝结潜热释放,中层位涡的强度变化与飓风发展同步;而低层位涡异常大值中心的强度变化满足动力稳定性条件,因而位涡异常分布和演变对飓风快速增强不同阶段具有指示性.
(2)分析飓风内PVT的垂直和水平结构及其演变,揭示了飓风不同发展阶段MPVT和HPVT两种不同结构间的相互转化以及它们与涡旋系统动力稳定性相联系的物理图像.在Pre-RI阶段,PV的整体结构具有典型的MPVT特征;进入RI阶段,在高层增温、潜热释放和对流垂直混合作用下,HPVT的结构开始建立,系统的不稳定性加强,飓风出现爆发性增强;随后,PV径向混合增强,HPVT崩溃,基态涡旋系统也随之趋于稳定.
(3)根据飓风不同发展阶段的PVT的结构特征,用修正后的位涡环的两个结构参数(相对厚度和中空度),定量描述HPVT的结构特征以及相应的稳定性,并分别与飓风的强度变化进行相关分析,结果表明HPVT的结构参数与飓风强度变化的相关性通过了显著性检验,能够作为飓风强度变化的高相关因子.同时也验证了HPVT的不稳定性对飓风海平面气压和最大风速均具有减小作用的理论分析结果.
在个例分析的基础上,利用历史的飓风过程进行合成分析,讨论上述结果的普遍意义是我们今后进一步研究的工作.
致谢 感谢美国马里兰大学的张大林教授提供的飓风Wilma(2005)高分辨率模式输出资料,并感谢他对本文提出了许多宝贵的意见.
Aberson S D,Black M,Montgomery M T,et al.2006.Hurricane Isabel(2003):New insights into the physics of intense storms.Part II:Extreme localized wind.Bull.Amer.Meteor.Soc.,87(10):1349-1354.
Bender M A,Ginis I,Kurihara Y.1993.Numerical simulations of tropical cyclone-ocean interaction with a high-resolution coupled model.J.Geophys.Res.,98(D12):23245-23263.
Bender M A.1997.The effect of relative flow in the asymmetric structure in the interior of hurricanes.J.Atmos.Sci.,54:703-724.Chen H,Zhang D L,Carton J,et al.2011.On the rapid intensification of Hurricane Wilma (2005).Part I:Model prediction and structural changes.Wea.Forecasting,26(6):885-901
Chen H,Zhang D L.2013.On the rapid intensification of Hurricane Wilma(2005).Part II:Convective bursts and the upper-level warm core.J.Atmos.Sci.,70:146-162.
Chen L S,Ding Y H.1979.Generality of Western North Pacific Typhoons(in Chinese).Beijing:Chinese Science Press,403.
Duan Y H,Qin Z H,Gu D F,et al.1998.Numerical study on the effects of sea surface temperature on tropical cyclone intensity-Part I:Numerical experiment of the tropical cyclone intensity related to SST.Acta Meteorologica Sinica,12(2):142-148.
Hendricks E A.2008.Tropical cyclone evolution via internal asymmetric dynamics[Ph.D.Dissertation].Colorado:Colorado State University.
Hendricks E A,Schubert W H,Taft R K,et al.2009.Life cycles of hurricane-like vorticity rings.J.Atmos.Sci.,66(3):705-722.
Hendricks E A,Schubert W H.2010.Adiabatic rearrangement of hollow PV towers.J.Adv.Model.Earth.Syst.,2:1-19.
Holland G J,Wang Y Q.1999.What limits tropical cyclone intensity.∥Preprint of the 23rd Conference on Hurricanes and Tropical Meteorology.Amer.Meteor.Soc.,Dallas,Texas,955-958.
Houze Jr R A,Chen S S,Smull B F,et al.2007.Hurricane Intensity and Eyewall Replacement.Science,315(5816):1235-1239.
Knaff J A,Kossin J P,De Maria M.2003.Annular hurricanes.Wea.Forecasting,18:204-223.
Macdonald N J.1968.The evidence for the existence of Rossby-like waves in the hurricane vortex.Tellus,20(1):138-150.
Michalke A,Timme A.1967.On the inviscid instability of certain two-dimensional vortex-type flows.J.Fluid Mech.,29(4):647-666.
Möller J D,Smith R K.1994.The development of potential vorticity in a hurricane-like vortex.Quart.J.Roy.Meteor.Soc.,120(519):1255-1265.
Montgomery M T,Kallenbach R J.1997.A theory for vortex rossby-waves and its application to spiral bands and intensity changes in hurricanes.Quart.J.Roy.Meteor.Soc.,123(538):435-465.
Montgomery M T,Vladimirov V A,Denissenko P V.2002.An experimental study on hurricane mesovortices.J.Fluid Mech.,471:1-32.
Montgomery M T,Bell M M,Aberson S D,et al.2006.Hurricane Isabel(2003):New insights into the physics of intense storms.Part I:Mean vortex structure and maximum intensity estimates.Bull.Amer.Meteor.Soc.,87(10):1335-1347.
Nolan D S,Montgomery M T,Grasso L D.2001.The wavenumber-one instability and trochoidal motion of hurricane-like vortices.J.Atmos.Sci.,58(21):3243-3270.
Schubert W H,Alworth B T.1987.Evolution of potential vorticity in tropical cyclones.Quart.J.Roy.Meteor.Soc.,113(475):147-162.
Schubert W H,Montgomery M T,Taft R K,et al.1999.Polygonal eyewalls,asymmetric eye contraction,and potential vorticity mixing in hurricanes.J.Atmos.Sci.,56(9):1197-1223.
Terwey W D,Montgomery M T.2008.Secondary eyewall formation in two idealized,full-physics modeled hurricanes.J.Geophys.Res.,113:D12112.
Wang Y,Wu C-C.2004.Current understanding of tropical cyclone structure and intensity changes—a review.Meteor.Atmos.Phys.,87(4):257-278.
Zhong W,Zhang D L,Lu H C.2009.A theory for mixed vortex Rossby-gravity waves in tropical cyclones.J.Atmos.Sci.,66(11):3366-3381.Zhong W,Lu H C,Zhang D L.2010.Mesoscale barotropic instability of vortex Rossby wave in tropical cyclones.Adv.Atmos.Sci.,27(2):243-252.
附中文参考文献
陈联寿.丁一汇.1979.西太平洋台风概论.北京:科学出版社,403.
陈联寿,徐祥德,罗哲贤.2002.TC动力学引论.北京:气象出版社.

