波形钢腹板－钢管混凝土组合结构人行天桥的动力性能研究

曾显通

(嘉博(福建)联合设计有限公司 福建福州 350001)

引 言

未来城市人行桥的发展必定会向着大跨、轻巧、美观、施工方便快捷并不阻挠桥下交通的方向发展，钢结构体系无疑具有强大的竞争优势，但轻、薄、柔的钢结构体系又会引发新的振动问题，特别是当人行天桥的自振基频降低到同行人荷载激励的频率相当时，容易引发人行桥振动幅度过大，造成人群恐慌，甚至发生踩踏事故等问题，故深入开展人行桥的结构动力优化设计，找到经济效益好而动力性能又优越的钢结构体系无疑是一重大研究课题。

波形钢腹板－钢管混凝土组合结构(图1)作为一种新型组合结构，由福州大学的陈宝春[1][2]等人提出，并对这种组合结构的力学性能进行了一系列的实验和理论研究，研究得出这种组合结构能发挥钢管混凝土抗弯承载力高和波形钢腹板抗剪切屈曲能力强的优点。其作为腹板的波形钢，与混凝土腹板相比，具有自重小，施工方便等优点;与平钢腹板相比，具有抗剪、抗扭性能高等优点;加之，它有轻巧美观的外形、施工也较方便快捷，可以说它在城市人人行天桥中具有广泛的应用前景。不过，反映一个结构整体性能的高低，不仅仅要看它的静力性能，也要看它的动力性能，目前人们对这种新型组合结构的研究甚少，本文将运用大型通用有限元软件根据实桥建立有限元模型，通过对比分析这种新型组合结构人行天桥和平钢腹板组合人行天桥在行人荷载作用下的动力响应以判断这种新型组合结构体系的动力性能，以期为工程实际提供参考。

图1 波形钢腹板－钢管混凝土组合结构

1 工程概况

侨英人行天桥位于厦门市集美区同集路上，为改善该路段的交通起到了重要作用。该桥为双跨等截面波形钢腹板钢管混凝土组合连续梁桥，跨径布置为28.0m+31.0m，主梁梁高1.4m，上、下弦管均采用300×400×14mm的型钢钢管，管内填充C30微膨胀混凝土。腹板、顶板及悬臂均采用Q345C波形钢板如(图2)，波高160mm，钢板结构层上浇C30混凝土作为桥面板。桥面净宽4m，含栏杆全宽4.3m，设两道腹板、中心距为2.3m，悬臂为1m。天桥实景如下(图2)所示。

2 有限元模型的建立

运用大型通用有限元软件ANSYS建立了该桥的全桥空间整体有限元模型，其中，钢管和波形钢腹板采用壳单元模拟，共45351个单元，42910个结点，每个结点具有6个自由度，分别为 Ux、Uy、Uz、ROTx、ROTy、ROTz;桥面混凝土和管内混凝土采用实体单元模拟，共102104个单元，66951个结点，每个结点具有3个自由度，分别为Ux、Uy、Uz;横撑采用梁单元模拟，共791个单元，799个结点，每个结点具有6个自由度，分别为Ux、Uy、Uz、ROTx、ROTy、ROTz。将波形钢腹板用平钢腹板代替建立了腹板为平钢腹板的人行桥有限元模型，两座人行天桥的有限元模型图如(图3、4)。

图2 天桥实景图

图3 平钢腹板人行桥有限元模型图

图4 波形钢腹板人行桥有限元模型

3 两座人行天桥的固有振动特性分析

结构本身固有的动力特性决定了结构的振动特点，是研究所有振动问题的前提[3]，通过模态分析可以得到结构的自振频率和各阶振型。人行天桥的前8阶振型见(表1)，各阶振动频率见(表2)。

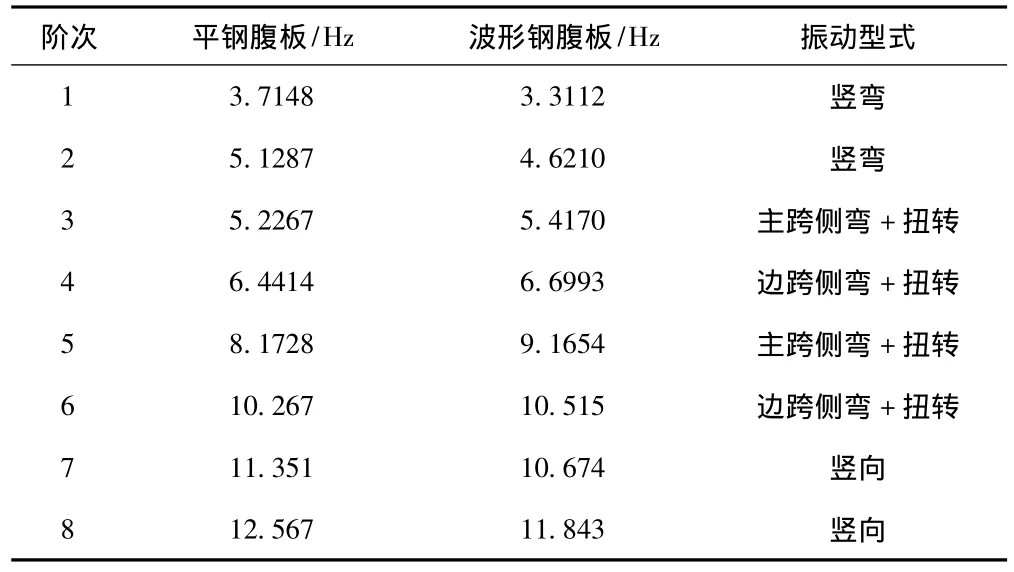
表1 两种组合人行天桥的前8阶自振频率

从表中可以看出，当振动形式为竖向弯曲时，平钢腹板组合人行桥的自振频率都要大于波形钢腹板组合人行桥的自振频率;而当振动形式为侧向弯曲并伴随扭转时，平钢腹板组合人行桥的自振频率都要小于波形钢腹板组合人行桥。前者主要是因为波形钢腹板的褶皱效应使得波形钢腹板的弯曲及轴向刚度远小于平钢腹板的缘故，后者是因为波形钢腹板的侧向及扭转刚度要大于平钢腹板的缘故。

4 人行荷载模型

人行荷载激励具有显著的周期性，其竖向分力和侧向分力都可以用傅里叶级数表示，但竖向分力和侧向分力的基频有所不同。竖向激励是由人行走时重心的上下起伏对桥面产生的竖直方向上的动力荷载引起，一个单步即是一个循环，正常行走时约为2HZ，跑步时为4HZ。侧向激励则是由人的重心从一只脚移到另外一只脚时，身体呈侧向Z字形移动产生的周期性激励引起，且左右脚各跨出一步后才算完成一个循环(即2个单步)。所以，人行荷载激励的侧向基频总是竖向基频的一半[4]。

图5 行人行走荷载示意图

4.1 单人荷载

目前，国内外普遍采用的人行单步荷载激励为一傅里叶级数表示的简谐波，分竖向荷载和侧向荷载，其中竖向荷载表达式为[5]:

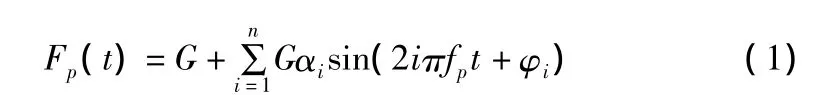
而行人激励产生的侧向荷载仅是波动的周期分量，可用下式表示[5]:

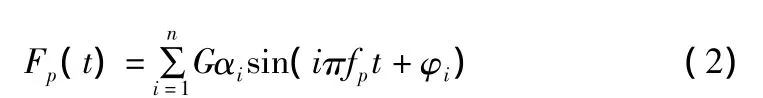
式中:G—行人体重;fp—竖向步频;i—谐波阶数。

αi——第阶荷载谐波的竖向动载因子。

φi——竖向谐波相位角。

大量研究表明，人行桥的人致振动响应主要由步行力一阶谐波产生，为简化荷载模型，分析中仅考虑步行力的一阶谐波，表达式为:

单人竖向:

单人侧向:

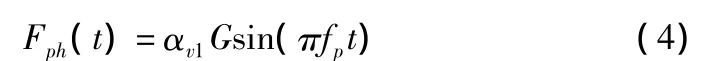
式中:取动载因子αv1=0.5，人的体重G=700N，并假定初始相位为零。鉴于平钢腹板人行桥和波形钢腹人行桥的基频都大于3HZ，这里的步频取为人的跑步频率fn=4Hz。其中，竖向单步荷载取式(3)中正弦波的半波荷载。

4.2 人群荷载

当人群荷载作用在桥面上时，由于各人的体重、位置、步频等存在差异，导致人群荷载的不确定性即随机性。为研究人群荷载作用下人行桥的响应，有学者提出一种较简单的方法是在单个行人荷载的基础上乘以一个影响系数[6]，即:

Matsumoto等[7]研究随机步行人群对人行桥的激振时，假设行人上桥事件服从泊松分布，且相位互不相关，根据随机振动理论得出:

分析中采用以上简化模型，假设桥上人流密度为0.6人/m2，则人数 N=0.6×4.3×31≈80，等效为9 个步调一致的人同时通过桥面，则人群倍增因子m=9，表达式为:

人群竖向:

人群侧向:

式中的Fpv(t)、Fph(t)分别为单人竖向与侧向步行激励。

5 加载工况及其有限元模拟

以腹板为平钢腹板的有限元模型称为A，腹板为波形钢腹板的有限元模型称为B。与B相比，A除腹板用等钢量的平钢板代替外，其余条件同B模型一致。为对比两种腹板人行桥的人致振动特性，对两个模型施加相同的荷载工况，共4种:

①单人竖向加载

②单人侧向加载

③人群侧向加载

④人群侧向加载

单人荷载激励取4.1节中描述的荷载模型。根据前人的调查[8]，取行人单个步长为0.64m，即在模型上沿桥面纵向每隔0.64m创建节点，共94个。单人跑步荷载(竖向)激励的步频f=4Hz，周期t=1/4=0.25s，(而跑步荷载的侧向激励由于是左右脚各一步才是一个变化周期，故其频率为竖向值的一半，即2Hz)。则人行荷载作用时可视为一连续的周期荷载以0.64f的移动速度作用在桥面上。

单人过桥时，步行荷载沿桥面纵向中心线作用，其竖向步行荷载作用在每个节点上的时间为0.25s，过桥总时间为23.5s。而侧向激励过桥总时间与竖向相同。人群过桥时，为9个步调一致的单步荷载同时作用在等宽等间距的9个节点上，人与人之间间隔一个步伐(即一个节点)，沿将桥面宽度四等分的三条纵向线移动作用，每排节点被作用三次，假设一开始9个人就都已站在桥头，则过桥总时间仍为23.5s。

6两种人行天桥的振动响应时程分析

分别对A和B施加几种不同工况下的人致激励荷载，在相同的工况下比较两桥的时程参量(位移和加速度等)。取不利位置处的最大位移(m)和加速度(m/s2)作为对比的标准。当行人荷载作用在桥面上相当于一移动荷载作用在梁上，不利位置是跨中截面，(作用时间正好是行人作用在人行桥跨中顶面时所产生的动力响应。)这里为主跨(31m)跨中截面。取跨中截面上顶面中点和左右梁底处位移和加速度的响应最大值作为对比，其值在竖向人行荷载和侧向人行荷载作用下的对比如下(表2，3)。从表中可以看出，不管是竖向还是侧向行人荷载作用下，B桥最不利位置处的位移和加速度响应最大值都要较A桥的小。

表2 竖向人行荷载作用下A和B桥主跨跨中截面最大位移与最大加速度值

表3 侧向人行荷载作用下A和B桥主跨跨中截面最大位移与最大加速度值

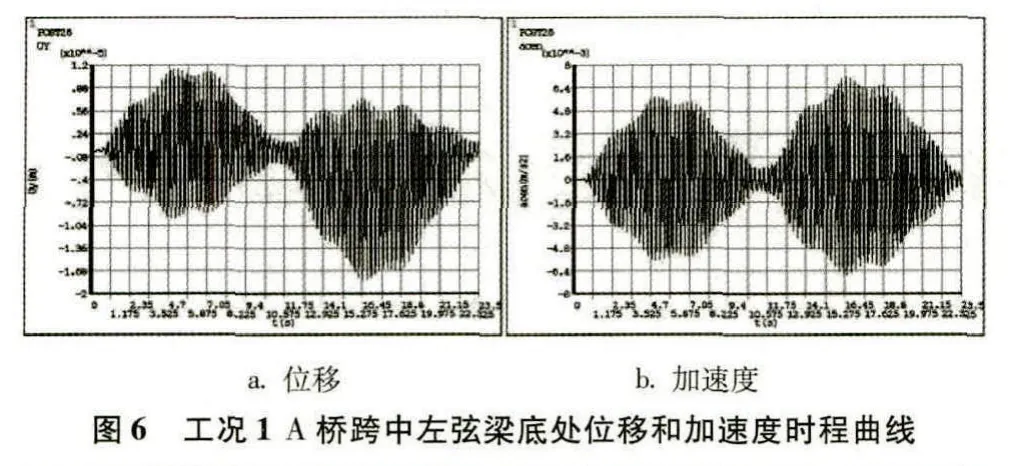
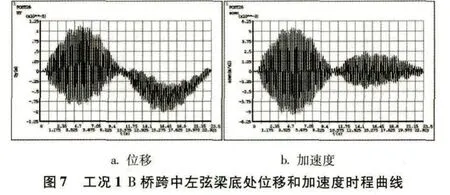
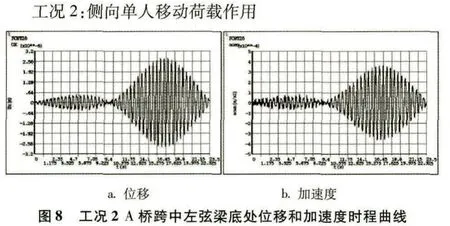
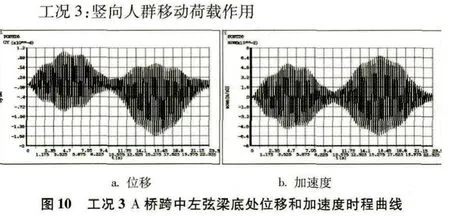
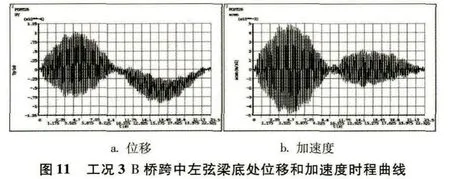
时程曲线是反映位移或加速度随时间变化规律的曲线，可以很直观地对得出的结果(有限元点算求解)进行对比分析。以下为4种工况下跨中截面左弦梁底测点处在移动荷载作用时间内的位移和加速度时程曲线，如(图6)到(图13)所示。对比工况1竖向单人移动荷载作用下A桥与B桥的位移和加速度时程曲线可以发现，当移动荷载作用在主跨时，B桥测点处的位移和速度波动幅值明显要比A桥的要小，而(图7)中位移时程曲线出现很明显的下挠形状，是因为波形钢腹板的折叠效应导致腹板轴向和弯曲刚度几乎为零的缘故。工况3同理。工况2、4中波形钢腹板组合人行桥测点处的位移和速度波动幅值均要比平钢腹板组合人行桥的要小，是由于波形钢侧向刚度大于平钢腹板的缘故。

工况1:竖向单人移动荷载作用

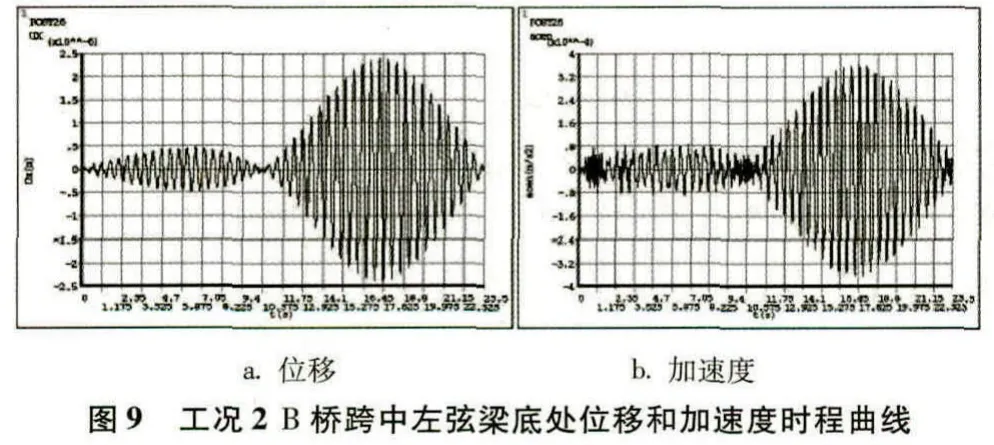
工况4:侧向人群移动荷载作用

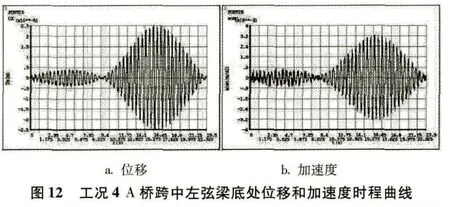
图13 工况4 B桥跨中左弦梁底处位移和加速度时程曲线

7 结论

为研究波形钢腹板－钢管混凝土组合人行桥的动力性能，将其与等钢量的平钢腹板作人致振动对比分析。首先对比分析了两座人行桥的固有振动特性(自振频率和模态)，分析发现，平钢腹板组合人行桥对应竖向弯曲模态的自振频率都要较波形钢腹板组合人行桥的高，而对应侧向弯曲并伴随扭转模态的自振频率都要较波形钢腹板组合人行桥的低。然后分四种工况对比分析了两种腹板人行桥的人致振动情况，人行荷载取简化后的半波正弦跑步荷载模型，将其视为一移动荷载作用于桥面上。分析给出了两种人行桥最不利位置处在四种工况下的位移和加速度响应时程曲线，结果表明，不管是竖向还是侧向行人荷载作用下，波形钢腹板组合人行桥最不利位置处的位移和加速度响应最大值都要较平钢腹板组合人行桥的小，说明波形钢腹板组合人行桥的动力性能要优于平钢腹板。

[1]陈宝春，高婧.波形钢腹板钢管混凝土梁受弯试验研究[J].建筑结构学报，2008，29(1):75 －82.

[2]高婧，陈宝春.波形钢腹板钢管混凝土梁有限元分析及参数研究[J].福州大学学报，2008，36(5):722 －728.

[3]袁旭斌.人行桥人致振动特性研究[D].上海.同济大学，2006.

[4]金志坚.人行桥人致振动分析[D].长沙.湖南大学.2009.

[5]Obata T，Miyamori Y.Identification of a human walking force model based on dynamic monitoring data from pedestrian bridges.Computers and Structures，2006，84(1):541 －548.

[6]欧家富，周云开.人行桥行人荷载的动力特性及作用模型分析[J].广东建材，2010，01:14 －17.

[7]Y.Matsumoto，T.Nishioka，H.Shiojiri，K.Matsuzaki，Dynamic design of footbridges，IABSE Proceedings，No.P －17/78，1978，pp.1–15.

[8]金巨东.波纹腹板钢箱梁人行桥人致振动研究[D].郑州大学，2012.