厦门海沧体育中心体育场风荷载数值模拟计算

匡子佑，肖伟，杨玛莎，徐洪勇

(厦门合道工程设计集团有限公司 福建厦门 361002)

1 提出问题

图1 海沧体育中心整体效果图

海沧体育中心由主体育场、游泳馆、综合馆、门球馆等组成(图1)。主体育场长轴 292m，短轴 200m，钢结构屋盖最高点高度为32m，由东西看台组成，看台最大悬挑32m(图 2，图 3)，体型呈现开敞椭球形。该屋盖结构质量轻、柔性大，风荷载为控制屋面结构设计的主要荷载;同时，该结构位于大气边界层中处于风速变化大、湍流度高的区域，再加上屋面形状多不规则，《建筑结构荷载规范》中未规定对应可查询的风荷载体型系数，规范建议该类风荷载敏感的结构宜通过风洞试验确定体形系数。本文体育场为例，在风洞尚未进行的情况下，利用风数值模拟求得风荷载体型系数进行初步设计;在风洞试验进行之后，与风洞试验结果进行对比，分析数值模拟结果的精度和可靠性，探讨数值风洞的模拟方法和该结果用于初步设计的合理性。

2 数值模拟计算

2.1 风荷载数值模拟分析过程

图2 体育场建筑效果图图3体育场结构计算模型

a.根据研究对象的几何尺寸建立物理模型，确定计算流域的范围，保证流域足够大能消除边界对研究对象的影响。

b.根据实际情况选择合理的网格形式。

c.选择基本方程并根据研究的问题和需要的精度，确定所需要的湍流模型。

d.空气的相关参数的设定。

e.根据实际来流条件确定相应的边界条件。

f.根据求解精度的需要和促进迭代计算收敛的需要，调节各项的控制参数，收敛标准等。

g.计算和求解，进行迭代计算直至满足收敛标准。

h.检查结果，保存结果，如果结果不理想，还需要继续调整网格，改变数值和物理模型。

2.2 数值模型选择

本文数值模拟选用k－ε模型，压力与速度耦合方式为simple算法，收敛精度取值0.00013，经过计算，能够较好的收敛。

2.3 模型建立

主体育场模型以全尺寸模型建立，模型中心位于地面长轴方向距离风洞入口1/3处，计算域尺寸为长×宽×高为1500×1000×350m，网格采用非结构化网格，网格数量约为400万(图4、图5)。

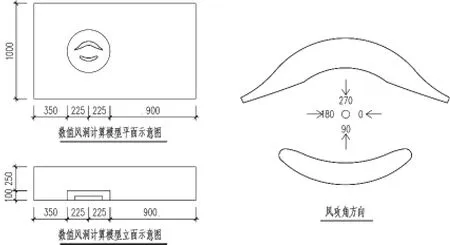
图4 计算模型示意图

2.4 边界条件设置

入口风剖面:

其中，μ1为垂直高度z位置的水平风速，μ0为参考高度 z0位置的风速;本工程数值模拟取值 μ0为 15m/s;本工程地面粗糙度为A类，故α取值为0.12。

湍流强度:

图5 计算模型局部图

zG取值为350m

壁面条件:

数值风洞表面和侧面采用自由滑移，壁面上速度为0。

出口条件:

出口位置认为湍流已经充分发展，沿流动方向没有变化，即为匀速，故各变量法向导数为0。

3 结果分析

3.1 数字模拟结果特性分析

各风向角下屋盖及其周围的整体的风压分布云图如(图6、图7)所示，可以看出，体育场屋盖主要受负压作用，尤其在边缘处局部负压较大。对于该大悬挑屋面分析其在各个风向下的风压分布，限于篇幅，本文取典型的0°和270°来 进行分析。

0°风向角时，即是风从东侧吹到西侧，顺着屋盖长的方向。该方向上南北悬挑屋盖表面风压分布规律大致相同，上表面为负压，下表面也为负压，上表面负压绝对值略大于下表面负压，上下叠加结果整体表现为负压;南北悬挑屋盖最大风压均出现在外边缘处，且边缘离风入口最近处风压最大;由于南北悬挑屋盖内侧边缘处趋于平缓，体育场屋盖为开敞结构，该位置风压接近为0。

图6 0°风向平均压力系数分布图

270°风向角时，即是风从北侧吹到南侧，垂直于屋盖长方向。该方向上南北悬挑屋盖表面风压分布沿着南北中心线呈现左右对称的规律，北悬挑屋盖上下表面风压均为负压，上表面负压绝对值较大，外边缘离风入口最近处风压最大，体形系数达到约－3.7，从外边缘到内边缘，风压梯度减小;南悬挑屋盖由产生兜风效应，故而上表面风压为负压，下表面风压为正压，上表面负压和下表面正压绝对值均也较小，整体表现为向上的吸力。

3.2 风洞试验结果简介

图7 270°风向平均压力系数分布图(数值模拟)

本工程委托中国建筑科学院风洞实验室进行试验，试验模型缩尺比例为1:200(图 8)，试验采用美国Scanlivalve公司最新的电子压力阀扫描系统DSm3400对模型表面进行平均和脉动压力测量，试验风速为15m/s，采样时间为21s。从风洞试验室提供的文本来看，数值模拟与之规律是一致的。

图8 风洞试验模型

4 数字模拟与风洞试验结果对比

4.1 结果对比

本文通过对风洞试验和数值模拟结果进行整理(图9～13)，分别对比屋盖中间大面积区域和边缘突变处两者风压体型系数数值的差异，结果见(表1)。

从(表1)对比可以看出，整体数值上来看，风洞试验结果大于数值模拟结果。具体到各个位置，除部分风压绝对值小于0.5区域以外，屋盖大部分区域两者偏差均在25%以内，误差最大为270度风攻角时的北悬挑屋盖外边缘处。

图9 0°风向平均压力系数分布图(风洞试验)

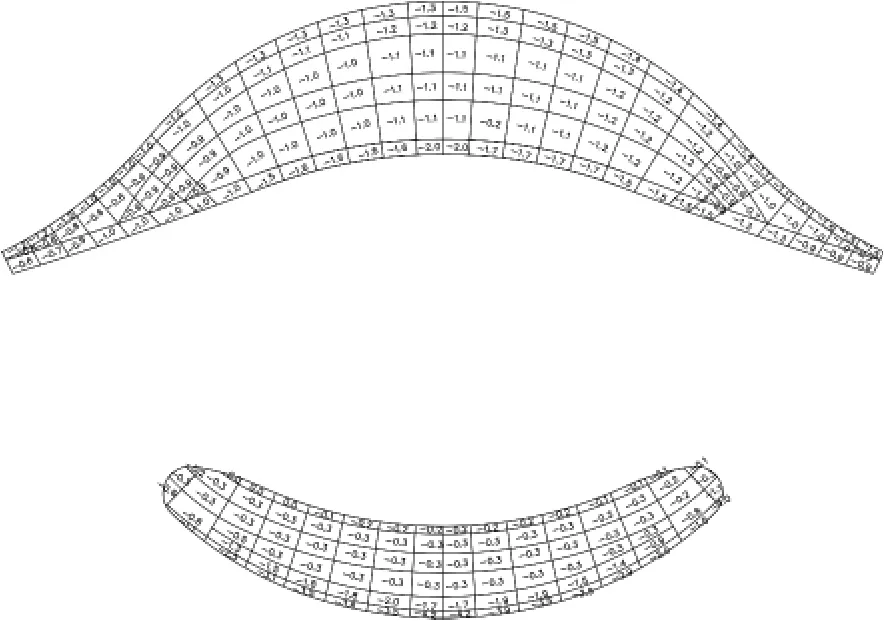
图10 90°风向平均压力系数分布图(风洞试验)

图11 0°风向平均压力系数分布图(数值模拟)

图12 90°风向平均压力系数分布图(风洞试验)

图13 数据整理网格图

表1 结果对比

4.2 误差分析

a.模型误差:体育场馆几何模型建模和网格划分难度较大，计算机的计算能力有限，模型不能建立得十分精确，计算时网格数量不能划分得足够精细，并且收敛误差取值0.00013略微偏大;

b.模型误差:边界条件不能完全吻合，入口的风剖面、粗糙度等不能完全模拟风洞试验的环境，导致流体在建筑物周围产生漩涡、分离等与试验有一定的差别，局部误差较大;

c.方法误差:数值模拟方法采用的是足尺度建模，而风洞实验采用的是几何相似、动力相似和来流条件相似的缩尺寸模型。

5 总结

(1)对海沧体育中心体育场风荷载进行数值模拟，并将体育场屋盖风荷载的数值模拟结果与已有的风洞试验数据进行比较，风荷载体型系数基本规律相同，屋盖中间大面积区域数值结果相近，虽然边缘处误差较大，但该位置面积较小，初步设计时虽然局部荷载计算不足，对整体结构指标影响不大，施工图阶段只需调整少数构件即可，从而说明数值模拟在初步设计阶段，作为结构设计的依据是可靠的。

(2)相比风洞试验，数值模拟具有以下几个特点和优势a.费用低，所需周期短、效率高;b.可以进行全尺度的模拟，能克服边界层风洞试验中难以满足雷诺数相似的困难;c.数值模拟方法有可视化的数据结果，可以提供风洞试验不便或无法提供的绕流流场信息。

(3)在风洞试验阶段，数值模拟结果对于风压测点布置具有一定的指导意义。

(4)通过对体育场风洞试验和数值模拟结果对比研究，发现对复杂大跨结构数值模拟精度有待进一步提高，特别是高负压处和边缘区域的局部误差较大。

[1]黄本才，汪丛军.结构抗风分析原理及应用[M].同济大学出版社.2008(2).9.

[2]孙晓颖，朱晓洁，武岳，等.深圳大运会主体育场罩棚风压分布的数值模拟[J].哈尔滨工业大学学报.2010.8.

[3]海沧体育中心风洞测压试验报告[D].中国建筑科学院.2012.2.