某工业化钢结构建筑动力特性的测试与分析

陈 颖

(福建省建筑科学研究院 福建福州 350025)

引 言

建筑工业化是建筑业发展的趋势之一，所谓建筑工业化是指将工业化生产的方式运用于建筑业生产，使建筑标准化、设计规范化、施工机械化、配套技术工厂化、管理科学化。目前国外发达国家已经建立了多种适合工业化建筑的成熟的结构体系，适合我国工业化建筑的结构体系正在完善、成熟中，工业化钢结构体系是我国建筑工业化结构体系中的一个重要分支。本文对某工业化钢结构建筑的周期、振型等动力参数进行实测，将实测结果与PKPM设计软件的计算结果进行比较，分析，为类似工程的测试和设计提供借鉴依据。

1 工程概况

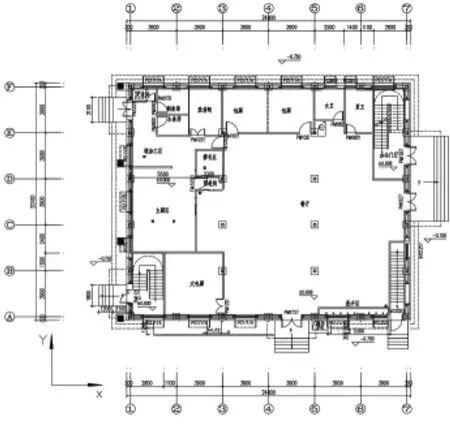
图1 一层建筑平面布置示意图

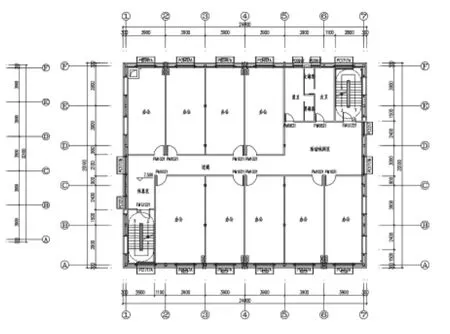
图2 三层建筑平面布置示意图

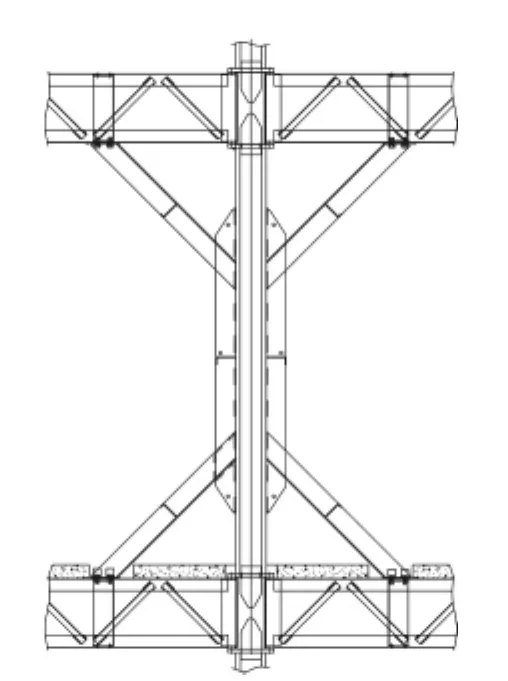
图3 边柱节点示意图

某综合楼一楼为厨房和餐厅，二、三、四楼为办公室，一层层高为4.2m，其余层层高均为3.3m，其中一层钢柱下设置高0.9m混凝土墩;结构形式为四层全螺栓现场拼装斜撑梁柱承重钢框架结构，基础采用预应力管桩。该结构的特点是在边角柱和主钢梁节点设置钢斜撑形成带斜撑梁柱，中柱与主钢梁节点为无斜撑梁柱节点，节点连接全部采用高强度螺栓连接。钢柱均为高3.3m方钢管柱，边长为200mm、壁厚为10mm，钢梁均采用格构式钢桁架梁，钢梁上铺设压型钢板浇筑混凝土形成主板架。该工程为工业化建筑，所有承重构件均在工厂预制完成后现场拼装完成，四层结构现场施工时间不到两天。具体建筑平面布置见(图1、图2)，节点示意见(图3、图4)，结构平面布置见(图5、图6)，测试时结构现状见(图7～图10)。

2 动力特性测试

本次测试采用脉动法测试，依次采用设置参数、采样、滤波编辑、分析、模态分析、示波的步骤。

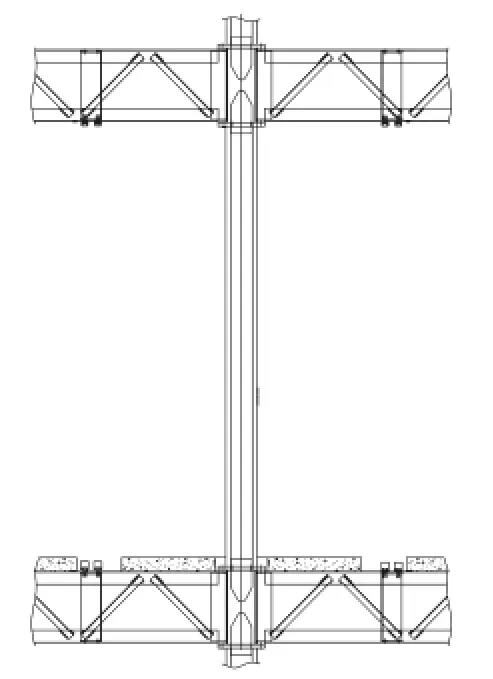
图4 中柱节点示意图

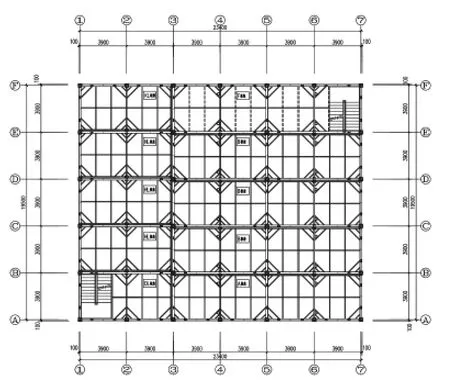
图5 二至四层结构平面布置示意图

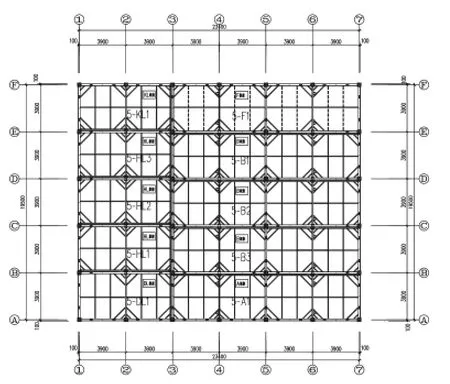
图6 屋面层结构平面布置示意图

图7 结构外观

图8 梁板结构

图9 中柱和主梁节点

图10 边柱斜撑

2.1 测点布置

为了消除结构扭转振动的影响，只获得建筑物的平移振动，应尽可能将传感器布置在建筑物的刚度中心。考虑到实际测试时刚度中心较难确定，本次试验在各楼层建筑几何中心各布置一个速度传感器，采用脉动测试法分别测量X、Y两个方向的水平振动，传感器布置于楼面上(图11)。

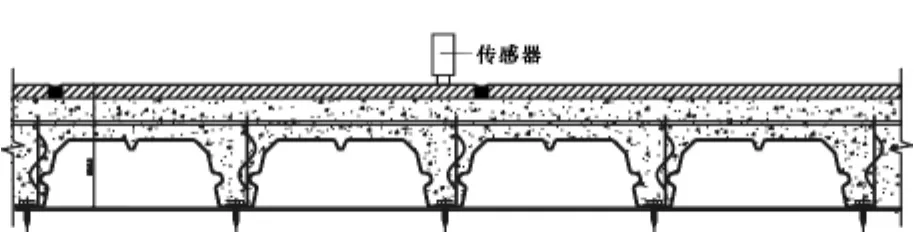
图11 传感器布置示意图

2.2 测试数据

本次测试采样频率为500HZ，运用输入未知时的结构模态参数识别的方法，对测试获得的时域记录进行离散傅立叶变换，从而获得各楼层质点在一定频带范围内的频谱曲线。(图12、13)分别为二层至屋面层X方向、Y方向自功率谱图。从图中可以看出，二层至屋面层X方向一阶固有振动循环频率均为 2.69HZ，自振幅值分别 0.0499、0.1095、0.1491、0.1759;Y方向一阶固有振动循环频率均为2.44HZ，自振幅值分别0.0429、0.0834、0.1343及0.1403。图14至图16为 X方向二层、三层，二层、四层，二层、五层互谱相干函数。从图中可以看出一阶相干函数分别为0.988、0.985、0.985，二阶相干函数分别为0.928、0.917、0.915;图17至图19为Y方向二层、三层，二层、四层，二层、五层互谱相干函数。从图中可以看出一阶相干函数分别为0.996、0.996、0.995，二阶相干函数分别为0.993、0.948、0.975，相干函数均接近1，表明二者具有良好的相关性，分辨得的自振频率是可靠的。

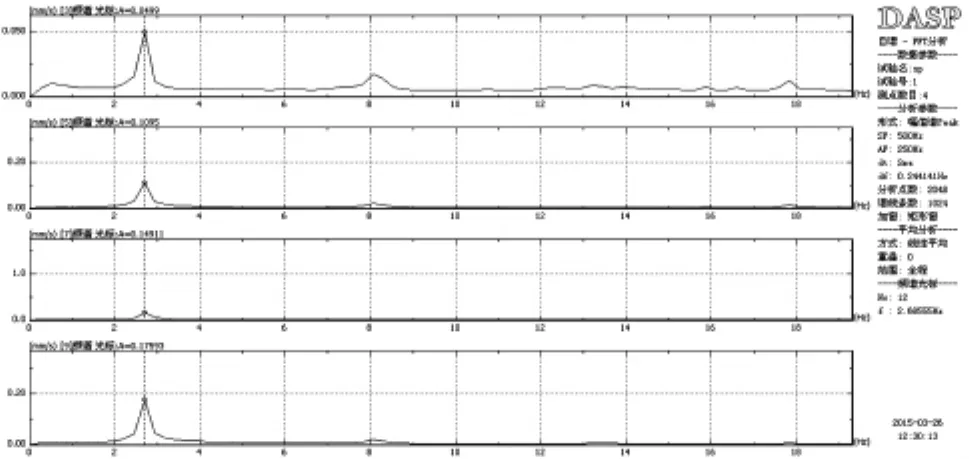
图12 X方向二层至屋面层自功率谱

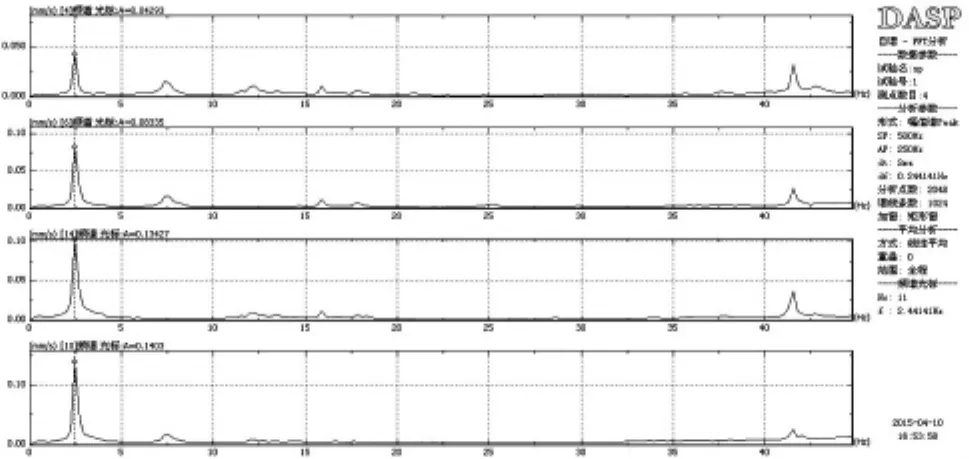
图13 Y方向二层至屋面层自功率谱

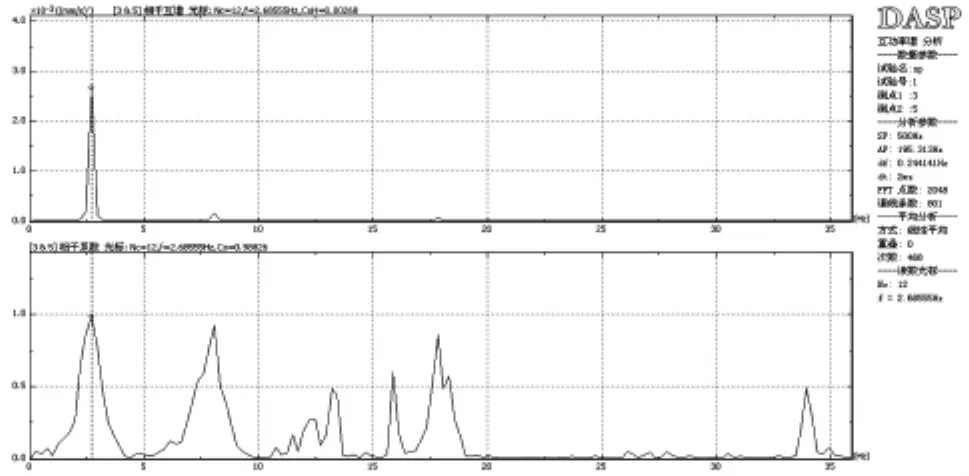
图14 X方向二层、三层互谱相干函数

2.3 测试的振型

多自由度结构具有阻尼比较小、各模态的频率相差大的特点，在任意激励作用下，振型比可以近似认为是在自振频率处相应信号的互谱与自谱的峰值比，由下式得出[1]:

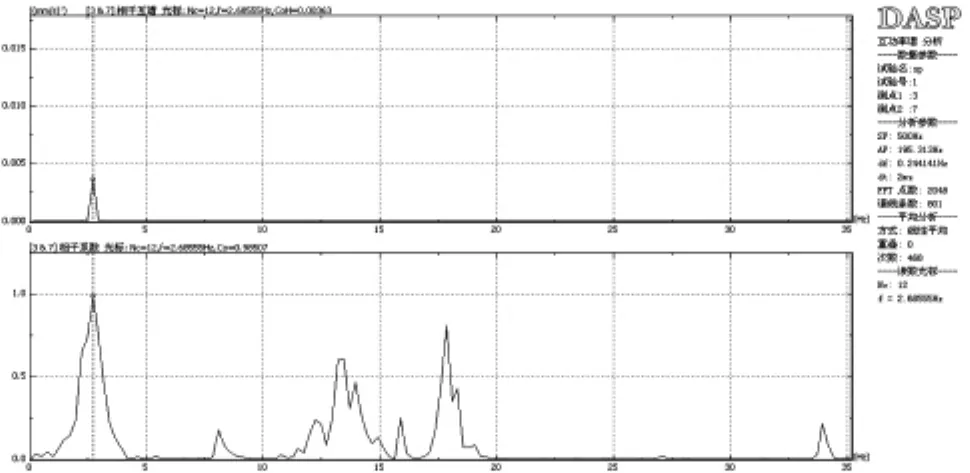
图15 X方向二层、四层互谱相干函数

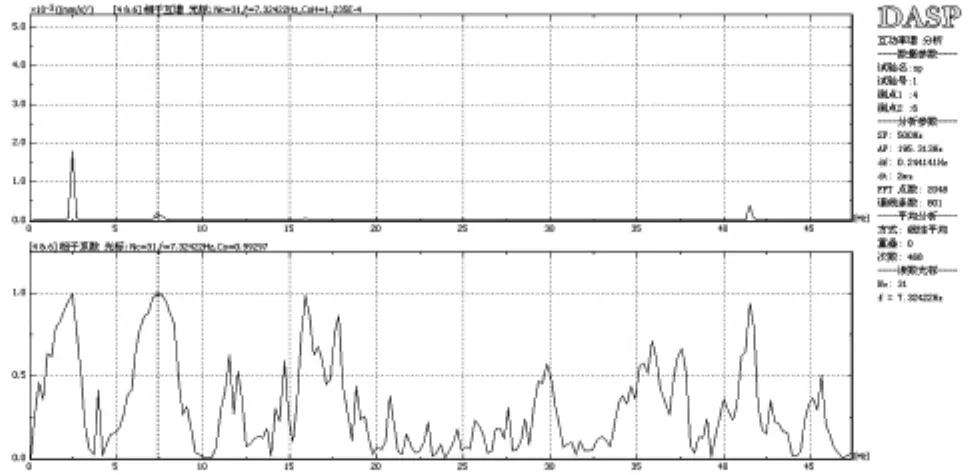
图17 Y方向二层、三层互谱相干函数

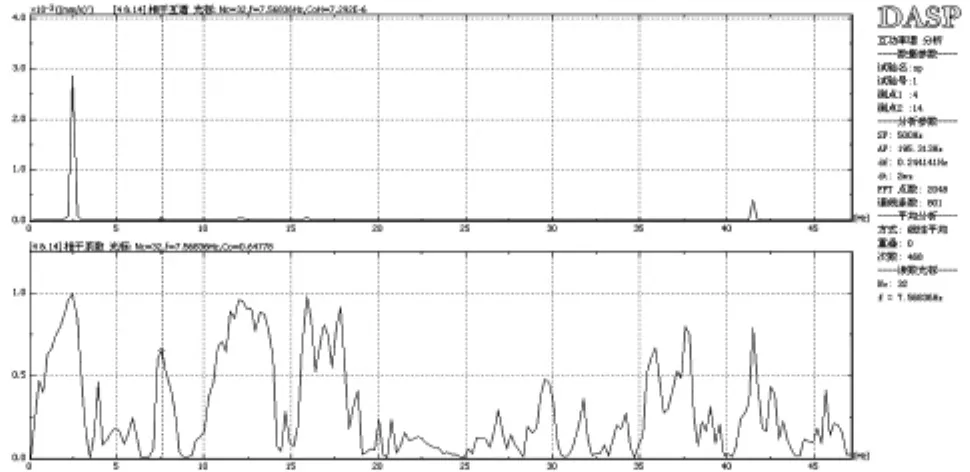
图18 Y方向二层、四层互谱相干函数

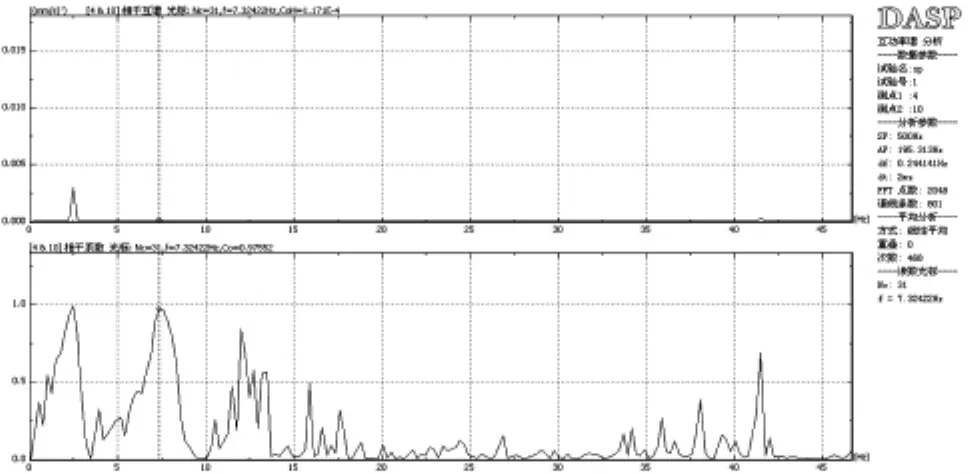
图19 Y方向二层、五层互谱相干函数

式中:Gapk(wi)为k、p测点的互功率谱，Gapp(wi)为p测点的自功率谱，φki，φpi分别为k测点、p测点的i阶振型的坐标。本次振动测试对应于波形图分析得到该建筑前两阶振型如(图20～图23)所示。

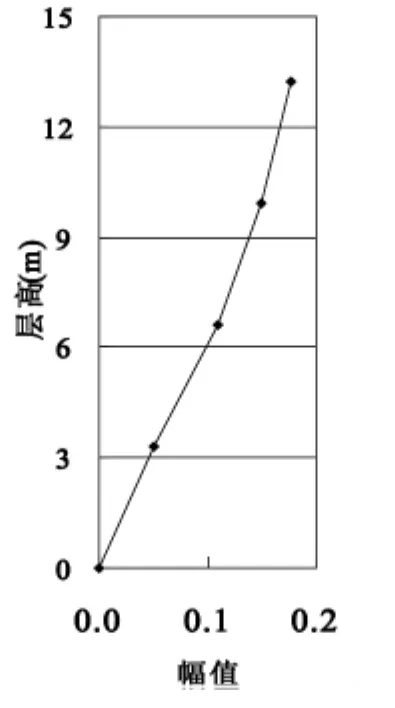
图20 X向一阶振型

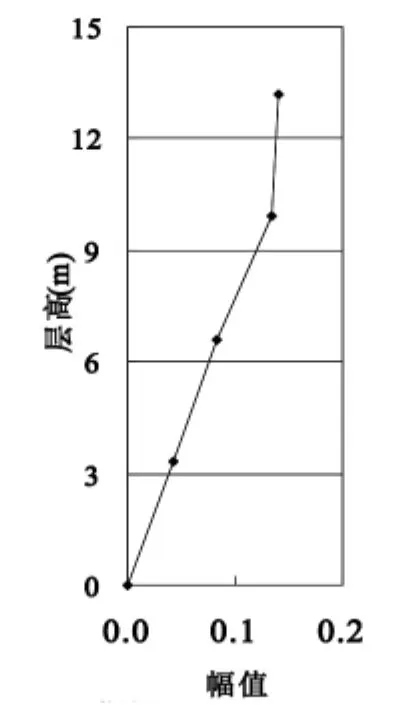
图21 Y向一阶振型

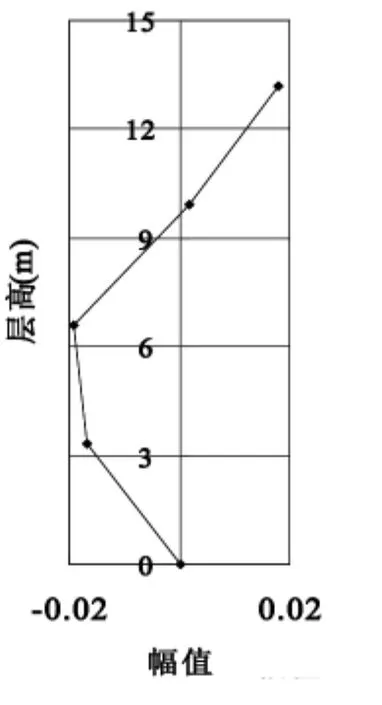
图22 X向二阶振型

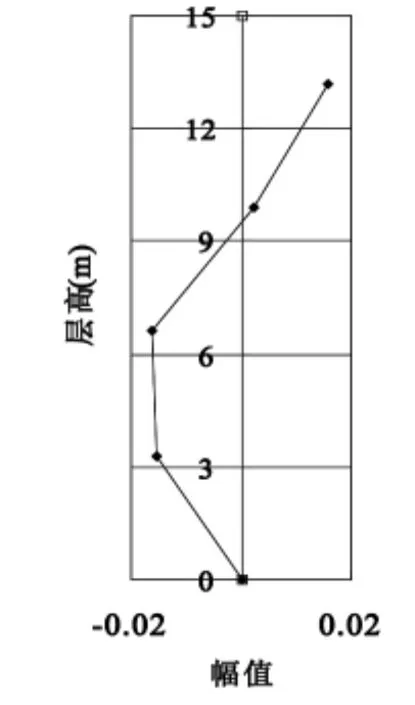
图23 Y向二阶振型

2.4 实测结果分析

X向、Y向前二阶振动特性列于(表1)。从(表1)可以看出，X方向第一阶振动频率较Y方向振动频率大，表明X方向结构抗侧刚度大于Y方向结构抗侧刚度，与实际结构刚度布置相吻合。各楼层在同一阶具有完全相同振动频率，这是由于工业化钢结构建筑为工厂模块化预制生产后现场拼装，保证了不同楼层梁柱构件、板构件、斜撑等尺寸偏差很小，节点施工方法有保障，工业化施工使建筑各楼层具有基本相同的刚度和质量，这也说明测试结果是可信的。

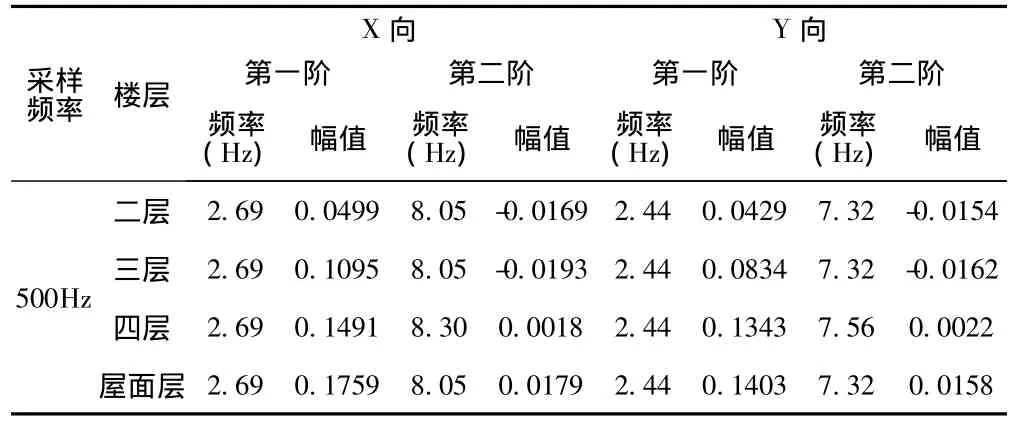
表1 工业化钢结构建筑X向、Y向前二阶振动特性

3 结构动力特性计算分析

3.1 模型的建立

由于目前没有专门为工业化建筑的设计软件，而设计人员普遍熟悉PKPM设计计算软件，本文采用PKPM软件建模计算该建筑的结构动力特性。由于PKPM软件中供用户选择的钢梁截面类型没有与该结构梁吻合的截面，本工程采用等效刚度及质量的等代梁模拟实际工程中的钢桁架，主梁与钢柱间的连接节点考虑为刚接、次梁同垂直相交主梁的连接节点考虑为铰接连接;边角柱与钢梁间的斜撑采用计算软件中的钢斜杆模拟，默认两端铰接，计算长度系数为1.0，并按轴心受力杆件进行验算，钢斜杆的模拟只考虑材料强度，未有具体截面尺寸设置。该钢结构建筑楼屋面板均为压型钢板混凝土组合板，为简化计算模型采用等质量原则将组合板折算为相同厚度混凝土楼板模拟。采用“一次性加载”对该建筑结构进行施工顺序模拟。为了与实测动力参数建筑仅施工完毕结构部分的现状相吻合，建模计算时不输入梁上荷载及楼屋面活荷载，其余荷载按相关规范取值[2]。

3.2 计算结果

(图24～图27)为PKPM软件计算结果输出的X、Y方向前两阶理论计算振型。PKPM软件计算结果看出该建筑第一振型号中Y方向的平动系数为1.00，相应平动振动周期为0.3513s，第二振型号中X方向的平动系数为1.00，相应平动振动周期为0.3298s。第三振型号对应扭转系数为1.00，相应扭转振动周期为0.2179s，第一扭转周期同第一平动周期的比值(Tt/T1)为0.62，小于规范0.9的限值[3]。上述计算结果表明该建筑在地震力作用下，第一阶振型分别为Y方向、X方向的平移振动，第三阶为扭转振动，对结构产生的能量中大部分只能够激起结构的平移振动，结构在两个主轴方向的动力特性较接近。X方向地震作用下及风荷载作用下的楼层最大位移分别为1/6158、1/5807，Y方向地震作用下及风荷载作用下的楼层最大位移分别为1/5442、1/4270，楼层最大位移均远小于规范要求[3]。

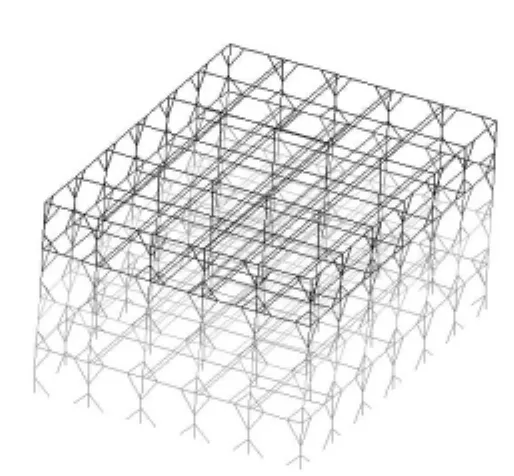
图24 X向一阶振型

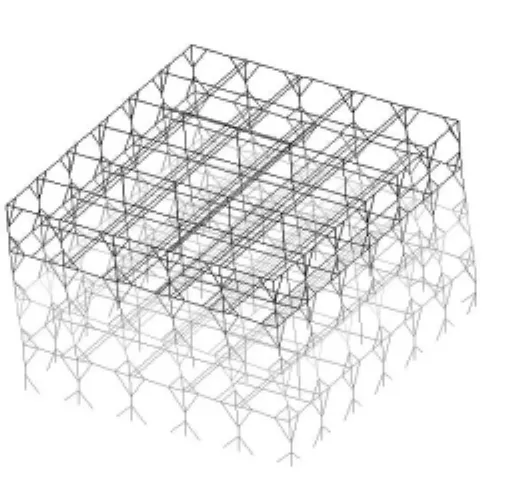
图25 Y向一阶振型

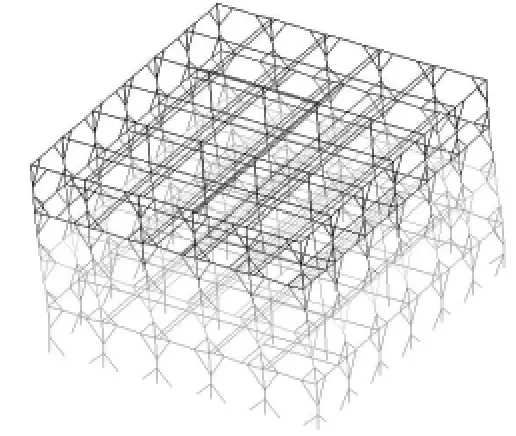
图26 X向二阶振型

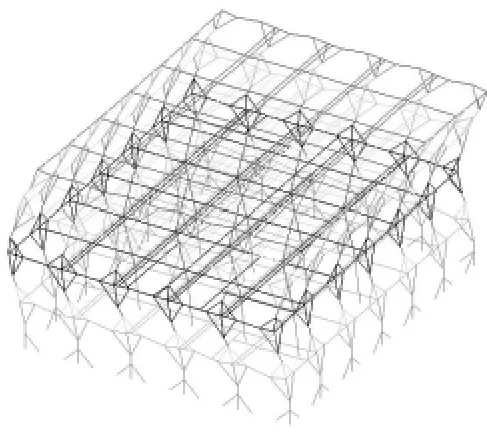
图27 Y向二阶振型

3.3 计算结果同实际测试比较分析

根据PKPM建模分析结果知X向平动振动周期为0.3298s，Y向平动振动周期为0.3513s。模型计算获得的平动振动周期约为实际测试结果0.89倍与0.86倍，二者基本吻合，且计算结果表明前两节振型均以平动为主，保证了结构在较小能量作用下不产生较大的扭转，这与测试时测点布置方案也是一致的。建模分析结果与实测结果产生偏差的主要原因是一层柱底同基础钢筋混凝土墩间尚未采用填料填实，柱底同基础连接方式介于铰接与刚接之间，这与计算模型中柱脚同基础设置为刚性存在不一致，(图28)为实际工程柱脚现状。另外PKPM建模分析中采用等效刚度及质量的等代梁模拟实际工程中的钢桁架梁，楼屋面压型钢板混凝土组合板简化为相同厚度混凝土楼板，及节点的刚接，铰接简化均对计算结果产生一定偏差。

图28 实际柱底现状

4 结论

(1)采用脉动环境试验的随机信号数据频域分析方法测试该种类型的工业化钢结构建筑的结构动力特性参数是可行的。通过测试结果说明各层具有几乎相同的刚度质量比，体现了该建筑钢结构工业化的特征。

(2)对于本文的具体工程项目，采用 PKPM建模分析，虽然经过一定的简化和假定过程，计算结果存在偏差，但是计算结果还是可以接受的。对于该种类型的工业化钢结构建筑如果采用设计软件计算分析时，应该确保简化和假定是正确可行的。

(3)该种类型的工业化钢结构建筑，还需要积累相关的测试数据并且努力探索符合本结构特征的计算方法。

[1]李斌，卢文胜，沈剑浩，等.高层建筑结构动力特性测试实例分析[J].结构工程师，2006，22(2):63 －67

[2]GB 50009－2012，建筑结构荷载规范[S].

[3]GB 50011－2010，建筑抗震设计规范[S].