基于MATLAB的管壳式换热器换热特性仿真

侯艳峰，刘 康，张 娜

（华北电力大学 能源动力与机械工程学院，河北 保定 071003）

0 概 述

换热器作为热力站能量控制系统中被控对象，是控制系统中的重要环节。换热器动态特性是分析、设计和改进换热器设备及其控制系统的重要依据［1，2］。只有了解换热器动态特性能，才能更好地对热力站能量控制系统进行调节，以达到更好的运行效果。MATLAB／SIMULINK是对动态系统进行建模、仿真和分析的软件包，具有模块化、可重载、可封装、面向结构图编程及可视化等特点，可大大提高系统仿真的效率和可靠性［3，4］

1 换热器的设计计算

管壳换热器的计算是一个较为复杂的过程。目前，比较流行的方法是对数平均温差法和NTU法。现采用无相变时管壳换热器的一般计算方法，该方法是以传热和压降准则关联式为基础的设计计算方法［5，6］。

针对某台油－水管壳式换热器进行设计研究，其设计参数为：将16t／h的煤油由140℃冷却到40℃，冷却水的进、出口温度分别为30℃、40℃，煤油侧的工作压力为0.1MPa，水侧的工作压力为0.3MPa。

根据竖直壁面的自然对流换热准则，水侧的努赛尔数：

式（1）中，水侧瑞利数：

水侧普朗特数：

水的热扩散率：

则水侧换热系数：

从而可得水侧的换热量：

根据管内湍流的迪图斯－贝尔特（Dittusboelter）公式，油侧的努赛尔数：

式（7）中，雷诺数：

油侧换热系数：

油至管壁的换热量：

式（1）～式（10）中：

cp1、cp2—水、油的定压比热，J／（kg·K）；

k1、k2—水侧、油侧的传热系数，W／（m2·K）；

A1、A2—水侧、油侧的换热面积，m2；

Thp—换热器金属壁面的平均温度，K；

l —特征长度，m；

υ1、υ2—分别为水、油的流速，m／s；

ν1、ν2—分别为水、油的运动黏度，m2／s；

Tf1、Tf2—分别为水流、壁面的平均温度，K；

Tw1、Tw2—分别为管内外壁面平均温度，K；

λ1、λ2、λ3—分别为水、油、管壁的导热系数W／（m·K）。

由上可知，换热器水侧的换热系数为941 W／（m·K）；油侧的换热系数为3 221W／（m·K）；换热面积为11.4m2；水的进口温度为303K；油的进口温度为413K。

2 求解传递函数与建立仿真模型

为建立传递函数做以下假定：

（1）由于工质的传热系数k1、k2随时间变化不大，可忽略不计。

（2）热交换在热流体、壁面以及冷流体的平均温度之间进行。

（3）传递函数的推导以管壳式换热器为分析对象来计算。

在换热器动态模拟过程中，当τ≤τ0时，x（τ）＝0；当τ≥τ0时，x（τ）＝x0。在一次阶跃扰动后所测出的某一个输出量随时间而变化的曲线称为阶跃响应曲线或飞升曲线［7，8］。

设线性定常系统微分方程的一般式为：

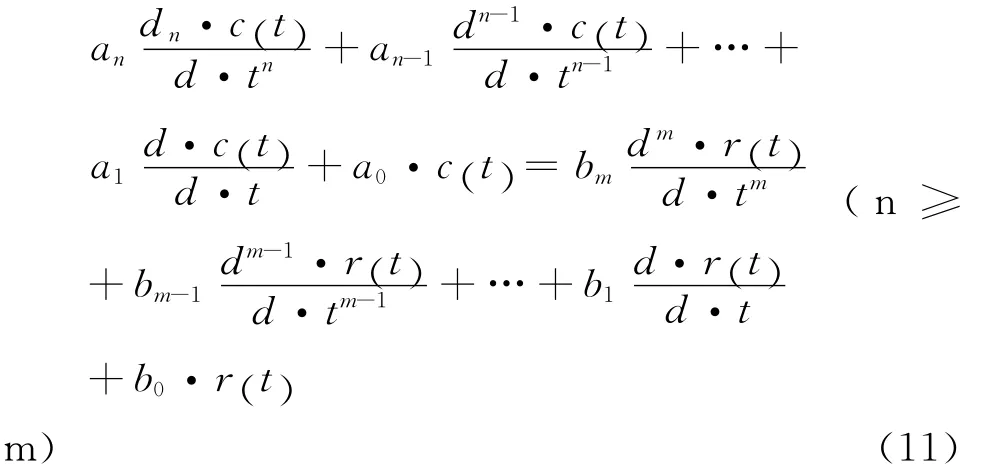
式（11）中，c（t）为输出变量；r（t）为输入变量；an、an－1、a1及a0为常量。设系统的初始条件为零，对式（11）取Laplace变换，得：

则系统传递函数为：

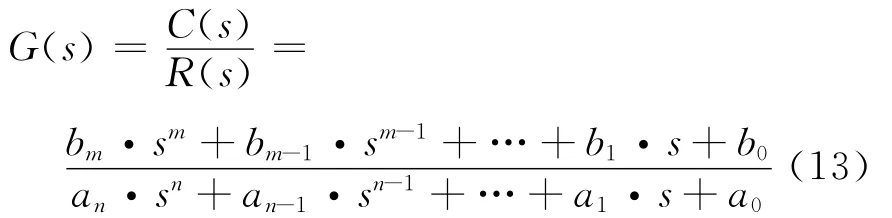
式（12）中，C（s）＝L［c（t）］；R（s）＝L［r（t）］；s为Laplace变换的运算子符号。

在上述简化假设的基础上，采用微元体的质量守恒方程、能量守恒方程、动量守恒方程、状态方程及工质管内流动方程，就可描述换热器的动态特性。微元体满足下列守恒方程：

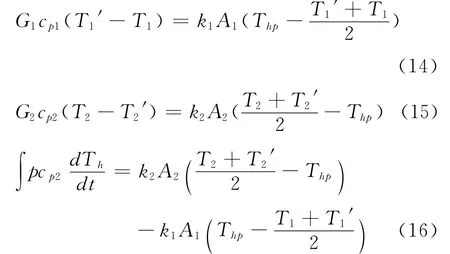
式（16）中：

G1—水的流量，kg／s；

G2—油的流量，kg／s；

T1、T2、T1′、T2′—水、油的进出口温度，K。

T1、T2变化时T＇2的响应尤为重要。所以采用增量方程消去中间变量Thp和T＇2，得到T1、T2与T＇2的关系式：

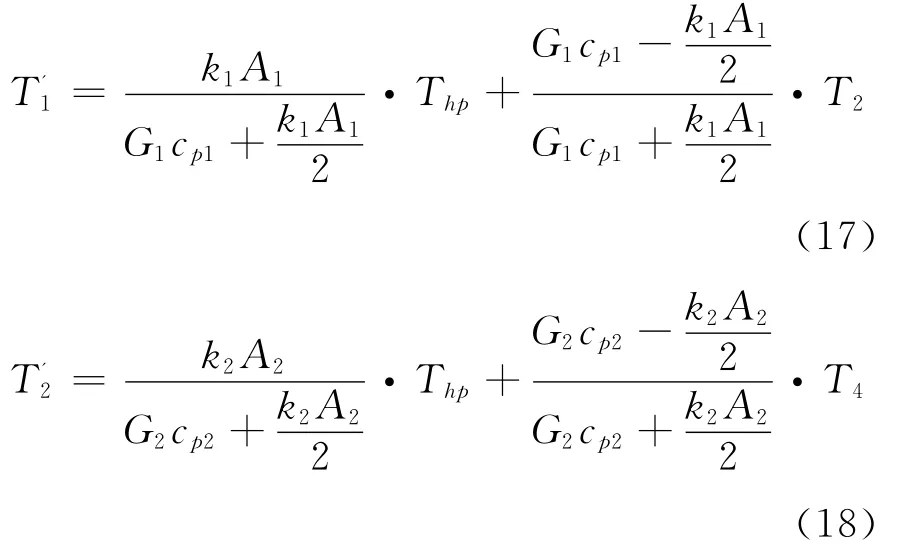
对于常规的换热器，可近似认为k1A1≈k2A2，G1cp1≈G2cp2。

式（17）、式（18）可写成：

，则式（19）、式（20）可简化为：

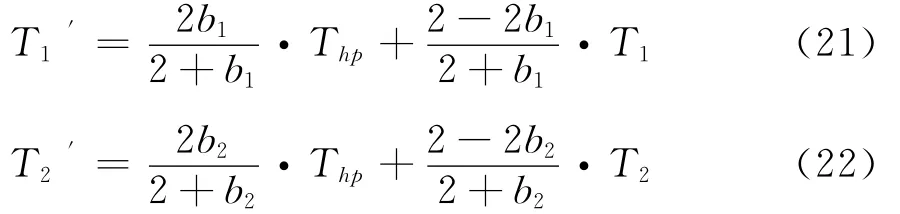
将式（21）、式（22）代入基本式（16）中，并写成增量形式：

对式（23）进行Laplace变换可得：

式（24）中：Thp、T1、T2为对应变量的Laplace变换，s为Laplace变换算子。

对T1′、T2′进行Laplace变换可得：

将（24）式代入上式（25）、式（26），若单独考虑水的进口温度分别对油出口温度的影响，水的进口温度对油的出口温度的影响传递函数：

同理，油的进口温度对出口温度影响的传递函数：

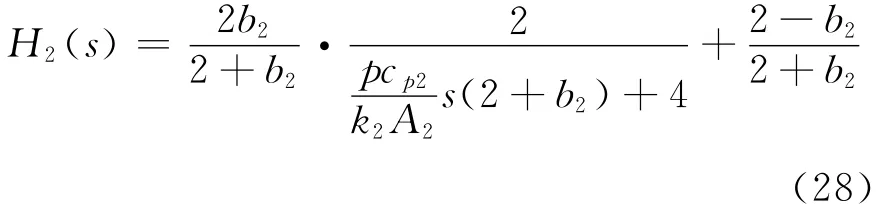
结合管壳式换热器的热力计算，且水的定压比热为4.179J／（kg·K）；油 的 定 压 比 热 为2.1 J／（kg·K）；

3 仿真模拟的实现

SIMULINK软件为用户提供了一个仿真与建模的通用工作平台。作为MATLAB软件的一个重要附属组件，SIMULINK具有准确、快速的特点。其可通过采用搭建模块的方法来创建动态系统的换热器模型，是一种强有力的仿真工具。根据传递函数，结合SIMULINK工具库，当热流体进口温度出现一阶跃扰动时，对冷流体出口温度影响的仿真程序，如图1所示。

图1 冷流体出口温度影响仿真框图（热流体进口温度扰动）

在MATLAB中运行这一程序框图，得到冷物流进口温度发生不同扰动情况时，对冷物流出口温度影响的仿真曲线，如图2、图3所示。

图3 热流体进口温度下降10K时冷流体出口温度仿真曲线

当冷流体进口温度有一阶跃扰动时，对冷流体出口温度影响的仿真程序，如图4所示。

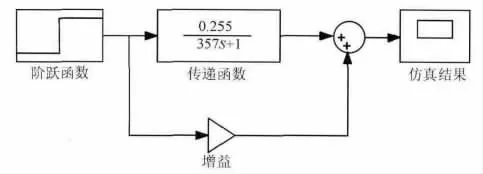
图4 冷流体出口温度影响仿真框图（冷流体进口温度扰动）

在MATLAB中运行这一程序框图，得到冷物流进口温度发生不同扰动情况时对冷物流出口温度影响的仿真曲线，如图5、图6所示。

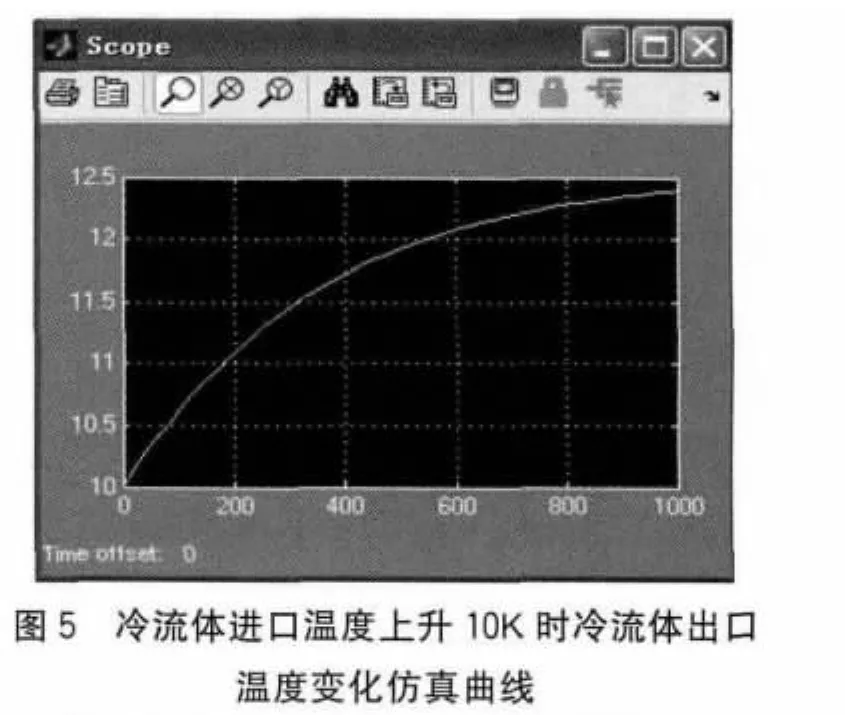
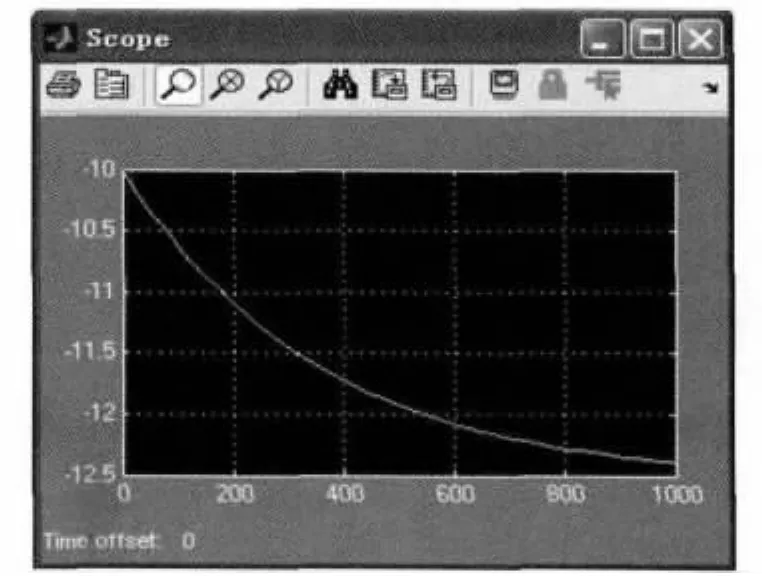
图6 冷流体进口温度下降10K时冷流体出口温度变化仿真曲线

4 结 语

经过软件的仿真模拟，可清楚地了解冷热流体入口温度出现阶跃性扰动时，出口温度的变化情况，仿真模拟的结果与现场实际情况相符合。根据仿真结果，设计合适的控制系统，从而减少控制过程的延迟，使控制系统更安全，更可靠。