置信规则库专家系统学习优化问题的研究

常瑞，白杨森，孟庆涛

(1．华北水利水电大学 电力学院，河南 郑州 450045;2．郑州新力电力有限公司，河南 郑州 450013;3．河南省预建工程管理有限公司，河南 郑州 450000)

在D －S 理论、决策理论和规则库的基础上，YANG 等［1］提出了基于证据推理方法的置信规则库推理方法(RIMER)．这是一种新的建模方法和专家系统，具有对带有含糊或模糊不确定性、不完整性或概率不确定性以及非线性特征的数据进行建模的能力．目前该方法广泛应用在故障诊断［2－3］、数据逼近［4］、输油管道的泄漏检测及漏油估计［5］、装备的寿命评估［6］等问题中． 但由于RIMER 专家系统容许专家直接人为设定置信度、规则权重、输入和输出的参考值等，而专家知识并不总是精确的，这就使RIMER 方法逼近函数的精度和能力降低． 因此，为提高系统的性能，需要对这些参数进行优化．YANG等［1］给出了优化训练模型，该模型是一个关于解决复杂的非线性高维优化问题的模型，已有多名学者针对该模型提出了不同的优化方法;并基于MATLAB 中FMINCON 函数针对置信度和规则权重进行了优化． 常瑞等［4］基于梯度法提出了参数训练方法，但是训练对象仅为规则的置信度以及规则权重，对参数的优化程度不足，因此降低了该系统模拟实际系统的能力． CHEN 等［7－8］将前提属性参考值作为新增的训练参数，之后采用MATLAB 中的FMINCON 函数对系统进行了优化训练．苏群等［9］提出了一种基于变速粒子群［10］的置信规则库训练方法．但是文献［7 －9］的训练参数中均不包含输出变量的参考值．吴伟昆等［11］在文献［4］的基础上提出了基于加速梯度法的置信规则库参数训练方法，训练参数包含了置信度、权重、前提属性参考值、输出参考值．但是该方法较为复杂，程序编写较为困难．

笔者在以上文献的基础上，训练除了置信度和规则权重外的优化参数，增加了输入和输出的参考值，根据训练参数的不同，将优化分为局部优化、局部扩展优化、全局优化，并且采用MATLAB 中的FMINCON 函数进行优化;基于RIMER 理论建立了发动机故障诊断系统，同时将该方法应用在了数据逼近中，通过实例研究参数的优化程度对系统性能的影响．

1 RIMER 基础理论

1．1 RIMER 中的知识表示方法

YANG 等［1］在传统IF-THEN 规则的结果部分引入分布式置信框架，提出了一种更接近实际的表达机制，称为置信规则．假设

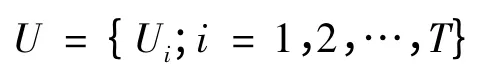
为规则前提属性的集合，而

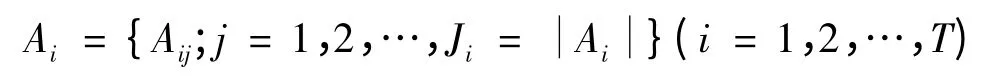
为前提属性Ui的参考值集合． 置信规则的形式如下:

Rk:IF U1is A1n1and U2is A2n2and…and UTis ATnT，

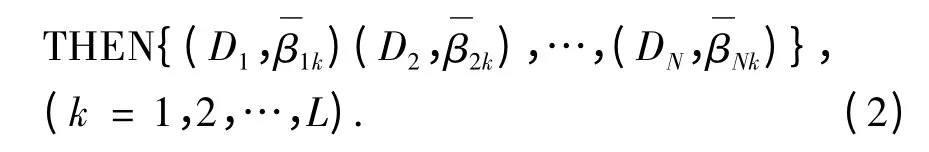
式中:Aini∈Ai(ni= 1，2，…，Ji)，为第i 个前提属性的第ni个参考值;Di为结果的第i 个参考值，该参考值可以为语义值也可为数字量;(i = 1，2，…，N)为结果，属于输出的参考值Di的置信度且有1;L 为规则库中规则的数目．

1．2 基于证据推理的置信规则库正向推理

步骤1 将输入信息转化为分布形式信息． 假设前提属性Ui的值为A*，其分布式形式表示为:

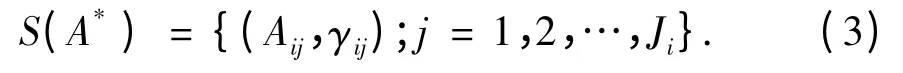
如果Aij≤A*≤Ai(j+1)，则

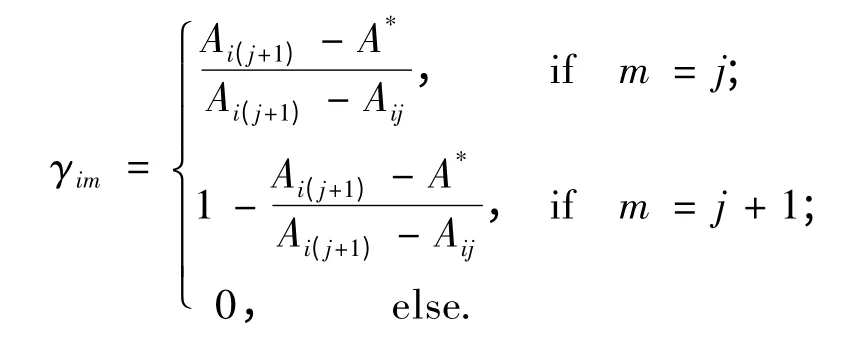
式中m = 1，2，…，Ji．

步骤2 激活规则． 当输入信息转化为分布式信息之后，规则库中的某些规则将被激活进入下一步的推理计算中．第k 条规则的激活权重为:

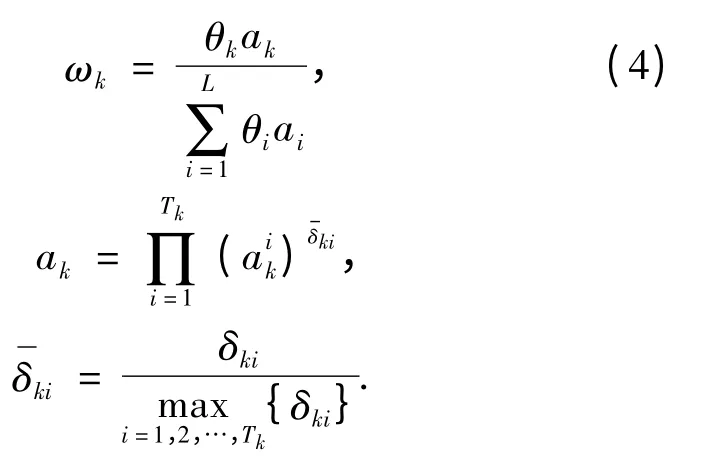
式中:θk为第k 条规则的相对权重;为第k 条规则中第i 个输入相对于参考值集合Ai的匹配度;δki为第k 条规则中第i 个前提的相对权重;ai为第i 条规则中输入变量相对于前提属性U 的整体匹配度;θi为第i 条规则的权重．

如果ωk＞0，表示第k 条规则被激活，否则第k条规则未被激活．

步骤3 集结规则，得到结果．在步骤1 和步骤2 的基础上，根据证据推理方法来集结被激活的规则，得到以分布式形式表示的结果，即

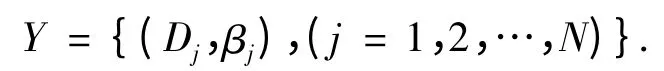
其中

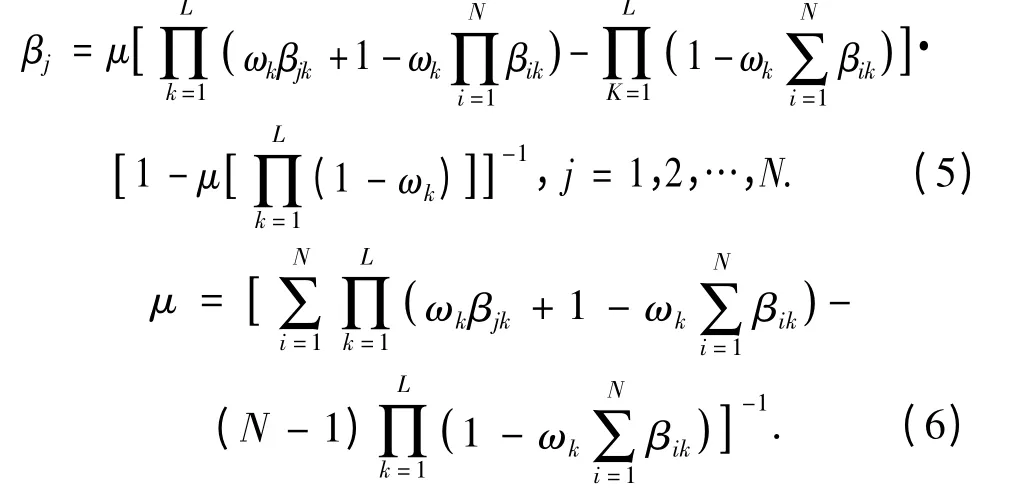
2 学习训练模型

RIMER 专家系统中规则的置信度、权重、前提属性和输出的参考值由专家知识初始给定，这就限制了该系统模拟实际系统的能力． 因此需要对该专家系统进行训练优化，以减小仿真系统和实际系统间的误差．训练优化过程如下:

步骤1 由初始专家知识确定规则置信度、权重、前提属性和输出结果的参考值，建立初始置信规则库．

步骤2 将输入数据转化为分布式形式．

步骤3 基于置信规则库和输入数据进行正向推理得到仿真输出，计算误差．

步骤4 如果误差在允许范围内，结束训练优化;否则，转步骤5．

步骤5 根据训练数据，通过MATLAB 中的FMINCON 函数实现对训练参数的优化，并且将优化结果保存，更新置信规则库，转步骤3．

假设共有M 组训练数据，在给定输入x^m(m =1，2，…，M)下，实际系统和模拟系统的输出有两种形式:

1)一种实际输出直接以分布式结果出现，即实际输出为:

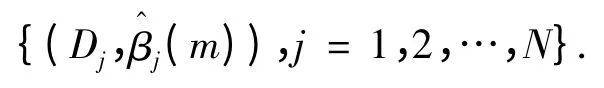
仿真输出为

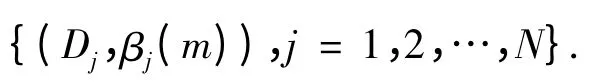
此时，训练模型的目标函数定义如下:

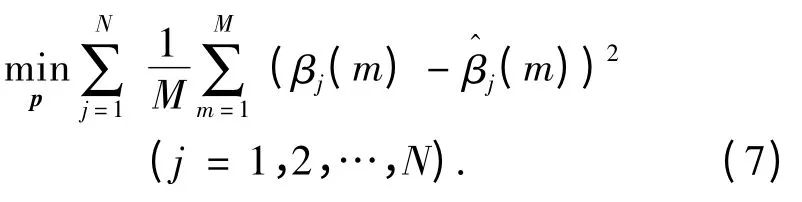
式中p 为训练优化参数向量．

由于此时输出为分布式形式，输出变量的参考值为固定值，不需要进行优化训练，因此训练参数向量

p = p(θk，βik)或p = p(Aij，θk，βik)．

式中:βik(i = 1，2，…，N;k = 1，2，…，L)为第k 条规则中结果属于参考值Di的置信度;θk(k = 1，2，…，L)为第k 条规则的权重;Aij为第i 个输入变量的第j个参考值．优化参数应满足的约束条件为:

①置信度满足:

0 ≤βjk≤1;j = 1，2，…，N;k = 1，2，…，L．

②置信度的和应满足:

③规则权重满足:

0 ≤θk≤1;k = 1，2，…，L．

④假设输入变量xi(i = 1，2，…，T)的定义域为［ai，bi］．前提属性参考值Aij(i =1，2，…，T;j =1，2，…，Ji=)应满足:

ai≤Aij≤bi．

不失一般性，假设前提属性参考值依次增大，即:

Aij－ Ai(j+1)＜0

(i = 1，2，…，T;j = 1，2，…，Ji－1)．

图1 为RIMER 专家系统学习优化的过程示意图．

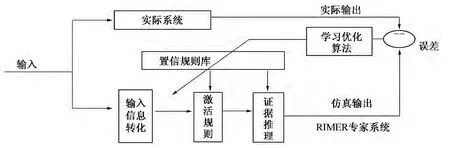
图1 置信规则库的训练优化过程

当目标函数为公式(7)时，训练参数向量

p = p(θk，βik)，

即训练参数为权重和规则置信度，并且满足约束条件①—③时，称为局部优化;训练参数向量

p = p(Aij，θk，βik)，

即训练参数为输入的前提属性权重、置信度，并且满足约束条件①—④时，称为全局优化．

2)另外一种是实际输出以数字量y^m的形式出现，此时需将RIMER 专家系统经过正向推理得到的仿真结果

{(Dj，βj(m))，j = 1，2，…，N}

转化为数字量的形式:

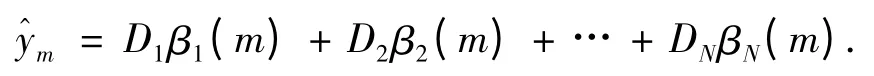
此时，训练模型的目标函数定义如下:

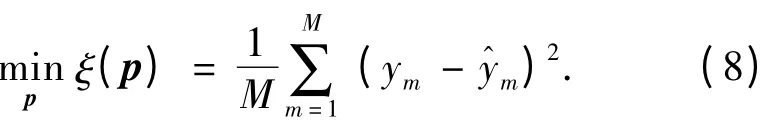
式中p 为训练优化参数向量，p = p(θk，βik)、p =p(Aij，θk，βik)或p = p(Aij，Hn，θk，βik)，其中βik、θk和Aij与前面所述意义相同，Hn(n = 1，2，…，N)为输出的第n 个参考值．

训练优化参数除了应满足约束条件①—④外，还应满足第5 个约束条件:

⑤假设输出的值域为［c，d］．因此，当输出参考值Dj为数字量时，应有输出参考值保持依次增大的顺序，即

c ≤Dj≤d(j = 1，2，…，N)，

Dj－ Dj+1＜0(j = 1，2，…，N －1)．

另外，前提属性、输出的第一个和最后一个参考值在训练优化中如果偏离其上限和下限，即使只有很小的偏差，也会影响仿真系统的精度，故设定前提属性、输出变量的第一个和最后一个参考值分别为其上限和下限，即:

Ai1= ai， AiJi= bi，

以及D1= c， DN= d．

当训练目标为公式(8)时，训练参数向量

p = p(θk，βik)

满足约束条件①—③时，称为局部优化;训练参数向量

p = p(Aij，θk，βik)

满足约束条件①—④时，称为局部扩展优化;训练参数向量

p = p(Aij，Hn，θk，βik)

满足约束条件①—⑤时，称为全局优化．

3 实 例

3．1 基于RIMER 专家系统的发动机故障诊断

系统

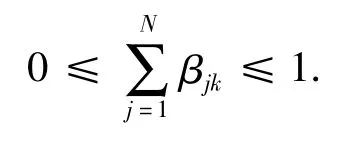
假设发动机故障诊断中有3 个前提属性，分别为进气压力、转速、喷油时间． 发动机的4 种工作状态为正常怠速、进气系统漏气、怠速电机不工作和某缸喷油器堵塞．每个前提属性分为3 个评价等级，即进气压力分为{高，正常，低}，转速为{高，正常，低}，喷油时间{长，正常，短}，对应的参考值分别为:

{39．9，33．8，23．8}，

{1982．2，896．3，848．9}，

{5．5，3．6，1．5}．

正常怠速、进气系统漏气、怠速电机不工作和某缸喷油器堵塞所对应的输出代码分别为:

{1 0 0 0}，{0 1 0 0}，

{0 0 1 0}，{0 0 0 1}．

根据以上设定的评价等级及输出代码，根据发动机的怠速工作原理，建立关于怠速状态的故障诊断规则库，初始置信度由专家给定．由于文中选取3个前提属性，每个前提属性有3 个评价等级． 因此，在RIMER 中包含27 条规则，具体规则见文献［3］．

本实例中的输出结果为分布式，因此不需要对输出的参考值进行优化．采用MATLAB 中的FMINCON 函数对发动机故障诊断系统的参数进行优化，其中文中的训练数据和检验数据与文献［3］中的相同．对专家系统进行优化后，基于检验数据得到系统的仿真输出，与文献［3］中的输出结果进行比较，比较结果见表1．

表1 局部优化和全局优化后RIMER 专家系统输出结果比较

从表1 中可以看出，相同输入下，本文采用FMINCON 函数进行优化时，不论是全局优化还是局部优化均取得了比文献［3］更精确的诊断结果． 另外，与局部优化相比，总体上全局优化后系统的诊断结果更准确．这意味着对参数的优化程度越深，系统越能更好地模拟实际系统．

以第2 组数据为例，当进气压力为34．1 kPa，转速为904．1 r/min，喷油时间为3．4 ms 时，实际的发动机状态为正常怠速，局部优化和全局优化的仿真结果分别为:

{0．982 8，0．006 9，0．000 4，0．009 9}，

{0．991 5，0．002 9，0．000 7，0．004 9}．

由仿真结果知:发动机故障类型为正常怠速的可能性分别为0．982 8和0．991 5，进气系统漏气的可能性分别为0．006 9 和0．002 9，怠速电机不工作的可能性分别为0．000 4 和0．000 7，某缸喷油器堵塞的可能性分别为0．009 9 和0．004 9．该试验结果表明了每种故障的可能性，可为维修人员查找故障原因提供参考．

3．2 数据逼近实例

以二元函数

z=(x+1)2+(y－1)2

为例进行数据逼近． 假设输入x 的取值范围为［0，2］，初始确定5 个参考值

{0．0，0．5，1．0，1．5，2．0};

输入变量y 的范围为［－1，1］，初始确定5 个参考值

{－1．0，－0．5，0．0，0．5，1．0};

输出z 的范围为［1，13］，初始确定6 个参考值

{1，3，4，6，9，13}．

建立的置信规则库见表2，共有5 ×5 =25 条规则．

表2 初始置信规则库

置信规则库建立完成之后，选

x=0．05，0．10，1．95，

y= －0．95，0．10，0．95

为检验数据，基于初始置信规则库完成正向推理，得到RIMER 专家系统的输出，如图2 所示．计算得到系统的平均绝对误差为0．439 9．

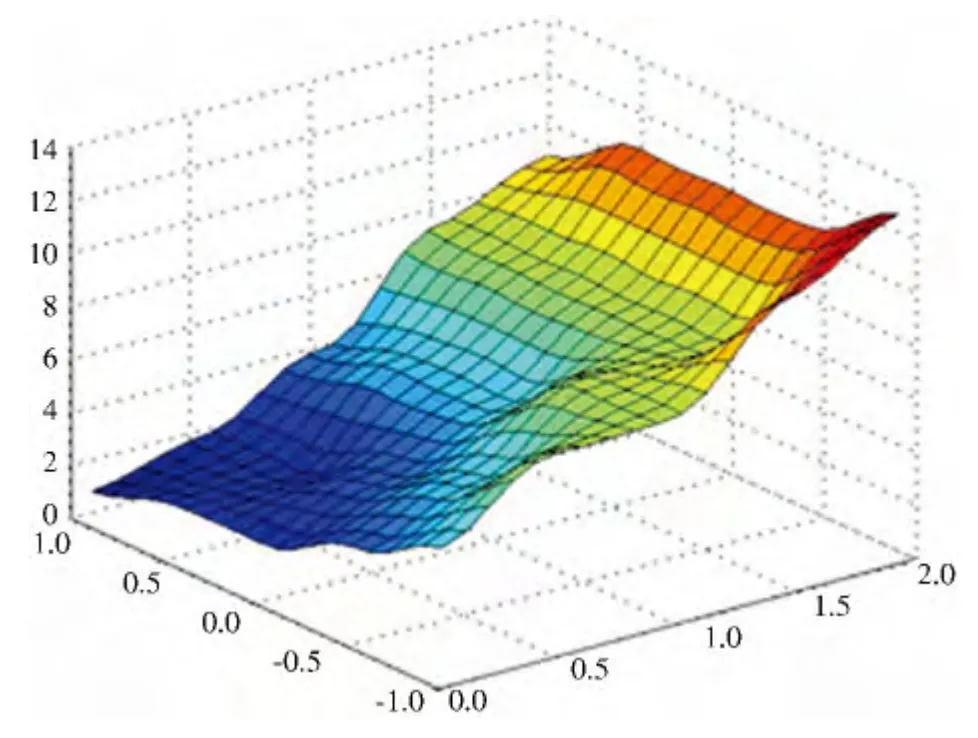
图2 训练前RIMER 专家系统的输出

从图2 以及此时的平均误差可知，未训练的专家系统的推理结果与实际结果间总体上误差较大，因此，有必要对该置信规则库进行训练学习．

选输入

x=0．0，0．1，2．0，

y= －1．0，0．1，1．0．

相应的输出

z=(x+1)2+(y－1)2

为训练数据．局部训练时，以规则的权重θk(25 个)和置信度βik(150 个)构建训练参数向量

p=p(θk，βik)(175 维)．

局部扩展训练时，以2 个输入变量x、y 的输入参考值A1n1(5 个)和A2n2(5 个)，规则权重θk和置信度βik构建训练参数向量

p=p(A1n1，A2n2，θk，βik)(185 维)．

全局训练时，以2 个输入变量x、y 的输入参考值A1n1和A2n2，输出变量z 的输出参考值Hn(6 个)，规则权重θk及置信度βik构建训练参数向量

p=p(A1n1，A2n2，Hn，θk，βik)(191 维)．

局部扩展优化后输入x 的参考值

{0，1．027 8，1．150 7，1．265 5，2}，

输入y 的参考值

{－1，－0．433 5，－0．246 4，－0．054 3，1}．

全局优化后输入x 的参考值

{0，0．927 3，1．132，1．269 2，2}，

输入y 的参考值

{－1，－0．337 3，－0．144 4，0．133 9，1}．

全局优化之后输出z 的参考值

{1，1．489，3．054，5．574，9．363，13}．

置信规则库优化完成之后，选

x=0．05，0．10，1．95，

y= －0．95，0．10，0．95

为检验数据，基于3 种优化训练下的置信规则库完成正向推理，得到RIMER 专家系统的输出，图像和误差分析结果如图3—5 所示．

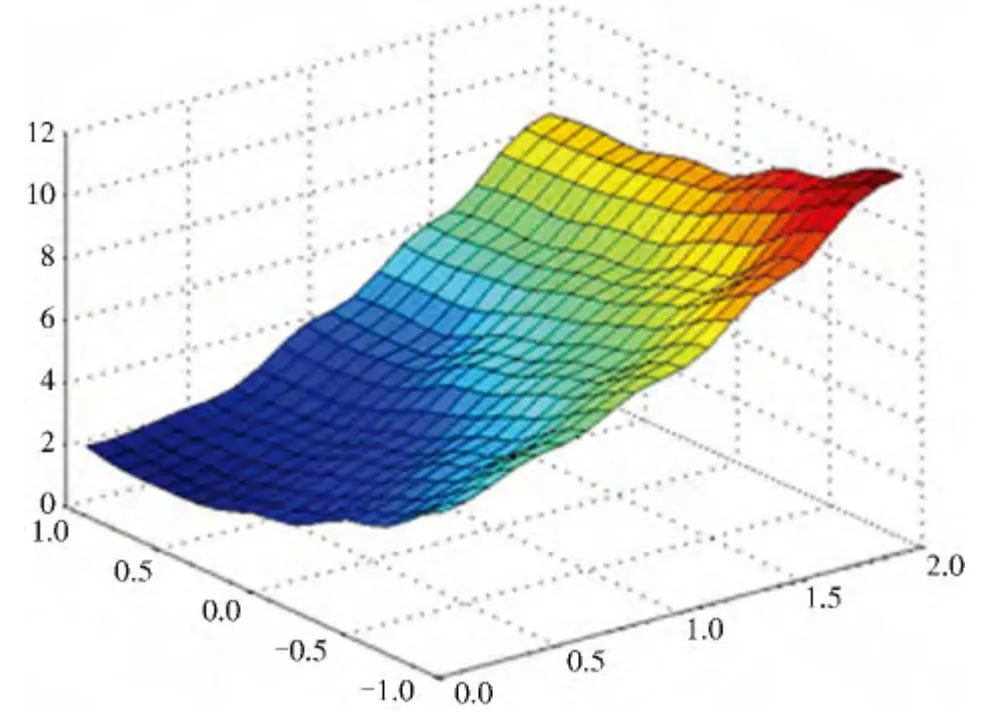
图3 局部训练后RIMER 专家系统的仿真输出

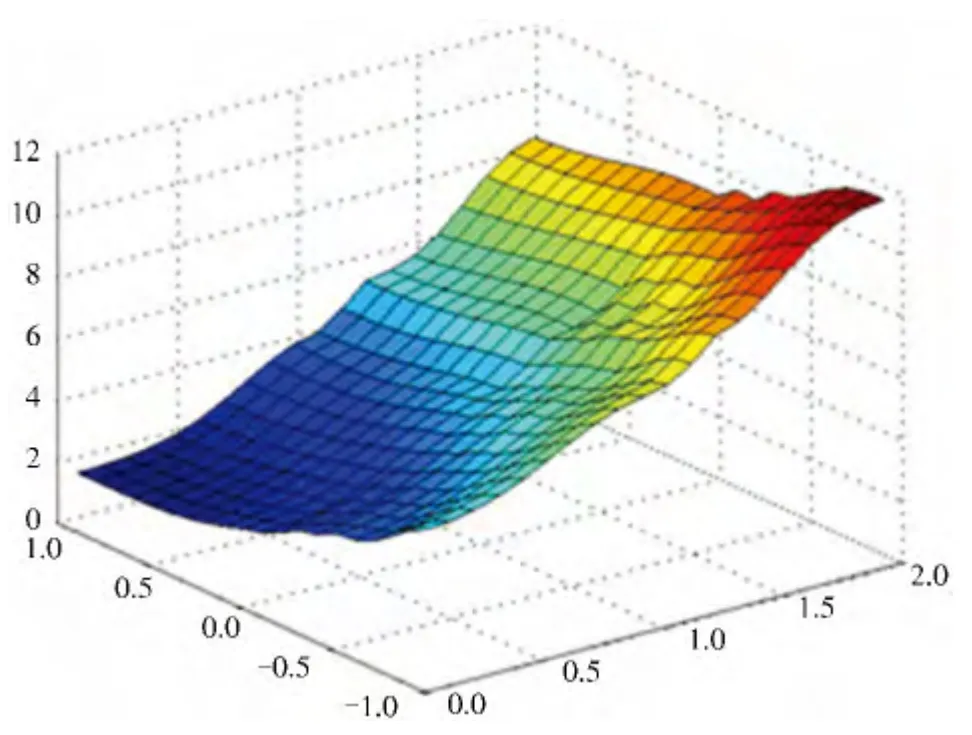
图4 扩展局部训练后RIMER 专家系统的仿真输出

对比分析图3—5，虽然训练后仿真系统和实际系统间还有一定的误差，但是计算得到局部优化、局部扩展优化、全局优化后系统的平均绝对误差分别为0．035 2、0．024 5、0．022 8，与训练前的平均绝对误差值0．439 9 相比，优化训练后仿真系统和实际系统间的结果差异得到了很大的改善，仿真精度得到了提高，这就表示，经过学习训练的专家系统可以很好地模拟仿真原系统．另外，从平均绝对误差可以看出，对训练参数的优化越深，即全局优化后的系统的误差越小，这就表示全局优化的RIMER 系统能够更好地模拟实际系统，这与3．1 节的结论一致．

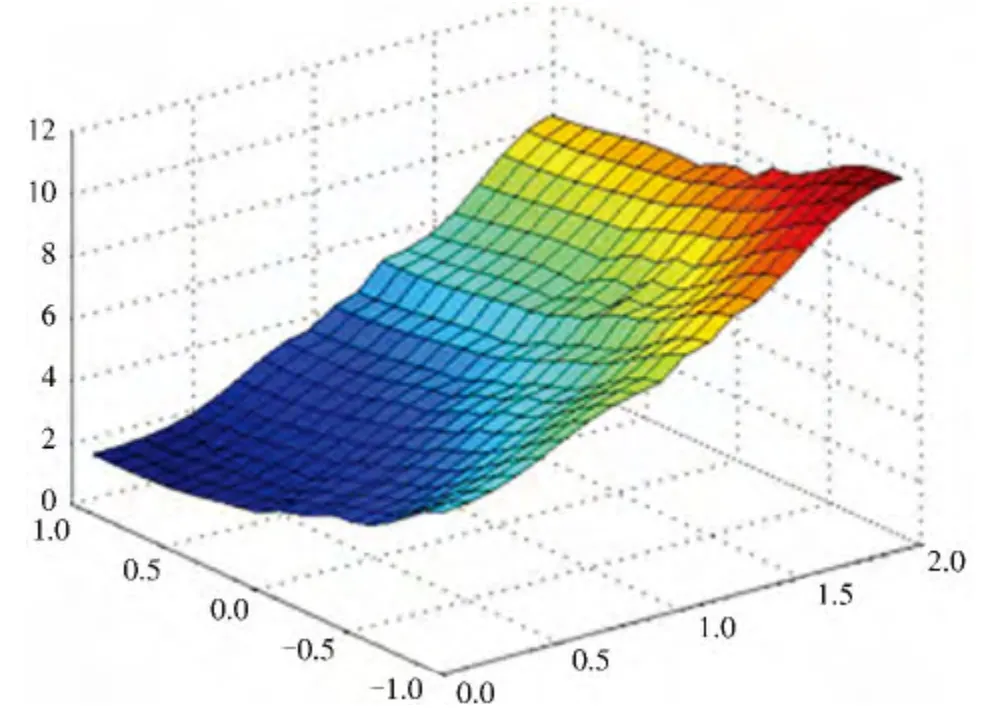
图5 全局训练后RIMER 专家系统的仿真输出

4 结 语

针对目前对RIMER 专家系统参数优化训练不够的现状，根据对专家系统的参数训练程度将优化分为局部优化、局部扩展优化、全局优化． 在试验分析中，将RIMER 理论应用在发动机故障诊断和数据逼近中，并采用FMINCON 函数对其系统进行了优化训练．结果表明，对参数的优化程度越深，RIMER系统的精度越高．未来可针对全局优化参数较多的情况，寻找精度更高、速度更快的算法来提高系统模拟实际系统的能力．

［1］YANG J B，LIU J，WANG J，et al．An generic rule-base inference methodology using the evidential reasoning approach-RIMER［J］． IEEE Transactions on Systems，Man and Cybernetics-part A:Systems and Humans，2005，14(2):1 －20．

［2］张邦成，尹晓静，王占礼，等．利用置信规则库的数控机床伺服系统故障诊断［J］． 振动、测试与诊断，2013，33(4):694 －700．

［3］张伟，石菖蒲，胡昌华，等． 基于置信规则库专家系统的发动机故障诊断［J］． 计算机仿真技术，2011，7(1):11 －15．

［4］常瑞，张速．基于优化步长和梯度法的置信规则库参数学习方法［J］． 华北水利水电学院学报，2011，32(1):154 －157．

［5］XU D L，LIU J，YANG J B．Inference and learning methodology of belief-rule-based expert system for pipeline leak detection［J］． Expert Systems with Applications，2007，32(1):103 －113．

［6］刘佳俊，胡昌华，周志杰，等．基于证据推理和置信规则库的装备寿命评估［J］．控制理论与应用，2015，32(2)，231 －238．

［7］CHEN Yuwang，YANG Jianbo，XU Dongling，et al． Inference analysis and adaptive training for belief rule based systems［J］． Expert Systems with Applications，2011，38(10):12845 －12860．

［8］CHEN Yuwang，YANG Jianbo，XU Dongling，et al． On the inference and approximation properties of belief rule based systems［J］．Information Sciences，2013，234:121 －135．

［9］苏群，杨隆浩，傅仰耿，等．基于变速粒子群优化的置信规则库参数训练方法［J］． 计算机应用，2014，34(8):2161 －2165．

［10］熊俊华，沈海莲，吴莉莉，等． 求解自动化药房储位优化问题的GA－PSO 混合粒子群算法［J］．华北水利水电大学学报(自然科学版)，2014，35(6):84 －88．

［11］吴伟昆，杨隆浩，傅仰耿，等． 基于加速梯度法的置信规则库参数训练方法［J］．计算机科学与探索，2014，8(8):989 －1001．