霞曲流域1956—2010年降水趋势分析
刘增进,李东琴,,张海涛,刘妞,,刘宁
(1.华北水利水电大学 水利学院,河南 郑州 450045;2.中国水利水电科学研究院水资源所,北京 100038)
易贡藏布江的左岸支流称为霞曲,发源于西藏自治区边坝县金岭乡僧达隆以西的嘎卜拉山,位于东经93°33'—94°36'、北纬30°24'—30°54'. 霞曲流域面积为2 952 km2,河长82 km,落差1 990 m,蕴含丰富的水电能源,流域内主要涉及西藏自治区的边坝县.
霞曲流域多年平均降水量800 ~2 000 mm,分属2 个降水带.年降水量从东南向西北逐渐减少,降水量最大的区域位于东南部一带,年降水量超过1 800 mm;降水量最小的是西北区域,年降水量不足1 000 mm.流域多年平均径流量约35.4 亿m3,多年平均流量约112 m3/s,干流水力资源理论蕴藏量约33.56 万kW.目前,西藏水资源尚未开发,自然生态环境保持完好,水资源开发利用程度比较低,工程性缺水比较严重.近些年,西藏地区在保护地区水生态环境的基础上,加大了中小型河流的规划.霞曲流域开发利用的水资源量供不应求,已严重影响到当地居民生活与经济的发展,因此,研究霞曲流域降水量的变化规律具有重要意义.
笔者基于霞曲流域周边站点1956—2010 年的降水资料,采用ARCGIS 软件进行空间插值获取霞曲流域资料,再利用Mann -Kendall 检验法、滑动平均法、累计距平法、小波分析法等对该流域降水量进行系统地分析,为该流域的水资源综合规划以及合理开发利用提供参考.
1 研究方法
目前,针对降水趋势性分析的方法[2-5]有很多,如累计距平法、线性倾向估计法、Mann -Kendall 检验法、Spearman 秩序相关检验法、小波分析法等. 线性倾向估计法的优点是可以定性分析趋势性变化,并对序列数据进行显著性检验;Mann-Kendall 检验法的优点[6]是序列数据不需要遵循某种分布,同时也几乎不受异常值的干扰,计算过程比较简单;累计距平法能根据曲线上下起伏的变化来判断其长期的演变趋势及持续性变化,得到突变点的时间;小波分析法[7-8]适用于研究水文及水资源多时间尺度变化规律,弥补传统方法仅能分析单一时间尺度规律的不足,基于Fourier 变化功能基础,通过形象的图像识别水文时间序列的各种尺度分布、变化及突变点分布.本文主要采用滑动平均法[9]、累计距平法[10]、Mann-Kendall 检验法及小波分析法等对霞曲流域的降水量进行分析.
由于霞曲流域范围内并没有站点分布,距流域最近的站点为嘉黎站,位于霞曲流域西部.该流域处于念青唐古拉山脉,其独特的地理位置使其形成了特殊的气候区.对于高原上的山区,由于地形比较复杂,降水空间差异比较大,即使相隔很短的距离,降水量与降水特征也会有很大的不同.此次分别采用本站多月降水与本站年降水相关、相邻站点相关性以及均值替代法3 种算法对降水资料进行了插补延长.根据全国降水等值线图的基础数据对霞曲流域进行了站点加密,加密站点分布如图1 所示.
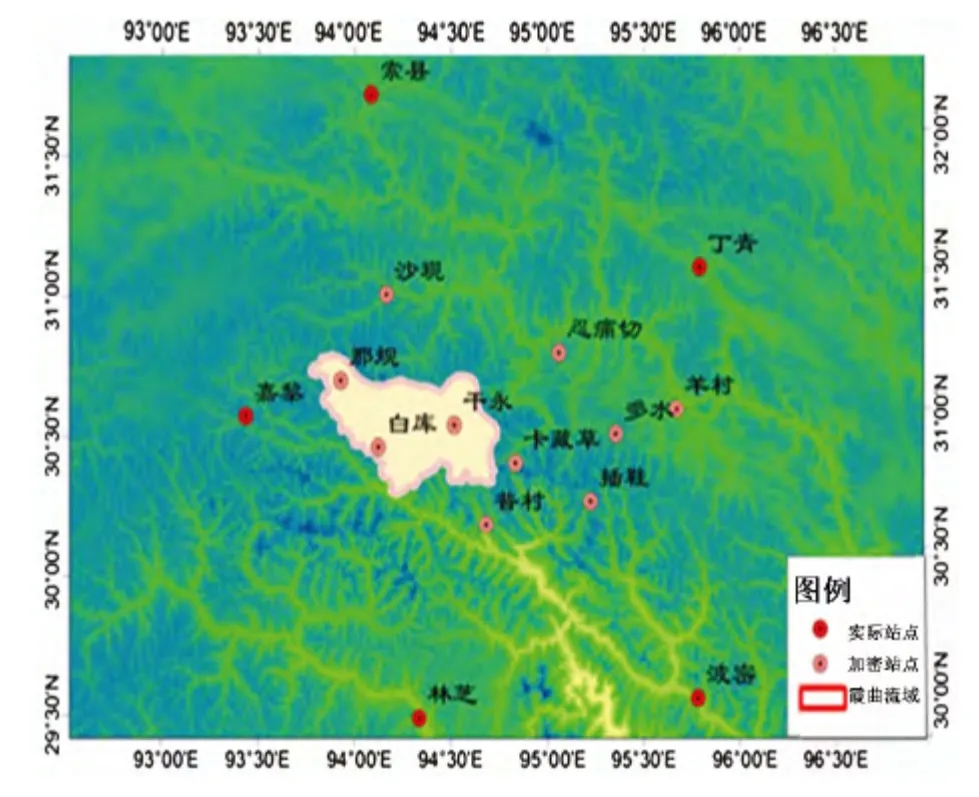
图1 霞曲流域插补站点分布图
2 结果与分析
2.1 年降水量变化分析
根据霞曲流域1956—2010 年的降水资料,采用线性倾向法和滑动平均法分析降水量变化趋势,其中显著性水平分析应用Mann -Kendall 趋势分析法,结果如图2 所示. 由图可知:最大年降水量为2 090.1 mm(2003 年),最小年降水量为1 155.8 mm(1968 年),最大值是最小值的1.8 倍;年降水量变差系数为0.13,各年降水量之间差别不大;55 a 的降水量线性倾向率为2.998 8 mm/a,55 a 降水量增加了161.9 mm,但增加不显著;Mann -Kendall 趋势检验值Z=1.66,且R2=0.055 3,没有通过95%的显著性检验.这表明,霞曲流域年降水量具有增加趋势,但不显著.
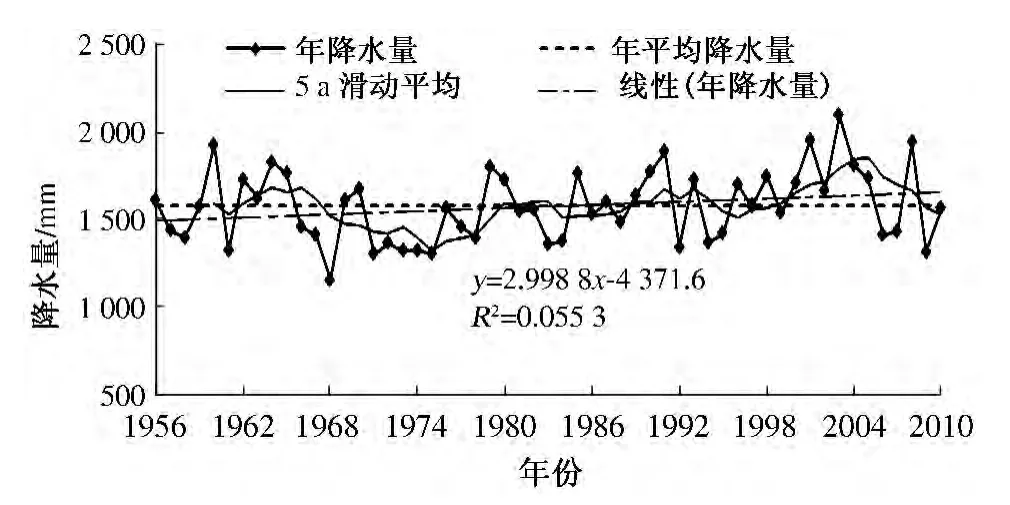
图2 霞曲流域年降水量及线性变化趋势
为了分析霞曲流域降水阶段性变化特征,采用累积距平法进行分析,结果如图3 所示. 由图可知:1956—1959 年,曲线呈下降趋势,霞曲流域少雨占优势;1960—1965 年,曲线呈上升阶段,霞曲流域处于多雨期;1965—1988 年,曲线呈波动式下降趋势,霞曲流域以少雨占优势;1989—2008 年曲线呈波动式上升趋势,霞曲流域处于多雨期. 由此可知,霞曲流域在1956—2010 年期间大致经历了少雨—多雨—少雨—多雨的4 个阶段.
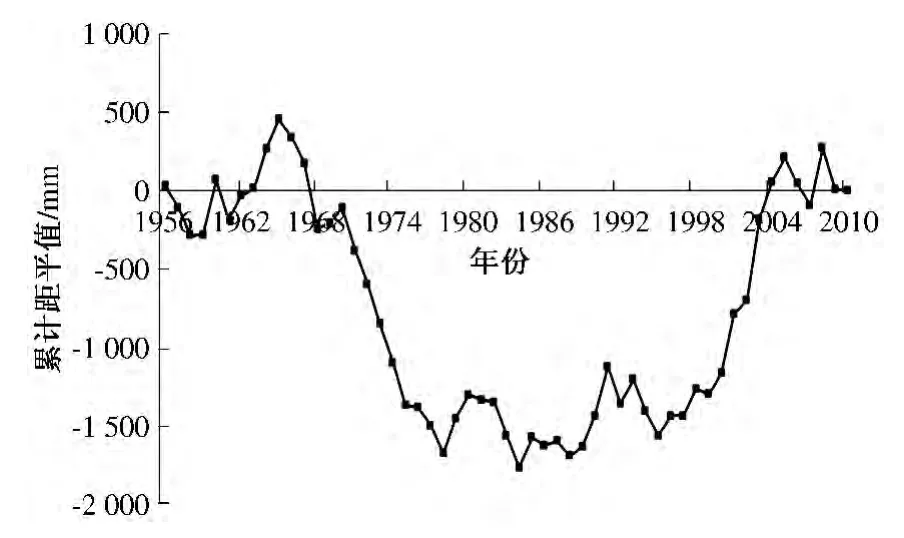
图3 霞曲流域年降水变化情况
采用Mann-Kendall 突变检验法对年降水进行突变性分析,结果如图4 所示. 由图可知:1967—1989 年UF 曲线小于0,说明年降水量在该段时间内处于下降趋势;1990—2010 年UF 曲线大于0,表明年降水量在该段时间内处于上升的趋势. UF 和UB 曲线在临界线(Uα=0.05= ±1.96)内存在交点,但交点不唯一,因此只能判断在1989 年附近降水量发生突变,再结合距平法可以判定1989 年为降水量增加的突变点.

图4 1956—2010 年平均降水量Mann-Kendall 检验
2.2 年降水量周期性分析
采用Morlet 小波对霞曲流域年降水量进行周期性分析,结果如图5—7 所示.通过小波方差确定序列的主周期,揭示不同时间尺度丰枯变化情况.小波方差可以表示降水时间序列波动能量跟随尺度的变化情况,根据小波方差公式计算年降水时间序列的各时间尺度对应的小波方差,由此可确定该流域降水时间序列的主周期.小波系数实部等值线图可以反映不同时间尺度降水量的周期性变化及其在时间域的分布.
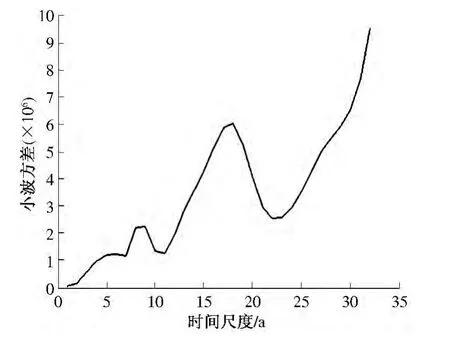
图5 霞曲流域年降水小波方差
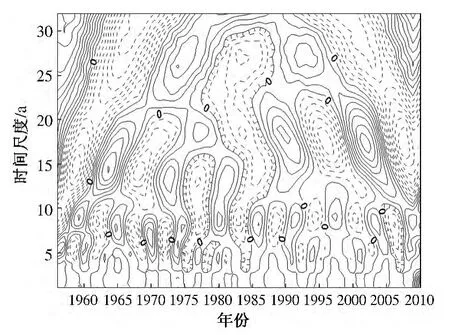
图6 霞曲流域年降水小波等值线图
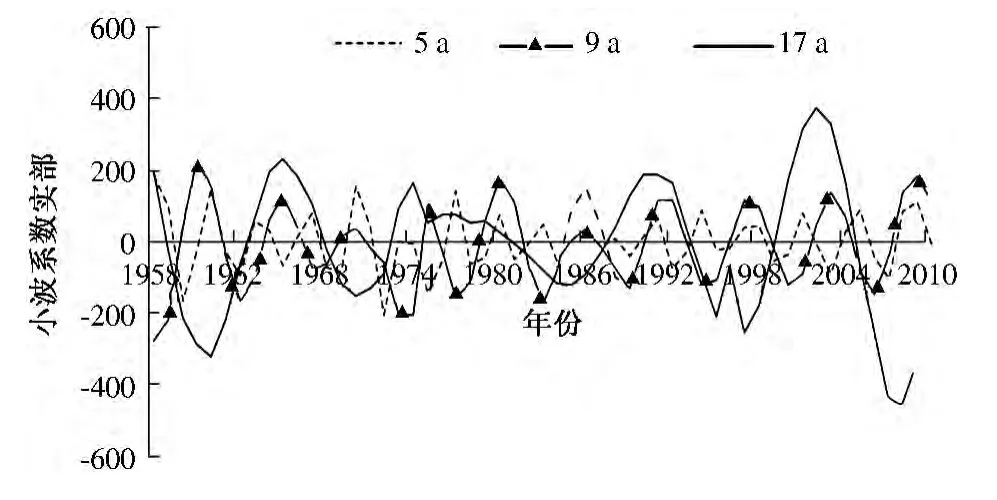
图7 霞曲流域不同时间尺度下年降水小波系数
从图5 中可以看出,存在3 个比较明显的峰值,取值分别为17、9、5 a.其中,17 a 左右的周期振荡最强,为霞曲流域年降水的第1 主周期;9、5 a 分别对应第2 主周期、第3 主周期.
从图6 和图7 中可知,降水量存在明显的年际变化.随着时间尺度的增大(从1 a 到32 a),不同尺度振荡的小波变换部分被分离开来.观察发现,降水量存在17 ~25、13 ~17、9 ~17 a 及5 a 以下4 种尺度的周期变化.在17 ~25 a 尺度降水周期振荡比较显著,出现丰、枯交替的4 次振荡.正负相位以17 ~25 a 左右的时间振荡为例,在1963—1966 年,1973—1989 年、1987—1994 年、2001—2006 年等各时段为正相位,表示降水量偏多;而在1956—1962年,1967—1972 年、1980—1986 年、1995—2000 年等各时段为负相位,表示降水量偏少.其他尺度也伴随相对多雨期和少雨期的循环交替过程.
3 结 语
1)通过线性倾向估计法、5 a 滑动平均法、累积距平法和Mann -Kendall 检验法等对霞曲流域的降水量进行分析.结果表明:霞曲流域降水量整体上呈现增长的趋势,线性倾向率为2.998 8 mm/a,但是趋势性表现得不显著;年降水量增加的突变年份为1989年;年降水量在整个研究时域内经历了丰枯交替4 个阶段,年降水量具有17、9、5 a 的主周期变化.
2)霞曲流域气象站点覆盖力度有待加强,需加强站点监控,以便更好地监测流域的气候变化,为流域水资源规划提供丰富的高原气象水文资料.
[1]雷廷,张兆吉,费宇红,等.海河平原1956—2011 年降水特征分析[J]. 南水北调与水利科技,2014,12(1):32 -36,41.
[2]张爱军,韩刚,范荣亮. 沂沭泗流域降水变化特征分析[J].水电能源科学,2012,30(7):34 -36.
[3]桑燕芳,王栋.水文时间序列周期识别的新思路与两种新方法[J].水科学进展,2008,19(3):412 -417.
[4]徐东霞,章光新,尹雄锐.近50 年嫩江流域径流变化及影响因素分析[J].水科学进展,2009,20(3):416-421.
[5]吴迪,赵勇,裴源生,等.澜沧江—湄公河流域温度和降水变化趋势分析[J]. 中国水利水电科学研究院学报,2011,9(4):304 -312.
[6]章诞武,丛振涛,倪广恒.基于中国气象资料的趋势检验方法对比分析[J].水科学进展,2013,24(4):490-496.
[7]王文圣,丁晶,向红莲. 小波分析在水文学中的应用研究及展望[J].水科学进展,2002,13(4):515 -520.
[8]桑燕芳,王栋. 水文序列小波分析中小波函数选择方法[J].水利学报,2008,39(3):295 -300,306.
[9]张仙娥,刘妞,仇亚琴,等.沂沭泗流域年降水和年地表水资源量演变趋势[J].南水北调与水利科技,2015,13(1):24 -28.
[10]杨春艳,沈渭寿,林乃峰.西藏高原近50 年气温和降水时空变化特征研究[J]. 干旱区资源与环境,2013,27(12):167 -172.
[11]张莉,屈吉鸿,陈南祥.张家港市年径流量变化及其对气候变化的响应分析[J].华北水利水电大学学报(自然科学版),2015,36(1):1 -5.

