移动测量平台在线对准方法研究
张亚男,张 震,赵桂玲,朱 红
(辽宁工程技术大学测绘与地理科学学院,辽宁阜新123000)
一、引 言
移动测量平台在工作过程中使用惯性导航系统进行初始对准,初始对准的好坏直接影响惯性导航系统的导航精度,进而影响平台的作业质量[1-2]。受作业环境的影响和自身机动的限制,移动测量平台惯性导航系统在线对准时水平失准角能满足小角度的要求,但方位失准角一般都比较大[3-4]。因此,研究大方位失准角初始对准方法是实现移动测量平台在线对准的关键。惯性导航系统初始对准一般采用单一的滤波算法对系统状态进行估计,即当系统方程为线性时,采用Kalman滤波方法进行估计[5-6],当系统方程含有非线性状态时,采用EKF、UKF、CKF、ICDKF等非线性滤波方法进行估计[7-9]。Kalman滤波能给出线性高斯模型的最优解,非线性滤波方法也能给出非线性或非高斯模型的高精度状态估计,这说明单一滤波算法在系统状态为同一性质时,能给出比较满意的估计结果。但移动测量平台在线对准系统方程既含有线性状态(水平失准角),又含有非线性状态(方位失准角),单一滤波算法并不能给出最理想的估计,其估计结果还能进一步提高[10-11]。
针对移动测量平台用惯性导航系统大方位失准角对准的特点,采用EKE-KF混合动态滤波算法进行移动测量平台在线对准来提高系统的对准精度和速度。将系统方程中的线性状态和非线性状态分离,采用EKF对系统的方位失准角进行估计,采用KF对系统的水平失准角进行估计,并利用方位失准角的估计方差对水平失准角进行修正。
二、移动测量平台在线对准误差模型
1.惯导系统在线对准误差方程
移动测量平台垂直通道的影响一般比较小,且垂直通道与水平通道的耦合很小,忽略垂直通道的影响。移动测量在线对准选取的状态变量如下
式中,δvE、δvN分别为东向和北向速度误差;φx、φy为移动测量平台在线对准水平失准角,满足小角度要求,φ为移动测量平台方位失准角,为大角度;z为水平加速度计零偏和为陀螺漂移。
移动测量平台在线对准滤波模型的状态方程为[12]
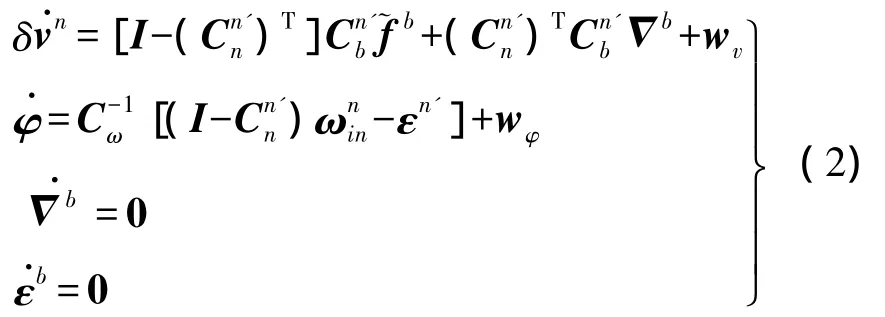
式中,˜fb为加速度输出为载体坐标系到计算导航坐标系转换矩阵为移动测量平台角速率;wv和wφ为零均值系统白噪声,并且满足E(wwT)=Q;为导航坐标系到计算导航坐标系转换矩阵。
2.EKF-KF滤波模型
EKF-KF滤波主要针对同时含有线性状态和非线性状态的系统方程,通过将状态方程中的非线性状态x1和线性状态x2分离,同时将状态方程分离为线性状态方程和非线性状态方程分别进行滤波的递推估计算法。EKF-KF滤波状态空间模型为[13]
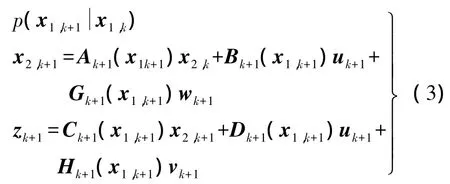
式(3)为条件线性高斯状态空间模型,是在观测条件 z1,k+1(z1,k+1= z1..zk+1{ })下,估计非线性状态x1,k+1和线性状态 x2,k+1的后验概率分布。其中,x1,k+1为一个马尔可夫过程的非线性状态;w、v为零均值高斯噪声;uk+1为控制信号;Ak+1(x1k+1)、Bk+1(x1k+1)、Ck+1(x1k+1)、Dk+1(x1k+1)、Gk+1(x1k+1)、Hk+1(x1k+1)为关于 x1,k+1的矩阵。当给定 x1,k+1后,x2,k+1满足一个线性状态空间模型。
将移动测量平台在线对准误差方程变形化简为EKF-KF滤波形式
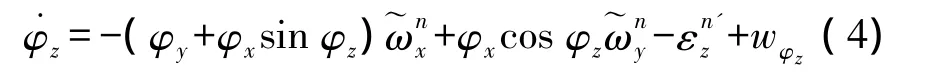

则


令系统的状态噪声w和量测噪声v为
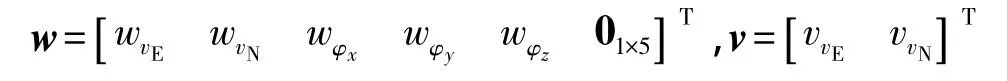
则

对系统方程和观测方程进行离散化处理,可得到移动测量平台在线对准EKF-KF滤波中的x1,k+1、x2,k+1、uk+1、wk+1、zk+1、vk+1、Ak+1(x1,k+1)、Bk+1(x1,k+1)、Ck+1(x1,k+1)、Dk+1(x1,k+1)、Hk+1(x1,k+1)、Gk+1(x1,k+1)等状态向量和矩阵。
三、移动测量平台在线对准
1.EKF估计大方位失准角
将式(4)—式(6)中的大方位失准角非线性状态方程写成如下形式

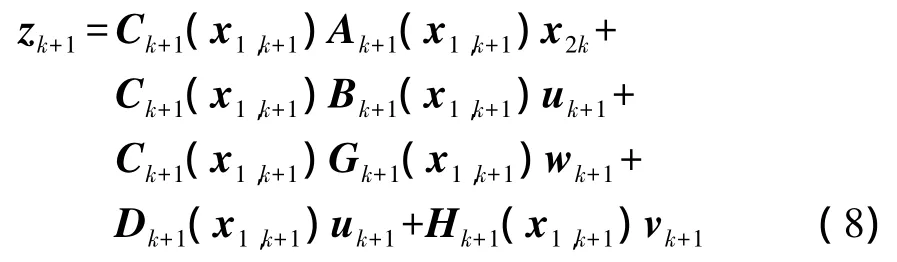
式(8)只含有非线性状态x1,k+1的观测。联立式(7)和式(8),进行EKF滤波,令

且
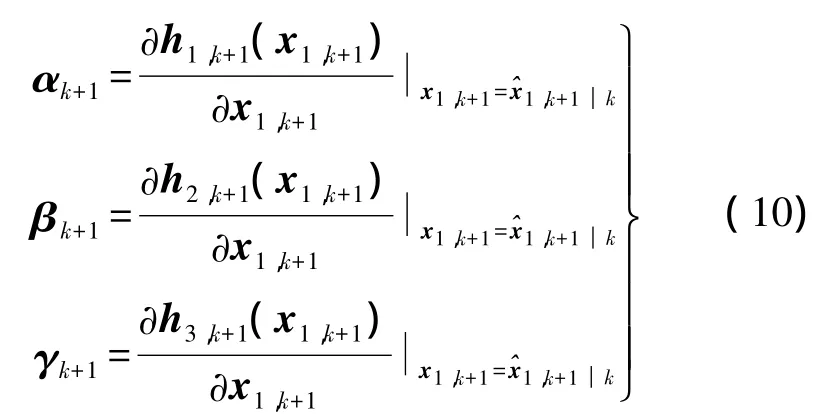
根据式(9)和式(10),可得
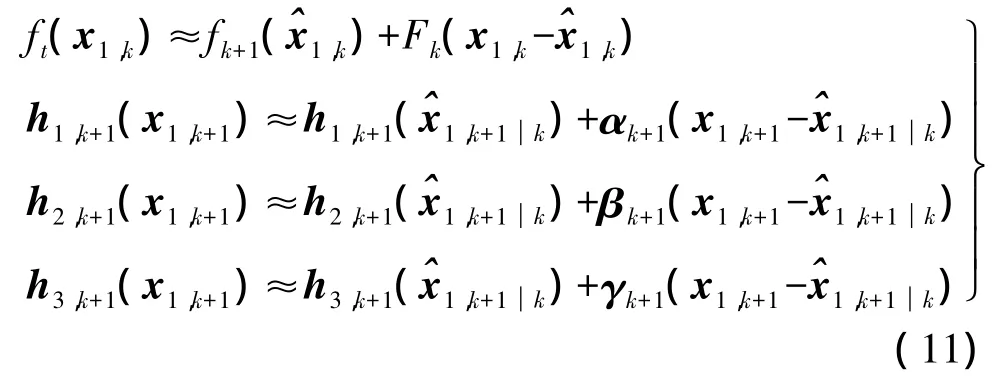
将非线性状态方程(4)和观测方程(6)线性化得
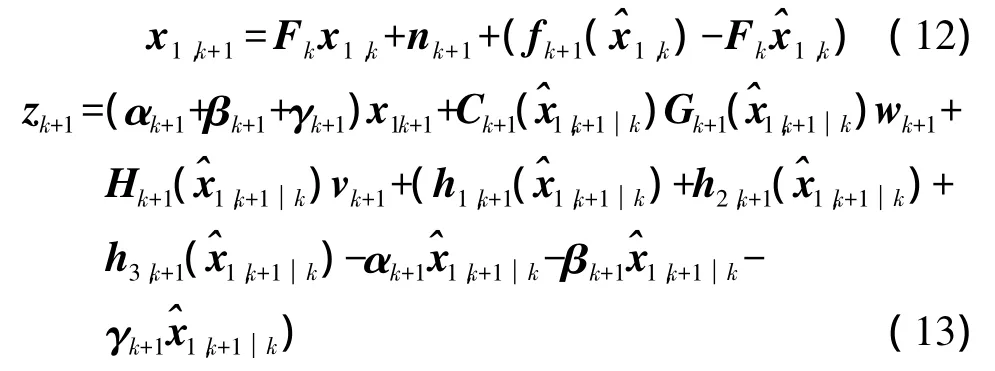
式(11)中,噪声项中的 x1,k+1用其预测值代替,令
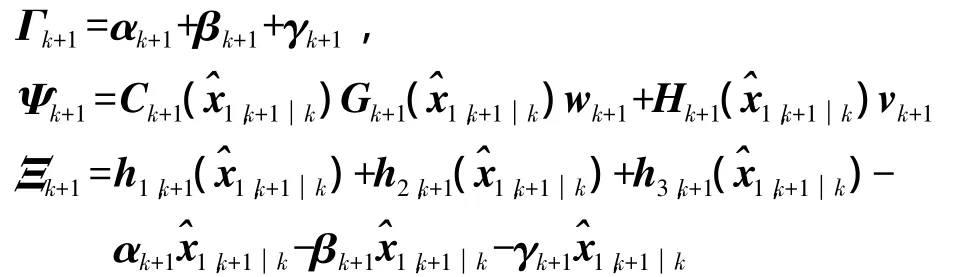
将其代入式(13)得
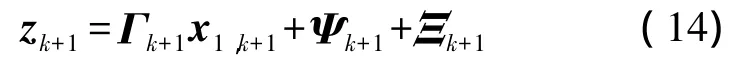
式中,Ψk+1为噪声。由于w、v为零均值的高斯噪声,Ψk+1也为零均值高斯噪声,w、v的方差分别为Q和R,设 Ψk+1的方差为 Λk+1,可得

根据EKF滤波基本方程可得

其中

Jk表示线性状态 x2在 k时刻的估计方差。将式(16)与EKF基本方程比较,可以看出Gk+1的求取中多了Ck+1Ak+1Jk(Ck+1Ak+1)T)这一项,这是因为在估计时用到了 x2,k的估计,而 ^存在估计方差 Kk。
2.KF估计线性状态
前面讨论了非线性状态x1,k+1的估计,在获得了非线 性 状 态 x1,k+1的 估 计后,将代 入式(3)得

并令
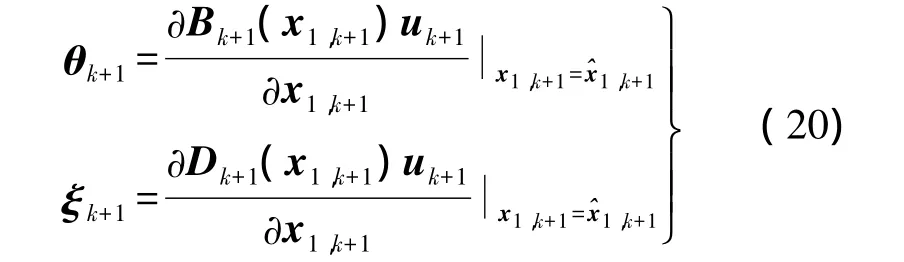
由KF基本方程可得
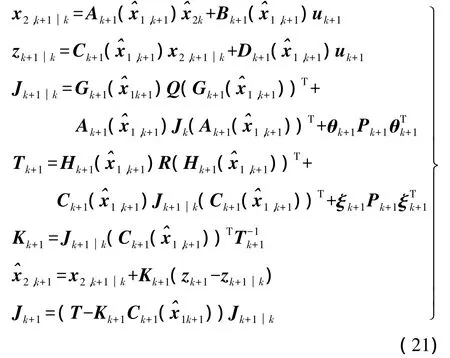
式中,Kk+1为Kalman滤波增益;Jk+1为Kalman滤波方差为Kalman滤波预测方差。与普通的Kalman滤波相比,式(21)中和Tk+1的两项最后分别加上了,这是因为在估计线性状态 x2,k+1时用到了非线性状态 x1,k+1的估计,而非线性状态存在估计方差 Pk+1。的加入能有效提高移动测量平台在线对准的精度。
四、仿真结果及分析
本文对基于EKF-KF的移动测量平台在线对准方案进行仿真验证,仿真采用的惯性导航系统陀螺常值漂移 0.01°/h,随机漂移 0.001°/h;加速度计常值零偏 10-4g0,随机零偏 10-5g0;初始失准角0.5°、0.5°、15°。得到的仿真结果如图1—图3、表1所示。
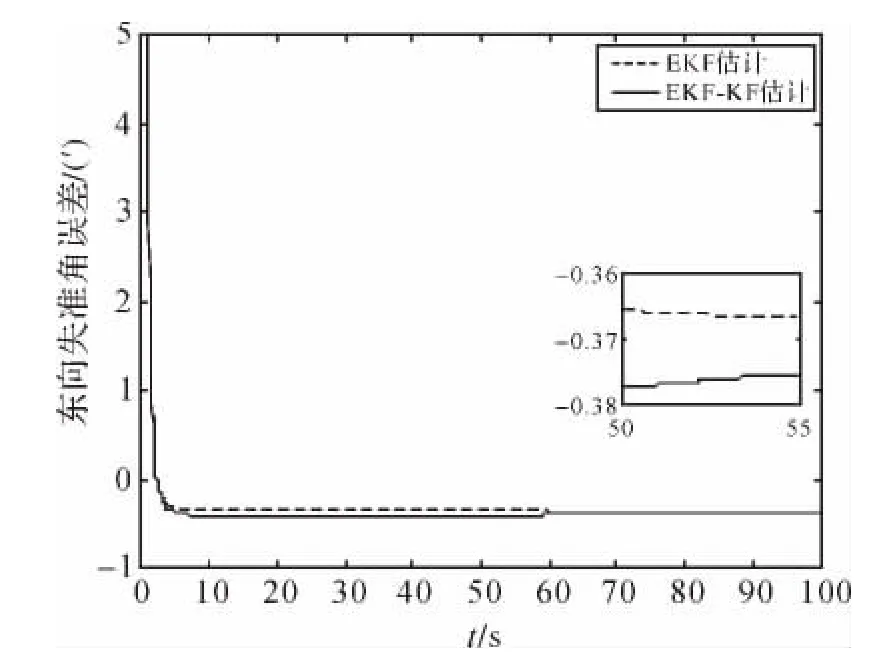
图1 东向失准角估计误差

图2 北向失准角估计误差
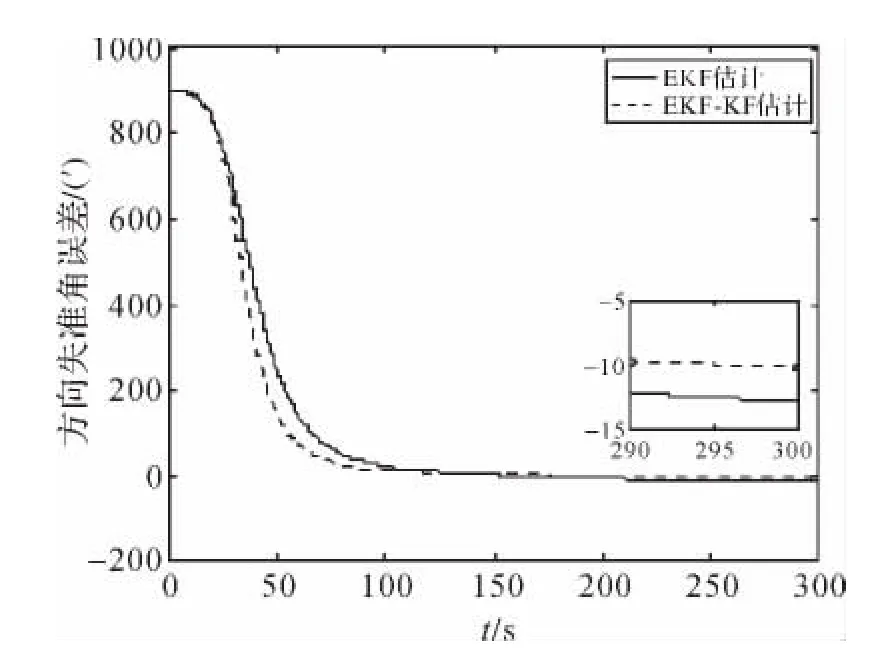
图3 方位失准角估计误差

表1 失准角估计误差比较 (')
由表1可以看出,移动测量平台采用EKF-KF进行在线对准的失准角估计误差小于采用EKF进行失准角估计的误差。这主要是因为在估计水平失准角时用到了方位失准角的估计方差Pk+1,θk+1Pk+1·的加入有效提高了滤波精度。
五、结束语
本文针对移动测量平台在线对准的大方位失准角问题,将混合动态滤波方法EKF-KF用于失准角误差估计,采用EKF估计移动测量平台的大方位失准角,采用Kalman滤波估计移动测量平台的水平失准角,并将方位失准角的估计误差对水平失准角估计进行修正。与采用单一的非线性滤波方法EKF的对准结果进行比较:EKF-KF滤波精度高于EKF滤波精度,尤其是方位失准角的估计精度大幅度提高。按照EKF-KF滤波算法的思路,同样可以将UKF-KF、CDF-KF、GHF-KF等混合滤波算法应用于移动测量平台大方位失准角在线对准中。
[1]麦照秋,陈雨,郑祎,等.IP-S2移动测量系统在高速公路测量中的应用[J].测绘通报,2010(12):23-26.
[2]宫晓琳,房建成.一种机载遥感成像用分布式POS传递对准方法[J].北京航空航天大学学报,2012,38(4):491-496.
[3]BARBOUR N.Inertial Navigation Sensors[R].Cambridge:Charles Stark Draper Laboratory,2011.
[4]陈雨,赵剡,李群生.基于惯性参考系线性滤波传递对准方法[J].系统工程与电子技术2013,35(12):2577-2581.
[5]杨晓霞,阴玉梅.可观测度的探讨及其在捷联惯导系统可观测性分析中的应用[J].中国惯性系技术学报,2012,20(4):405-409.
[6]BANCROFT J B,LACHAPELLE G.Data Fusion Algorithms for Multiple Inertial Measurement Units[J].Sensors,2011,11(7):6771-6798.
[7]熊剑,魏林生,郭杭,等.方位大失准角的捷联惯导非线性快速对准研究[J].测绘通报,2013(8):6-9.
[8]郝燕玲,牟宏伟,贾鹤鸣.ICDKF在SINS大方位失准角初始对准中的应用[J].系统工程与电子技术,2013,35(1):152-155.
[9]郭泽,缪玲娟,赵洪松.一种改进的强跟踪UKF算法及其在SINS大方位失准角初始对准中的应用[J].航空学报,2014,35(1):203-214.
[10]尹建君.线性/非线性系统的混合动态滤波算法理论及应用[D].上海:复旦大学,2008.
[11]DMITRIYEV S P,STEPANOV O A,SHEPEL S V.Nonlinear Filtering Methods Applications in INS Alignment[J].IEEE Transaction on AES,1997,33(1):268-276.
[12]柴华,王勇,许大欣,等.地固系下四元数和卡尔曼滤波方法的惯导初始精对准研究[J].武汉大学学报:信息科学版,2012,37(1):68-72.
[13]赵桂玲.船用光纤捷联惯导系统标定与海上对准技术研究[D].哈尔滨:哈尔滨工程大学,2011.

