浙江省用水结构的组合预测*
胡玉琴、薛留根
(1浙江财经大学数学与统计学院/2北京工业大学应用数理学院,浙江杭州 310018/北京 100000)
浙江省用水结构的组合预测*
胡玉琴1、薛留根2
(1浙江财经大学数学与统计学院/2北京工业大学应用数理学院,浙江杭州 310018/北京 100000)
本文以浙江省用水结构为研究对象,在分别应用对数比变换和球面投影变换与灰色预测模型GM(1,1)结合的成分数据单一预测方法的基础上,提出成分数据Aitchison距离最小化方法确定组合权重的组合预测方法,并对浙江省2013-2017年的用水结构进行预测。研究表明,组合预测能较好地提高预测的精度,增强预测的稳定性。
用水结构;成分数据;组合预测
一、引言
水资源作为人类赖以生存的自然资源,是国民经济和社会发展的重要保障。随着城市化进程的不断推进,区域经济增长需求与日益紧缺的水资源的矛盾凸显。这一问题在经济发达但人均水资源并不丰富的浙江省应该引起关注。用水结构作为水资源在区域生产生活各部门的分配结果,其结构特征直接反映水资源的可持续性发展状况。因而研究浙江省的用水结构状况并预测其发展趋势,对于合理安排浙江省用水结构,实现水资源的合理配置,促进经济发展有着重要的意义。
用水结构主要根据经济活动进行分类,由农业用水、工业用水和生活用水组成。随着人们对环境保护意识的提高,增加新的统计分类——生态用水。根据《中国统计年鉴》,浙江省自2003年开始对生态用水进行统计,用水结构由农业用水、工业用水、生活用水以及生态用水这四部分组成,具体数据见表1。2003-2012年浙江省的总用水量呈现出先升后降,之后逐渐趋于平稳的过程。总用水量从2003年的205.98亿立方米上升到2008年的216.62亿立方米,随后下降到2009年的197.76亿立方米,之后趋于平稳,在200亿立方米左右。农业用水是浙江省用水比重最大的部分,但其比重总体呈现下降趋势,由2003年的53.5%下降到2008的45.6%,2009年上升到49.2%,2010年开始缓慢下降至2012年的46.1%;工业用水比重是浙江省用水的第二大用水部分,总体变动比较平缓,从2003年的26.8%上升2007年的30.4%,2008-2012年在30%左右波动;生活用水比重呈现明显的上升趋势,由2003年的14.1%上升至2012年的21%;生态用水比重在2003-2007年间在6%左右浮动,2008年达到最高值9.5%,之后下降达到2012年的2.3%。
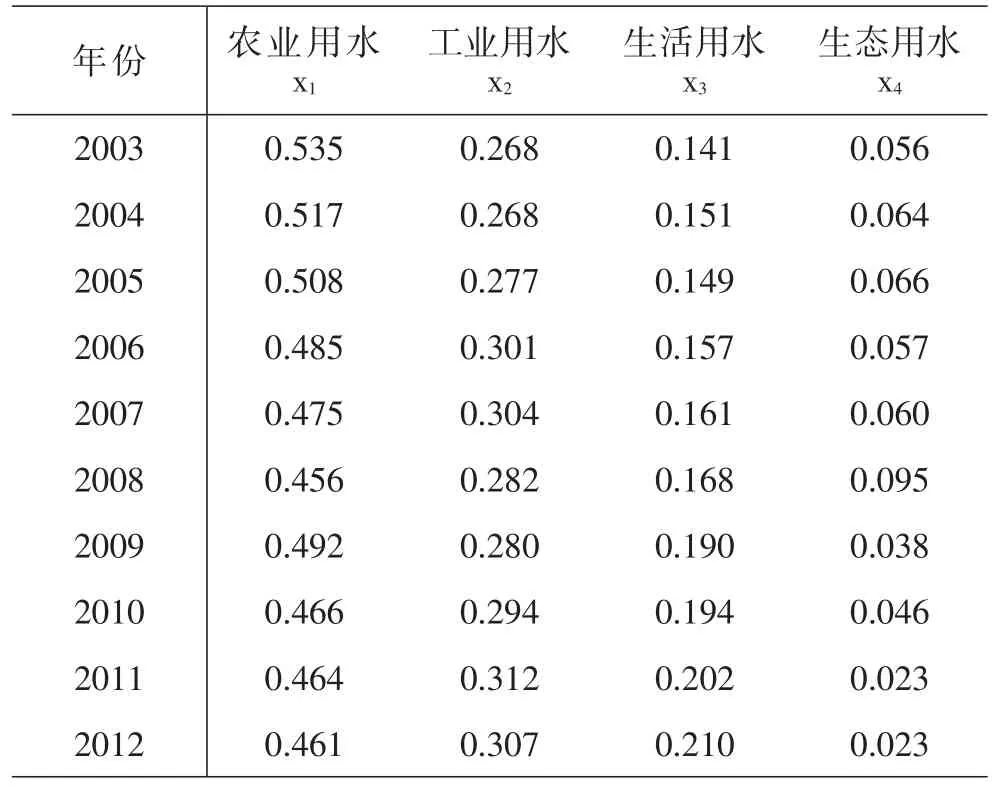
表1 浙江省2003-2012年用水结构
从数据结构来看,用水结构为成分数据(compositional data),可用描述统计学中的饼图来表示某一事物中各种成分所占的比重。用数学形式表达,p维成分数据x=(x1,x2,…,xp),其中xi>0,i=1,2,…,p,满足x1+x2+…+xp=1。由于成分数据始终存在定和条件1的约束,单一对各成分进行预测会使得预测结果不满足定和条件1,因而在研究中应对成分数据进行整体分析,运用成分数据统计方法进行研究[1-2]。
本文以浙江省的用水结构为研究对象,分别运用成分数据的对数比变换和球面坐标变换分析并预测用水结构,并提出组合预测方法提高用水结构预测的精度。
二、成分数据的单一预测
定和约束的存在使得成分数据各分量间存在完全多重相关性,对原始成分数据采取数据变换,突破定和条件约束,然后采用常规统计方法对变换后的数据进行预测,从而利用反变换公式预测原始成分数据是解决成分数据预测的主要思路。目前主要有对数比变换和球面投影坐标变换进行成分数据的单一预测。
(一)基于对数比变换的成分数据预测
对成分数据x=(x1,x2,…,xp)作对数比变换:
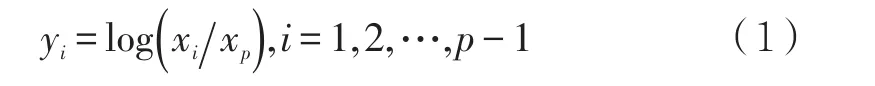
将p个线性相关的变量xi,i=1,2,…,p转换成p-1个独立并在(-∞,+∞)内取值yi,i=1,2,…,p-1。
利用常规统计方法对yi,i=1,2,…,p-1进行分析,然后根据反变换公式
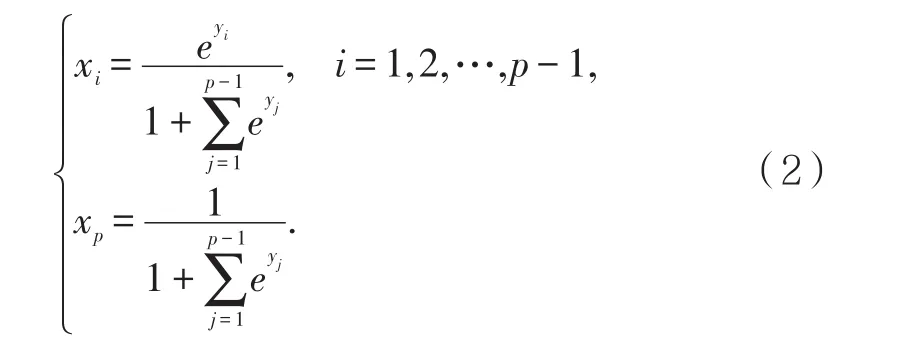
得到对应xi,i=1,2,…,p的相应预测值,用表示。
(二)基于球面投影变换的成分数据预测
对成分数据x=(x1,x2,…,xp)首先作变换,此时z=(z1,z2,…,zp)分布在半径为1的p维超球面上;然后将z=(z1,z2,…,zp)
从直角坐标系变换到球面坐标系中,得到z=(1,θ2,…,θp,即
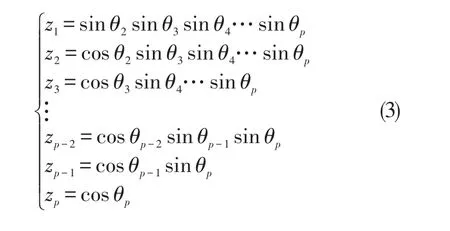
从而将p个线性相关变量转换成p-1个独立的转角θi,i=2,3,…,p。
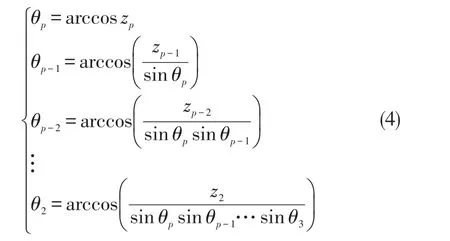
利用常规统计方法对θi,i=2,3,…,p进行分析然后根据反变换公式(4)式得到zi,i=1,2,…,p的预测值,从而根据xi=(zi)2得到xi,i=1,2,…,p的预测值,用表示。
(三)浙江省用水结构的单一预测
对表1中的数据进行对数比变换得到y1,y2,y和进行球面投影变换θ2,θ3,θ4,汇总见表2。根据散点图,2008年作为异常值进行处理,因而剔除2008年数据。由于采取9年的数据,数据点较少采用灰色预测模型GM(1,1)分别对y1,y2,y3,θ2,θ3,θ进行预测。由表3,各个GM(1,1)模型的后验差检验比C均小于0.35,表明预测精度等级均为好,模型具有较好的拟合效果和预测精度。
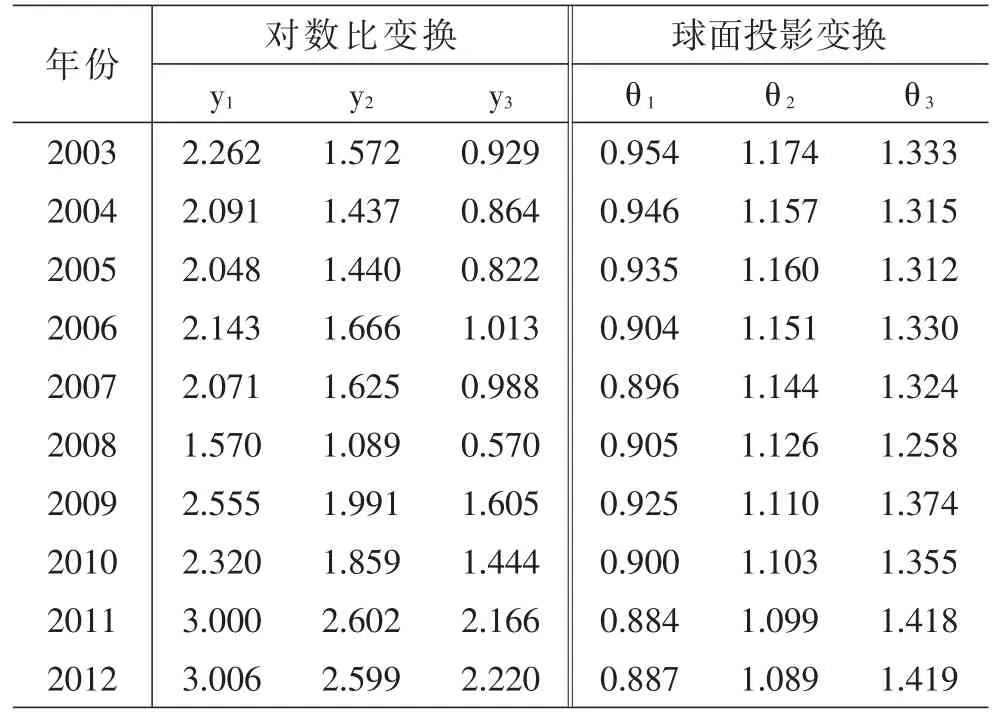
表2 对数比变换和球面投影变换数据表

表3 各个GM(1,1)模型的预测检验精度
根据各个GM(1,1)模型可得到2003-2012年(2008年除外)的拟合值BZ_8_525_553_558_589.png1,BZ_8_525_553_558_589.png2,BZ_8_525_553_558_589.png3,BZ_67_2031_2530_2056_2665.png2,BZ_67_2031_2530_2056_2665.png3,BZ_67_2031_2530_2056_2665.png4,根据相应反变换公式可得到2003-2012年(2008年除外)浙江省用水结构单一拟合值。表4中分别表示基于对数比变换与GM(1,1)方法下农业用水、工业用水、生活用水以及生态用水的拟合值。分别表示基于球面投影变换与GM(1,1)方法下农业用水、工业用水、生活用水以及生态用水的拟合值。由图1可以看出基于对数比变换和球面投影变换的用水结构拟合值与真实值的拟合效果理想。
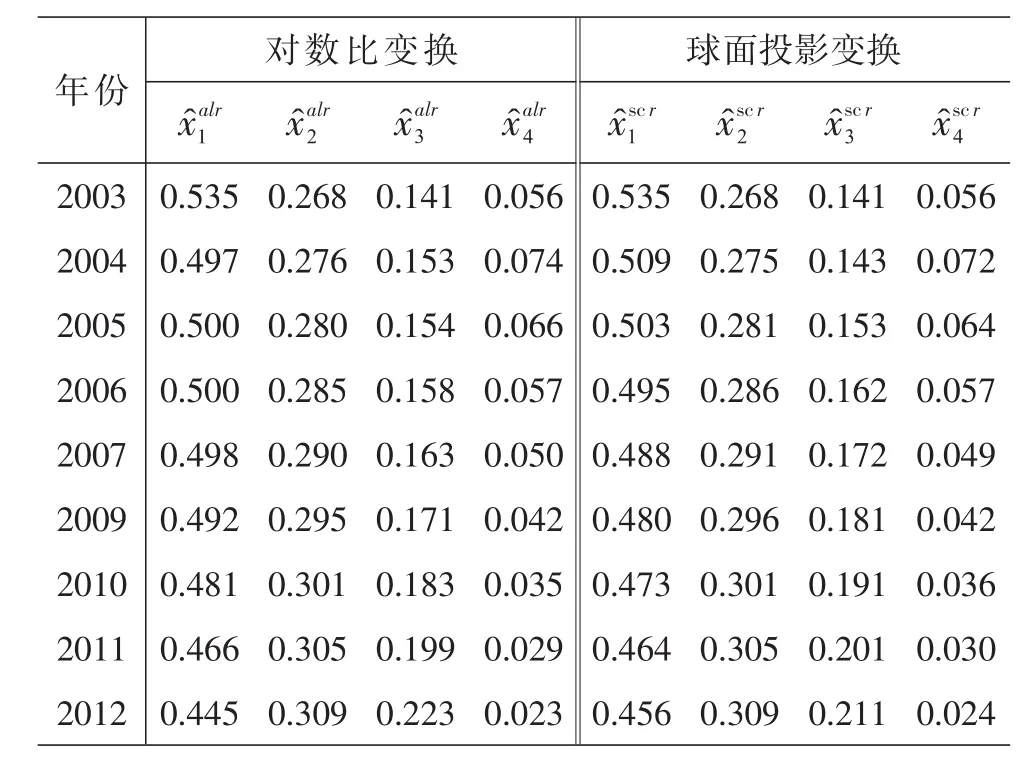
表4 浙江省用水结构的对数比变换和球面投影变换拟合值
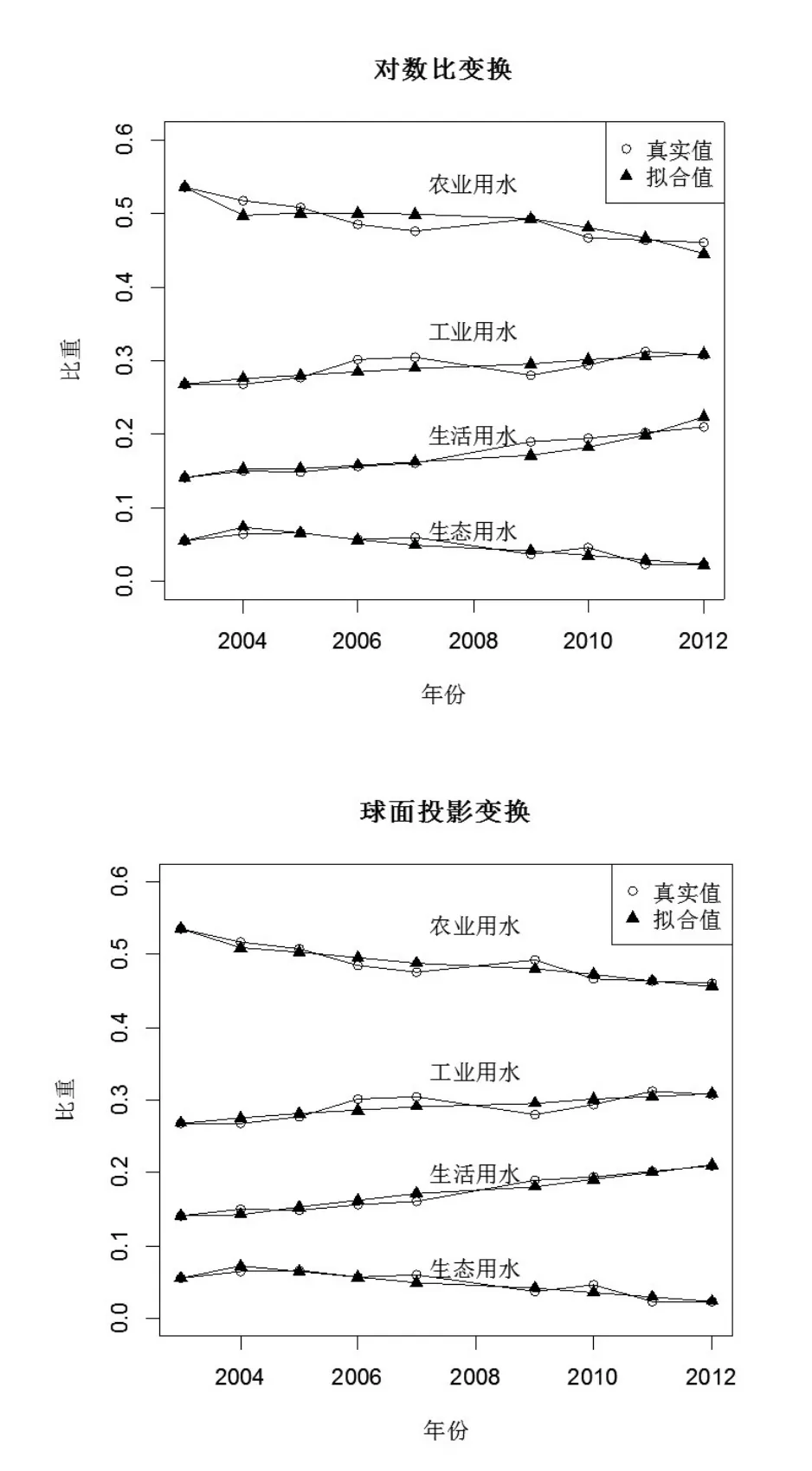
图1 对数比变换和球面投影变换的浙江省用水结构拟合图
由于GM(1,1)适用于中短期预测,根据各个GM(1,1)模型得到2013-2017年的预测值1,2,y3,2,3,4,由相应反变换公式可以得到对2013-2017年未来五年的浙江省用水结构的单一预测。由表5,可以看到对数比变换和球面投影变换单一预测在生态用水比重上相一致,在农业用水和生活用水的预测趋势上保持一致,但是球面投影变换变动幅度较小,对数比变换的变动幅度较大。在工业用水比重预测中,对数比变换预测趋势下降,而球面投影变换预测趋势则是上升。由于组合预测能够充分利用单预测模型的信息,就有较高的适应能力,因而采取将对数比变换和球面投影变换预测的组合预测方法。
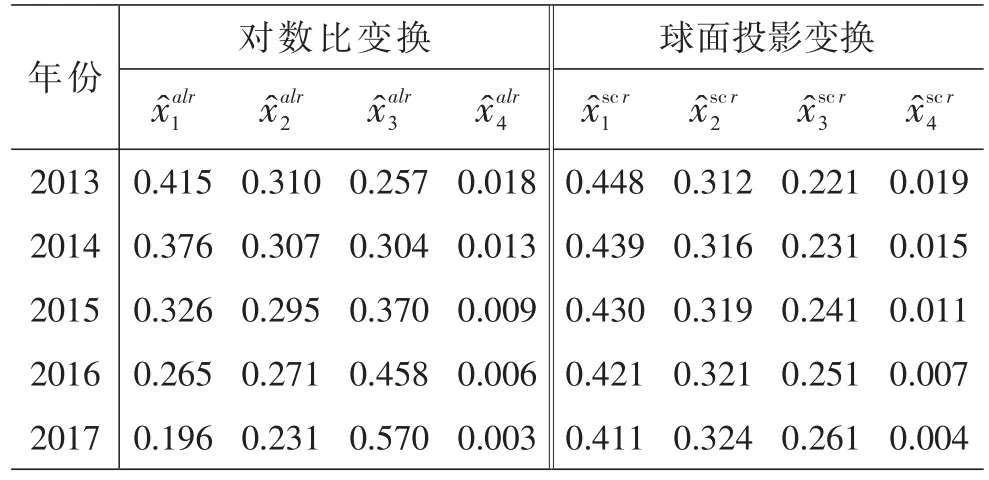
表5 浙江省用水结构2013-2017年的对数比变换和球面投影变换预测值
三、成分数据的组合预测
(一)Aitchison距离
由于受定和条件的约束,成分数据运算具有闭合性特点,因而成分数据的预测值与真实值之间的误差,不能用欧几里得空间的欧式距离度量,而应采用单形空间的Aitchison距离[7]进行度量。
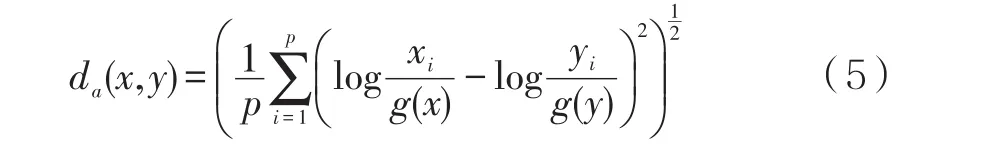
Aitchison距离小,则预测精度高,反之,则预测精度低。
根据表4,分别计算2003-2012年(2008年除外)的用水结构的对数比变换拟合值xalr和球面投影变换拟合值xscr与真实成分数据x的Aitchison距离分为da(x,xalr)和da(x,xscr)。由表6的第二列和第三列可知,由于采取灰色预测模型GM(1,1)方法进行预测估计,两种单一预测在2003年均没有预测误差,2006、2007、2009以及2011这4年的对数比变换预测精度高于球面投影变换,而2004、2005、2010以及2012这4年的球面投影变换预测精度高于对数比变换。两种单一预测方法各有优缺点。
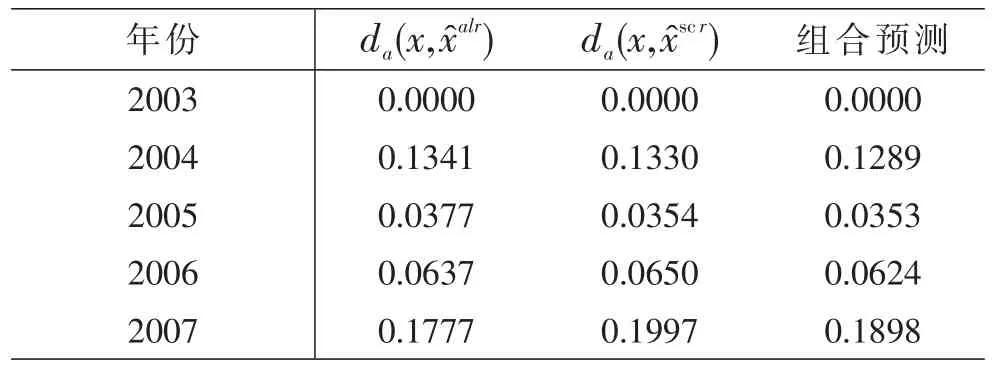
表6 对数比变换和球面投影变换的Aitchison距离
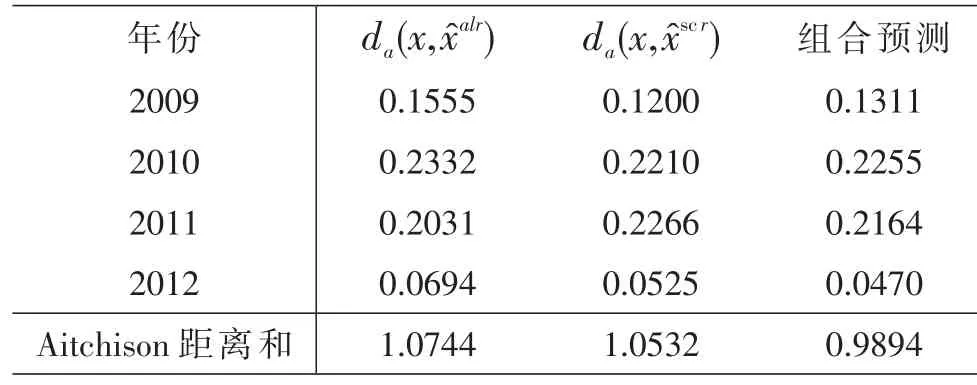
续表
(二)组合权重的确定
用对数比变换预测值xalr和球面投影变换预测值xscr的组合W1xalr+W2xscr(其中W1+W2=1,W1,W2≥0进行预测。关键是解决权重W1,W2的确定问题。
权重W1,W2应使得拟合值与真实值x的Aitchi son距离之和最小,可表示为
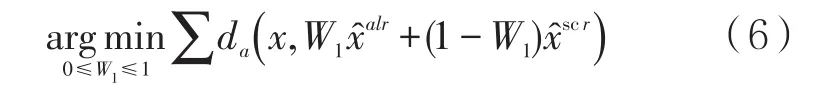
(三)浙江省用水结构的组合预测
根据表4和表5,分别对基于对数比变换和球面投影变换单一预测的拟合值和预测值用组合预测x*=0.385xalr+0.615xscr对浙江省用水结构进行分析,可得到表7。由图2,可以看出组合预测具有较好的拟合效果,其精度高于单一预测。
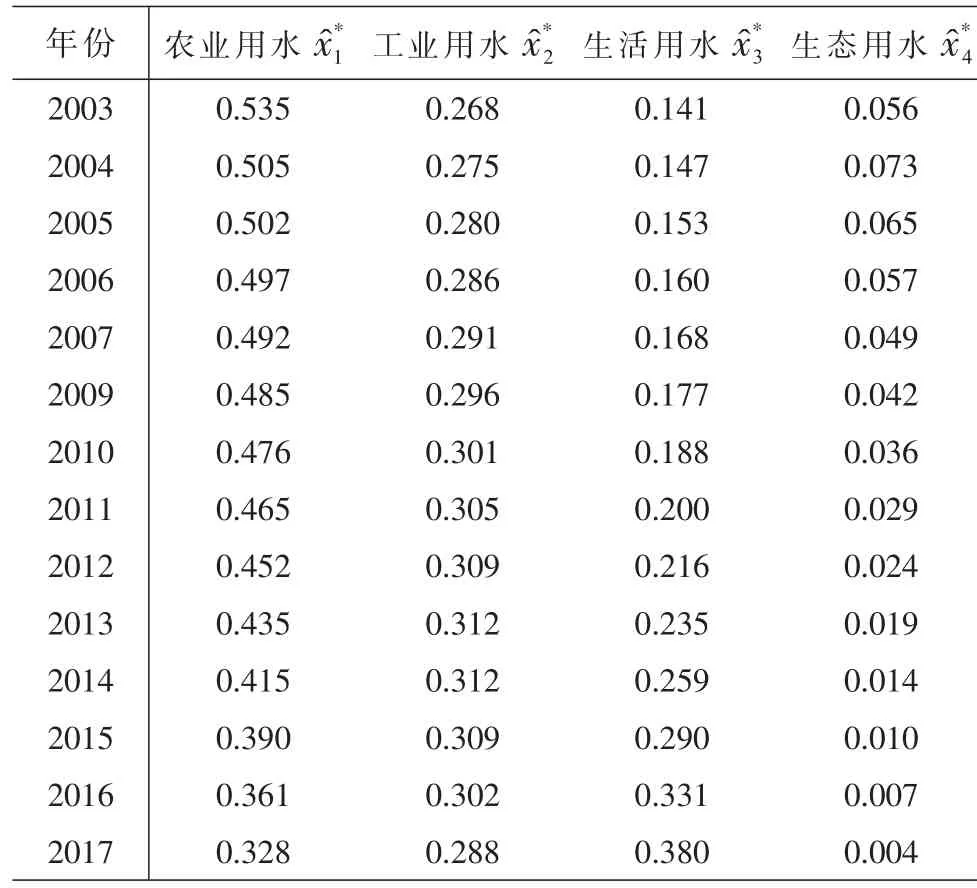
表7 浙江省用水结构的组合预测
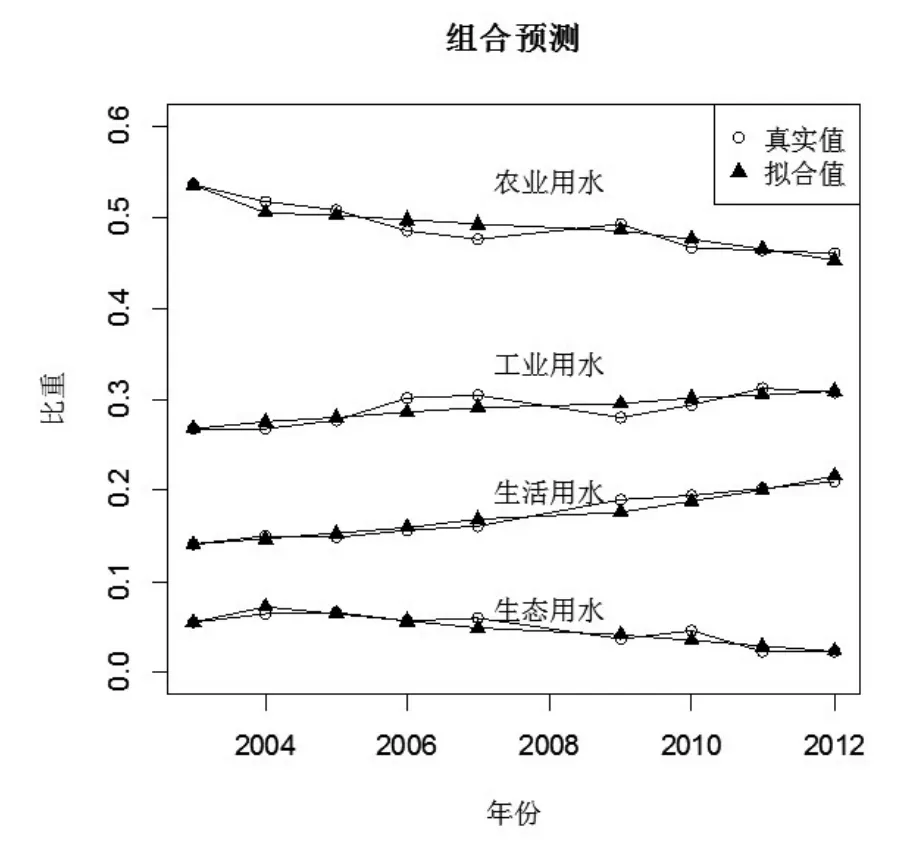
图2 浙江省用水结构组合预测拟合图

图3 2013-2017年浙江省用水结构预测
用组合预测对浙江省2013-2017年用水结构进行预测,见表7和图3,浙江省农业用水所占比重持续下降,从2013年的43.5%下降到2017年的32.8%,工业用水比重下降趋势较缓,从2013年的31.2%下降到2017年的28.8%,生态用水则从2013年的1.4%下降到2017年的0.4%,生活用水比重则呈现显著上升趋势,从2013年23.5%,上升到2017年的38%,2017年超过农业用水,成为浙江省用水比重最大的部分。
四、小结
针对用水结构这一成分数据,本文首先分别运用成分数据对数比变换和球面投影变换与灰色预测模型GM(1,1)方法对浙江省2003-2012年的用水结构进行分析,分析表明,尽管对数比变换和球面投影变换预测能够达到较好的拟合效果,但是单一预测的结果相差较大。为提高预测精度,本文运用组合预测方法,利用使得成分数据Aitchison距离最小来确定权重系数,得到较好的拟合精度和预测效果。
值得说明的是,本文用R软件进行编程和分析,成分数据的Aitchison距离计算借助compositions包[8]来进行。
[1]Aitchison J.The Statistical Analysis of Compositional Data[M].London:Chapman and Hall,1986
[2]张尧庭.成分数据统计分析引论[M].北京:科学出版社,2000.
[3]王惠文,刘强.成分数据预测模型及其在中国产业结构趋势分析中的应用[J].中外管理导报,2002(5):27-29.
[4]赵江涛,黄薇,王惠文.两种成分数据预测建模方法的比较研究[J].北京航空航天大学学报:社会科学版,2003,16(2):37-40.
[5]施久玉,柴艳有.灰色成分数据模型在中国产业结构分析预测中的应用[J].统计与信息论坛,2007,22(1): 32-35
[6]张晓琴,陈佳佳,原静.成分数据的组合预测[J].应用概率统计,2013,29(3):307-316.
[7]Aitchison J,Barceló-Vidal C,Martín-Fernández JA,Pawlowsky-Glahn V.Logratio Analysis and Compositional Distance[J].Math.Geol.2000,32(3),271-275.
[8]Gerald van den Boogaart KG,Tolosana-Delgado R. "compositions":a unified R package to analyze Compositional Data[J].Computers&Geosciences,2008,34(4),320-338.
(责任编辑:牛域宁)
*本文课题项目来源:全国统计科学研究计划项目(2013LY103)、国家社科基金青年项目(13CTJ012)、国家社科基金项目(14BTJ031)、浙江省2014年度统计研究重点课题。

