双缆多跨悬索桥力学性能及主缆用钢量研究

柴生波+王秀兰+任翔

摘要：为了进一步明确双缆多跨悬索桥的力学和经济性能，比较了双缆多跨悬索桥与传统多跨悬索桥在活载作用下的加劲梁变形及桥塔受力，分析了二者主缆用钢量的差异；拟定双缆体系与传统体系的四塔三跨悬索桥有限元模型，分别计算了活载作用下的结构变形及受力。研究结果表明：双缆悬索桥体系的主缆纵向刚度可达传统悬索桥体系的2～4倍甚至更高，双缆体系纵向刚度与上缆和下缆的垂度及恒载在上下缆之间的分配比例有关，双缆体系主缆用钢量与传统体系相当；在桥塔抗推刚度相对较低的情况下，双缆多跨悬索桥在活载作用下的加劲梁挠度及塔底弯矩均远小于传统多跨悬索桥体系，采用双缆体系可有效增大多跨悬索桥的结构刚度。

关键词：悬索桥；双缆；多跨；力学性能；用钢量

中图分类号：U448.25 文献标志码：A

0 引 言

进入21世纪，跨海桥梁不断涌现，桥梁的跨度纪录被不断刷新，现有桥梁结构的跨越能力已经接近极限，迫切需要发展新型超大跨度桥梁结构[1-2]。Gimsing[3]曾设想过一种双主缆悬索桥结构，在同一索面采用垂度不同的2根主缆，2根主缆用吊索相连，下缆通过吊索与桥面相连，或者上缆与下缆分别与桥面直接相连。然而，目前对双缆体系的研究不多，双缆体系是否适合于建造多跨悬索桥尚待进一步研究。

双缆体系在多跨悬索桥中重要的潜在应用价值引起众多学者的关注，对其力学特性已经有初步研究。陈艾荣等[4]分析了几种有可能用于多跨悬索桥的新型缆索体系，认为双缆体系具有良好的刚度特性，非常适合于建造多跨悬索桥。张新军等[5]研究了双缆体系的抗风稳定性，认为采用双缆体系的三塔悬索桥相比于传统的三塔悬索桥可以改善结构的抗风稳定性。张劲泉等[6]指出Gimsing关于均布荷载作用下双缆受力的研究结论是错误的，双缆体系在大跨度悬索桥中是否适用尚需进一步论证。柴生波等[7-9]研究了均布荷载作用下双缆的受力，推导了双缆体系对桥塔的纵向约束刚度。Gimsing等[10]对比了双缆多跨悬索桥与传统三塔悬索桥体系主缆用钢量，认为双缆体系主缆用钢量将比传统体系多约20%，桥塔材料用量减小约15%。肖汝诚[11]研究了活载作用下双缆多跨悬索桥的变形及桥塔受力，认为多跨悬索桥在刚度方面具有优势，但主缆与鞍座之间的抗滑稳定性较难满足。由此可见，目前对双缆多跨悬索桥的研究尚处于初步阶段，对其力学性能缺乏深入了解。虽然已有研究确认了双缆多跨悬索桥在结构刚度方面具有优势，但双缆体系对于增大结构刚度的效果尚缺乏定量研究。另外，采用双缆体系时，主缆用钢量是否多于传统悬索桥也无定论，这些问题决定了双缆多跨悬索桥是否可行，因此需要进一步研究。

目前，双缆体系悬索桥尚处于理论发展阶段，还未用于实际工程。一是因为双缆体系的理论发展尚不完备，双缆的合理成桥状态、施工控制等还未见相关研究报道；二是因为双缆体系的优势在于其主缆的纵向刚度大，这种优势仅在建造多跨悬索桥时才能体现出来，目前世界上建造大跨度多跨悬索桥处于起步阶段，并且仅有的几座大跨度悬索桥沿用了传统的缆索体系。

为明确双缆多跨悬索桥这种新型桥梁结构的适用性，本文首先比较双缆的纵向约束刚度与传统悬索桥主缆的纵向约束刚度，推导主缆用钢量计算公式。拟定1座具有3个主跨的多跨悬索桥，分别采用传统缆索体系与双缆体系2种形式，比较二者在活载作用下加劲梁的变形以及桥塔的受力情况，分析双缆多跨悬索桥与传统多跨悬索桥体系主缆用钢量差异。

1 主缆纵向约束一般原理

图1为双缆悬索桥示意。在多跨悬索桥中，中间桥塔在不平衡活载作用下的纵向变形是造成结构变形过大的主要原因。中塔的变形除了受其本身抗推刚度的影响，还取决于主缆对桥塔的约束作用。如图2所示的传统多跨悬索桥，若活载作用于中间主跨，则加载跨主缆内力增大，2号塔和3号塔发生朝向加载跨的位移。以2号桥塔为例，其位移大小不仅取决于桥塔本身刚度，同时取决于1号塔和2号塔之间的主缆对2号桥塔的约束作用。若桥塔之间的纵向联系足够强大，则活载作用下各个桥塔便可以协同受力，增大结构刚度，减小变形。

传统的悬索桥体系主缆纵向约束主要来自于主缆线形改变引起的水平力改变，恒载作用下主缆水平力H可由式（1）求得

H=gL28f

（1）

式中：L为跨长；f为主缆垂度；g为恒载集度。

桥塔发生纵向位移时，主缆线形发生改变，主缆水平力也发生变化，由此产生对桥塔的约束作用。

双缆悬索桥体系（图3）对桥塔的纵向约束与传统悬索桥体系差异较大。采用双缆体系的悬索桥在桥塔发生纵向位移时，由于2根主缆的垂度不同，塔顶位移引起的主缆垂度改变量也不同，2根主缆之间的距离有改变的趋势，连接上缆与下缆的吊杆内力产生变化，由此造成了荷载在2根主缆之间的重新分配。荷载在上缆与下缆之间的重新分配导致了主缆水平力的改变，由此形成了对桥塔的约束作用[8-9]。

研究结果表明，双缆的纵向约束比传统悬索桥体系更为强大。双缆悬索桥中间主跨受到活载作用时，双缆体系能够将活载引起的主缆水平力增量有效传递到1号塔、4号塔以及锚碇，增强结构的整体性，从而减小桥塔及加劲梁的变形，提高结构刚度。

在研究主缆的纵向受力时，图2，3所示的悬索桥可简化为图4所示的力学模型，主缆对桥塔的约束作用近似看作是具有一定刚度的弹簧。

悬索桥边跨主缆对桥塔的约束作用较强，边桥塔（最外侧桥塔）在活载作用下的变形远小于中间桥塔，多跨悬索桥的变形主要由中塔的纵向变形引起。中塔位移与桥塔本身刚度和桥塔之间的主缆纵向约束刚度有关，对于传统的悬索桥体系，主缆对桥塔的纵向约束作用已经有较为精确的解析解法[12-15]，文献[13]提供的主缆纵向约束刚度Kc的解析式为

Kc=3128g（Lf）3+gL4f

（2）

由式（2）可以看出，主缆的纵向约束刚度与恒载集度成正比，与垂跨比倒数的三次方近似成正比，传统悬索桥垂跨比的取值范围一般为1/12～1/9，这也就决定了主缆的纵向约束刚度存在一个大致范围。

双缆体系对桥塔的纵向约束刚度可以按式（3）求解[9]，即

Kc=L28δ（gt+aδft-bδ+gb-aδfb-bδ-gtft-gbfb）

（3）

a=316L（1ft-1fb）/[1EtAtu（nt）+1EbAbu（nb）]

（4）

b=3L16（1ft-1fb）/[1+EtAtu（nt）EbAbu（nb）]-3L16ft

（5）

u（n）=8（163n2-1285n4）/（1+83n2-325n4）

（6）

式中：gt，gb分别为上缆与下缆承担的恒载；δ为塔顶位移，计算时可取δ=0.01 m；ft，fb分别为双缆体系中上缆与下缆的垂度；Et，Eb分别为上缆和下缆的弹性模量；At，Ab分别为上缆和下缆的截面面积；nt，nb分别为上缆和下缆的垂跨比；n为主缆垂跨比，n=f/L。2 双缆体系与传统体系纵向刚度比较

由于双缆的纵向约束刚度受到多个参数的影响，为直观比较双缆与传统主缆纵向约束刚度的差异，假定主跨长度L=1 000 m，桥面恒载集度（不含主缆）为230 kN·m-1，分别计算传统悬索桥主缆体系与双缆体系纵向约束刚度以及主缆用钢量。

传统体系的主缆垂跨比取1/12～1/9。双主缆体系下缆垂跨比取为1/8～1/5，上缆垂跨比取为1/15～1/12，恒载在上缆与下缆的分配比例分别取为3∶7，4∶6，5∶5三种情况。主缆截面面积按恒载作用下主缆跨中的应力620 MPa确定。由式（2）求得传统悬索桥体系的主缆纵向刚度如图5所示，由式（3）求得双缆体系的纵向约束刚度如图6所示。

由图5可以看出，采用传统悬索体系，主缆垂跨比由1/9减小至1/12，主缆纵向约束刚度从5 MN·m-1增大至12.5 MN·m-1。由图6可以看出，随着上缆承担恒载比例的增大以及上下缆垂度差值的增大，主缆的纵向约束刚度从5.75 MN·m-1增大至31 MN·m-1。恒载在上缆分配的比例越大，双缆的纵向约束刚度越大；上缆垂度越小而下缆垂度越大时，双缆的纵向约束刚度越大。双缆的纵向约束刚度变化范围较大，其最大能够提供的纵向约束刚度远大于传统悬索桥体系，双缆的最大纵向约束刚度达到传统主缆刚度的2倍以上。

对于传统悬索桥体系，在恒载集度确定之后，主缆的纵向约束刚度仅受主缆垂跨比的影响。双缆体系的纵向约束刚度则要复杂得多，主要受到双缆的垂跨比、恒载在上缆与下缆之间的分配比例及主缆的轴向刚度等因素影响。由图6还可知，上缆与下缆的垂跨比差值越大（上缆垂度越小而下缆垂度越大），恒载分配给上缆的比例越大，双缆体系的纵向约束刚度越大[9]。3 主缆用钢量分析

双缆体系虽然在同一个索面内有垂度不同的2根主缆，并不意味着主缆用钢量多于传统的悬索桥体系，恰恰相反，由于下侧主缆可采用较大的垂度，恒载在下缆中引起的内力较小，上下主缆的内力之和甚至小于传统单根主缆悬索桥。因此，采用双缆体系的多跨悬索桥其主缆总用钢量不会多于传统体系的多跨悬索桥，主缆用钢量可按以下方法求解。

假定悬索桥主缆总体线形为抛物线，则其线形可表示为

y=-4fL2x（L-x）

（7）

主缆长度S可表示为

S=∫L0（1+y′2）dx=L（1+163n2）

（8）

令主缆截面面积为A，恒载引起的主缆跨中处应力为σ，则主缆水平力为

H=Aσ

（9）

单位桥长恒载由主缆荷载集度和桥面荷载集度（加劲梁及铺装）两部分构成，即

g=q+γA

（10）

式中：q为桥面荷载集度；γ为主缆重度。

将式（9），（10）代入式（1）得

Aσ=（q+γA）L28f

（11）

由式（11）得主缆截面面积为

A=qL28fσ-γL2

（12）

将主缆长度与截面面积进行相乘，可得每个主跨主缆的用钢量Q为

Q=AS=qL3（1+16n2/3）8fσ-γL2

（13）

由式（13）可知，在确定了桥面荷载集度q、主缆垂度f、跨长L、主缆重度γ以及恒载引起的主缆跨中处应力σ，即可由式（13）求得单跨主缆用钢量。

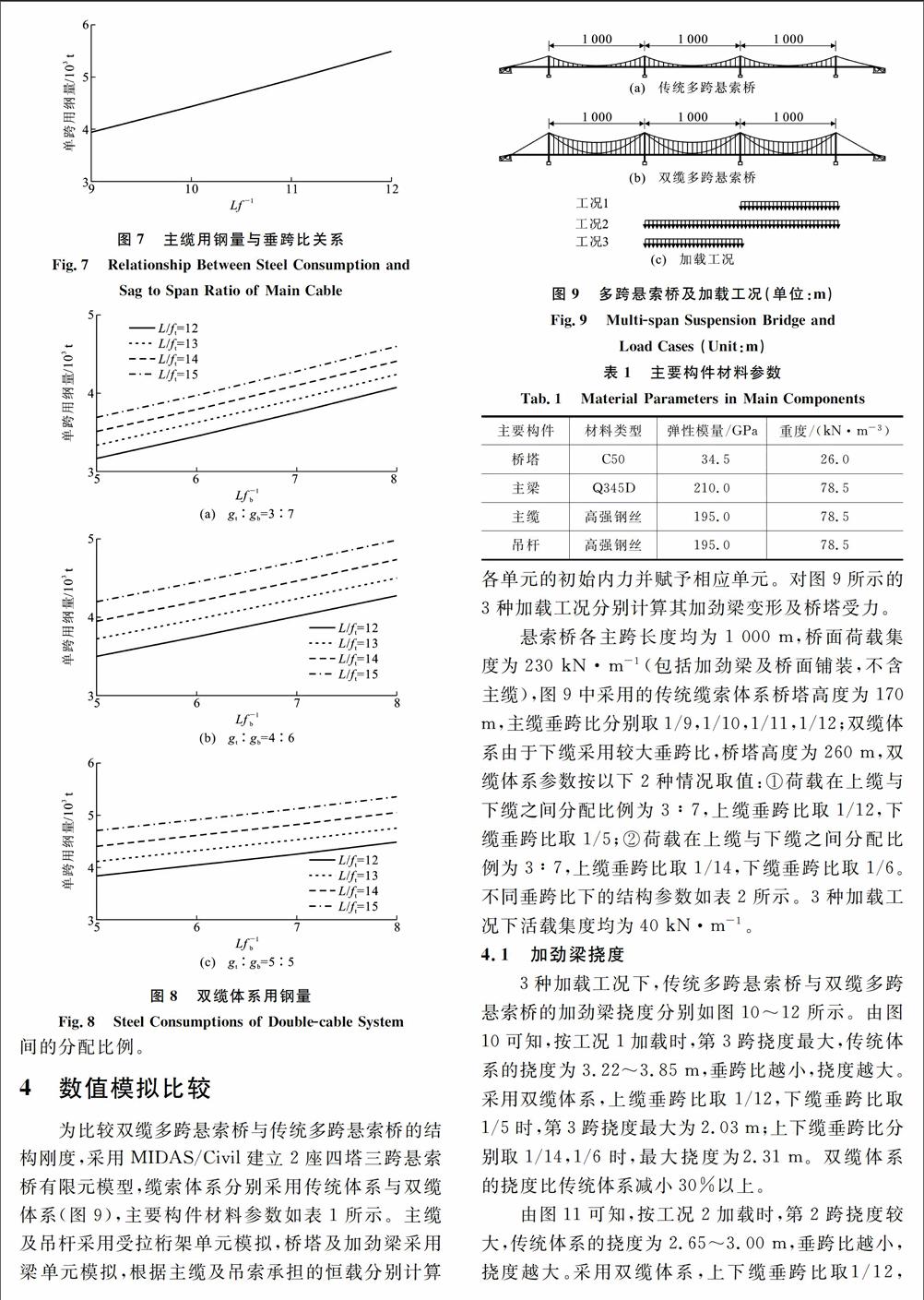
为直观比较传统悬索体系与双缆体系的主缆用钢量差异，假定桥面荷载集度为230 kN·m-1，令恒载作用下主缆应力为620 MPa，按照式（13）求得的传统缆索体系多跨悬索桥单跨的主缆用钢量如图7所示，双缆体系的单跨用钢量如图8所示。

由图7，8可以看出，传统单根主缆的悬索桥用钢量在4 000～5 500 t之间，而双缆体系用钢量在3 000～5 500 t之间。双缆体系与传统悬索桥体系的主缆用钢量均受垂跨比影响，垂跨比越小（L/f越大），主缆用钢量越多。双缆的用钢量还受荷载在上下缆之间分配比例的影响，上缆分配的恒载荷载集度越多，则双缆体系用钢量越大。这是因为主缆水平力主要取决于主缆垂跨比及荷载在上缆与下缆之间的分配比例。4 数值模拟比较

为比较双缆多跨悬索桥与传统多跨悬索桥的结构刚度，采用MIDAS/Civil建立2座四塔三跨悬索桥有限元模型，缆索体系分别采用传统体系与双缆体系（图9），主要构件材料参数如表1所示。主缆及吊杆采用受拉桁架单元模拟，桥塔及加劲梁采用梁单元模拟，根据主缆及吊索承担的恒载分别计算

各单元的初始内力并赋予相应单元。对图9所示的3种加载工况分别计算其加劲梁变形及桥塔受力。

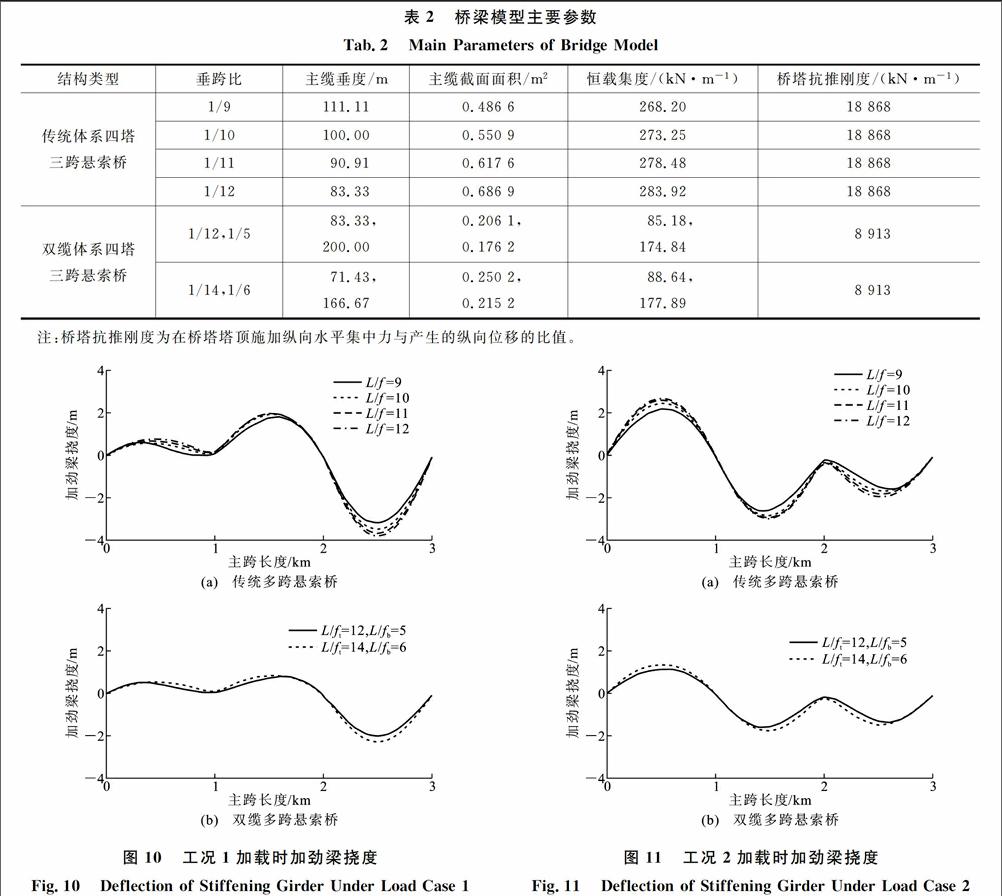
悬索桥各主跨长度均为1 000 m，桥面荷载集度为230 kN·m-1（包括加劲梁及桥面铺装，不含主缆），图9中采用的传统缆索体系桥塔高度为170 m，主缆垂跨比分别取1/9，1/10，1/11，1/12；双缆体系由于下缆采用较大垂跨比，桥塔高度为260 m，双缆体系参数按以下2种情况取值：①荷载在上缆与下缆之间分配比例为3∶7，上缆垂跨比取1/12，下缆垂跨比取1/5；②荷载在上缆与下缆之间分配比例为3∶7，上缆垂跨比取1/14，下缆垂跨比取1/6。不同垂跨比下的结构参数如表2所示。3种加载工况下活载集度均为40 kN·m-1。

4.1 加劲梁挠度

3种加载工况下，传统多跨悬索桥与双缆多跨悬索桥的加劲梁挠度分别如图10～12所示。由图10可知，按工况1加载时，第3跨挠度最大，传统体系的挠度为3.22～3.85 m，垂跨比越小，挠度越大。采用双缆体系，上缆垂跨比取1/12，下缆垂跨比取1/5时，第3跨挠度最大为2.03 m；上下缆垂跨比分别取1/14，1/6时，最大挠度为2.31 m。双缆体系的挠度比传统体系减小30%以上。

由图11可知，按工况2加载时，第2跨挠度较大，传统体系的挠度为2.65～3.00 m，垂跨比越小，挠度越大。采用双缆体系，上下缆垂跨比取1/12，

31/5时的挠度为1.61 m，上下缆垂跨比取1/14，1/6时挠度的为1.77 m，双缆体系的挠度比传统体系减小约40%。

由图12可知，按工况3加载时第2跨挠度最大，这也是整个结构挠度最大的加载工况，传统体系的挠度为4.39～4.94 m。采用双缆体系，上下缆垂跨比取1/12，1/5时，第2跨最大挠度为2.31 m；上下缆垂跨比分别取1/14，1/6时，最大挠度为2.61 m。双缆体系的挠度比传统体系减小40%以上。

采用传统体系的多跨悬索桥，主缆垂跨比越大，挠度越小。这是因为采用较小垂跨比时，虽然主缆的纵向约束刚度有所增大，但活载引起的水平力也会相应增大，并且在主缆垂度越小时，塔顶位移引起的主缆挠度越大[16]。

采用传统体系时，按照工况3加载的加劲梁挠度超过4 m，挠跨比大于1/250，结构刚度过低。采用双缆体系时，跨中最大挠跨比可控制在1/383，结构刚度满足要求。3种加载工况下，双缆体系的加劲梁挠度均比传统体系减小30%以上，结构最大挠度减小40%以上，由此可见，双缆体系有效提高了多跨悬索桥结构刚度。

4.2 桥塔受力

在本文模型中，双缆体系的桥塔抗推刚度约为传统体系抗推刚度的1/2（表2），在3种加载工况下，双缆体系塔顶位移均小于传统体系的多跨悬索桥，因此其塔底弯矩也比传统体系的悬索桥大幅减小。3种加载工况下采用传统多跨悬索桥体系和双缆多跨悬索桥体系桥塔的塔底弯矩见图13～15。

由图13～15可知，采用双缆体系的多跨悬索桥在3种加载工况下其塔底弯矩均远小于采用传统体系的悬索桥，弯矩下降40%～50%，这主要是双缆体系的纵向约束较强，加载跨的主缆水平力增量被传递到边桥塔以及锚碇，桥塔受到的不平衡水平力减小，因此塔底弯矩较小。由此可见，采用双缆体系的多跨悬索桥，在结构刚度提高的同时，桥塔及基础的受力也有所改善。

4.3 主缆用钢量

主缆截面面积按恒载状态下主缆跨中应力为620 MPa确定。图9所示传统体系的多跨悬索桥垂跨比从1/9减小至 1/12时，每个主跨主缆用钢量从3 492.3 t增大至5 490.4 t。若采用双缆体系，当上下缆垂跨比分别为1/12，1/5时，每个主跨主缆用钢量为3 164.1 t，当上下缆垂跨比分别为1/14，1/6时，每个主跨主缆用钢量为3 796.5 t。由此可见，双主缆悬索桥的主缆用钢量与传统悬索桥相当，若对主缆垂跨比及恒载在上下缆的分配比例进行优化，双缆体系的钢量甚至可以小于传统缆索体系的悬索桥。5 结 语

（1）双缆多跨悬索桥主缆的纵桥向约束刚度达到传统悬索桥的2～6倍，在多跨悬索桥的最不利加载工况下，采用双缆体系的多跨悬索桥的加劲梁挠度比传统体系有明显减小，双缆体系可以有效增大多跨悬索桥的结构刚度。

（2）双缆体系的多跨悬索桥在受到活载作用时，桥塔受到的不平衡水平力比传统悬索桥有明显减小，塔底弯矩降低40%～50%。由此可见，多跨悬索桥中采用双缆体系可降低桥塔下部结构造价。

（3）双缆体系的用钢量与传统悬索桥相当，若双缆体系中采用较大的下缆垂度，双缆体系的主缆用钢量甚至小于传统体系悬索桥。

参考文献：

References：

[1] 王 达，李宇鹏，刘 扬.大跨度悬索桥锚跨索股张力精细化控制分析[J].中国公路学报，2014，27（1）：51-56.

WANG Da，LI Yu-peng，LIU Yang.Analysis of Refinement Control of Anchor Cable Tension for Long-span Suspension Bridge[J].China Journal of Highway and Transport，2014，27（1）：51-56.

[2]李永乐，侯光阳，乔倩妃，等.超大跨径悬索桥主缆材料对静风稳定性的影响[J].中国公路学报，2013，26（4）：72-77.

LI Yong-le，HOU Guang-yang，QIAO Qian-fei，et al.Effects of Different Cable Materials on Aerostatic Stabilities of Super-long-span Suspension Bridges[J].China Journal of Highway and Transport，2013，26（4）：72-77.

[3]GIMSING N J.Cable Supported Bridges：Concept and Design[M].2nd ed.Chichester：John Wiley & Sons，1997.

[4]陈艾荣，陈文明.多跨悬索桥的性能[C]//中国公路学会.中国公路学会桥梁和结构工程学会2001年桥梁学术研讨会论文集.北京：人民交通出版社，2001：561-566.

CHEN Ai-rong，CHEN Wen-ming.Performances of Multi-span Suspension Bridge[C]//China Highway and Transportation Society.Proceedings of 2001 Symposium on Bridge，Bridges and Structures Society，China Highway and Transportation Society.Beijing：China Communications Press，2001：561-566.

[5]张新军，陈 兰，赵孝平.三塔悬索桥的缆索体系及其抗风稳定性[J].浙江工业大学学报，2010，38（4）：437-441.

ZHANG Xin-jun，CHEN Lan，ZHAO Xiao-ping.Cable System and Wind Stability of Three-tower Suspension Bridges[J].Journal of Zhejiang University of Technology，2010，38（4）：437-441.

[6]张劲泉，曲兆乐，宋建永，等.多塔连跨悬索桥综述[J].公路交通科技，2011，28（9）：30-45，52.

ZHANG Jin-quan，QU Zhao-le，SONG Jian-yong，et al.Overview of Multi-pylon Multi-span Suspension Bridge[J].Journal of Highway and Transportation Research and Development，2011，28（9）：30-45，52.

[7]柴生波，肖汝诚，孙 斌.双缆悬索桥体系的力学特性（Ⅰ）[J].华南理工大学学报：自然科学版，2011，39（12）：159-164.

CHAI Sheng-bo，XIAO Ru-cheng，SUN Bin.Mechanical Properties of Double-cable Suspension Bridge System（Ⅰ）[J].Journal of South China University of Technology：Natural Science Edition，2011，39（12）：159-164.

[8]柴生波，肖汝诚.双缆悬索桥体系的力学特性（Ⅲ）[J].华南理工大学学报：自然科学版，2013，41（8）：120-126.

CHAI Sheng-bo，XIAO Ru-cheng.Mechanical Properties of Double-cable Suspension Bridge System（Ⅲ）[J].Journal of South China University of Technology：Natural Science Edition，2013，41（8）：120-126.

[9]CHAI S B，XIAO R C，LI X N.Longitudinal Restraint of a Double-cable Suspension Bridge[J].Journal of Bridge Engineering，2014，19（4）：111-122.

[10]GIMSING N J，GEORGAKIS C T.Cable Supported Bridges：Concept and Design[M].3rd ed.Chichester：John Wiley & Sons，2012.

[11]肖汝诚.桥梁结构体系[M].北京：人民交通出版社，2013.

XIAO Ru-cheng.Bridge Structural Systems[M].Beijing：China Communications Press，2013.

[12] YOSHIDA O，OKUDA M，MORIYA T.Structural Characteristics and Applicability of Four-span Suspension Bridge[J].Journal of Bridge Engineering，2004，9（5）：453-463.

[13]柴生波，肖汝诚，张学义，等.多跨悬索桥中塔纵向刚度研究[J].中国公路学报，2012，25（2）：67-71.

CHAI Sheng-bo，XIAO Ru-cheng，ZHANG Xue-yi，et al.Study of Longitudinal Stiffness of Middle Pylon in Multi-span Suspension Bridge[J].China Journal of Highway and Transport，2012，25（2）：67-71.

[14]KIUREGHIAN A D，SACKMAN J L.Tangent Geometric Stiffness of Inclined Cables Under Self-weight[J].Journal of Structure Engineering，2005，131（6）：941-945.

[15]CHOI D H，GWON S G，NA H S.Simplified Analysis for Preliminary Design of Towers in Suspension Bridge[J].Journal of Bridge Engineering，2014，19（3）：165-184.

[16]柴生波，肖汝诚，孙 斌.活载下悬索桥主缆变形特性[J].同济大学学报：自然科学版，2012，40（10）：1452-1457.

CHAI Sheng-bo，XIAO Ru-cheng，SUN Bin.Deformation Characteristics of Main Cable in Suspension Bridge Caused by Live Load[J].Journal of Tongji University：Natural Science，2012，40（10）：1452-1457.