电机学难点教学的多思维融合方法

黄洪全 任家富 陈光柱

摘要：“电机学”内容多，难度大，按传统单一教学方法难以达到好的教学效果。以旋转磁场性质的教学为例，采用数学公式、时间波形、空间波形、绕组空间位置、磁场矢量及磁场形象化相结合的多思维融合方法来帮助理解，能做到感性与理性、具体与抽象的统一，会加快和加深对相关知识的掌握，让学生在课堂上“愉快”地学习，大大提升教学质量。

关键词：电机学；教学；多思维；融合

中图分类号：G642.0 文献标志码：A 文章编号：1674-9324（2015）10-0183-02

“电机学”课程作为电气工程自动化专业的一门核心课程[1]，它以多个学科为基础，知识点多，而且抽象、难于理解。学生以前对电机实际运行知之甚少，若仅按单一的思维方法进行知识点的讲授，很难达到预期的教学效果[2]。譬如，针对旋转磁场这种难以理解的知识点，仅从数学公式递推的思维方法讲解旋转磁场的时间和空间函数性质，即便通过多次反复推导让学生明白数学公式的演变过程，仍然难以将电机绕组空间分布、交变电流与磁场之间的关系贯通[3，4]，对原理的阐述必定显得生硬，令人感到枯燥乏味，学生学习的积极性和主动性备受打击，不利于发挥学生学习的潜能，也不利于学生能力的培养，难免课程结束后绝大部分学生对“电机学”内容一知半解甚至对其最基本原理都难以理解。实际上，“电机学”是理论与实际工程设备对象——电机的统一，是抽象性与具体性的统一，在教学中不仅要将理论学习与实验操作进行结合[5]，针对难点还要用多种思维方法来帮助理解，做到由浅入深、由感性到理性、由具体到抽象。比如可以采用数学公式推导、磁场几何向量的演变、不可见磁场的可视化等来阐述旋转磁场性质，定会加快和加深对相关知识的理解，让学生在课堂上“愉快”地学习，这将大大提升教学质量。由于旋转磁场内容在“电机学”中是重点和难点，故下面就以旋转磁场性质知识点为例，谈谈如何做到采用多种思维方法来帮助理解并最终提高教学效率和教学质量。首先简要叙述旋转磁势的性质。

一、旋转磁势的难点

当对称的三相交流绕组流过三相对称交流电流时，无论电流是由电源提供还是感应产生，合成磁势为一旋转磁势。对旋转磁势教学的难点在于：三相合成磁势的振幅为每相脉动磁势振幅的3/2倍；同步转速n1=60f/p（r/min），f和p分别为电流频率（单位Hz）和电机的极对数；三相合成磁势的振幅位置随时间的变化与绕组电流关系。

二、思维一：数学公式推导

单相绕组流过交流电产生的脉动磁势是随时间按正弦规律变化的，可以按下式分解为两个旋转磁势分量。每个旋转磁势的振幅为脉动磁势振幅的一半，旋转速度相同，旋转方向相反。

f1=Fm1sinωtsinx=■Fm1cos（ωt-x）+■Fm1cos（ωt+x-π） （1）

三相对称交流绕组流过三相对称电流时，假设三相电流为ia=■Isinωt，ib=■Isin（ωt-120°），ic=■Isin（ωt+120°）；通过推导三相绕组合成磁势的基波为■Fm1cos（ωt-x）。三相对称电流的脉动磁势分解为6个旋转磁场，其中三个磁场极性方向相差120°，它们的转动方向和转速一致而抵消。另三个磁场的极性方向、转动方向及转速一致而相加，得到的总磁场振幅为单相绕组脉动磁势的1.5倍，且为旋转磁场。

三、思维二：时间波形、空间波形与绕组空间位置的结合

按思维一对脉动磁势及其分解加以理解并不直观，公式得出的总磁场的时间空间函数性质与旋转磁场性质并不太容易完全对上号。

对于公式（1）中的脉动磁势的时间空间性质，如将圆周空间位置x变为直线坐标，将多个固定时刻磁场随x的变化规律用波形表达将会更为直观，比如选取ωt=π/2，π，3π/2等时刻。对于固定的空间位置x，该处磁场随时间按正弦规律变化；而对于固定时刻，磁场随空间位置x的变化规律为正弦关系。磁场幅值位置不随时间变化，不旋转，但幅值大小随时间按正弦变化。脉动磁势分解后得到的每个磁场分量仍然是时间空间函数，对于固定的空间位置x，该处磁场仍然随时间按正弦规律变化；对于固定时刻，磁场随位置x的变化规律仍为正弦关系，磁场幅值位置随时间移动，磁场幅值大小不变，即旋转磁场，且两磁场旋转方向相反。当三相对称交流绕组流过三相对称电流时，采用如上分解为六个磁场，从波形的叠加不太容易看出合成磁场的性质。如取三个时刻，需要画出27个波形，不太方便，直观性降低，需改变思路。

将三相电流的时间波形与绕组的空间分布相结合，并示意出磁场随时间在空间位置上的变化，采用这样的思维方法来分析，非常容易得出合磁场的旋转性质。设三相对称电流为i■，i■，i■，若i■为正，则电流由U1端进U2端出，电流i■，i■类似。选取几个关键时间点ωt=0，2π/3，4π/3，2π时刻，合磁场的方向分别在U，V，W，U绕组轴线上，每隔ωt=2π/3的时间合磁场的方向由U轴转向V轴，V轴转向W轴，再由W轴回到U轴，如此反复。当磁极对数p=1时，相邻两相绕组在空间位置相差2π/3；当磁极对数p=2时，相邻两相绕组在空间位置相差π/3；当磁极对数p=m时，相邻两相绕组在空间位置相差2π/3m。可推知，在一个通电周期磁场旋转1/p圆周，同步转速n1=60f/p（r/min）。当某相电流达到最大值时，其余两相电流为1/2，合成磁场为单相振幅的1.5倍。旋转磁场的其他性质容易直观得知。

四、思维三：磁场矢量、磁场形象化及绕组空间分布的结合

用矢量长短表示磁场强弱，方向代表该绕组脉振位置（或磁场方向），脉振磁场的分解用等式表示，如A=B+C，等号左边的矢量随时间长短发生变化，没有转动，等号右边相加的两矢量随时间长短不发生变化但反方向转动，二者之和等于脉振磁场。形象地画出脉振磁场及其分解，依然如A=B+C的形式，只是与矢量表示的区别在于用形象的N-S磁铁，磁铁长短表示磁场强弱，更为直观形象地表达了脉振磁场及其分量的性质。

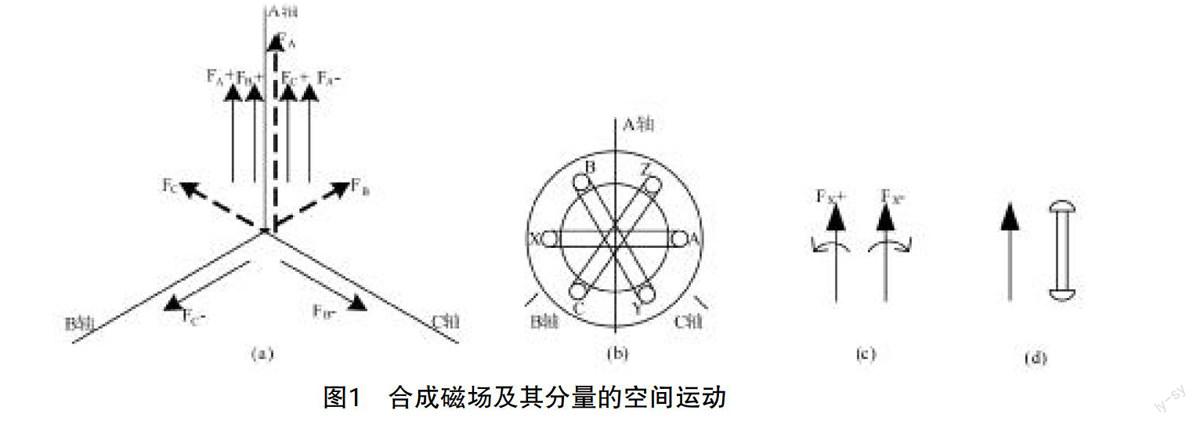
如图1所示为合成磁场及其分量的空间运动，FA+，FB+，FC+分别为A，B，C三相正分量，三者磁场方向始终一致，同方向旋转（图中为逆时针），合成为总磁场；FA-，FB-，FC-分别为A，B，C三相负分量，三者磁场方向始终成120°，同方向旋转（图中为顺时针），相抵后合成磁场为零。FA+与FA-合成为A相脉振磁场FA，FB+与FB-合成为B相脉振磁场FB，FC+与FC-合成为C相脉振磁场FC。FA，FB，FC分别在各相的绕组轴线上，方向与轴线相同或相反。假设通电相序为A-B-C，绕组分布如图（b）所示，相电流为最大值的绕组其磁势为最大值“1”，另两绕组其磁势均为“0.5”，三者合成磁势为“1.5”，方向由电流为最大值的相绕组决定。随着各向量的空间运动，合成磁势顺时针旋转，同步转速n1=60f/p（r/min），按“思维二”进行分析，其他性质也容易得出。

五、结束语

“电机学”内容多，难度大，按传统数学推导的单一教学方法难以达到好的教学效果。“电机学”是理论与实际工程设备对象——电机的统一，是抽象性与具体性的统一，若在教学中针对难点采用多种思维方法来帮助理解，比如，对于旋转磁场性质的教学，采用数学公式推导，时间波形、空间波形、绕组空间位置、磁场矢量及磁场形象化相结合，做到由浅入深、由感性到理性、由具体到抽象，定会加快和加深对相关知识的理解，让学生在课堂上“愉快”地学习，这将大大提升教学质量。

参考文献：

[1]胡虔生，等.电机学[M].北京：中国电力出版社，2008.

[2]杨泽斌，孙玉坤，谭伦农.电气工程及其自动化专业实践教学的探索与思考[J].电气电子教学学报，2007，29（1）：69-71.

[3]谢宝昌.交流电机绕组的气隙磁势与电势计算[J].电气电子教学学报，2014，36（2）：39-42.

[4]聂晶，王洪坤，柴兆森，胡春玲，等.“电机学”中电磁场基础理论教学的探索与实践[J].中国电力教育，2013，273（14）：53-54.

[5]刘瑞芳.交流电机旋转磁场的教学研究[J].电气电子教学学报，2011，33（5）：82-84.