关于圈图Cn的连3距k着色计数

薛展充

（澳门培正中学，澳门）

关于圈图Cn的连3距k着色计数

薛展充

（澳门培正中学，澳门）

研究圈图Cn的连3距k着色计数问题，根据图的特征及基本计数原理建立若干联立递推关系，由此得到关于圈图Cn的连3距k着色方法数的递推关系.

圈；路；图的连3距k着色

0 引言

对图G的每个顶点都指定一种颜色，使得没有两个相邻的顶点指定为相同的颜色.如果这些颜色选自于一个有k（k≥3）种颜色的集合而不管k种颜色是否都用到，这样的着色称为k着色[1].

图的染色计数问题已有很多研究结果，如棋盘的染色计数公式[2-5]，n棱伞图的k着色计数公式[6]，圈图的染色计数公式[7]，有公共顶点的圈的染色计数公式[8]，圈图的连2距k着色计数公式[9]，本文拟进一步对圈图Gn的连3距k着色计数问题进行研究，先给出以下定义.

定义1[10]图G的一条途径（或通道）是指一个有限非空序列W=ν0e1ν1e2ν2…enνn，它的项交替地为顶点和边，使得对1≤i≤n，ei的端点是νi-1和νi，称W是从ν0到νn的一条途径，或一条（ν0，νn）途径.ν0和νn分别称为W的起点和终点，而ν1，ν2，…，νn-1称为它的内部顶点.整数n称为W的长.若途径W的边e1，e2，…，en互不相同，则W称为迹.又若途径W的顶点ν0，ν1，…，νn也互不相同，则W称为路.长为n的路称为n路，记为Ln.

定义2[10]G的两个顶点u和ν称为连通的，如果在G中存在（u，ν）路.若在G中顶点u和ν是连通的，则u和ν之间的距离dG（u，ν）是G中最短（u，ν）路的长.

定义3[10]称一条途径是闭的，如果它有正的长且起点和终点相同.若一条闭迹的起点和内部顶点互不相同，则它称为圈.长为n的圈称为n圈，记为Cn.

定义4对图G的每个顶点都指定一种颜色，使得任意距离不大于3的两点均异色.如果这些颜色选自于一个有k（k≥4）种颜色的集合而不管k种颜色是否都用到，这样的着色称为图G的连3距k着色.

以g3（k，G）表示图G的连3距k着色的着色方法数，则g3（k，Gn）表示圈图Cn（n≥4）的连3距k着色的着色方法数.设圈图Cn（n≥4）的n个顶点分别为A1，A2，A3，…，An，把Cn从顶点A1与顶点An之间割开，使成长为n-1的路Ln-1，则有g3（k，Ln-1）＝k（k-1）（k-2）（k-3）n-3，其中A1与An-2，An-1，An都异色且A2与An-1，An都异色且A3与An异色的着色方法数即为g3（k，Cn）.

g3（k，Ln-1）包括以下十五类情况（见表1）：

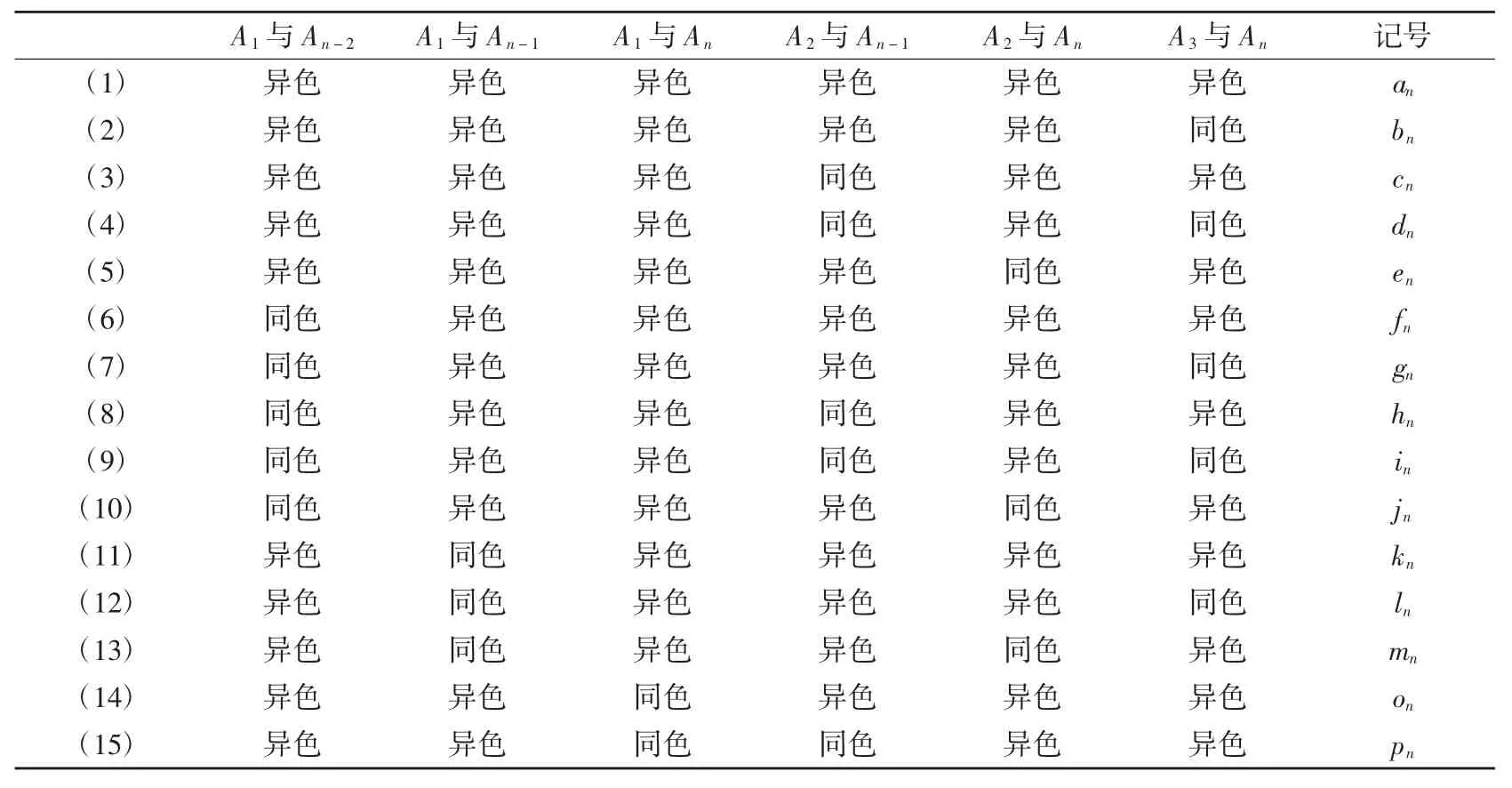
表1 g3（k，Ln-1）包含的十五类情况

易知an=g3（k，Cn），in=an-3.由对称性，bn=cn=fn，dn=hn，en=kn，jn=ln，故

an+an-3+3bn+2dn+2en+gn+2jn+mn+on+pn=k（k-1）（k-2）（k-3）n-3，n≥7.

1 相关引理和定理

引理1设g3（k，Ln-1）中A1与An-2，An-1，An都异色的染色方法数为yn，则

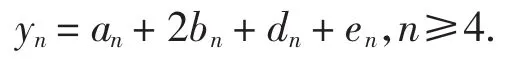
证明g3（k，Ln-1）中A1与An-2，An-1，An，都异色即表1中的（1）至（5）类情况，由加法原理即得所证.

引理2 yn+yn-1+（k-3）yn-2+（k-3）2yn-3=k（k-1）（k-2）（k-3）n-3，n≥7.

证明把g3（k，Ln-1）分成下列四类：

（1）A1与An-2，An-1，An都异色，此时的染色方法数为yn；

（2）A1与An同色且A1与An-2，An-1都异色，此时的染色方法数为yn-1；

（3）A1与An-1同色且A1与An-2，An都异色，此时的染色方法数为（k-3）yn-2；

（4）A1与An-2同色且A1与An-1，An都异色，此时的染色方法数为（k-3）2yn-3.

由加法原理即得所证.

引理3 bn+gn+jn=（an-3+bn-3）（k-4）（k-3）+（bn-3+en-3+dn-3）（k-3）2，n≥7.

证明由对称性，g3（k，Ln-1）中A1与An-2同色且An与A2，A3均无染色限制的染色方法数为bn+gn+jn，此染色方法数可分为下列五类（见表2）：

表2 bn+gn+jn包含的五类情况

由加法原理即得所证.

引理4 en+jn+mn=（an-2+2bn-2+dn-2+en-2）（k-3），n≥6.

证明由对称性，g3（k，Ln-1）中A1与An-1同色且An与A2，A3均无染色限制的染色方法数为en+jn+mn，此染色方法数可分为下列五类（见表3）：

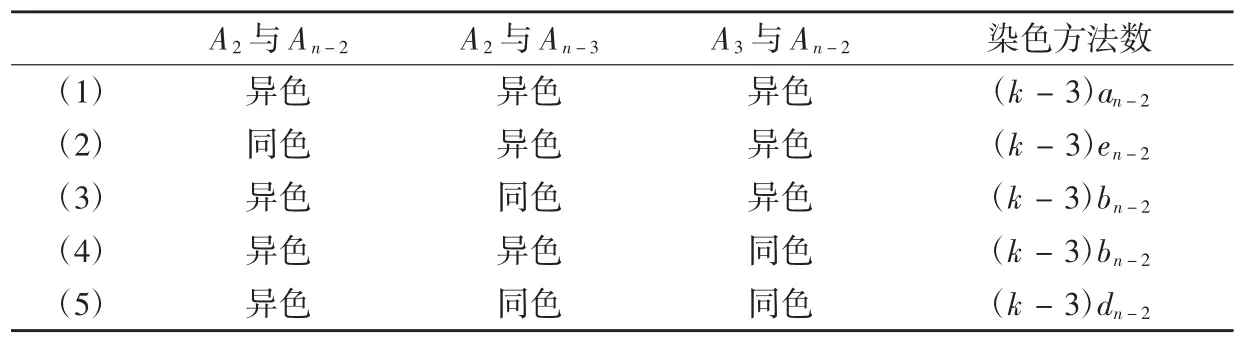
表3 en+jn+mn包含的五类情况

由加法原理即得所证.

引理5 on+pn=an-1+2bn-1+dn-1+en-1=yn-1，n≥5.

证明g3（k，Ln-1）中A1与An同色且A2与An-1染色限制的染色方法数为on+pn，此染色方法数可分为下列五类（见表4）：

表4 on+pn包含的五类情况

由加法原理即得所证.

引理6 dn=（k-4）an-3+（k-3）bn-3，n≥7.

证明把dn分成以下两类：（1）A1与An-2同色且A2与An-1同色且A3与An-3异色，

此时的染色方法数为（k-4）an-3；（2）A1与An-2同色且A2与An-1同色且A3与An-3同色，此时的染色方法数为（k-3）bn-3.

由加法原理即得所证.

引理7 en=（k-4）（an-2-an-3）+（2k-7）（bn-2-bn-3）+（k-3）（dn-2-dn-3）+（k-3）en-2，n≥7.

证明由引理3至5及

由引理1，2可得

再由引理6即得所证.

引理8设an中满足A1与An-3异色的染色方法数为qn，满足A1与An-3同色的染色方法数为rn；设en中满足A2与An-2异色的染色方法数为sn，满足A2与An-2同色的染色方法数为tn，则

证明把bn分成以下十类（见表5）：

表5 bn包含的十类情况

由加法原理得

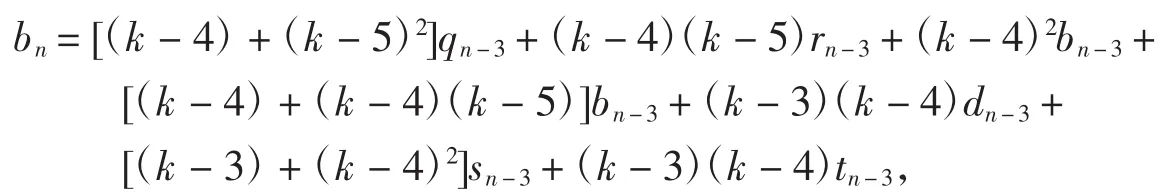
再由yn=an+2bn+dn+en，an=qn+rn，en=sn+tn，化简得即得所证.

引理9 en=（k-4）yn-2+dn-2+en-2-qn-2-sn-2，n≥6.

把cn分成以下七类（见表6）：

由加法原理得

表6 cn包含的七类情况

再由yn=an+2bn+dn+en，an=qn+rn，en=sn+tn，化简得即得所证.

引理10 bn=（k2-9k+20）an-3+（2k2-16k+31）bn-3+（k-3）（k-4）dn-3+（k-3）（k-4）en-3+（k-4）an-4+（2k-7）bn-4+（k-3）dn-4，n≥8.

证明由引理8，9化简即得所证.

引理11 an，bn，yn满足以下联立递推关系（n≥10）：

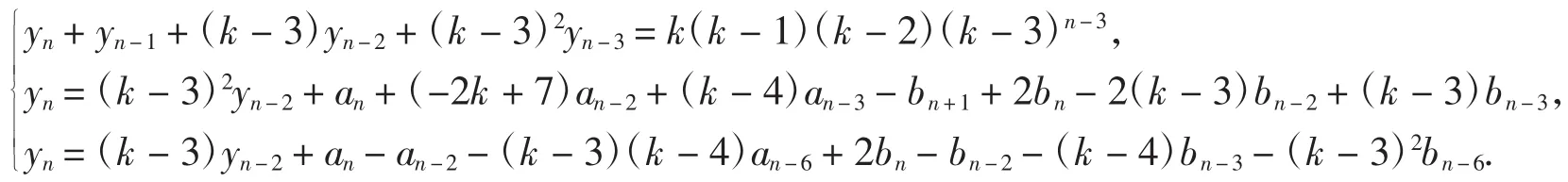
证明由引理1，2，6，7，10，通过加减消去法即得所证，过程较繁复，略.

定理1圈图Cn的连3距k着色方法数an满足以下递推关系：

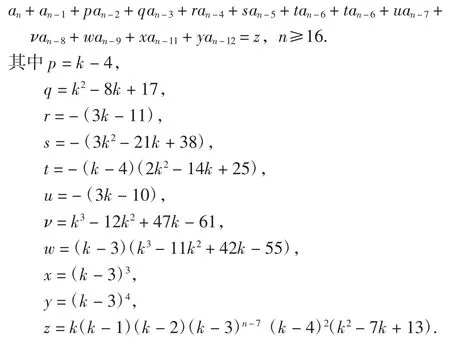
证明由引理11，通过加减消去法解联立递推关系可得所证，过程极为繁复，略.

至此本文得到关于圈图Cn的连3距k着色方法数an的递推关系，对于更高阶的圈图Cn的连m（m>3）距k着色问题，求解过程必更复杂，适当利用计算器辅助及探求图论新方法将是可取的.以下列出部分an值（见表7）.

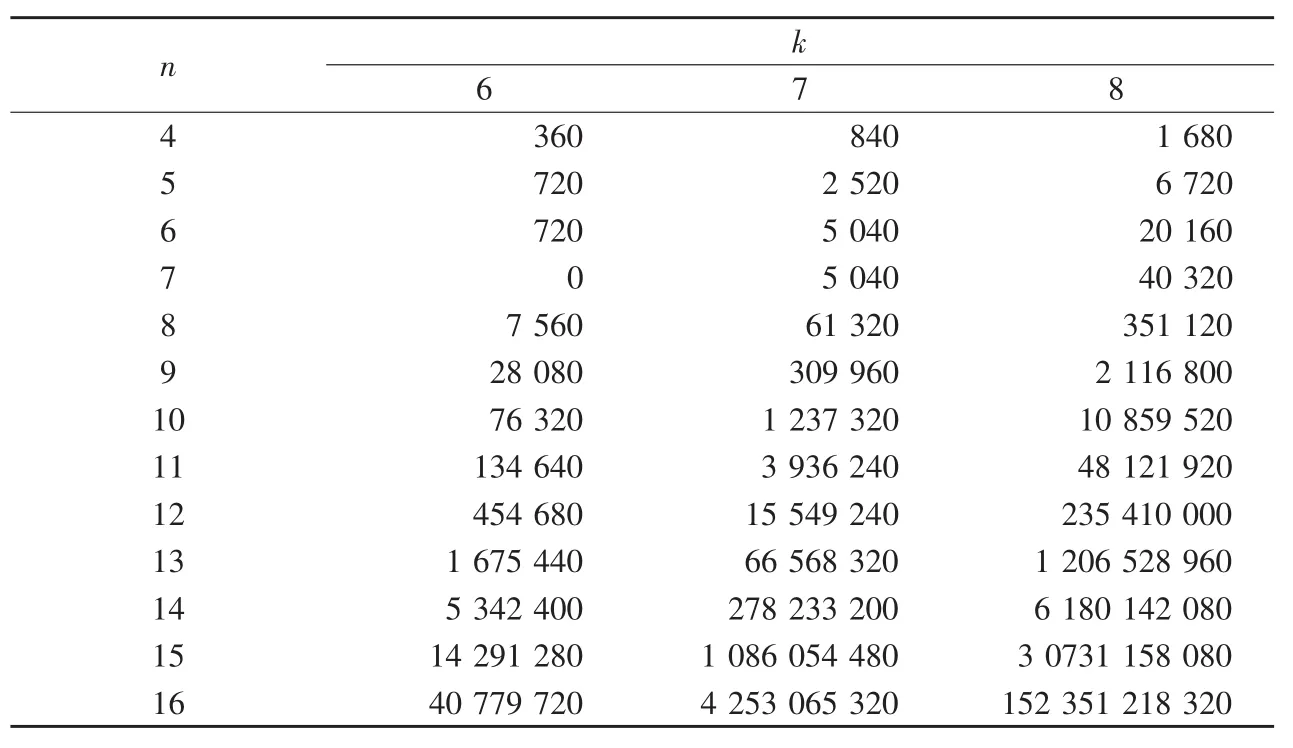
表7 部分an值

[1]殷剑宏，吴开亚.图论及其算法[M].合肥：中国科学技术大学出版社，2003：146.

[2]王跃进，牛伟强.关于2×n方格的染色问题研究[J].中学数学育，2011（1）：47-48.

[3]顾红俏.关于3×n棋盘的染色计数公式[J].新疆师范大学学报：自然科学版，2007，26（03）：90-92.

[4]卢家华，吴康.3×n方格染色问题的再研究[J].数学通报，2014，53（1）：61-63.

[5]张上伟，吴康.4×n棋盘的染色计数问题分析[J].汕头大学学报：自然科学版，2013，28（02）：1-3.

[6]卢家华，凌明灿，吴康.n棱伞图的k着色计数问题[J].汕头大学学报：自然科学版，2014，29（02）：1-3.

[7]范思琪，吴康，李祥立.从一个图论问题谈高考与竞赛的关系[J].澳门教育，2004，2：58-61.

[8]凌明灿，卢家华，吴康.有公共顶点的圈染色计数问题[C]//广东省初等数学学会成立大会暨首届学术研讨会论文集.广州：[出版者不详].2014.

[9]吴康，薛展充.关于圈图Cn的连2距k着色计数[J].华南师范大学学报：自然科学版，2007（2）：7-10.

[10]邦迪J A，默蒂U S R.图论及其应用[M].北京：科学出版社，1984：12-15.

Counting of Triple Distanced K-Coloring in Cycle

XUE Zhanchong
（Pui Ching Middle School,Macau,China）

The counting of triple distanced k-coloring in cycle is investigated.Some simultaneous recurrence relations are obtained according to the feature of the graph and fundamental counting principle.Thus，the recurrence relation about the counting of triple distanced k-coloring in cycle is obtained.

cycle；path；triple distanced k-coloring

O 167

A

1001-4217（2015）02-0056-06

2014-12-23

薛展充（1982-），男，澳门人，澳门培正中学高中数学老师.E-mail：sitsit_home@163.com