创意平板折叠桌的建模与分析
孙发军,张猛,杜月浩,曾良如
(怀化学院数学与计算科学学院,湖南怀化418008)
创意平板折叠桌的建模与分析
孙发军,张猛,杜月浩,曾良如
(怀化学院数学与计算科学学院,湖南怀化418008)
为解决目前市面上出现的一种创意折叠桌的自动设计问题,先讨论了简单常用圆形折叠桌的建模问题,用微元法通过桌面边缘点及桌面与桌脚夹角的关系建模得到折叠桌桌脚的动态变化模型.由此可求出圆形折叠桌的开槽位置及长度等加工参数.随后从稳固性、加工便利性、耗材等方面讨论了加工参数的优化设计.发现对于桌面形状任意的创意折叠桌,只要用户给出桌面边缘曲线,都可以建模计算出一组稳固性、耗材和耗工优化的加工参数,并以椭圆形折叠桌为例讨论了给定高度和宽度的椭圆折叠桌的建模计算.最后,讨论了折叠桌的建模仿真并给出了关键仿真代码.
折叠桌;优化模型;加工参数;Matlab仿真
1 引言
目前市场上出现一种创意平板折叠桌[1],桌面呈圆形,桌腿随着铰链的活动可以平摊成一张平板.桌腿由若干根木条组成,分成两组,每组各用一根钢筋将木条连接,钢筋两端分别固定在桌腿各组最外侧的两根木条上,并且沿木条有空槽以保证滑动的自由度.桌子外形由直纹曲面[2]构成,造型美观.为实现其批量和定制生产,我们需要为其建立求解加工参数的数学模型,以便可据给定板材的长宽设计出满足用户需求的各种创意桌来.目前已有众多建模爱好者对其展开研究,如安徽财经大学的朱家明、西安航空学院的刘睿等人的研究[3,4],但现有这些研究建立的模型多为连续模型不利于数值计算,计算速度较慢,且桌腿多为2D仿真,仿真效果不够逼真.为了建立求解速度更快的离散模型及得到高逼真的3D仿真,我们分成以下三方面来建模求解:
1)根据给定的长方形平板尺寸的相关数据来建立给定高度圆型折叠桌的数学模型,并求解计算出折叠桌的设计加工参数(例如桌腿木条开槽的长度)和桌脚边缘线的数学描述.
2)从产品稳固性好、加工便利、用材少等方面对于任意给定的折叠桌高度和圆形桌面直径的设计要求讨论长方形平板材料和折叠桌的最优设计加工参数,例如,平板尺寸、钢筋位置、开槽长度等.
3)根据客户任意设定的折叠桌高度、桌面边缘线的形状大小和桌脚边缘线的大致形状,给出所需平板材料的形状尺寸和切实可行的最优设计加工参数,使得生产的折叠桌尽可能接近客户所期望的形状.
2 问题分析
2.1 特定圆形折叠桌的分析
为方便问题的分析讨论,我们以桌底面中心为原点,xoy平面与桌底面重合,且x轴垂直木条指向桌面外侧,y轴平行桌面指向桌子左侧,z轴指向桌子下方,建立三维坐标.
首先需要建立模型描述该折叠桌的动态变化过程,即需要给出桌脚所在直纹曲面在折叠过程中的变化,为了简化问题的求解,我们采用微元法,外侧桌角与桌面的夹角α为参考,用桌角底边缘点Li的变化来描述变动的过程,首先假定桌面圆形恰好切中桌面两侧的短木条,且通过每根木条的中心点,如图1所示.则由圆桌面半径r及木条的宽度ws,可计算出最短木条一半的长度,从而确定图1中最下边木条右底端中心点D0的坐标;按同样的方法确定D0,D1…Dn(问题中n=19)的坐标,事实上不只是圆,对于能给出极坐标的曲线,都是很容易确定出D0,D1…Dn的坐标,即便是任意绘制的曲线,只要用木条去微分,使桌缘边线过木条两端中心,也很方便求出端点坐标,这样更利于我们第三问的求解.求得D0后可由之得出最外边的桌腿的长度lf0,即为平板长的一半减去D0的y坐标,从而根据桌腿侧面图(如图2),计算出外边桌腿与桌面夹角α的值.
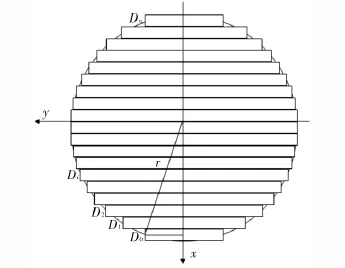
图1 桌面微分示意图
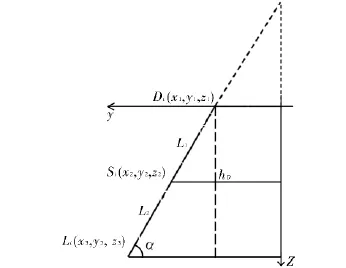
图2 桌脚底边缘线求法
为了确定桌脚的边缘线,可先求出桌脚顶端点Di和钢筋连接点Si的坐标,由之再根据桌腿长lf求出桌腿边缘点的坐标,由这些点的坐标即拟合出桌脚边缘线的数学描述.而桌脚顶端与桌面边缘点坐标相同,只需求钢筋所在点坐标即可.又由于钢筋是平行于xoy平面且与x轴平行,与y轴、z轴垂直的直线,由题意钢筋固定在桌腿前外侧木条的中心位置,故由图2可知能求出该直线的方程,进而由木条的x坐标求出相应的y坐标获得钢筋与各木条中点的交点坐标,此后,因桌脚边缘的点都在Di和Si点组成的直线上,因此容易由之利用腿长求得Li的坐标.再利用平铺时钢筋的起始位置和支起时钢筋所在位置的差值即可求出木条开槽长度、起始开槽位置、桌缘切割位置.
最后由Li的坐标可以拟合出桌脚底端边缘线.同时据所求数据即可用Matlab模拟出所设计的桌子.
2.2 圆形折叠桌的优化设计分析
然后我们从产品稳固性、加工便利性、耗材等方面讨论折叠桌的最优设计模型,具体分析如下.
2.2.1 稳固性分析
稳固性好主要可以从往桌上搁置重物时桌子的稳固性来考虑,主要可以考虑桌子是否侧翻和坍塌.对于侧翻主要考虑往脚折叠的两侧侧翻(即图1中的y轴方向),坍塌则是指折叠脚向两侧收回成平板的情况.而考虑通过调整桌脚与桌面的夹角来确保不会坍塌,或坍塌可能性要小些,很明显当α=90°,即桌脚与桌面垂直时,受力最大,不易坍塌,但侧翻可能性大,而当α较小时则容易因受重坍塌.故为简化模型,我们考虑两侧桌脚长度比桌面直径2r大时,我们认为桌子底盘稳固,不易侧翻,本文中取相等来计算.
2.2.2 加工便利性分析
因桌面锯腿每种设计方式都是必须工序,所以加工方便也就是考虑桌腿开槽的长度,槽越长愈费工,愈短愈省工.但要注意的是槽长影响到角度α,进而影响到桌子底盘大小,槽开的愈短,愈可能坍塌,愈长时则可能侧翻,所以也应适中为好.
2.2.3 耗材分析
对于指定桌面宽度的桌子,其用材就只决定于平板长度了,而用材需要根据桌高和角度及槽长来确定.桌越高,平板需要越长,角度α越小则要达到相同高度时需要的平板也越长.
2.3 折叠桌设计软件的建模分析
由题意要求设计出的软件数学模型能根据客户任意设定的折叠桌高度、桌面边缘线的形状大小和桌脚边缘线的大致形状可以计算出桌缘各木头的截断点,再由钢筋直线可求出桌脚下缘线,进而可以求出开槽的长度等设计加工参数[5].事实上,我们问题一中的分析表明,该题中建立的模型可适用于本问题的解决,只是要把圆曲线替换成客户任意设定的桌面边缘线即可.
3 模型假设与符号说明
3.1 模型假设
(1)假设桌子立起后有锁栓等将中间桌脚锁定;
(2)假设桌子的木条为无缝对接.
3.2 符号和相关术语说明
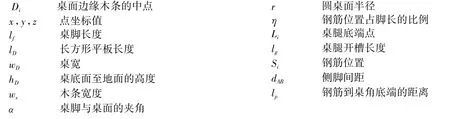
4 模型建立与求解
4.1 特定圆形折叠桌的建模及求解
4.1.1 圆形折叠桌的建模
设平板长度为lD,钢筋位置在Si,则可由迭代式(1)可求出桌面边缘点的坐标:
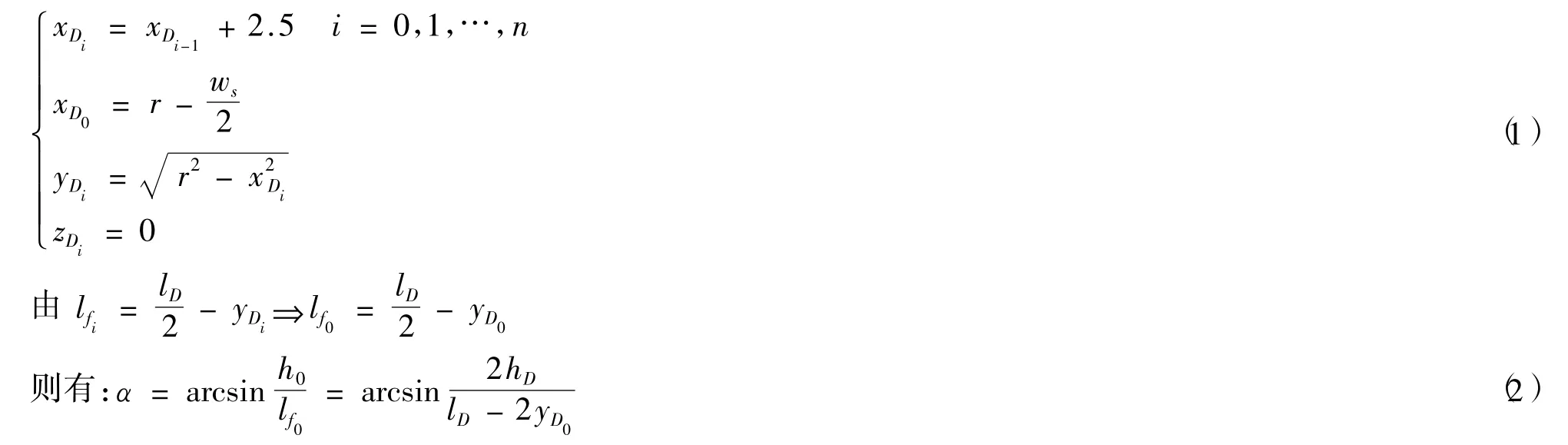
钢筋直线方程为:
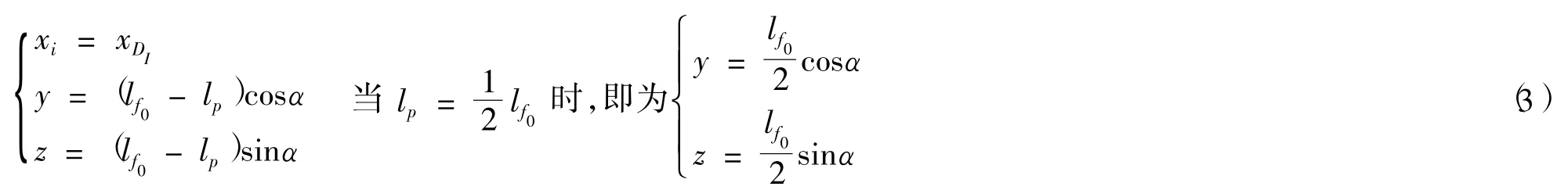
则由Di和Si的坐标可求出Li的坐标,首先由式(4)、(5)计算出如图2.4所示的l1,l2:

假设Di,Si,Li的坐标分别为(x1,y1,z1),(x2,y2,z2),(x3,y3,z3),
为方便计算,不妨令l1=|DiSi|,l2=|SiLi|

同理可求出y3,z3.
由上式可计算出折叠桌的动态变化过程Li的坐标如下:

4.1.2 圆形折叠桌的模型求解
不妨设长方形平板尺寸为120×50×3 cm,每根木条宽2.5 cm,连接桌腿木条的钢筋固定在桌腿最外侧木条的中心位置,折叠后桌子的高度为53 cm.
依据式(1)-(7),可以求得开槽长度、位置及桌缘切割位置等设计加工如表1所示.
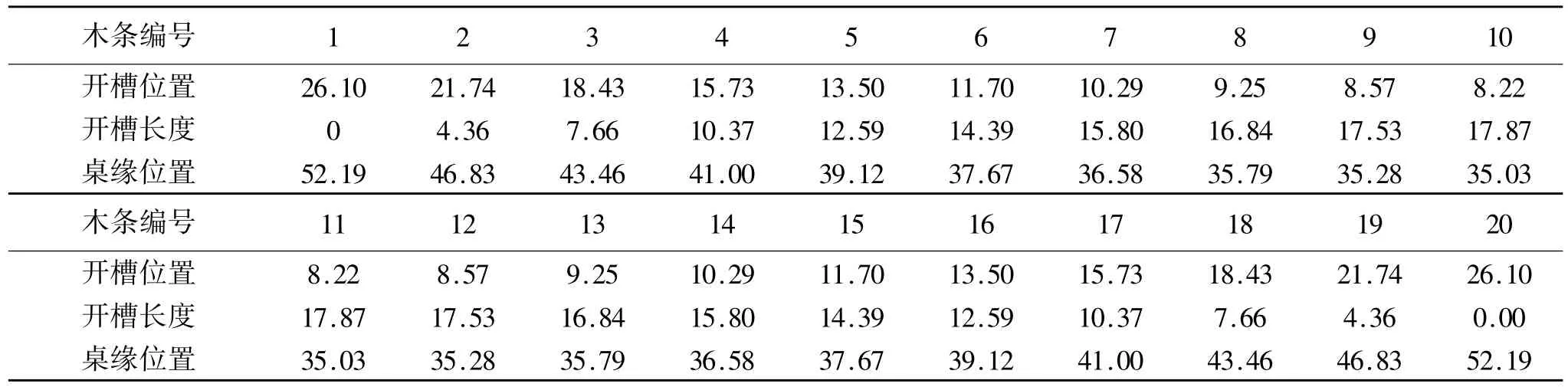
表1 开槽长度、位置及桌缘切割位置(单位:cm)
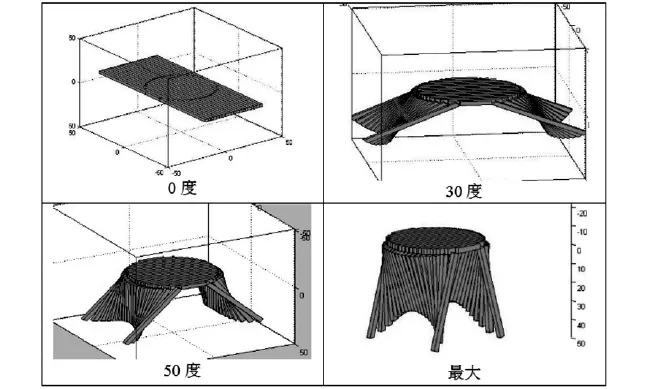
图3 折叠桌动态变化过程示意图
求得折叠桌的动态变化过程如图3所示.
并用Matlab拟合[6]可求出桌脚边缘线的数学描述为:
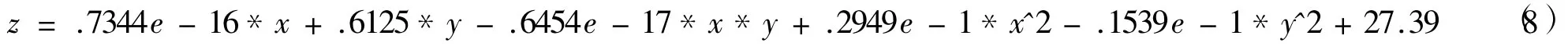
其图形如图4所示.
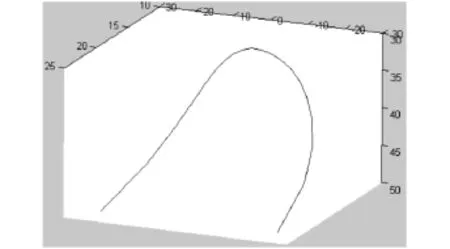
图4 桌脚边缘线拟合结果示意图
4.2 圆形折叠桌的优化设计建模与求解
4.2.1 优化设计建模
问题二优化模型的建立主要从稳固性、加工便利性、耗材等方面考虑:
1)考虑稳固性
由问题分析可知,取两脚外缘边距离为桌面宽度,使得下边四脚位于正方形的四个顶点上,此时最稳固且不占空间,所以有:
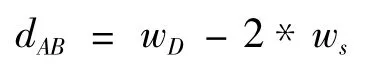

如图2所示,减2*ws是因为wD包括两脚木方的厚度,从而确保四脚处于完全的正方形.
2)考虑加工便利性
即要使得槽长lg尽可能小,设η为钢筋分桌脚的位置,,如η=0.3时,即钢筋分脚下边的长度lp=0.3 lf,由、有:

3)考虑耗材最少
也即要使得lD达到最少:
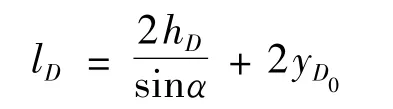
但若确定了稳固性,lD可由式求出.
4.2.2 优化设计求解
对于桌高70 cm、桌面直径80 cm的情形,利用式-可以求解得到最优设计加工参数,我们解得的最优方案是四边桌脚呈正方形且相距80 cm时为最优,此时解得平板长度为:
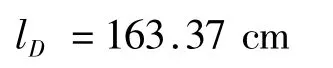
则平板尺寸为:163.37×80×3 cm
钢筋位置为:距平板两端29.3 cm
开槽长度、位置及桌缘切割位置如表2所示.

表2 开槽长度、位置及桌缘切割位置(单位:cm)
4.3 任意创意折叠桌的建模与求解
4.3.1 创意折叠桌的建模
实际上,对于任意设定折叠桌高度在4.1、4.2节中的模型即可解决,而对于任意桌面边缘线只需要把半径r替换成相关的曲线方程,利用微分即可求出桌面边缘为任意曲线的折叠桌,并可利用Matlab软件仿真出真实折叠桌,我们设计的仿真部分程序如第5部分所示.
4.3.2 创意折叠桌的求解
利用我们建立的创意折叠桌模型对客户要求的椭圆桌进行建模计算可得到加工参数如表3所示,并可模拟得如图5所示的仿真结果.
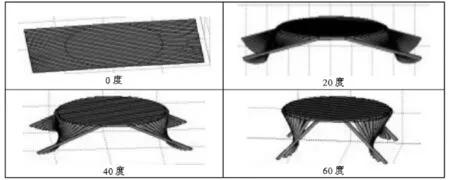
图5 客户设计的椭圆桌仿真图
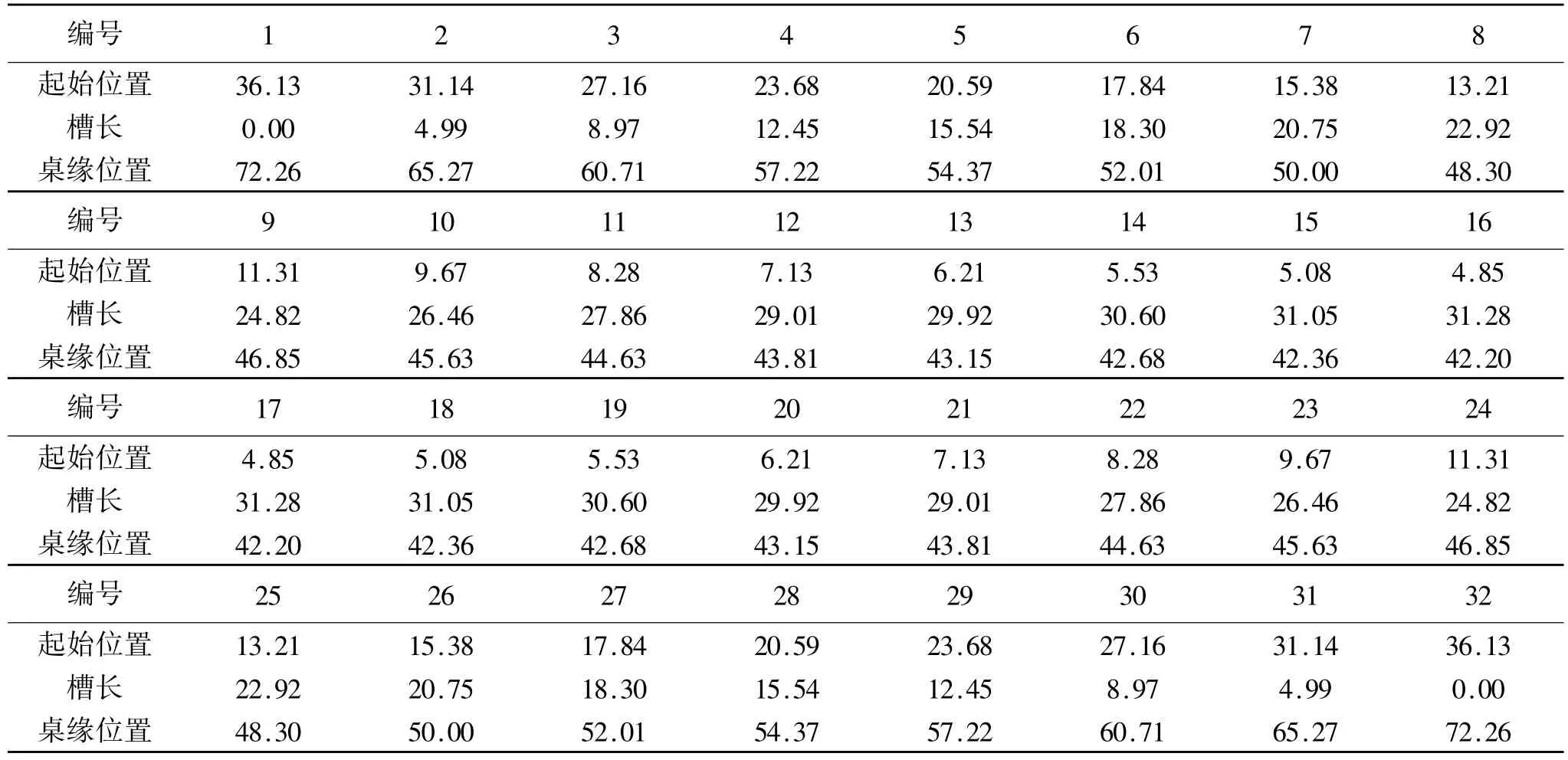
表3 客户设计平板桌开槽长度、位置及桌缘切割位置(单位:cm)
5 模型的仿真
为方便读者进行类似研究,本文给出桌腿位置参数计算及绘制关键Matlab[6]代码.


6 结束语
为了解决创意折叠桌的优化设计问题,本文首先从简单常用的圆形折叠桌出发探讨折叠桌脚动态变化的模型建立,通过使用微元法将桌脚直纹曲面的变化巧妙的转换成每个脚独立的桌脚面离散变化模型,该模型简单易行,便于用Matlab编程仿真实现和求解,故对于给定的桌高和板材长度我们可以轻易求出该桌子的加工参数,并对该加工参数分析了优化设计方案.分析中发现只要用户能给出桌面边缘的曲线方程,我们即可利用圆形折叠桌的加工参数求法计算出任意用户指定的折叠桌的加工参数.并在最后给出了该折叠桌的仿真代码,方便了创意折叠桌的自动化设计和生产.但该模型假设桌子撑起后以铰链固定,省略了受力分析,实际情况中受各种因素的限制和影响,该模型的假设不一定成立,这将是我们下一步工作.
[1]韩佳成,Robert Van Embricqs.平板折叠边桌[J].设计,2012(8):24.
[2]蔡国梁,李玉秀,王世环.直纹曲面的性质及其在工程中的应用[J].数学的实践与认识,2008,38(8):100-102.
[3]侍冰雪,朱家明,朱韶东,等.创意平板折叠桌优化设计方案[J].浙江科技学院学报,2014:26(6):429-435.
[4]刘睿,张蒙,张政.创意平板折叠桌优化设计[J].西安航空学院学报,2015,33(3):65-71.
[5]赵洪斌,吴知丰,谢礼立.自锁式平板折叠网架折展过程参数设计[J].哈尔滨工业大学学报,2007,39(8):1202-1204.
[6]胡守信,李柏年.基于MATLAB的数学实验[D].北京:科学出版社,2005.
Modeling and Analysis of the Creative Rising Side Table
SUN Fa-jun,ZHANGMeng,DU Yue-hao,ZENG Liang-ru
(College ofMathematic and Computing Science,Huaihua University,Huaihua,Hunan 418008)
In order to solve the automatic design of a kind of creative folding table in the presentmarket,the modeling of simple circular folding table is discussed at first.Dynamic change of folding table legs ismodeled as the relationship between the desktop and the angle of the table foot with differentialmethod,with which the processing parameters such as the position and length of the round table can be obtained.Then the optimization design of processing parameters is discussed from the aspects of stability,processing convenience,material and so on.The analysis shows that a set of optimization parameters with stability,consumablesand industrial processing can be calculated for an arbitrary creative folding table as long as the user provides the desktop edge curve of its.And then the modeling and calculation of the elliptical folding table with the height and width are discussed.At last,the simulation of the folding table is analyzed,and the key simulation codes are suggested.
rising side table;optimization model;processing parameter;simulating in Matlab
O242.1
A
1671-9743(2015)11-0024-07
2015-09-24
怀化学院科研项目(HHUY2013-02);湖南省教育厅教改项目(湘教通[2014]247号-465);怀化学院重点教改项目(2014-13).
孙发军,1976年生,男,讲师,研究方向:算法与并行计算、无线传感器网络.

