农用高压电网圆柱形殷钢电容分压器边缘效应的研究

董赫，李伟凯

（黑龙江八一农垦大学信息技术学院，大庆 163319）

农用高压电网圆柱形殷钢电容分压器边缘效应的研究

董赫，李伟凯

（黑龙江八一农垦大学信息技术学院，大庆 163319）

通过殷钢电容分压器理论计算值与实际测量值的对比，得到边缘效应的存在导致电容分压器的实际测量值偏大的结论。以理论分析为切入点，结合微积分原理及电容串联思想，推导出计及边缘效应的分压器电容值计算公式。针对圆柱形电容器的特点，提出利用增加电容分压器边缘电容环倒角半径的方法来削弱边缘效应，并通过试验验证了该方案的可行性。

农村电网；圆柱形殷钢电容分压器；边缘效应；圆环倒角

随着我国农网改造升级进程的加快，农村高压电网的检测和监测也越来越被国内外电气学者以及电力研发机构所重视[1]。电压互感器作为农村电网中不可或缺的监测元件，其监测的稳定性和测量的精确度直接影响整个电网线路的正常运行。在农村电力系统中，电压互感器实际上是一台微型变压器；通过其内部的高压电容分压器分压，将低电压传导在精密测量元件上（电压约3～5 kV）[2]。作为电容分压型电压互感器的核心部分，只有使高压电容分压器实时处于精确、稳定的工作状态，才能确保整个农村电力系统检测、监测正常运行。

圆柱形同轴殷钢高压电容分压器结构示意图如图1所示。殷钢作为一种高稳定度、低膨胀系数的合金材料，现已经被广泛应用于武器制造及精密仪器等行业。殷钢制成的高压电容分压器因其膨胀系数小、稳定度高的优秀性能，成功地解决了传统电容分压器温度漂移、分压能力低等问题。但是受现代工艺技术的限制，殷钢的制造成本较高、合成度较低、造价昂贵；这些原因极大的限制了殷钢在电气领域中的应用前景[3]。通过对比同一殷钢电容分压器的理论计算值与实际测量值，得出其实际测量值偏大且误差高于10%的结论。进而以殷钢电容分压器理论分析为切入点，结合微积分原理与电容串联思想，推导出计及边缘效应的圆柱形电容器电容值一般计算公式；最后基于圆柱形电容分压器的特殊性，提出利用增大电容器边缘电容圆环倒角半径的方法削弱其边缘效应，并通过试验验证了该方案的可行性。研究的方法与结论，为深入研究农用高压电网殷钢电容分压器的相关特性提供了一定的理论依据。

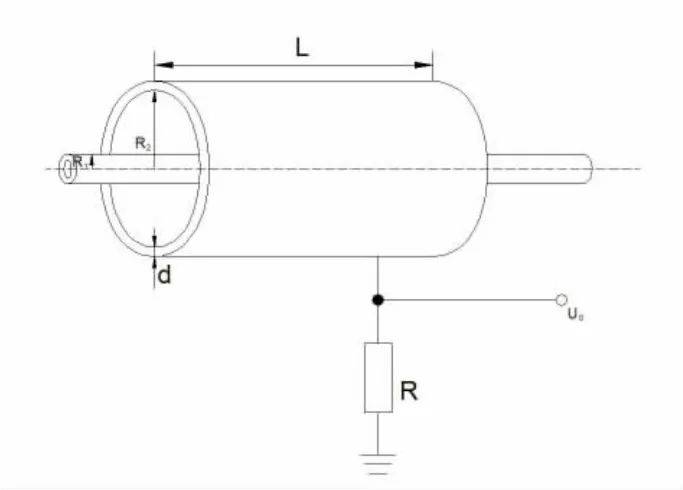
图1 殷钢电容分压器示意图Fig.1Schematic invar of capacitive divider

1 殷钢电容分压器理论值计算

基于殷钢的同轴圆柱形电容分压器等效电路如图2所示。工作状态下将高压电极和低压电极分别接在电容分压器的内、外圆柱上，圆柱筒内介质为空气，半径R1=22.9 mm，R2=62.2 mm，圆柱同行部分的电容器长L=900 mm。同轴圆柱形殷钢电容分压器的其他常规参数如表1所示。

图2 殷钢电容分压器等效电路图Fig.2Invar equivalent circuit of capacitive divider

表1 殷钢高压电容分压器常规参数表Table 1Divider parameter table of invar on high voltage capacitor

文献[4-5]中给出的圆柱形电容分压器电容计算式为：

式中ε0是介电常数，取8.854×10-12；εr为空气的介电常数，取1.002。这也是忽略边缘效应时圆柱形电容器电容值的计算式；所以忽略边缘效应上述殷钢电容分压器电容的理论计算值为：

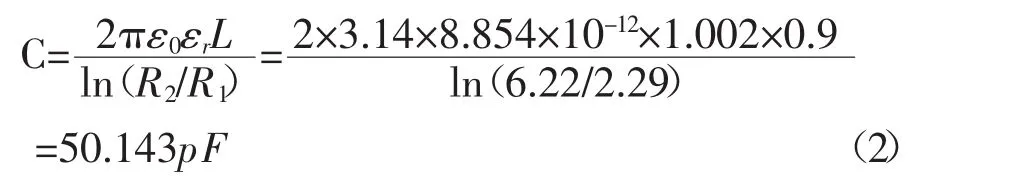
为了获得殷钢电容分压器工作状态下的电容标准值，采用自动抗干扰精密介质损耗测量仪AI-6000对其实际电容值进行测量。条件为：室温（20℃）、频率50.00 Hz、电压由0.5 kV逐渐增至10 kV。测得分压器实际电容值如表2所示。

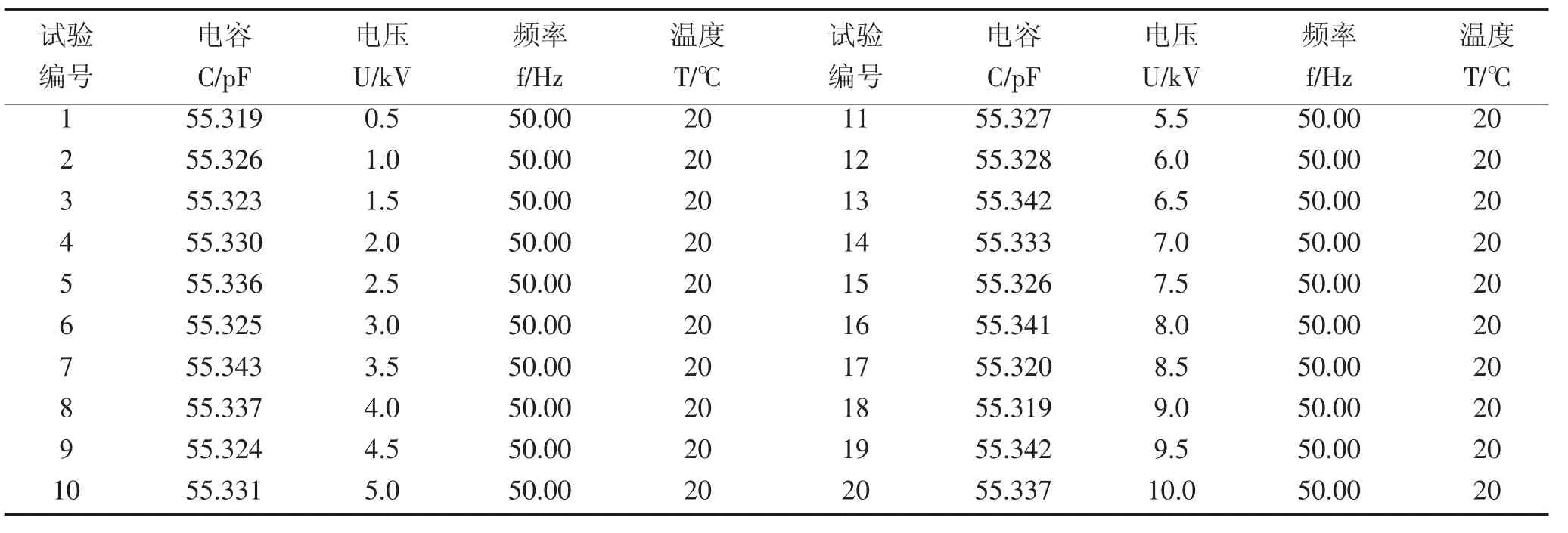
表2 殷钢（空气）20℃0.5～10 kV耐压数据Table 2Pressure data of invar（air）on 20℃0.5-10 kV

表2中圆柱形殷钢电容分压器实际测量值的平均值C1为55.331，所以分压器工作状态下的电容值误差δ为

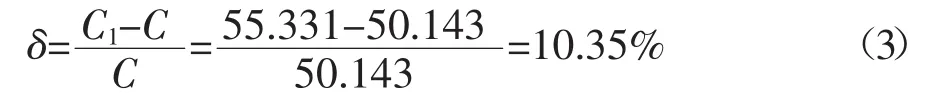
根据公式（3）可知，分压器工作状态下的电容实际测量值大于其理论计算值，并且误差超过10%。深入分析可知，因为边缘效应的存在使得电容分压器实际电容值与“忽略边缘效应”的理论计算值呈现差异。此种由边缘效应引发的分压器电容值增加，导致农村电网中其他元件监测精度降低的现象，从根本上限制了电容分压型电压互感器在电力系统中的应用前景。因此深入研究电容分压器的边缘效应，必将为电容分压型电压互感器的应用前景带来新的契机。

2 圆柱形殷钢高压电容分压器边缘效应的理论分析

圆柱形电容器的边缘效应是指：工作状态下，电容器边缘部分及外表面部分的电荷量与中间部分电荷量分布不均，导致边缘电场与电容器内部电场差异，这类电场差异产生的效应称之为圆柱形电容器的边缘效应[6]。任何形状的电容器工作状态下都存在边缘效应，有些学者应用物理学和高等数学的方式对非理想边缘平行板类电容器电容进行过深入解析；得到的结论是，只有当平行板类电容器极板宽度与极板间距之比大于16.644时，才能将电容器理论计算值与实际测量值之间的误差控制在10%以内[7]。由此易见，边缘效应对农村电力系统中精密电容器造成的影响是极其严重的。

为了使推导出的电容计算公式不失一般性，选取任意尺寸的同轴圆柱形殷钢电容分压器为研究对象（两圆柱之间介质为空气）。分压器的内、外极板半径分别为R1、R2，同轴平行长度为L，圆心角为θ。根据对称性，只需研究一个侧面即可同理推出另一个侧面。设Q1为圆柱中间极板正对面所带电荷量的绝对值，Q2为两端极板边缘以及其他部分所带电荷总量的绝对值。所以分压器的电荷总量可表示为：

根据电容的定义：

令ρ1为正对面积所带的电荷密度，所以：

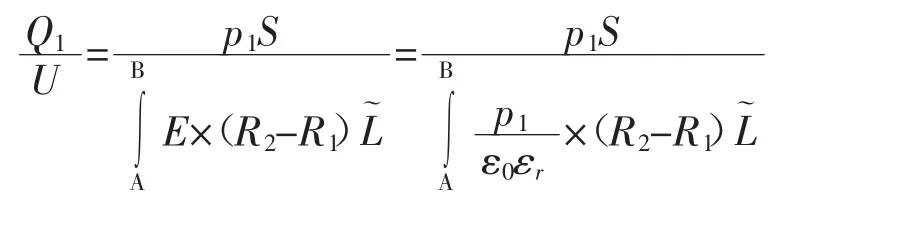
公式（6）中，S表示圆柱形电容器极板正对部分面积的一半，因此：

带入（6）得：

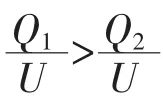
结合微积分思想及电容串联定义寻求电容器计算公式的方法，既简捷又不是一般性，计算结果可直接应用。依据微积分思想，可以将整个圆柱形电容分压器看成是由多个微小电容器串联而成，再利用电容串联的定义进行累加，最终推导出电容分压器电容值的精确计算公式。

在圆柱形电容器两极板间任意位置，截取一个半径为r、圆心角为θ、高度为L的圆柱面。此柱面与其极间距离为dr的同心同高柱面构成一个微电容器。因为dr无限小，所以此微电容器可视为平行板电容器，电容大小为：

此时所有电容可视为由无限个上述微电容器串联而成，所以总电容为：

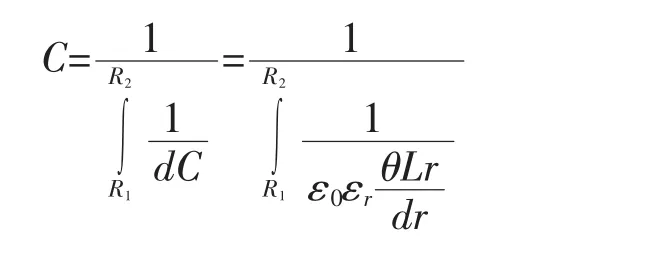
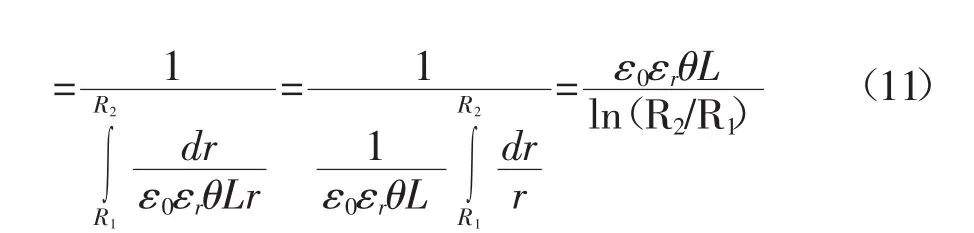
进而推导出的计及边缘效应的圆柱形电容器电容计算公式为：

由公式（12）可知，当且仅当θ=2π时，即电容分压器为理想状态的情况下，理论计算值与实际测量值等同。推导出的公式（12）适用于圆柱形电容分压器计及边缘效应时的电容值计算，具有一般性和通用性。

3 利用增大电容器边缘圆环倒角半径削弱边缘效应的影响

无论是规则的平行板类电容器还是同轴圆柱类电容器，其边缘效应在实际应用中都不可避免更不能忽略。如何削弱甚至消除电容分压器边缘效应带来的影响，一直都是各国电气制造商以及电气学者们研究的关键点。针对平行板电容器，若想要削弱其边缘效应，只能在增加极板间宽度的同时尽量减小上下极板的间距[9-10]。然而缩短上下极板间距的代价是更改电容分压器的电容值；如果单一的无限制增加电容分压器极板宽度，又会衍生出制造成本过高、分压器自重过大等一系列新问题，在实际应用中势必会造成许多不必要的浪费，这也是平行板类电容器在农村高压电力系统中应用受限的根本原因。

针对圆柱形电容分压器的特点，依据公式（9）和（12）的理论分析，以及考虑到圆柱形电容环尺寸受Plug And Switch System制约等因素；提出利用增加圆柱形电容分压器边缘倒角半径的方法来抑制边缘效应的方案，具有一定的可行性和实际意义。为了验证该方案的正确性，分别对电容器边缘电容环倒角半径r为0.5 mm、1.5 mm和3.0 mm的电容分压器，在室温（20℃）条件进行0.5～10 kV电容值测试试验，结果如表3、4、5所示。

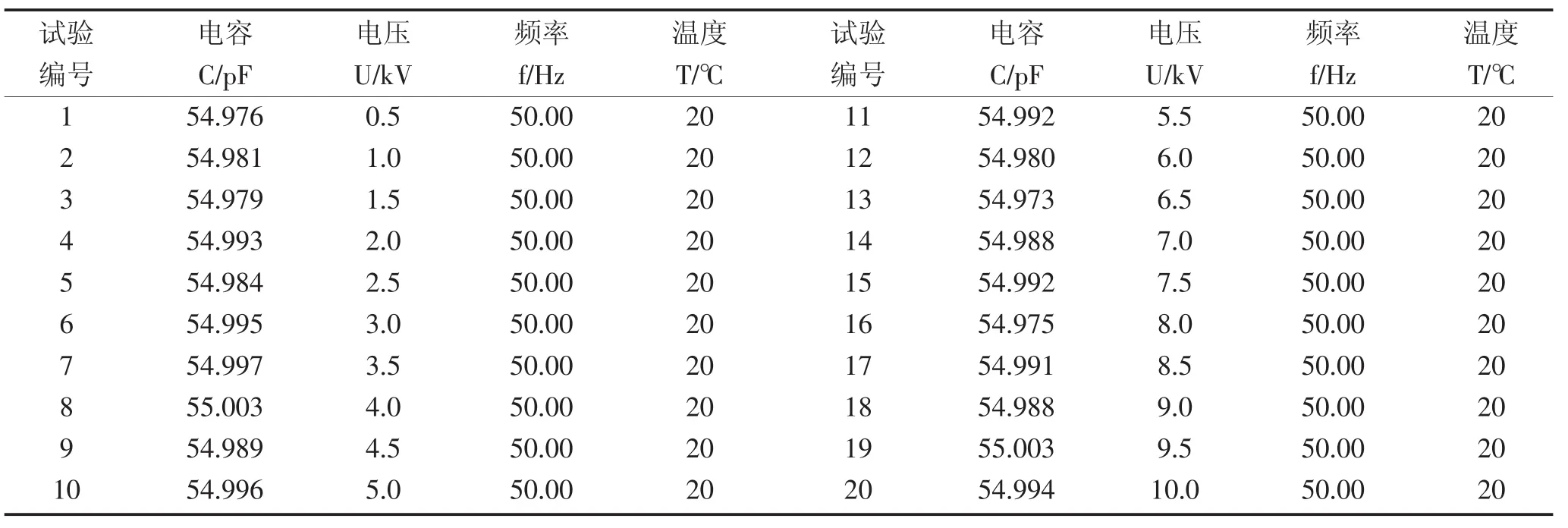
表3 倒角半径r=0.5 mm殷钢（空气）电容分压器电容测量值Table 3Capacitance measurements of capacitive divider on fillet radius r=0.5 mm Invar（air）

表4 倒角半径r=1.5 mm殷钢（空气）电容分压器电容测量值Table 4Capacitance measurements of capacitive divider on fillet radius r=1.5 mm Invar（air）

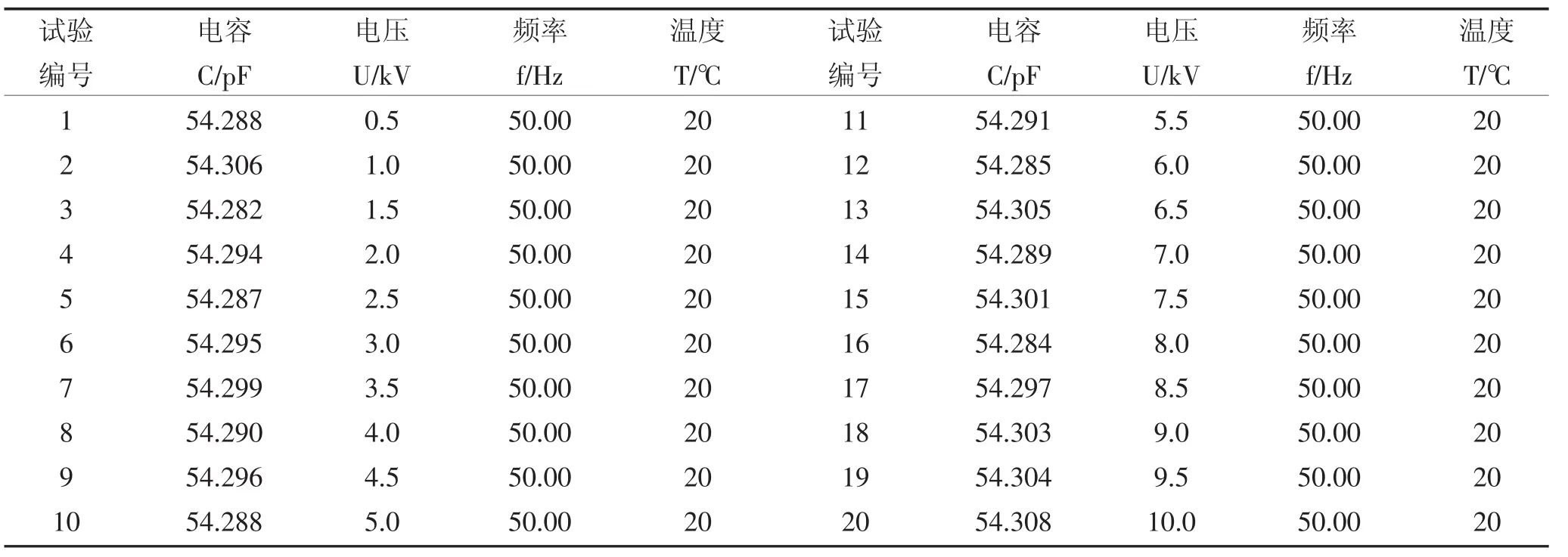
表5 倒角半径r=3.0 mm殷钢（空气）电容分压器电容测量值Table 5Capacitance measurements of capacitive divider on chamfer radius r=3.0 mm Invar（air）

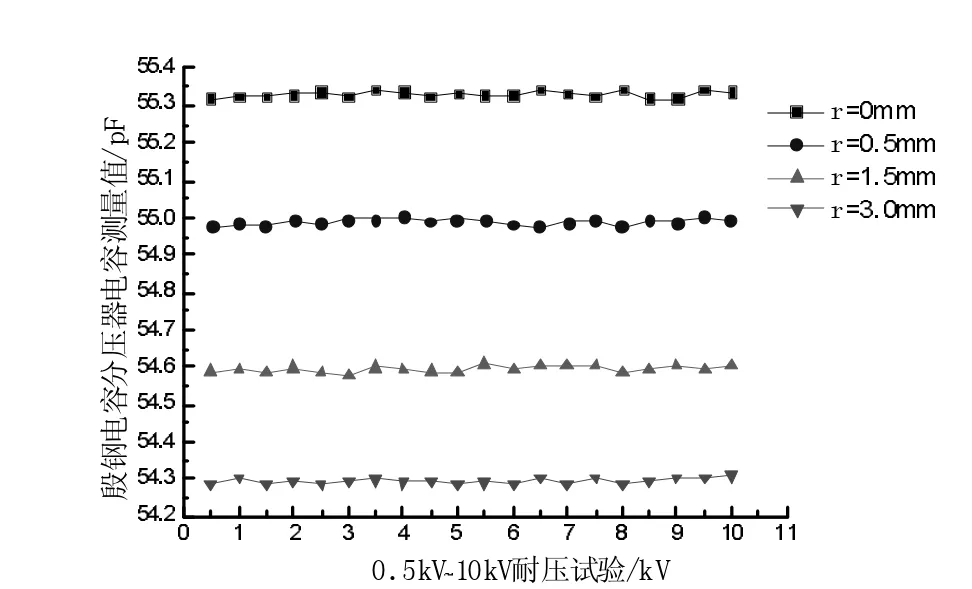
图3 倒角半径r与电容分压器电容测量值关系Fig.3Capacitance measurement values of fillet radius r and capacitive voltage divider

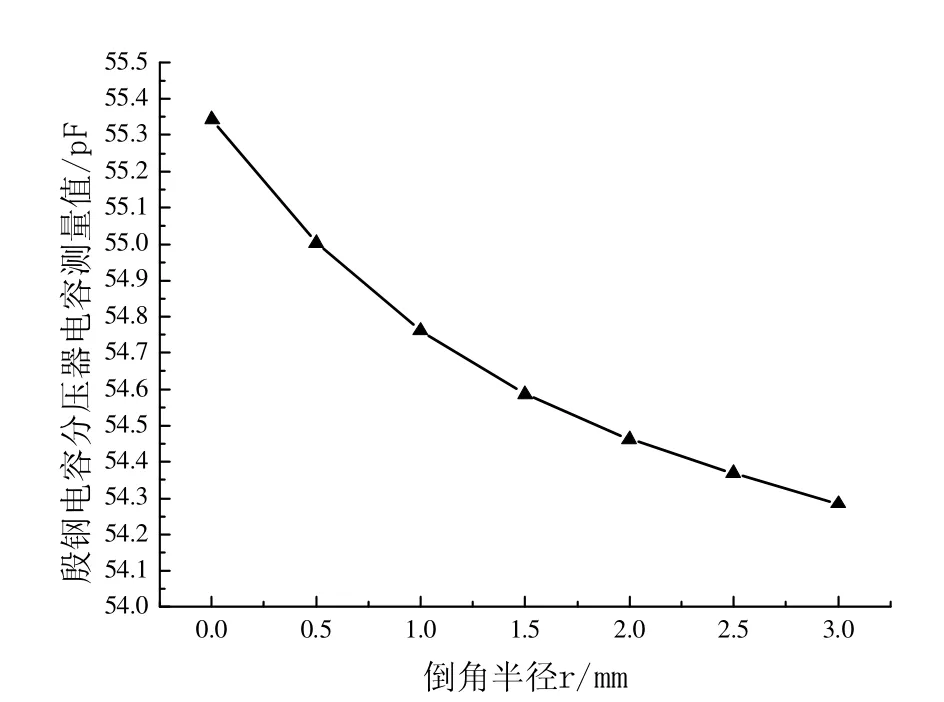
图4 倒角半径r与电容分压器实际电容值关系图Fig.4Actual capacitance value graph of fillet radius r with capacitive divider

通过分析上述试验结果，可以发现采取增加电容器边缘电容环倒角半径的方法，的确在一定程度上削弱了分压器的边缘效应。结合图3、4能够清晰、直观的得出，电容分压器的电容测量值与边缘电容环倒角半径成反比，即电容器的电容测量值随边缘电容环倒角半径的增大而减小，二者近似线性相关；所以在倒角半径无穷大的情况下，可以认为电容分压器电容的理论计算值与实际测量值相等。

不过值得深思的是，当利用现代工艺对殷钢高压电容分压器边缘电容环进行倒角处理时，势必会人为降低电容分压器边缘部分的物理厚度，边缘变薄又会导致电容分压器边缘击穿的概率增加。所以探究并找出殷钢电容分压器边缘效应与边缘击穿现象之间的平衡点，是深入研究如何提高农用高压电网殷钢高压电容分压器测量精度、运行稳定行等相关特性较为实际的切入点。

4 结论

（1）通过圆柱形殷钢电容分压器理论计算值与实际测量值的对比，得出二者之间误差超过10%。说明分压器因边缘效应产生的影响不可忽略。

（2）以理论分析为切入点，结合微积分原理及电容串联思想，推导出计及边缘效应的圆柱形电容分压器电容值计算公式，此公式具有一般性和通用性。

（3）基于圆柱形电容器的特点，提出利用增加电容器边缘电容环倒角半径的方法削弱边缘效应，并通过试验验证了此方案的可行性，为深入研究农用高压电网圆柱形殷钢电容分压器的相关特性提供了一定的理论依据。

［1］宋征亮.发展农村智能电网的意义、特点和可行性分析［J］.技术应用，2012，13（6）：24-26.［2］康忠伟，石莉莉，孙艳波.抽水电机组技能控制装置的研究与设计［J］.黑龙江八一农垦大学学报，2013，25（6）：74-77.

［3］陈昀，李明光，张艳红，等.因瓦合金发展现状及应用前景［J］.机械研究与应用，2009，22（4）：9-11.

［4］李伟凯，郑绳楦.高压电压互感器精密电容分压器的研究与设计［J］.传感技术学报，2005，18（3）：634-637.

［5］葛松华，唐亚明.用电容器的电阻和电容特性公式计算非平行板电容器的电容［J］.物理通报，2012，21（7）：35-36.

［6］蒋泽，杜惠平.任意尺寸圆柱电容器电容的计算［J］.电子测量与仪器学报，2005，19（2）：49-50.

［7］朱益清，徐坚宏.计及边缘效应的平行板电容器的电容计算［J］.工科物理，1998，8（1）：6-9.

［8］D Gilbarg.A Generalization of Schwarz-Christoffel Transformation［J］.PNAS，2006，6（2）：36-41.

［9］谷长寿，张颖，曹立生.平行板电容器边缘效应的研究［J］.辽宁工学院学报，1994，3（14）：80-82.

［10］邱万英.非理想边缘电容器电容的分析［J］.华东交通大学学报，2008，25（3）：86-89.

Application Study of Agricultural High-voltage Grid of Cylindrical Invar on Capacitive Divider Edge Effects

Dong He，Li Weikai
（College of Information and Technology，Heilongjiang Bayi Agricultural University，Daqing 163319）

By comparing the calculated value and actual measurement value of invar on the capacitive voltage divider，the presence of edge effects caused the actual results was too large capacitive divider conclusions.The theoretical analysis was used as a starting point and combined with calculus theory and capacitors idea，and the edge effects formula of the total capacitance value was derived. According to the characteristics of the cylindrical capacitor，the approach of increasing the capacitive divider edge capacitance on the ring chamfer radius was provided to weaken the edge effect，and the test had been passed to verify the program feasibility.

agricultural high-voltage grid；invar cylindrical capacitive divider；edge effects；ring chamfer

TM615

A

1002-2090（2015）02-0092-05

10.3969/j.issn.1002-2090.2015.02.021

2014-06-06

董赫（1988-），男，黑龙江八一农垦大学信息技术学院2012级硕士研究生。

李伟凯，男，教授，博士研究生导师，E-mail：bynd@263.net.cn。