航磁异常深部弱信号提取技术研究
郭志馗,张青杉,陈 超, 戴继舒,陈海弟,孙 凯,王秋革
(1. 中国冶金地质总局地球物理勘查院,河北保定 071000;2. 中国地质大学(武汉)地球物理与空间信息学院,地球内部多尺度成像湖北省重点实验室,湖北武汉 430074)
航磁异常深部弱信号提取技术研究
郭志馗1,2,张青杉1, 2,陈 超2, 戴继舒1,陈海弟1,孙 凯2,王秋革2
(1. 中国冶金地质总局地球物理勘查院,河北保定 071000;2. 中国地质大学(武汉)地球物理与空间信息学院,地球内部多尺度成像湖北省重点实验室,湖北武汉 430074)
磁异常通常是地下不同深度磁性地质体产生磁场的叠加,在规范高度的航磁测量结果中,深部磁性体所产生的异常通常表现为弱而平缓,其水平与垂向分辨率均较低,在航磁资料处理解释中难以有效捕获。因此,应用适当方法提取由深部地质体引起的弱磁信息是十分必要的。本文采用精度高且稳定的位场延拓技术将航磁异常向下延拓,可以稳定增强磁异常幅度,随着延拓面与场源之间距离的减小,浅成磁信号与深成磁信号的视深度差异将增大,在对数功率谱上可以将其区分,而后可利用匹配滤波方法将浅部信号剥离,从而得到深部弱信号,同时可计算深部弱信号的视深度。
深部弱信号 向下延拓 匹配滤波 频谱分析
Guo Zhi-kui , Zhang Qing-shan, Chen Chao, Dai Ji-shu, Chen Hai-di, Sun Kai, Wang Qiu-ge. Extracting weak magnetic signals at depth from aeromagnetic anomaly data [J]. Geology and Exploration, 2015, 51(6):1007-1015.
0 引言
21世纪以来,攻深扫盲已成为我国矿产勘查的重要目标,利用磁测技术勘探磁性盲矿体是一种行之有效的方法,高精度磁测可在区域普查以及深部找矿中发挥作用(曹新志等, 2009),但由于深部磁性矿体在地面或空中引起的磁场变化幅度相对较小,为了更好地挖掘深部地质信息,研究深部弱磁信号提取方法是必要的。
传统磁法勘探处理解释技术中,将小于2.5倍异常总精度的异常信息视为不可靠异常,其通常不被重视(刘云祥, 2007)。弱磁异常往往被忽略,致使勘探效果受到影响,依据磁测数据质量研究弱磁异常的提取处理新技术,有助于提高磁法勘探解决地质问题的能力(管志宁等,2002)。
位场向下延拓是突出浅部异常的有效方法,在“放大”浅部异常的同时,深部异常信号也会得到一定程度的增强。近年来,稳定位场向下延拓方法发展迅速,如迭代Tikhonov正则化方法(Zengetal., 2013)、迭代泰勒级数(Zhangetal., 2013)法以及改进的迭代维纳滤波方法(曾小牛等, 2014)等,延拓稳定性和精度都有很大提高(Lietal., 2009;卞光浪等, 2014),延拓深度更大。借助高精度稳定下延方法,使得航磁异常中的深部弱信号提取成为了可能。刘天佑等(2006)利用小波多尺度分解提取深部弱信号应用于危机矿山挖潜,Xuetal.(2009)将小波多尺度分解与频谱分析结合分离位场异常,给出分离后的位场视深度信息。本文使用改进的Tikhonov正则化向下延拓方法增强深部弱信号,增大深部信号与浅部信号的视深度差异,并结合等效层思想(Pawlowski, 1994),将下延后的数据进行匹配滤波剥离浅部信号从而得到深部信号,并给出深部弱信号的视深度。
1 方法原理
1.1 改进的正则化向下延拓
位场向下延拓是向上延拓的反问题,在空间域用第一类Fredholm积分方程表示:
(1)
其中u0(x,y)和uh(ξ,η)分别表示观测面和延拓面上的场值,h为延拓深度,如图1所示。

图1 位场向下延拓示意图Fig.1 Schematic diagram of downward continuation of potential field
采用与杨文采(1986)同样的方式,将延拓积分方程(1)离散化为线性方程组:
GUh=U0
(2)
其中G是延拓核矩阵,具有平移等效性和互换对称性,其它元素均可由第一行元素换算得到(陈龙伟,2012):
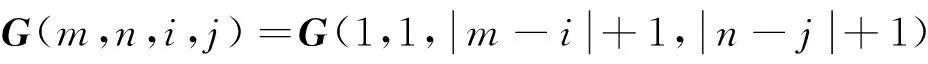
Uh和U0分别是延拓面和观测面上的位场数据构成的列向量:
对于方程(2)可以采用奇异值分解(Singular Value Decomposition)算法(Xu, 1998;郭成豹等, 2008)求解。当向下延拓深度较大时,G会出现小的奇异值,如图2所示,因观测数据通常都含有噪声,这些小的奇异值会放大噪声,造成下延解的不稳定。对于这种不适定问题,Tikhonov正则化是行之有效的方法(梁锦文,1989;曾小牛等, 2011),但常规正则化参数μ是大于零的常数,在压制噪声的同时也对数据的可靠部分进行了压制,本文结合截断奇异值分解方法(Truncated Singular Value Decomposition)引入一个正则化矩阵Lμ(Fuhryetal., 2012),只对小奇异值(不可靠部分)进行修正,大奇异值(可靠部分)保持不变,以增强向下延拓的稳定性及保幅性,向下延拓的解可以表示为:
(3)
其中,U,Σ,V是G的奇异值分解矩阵
(4)
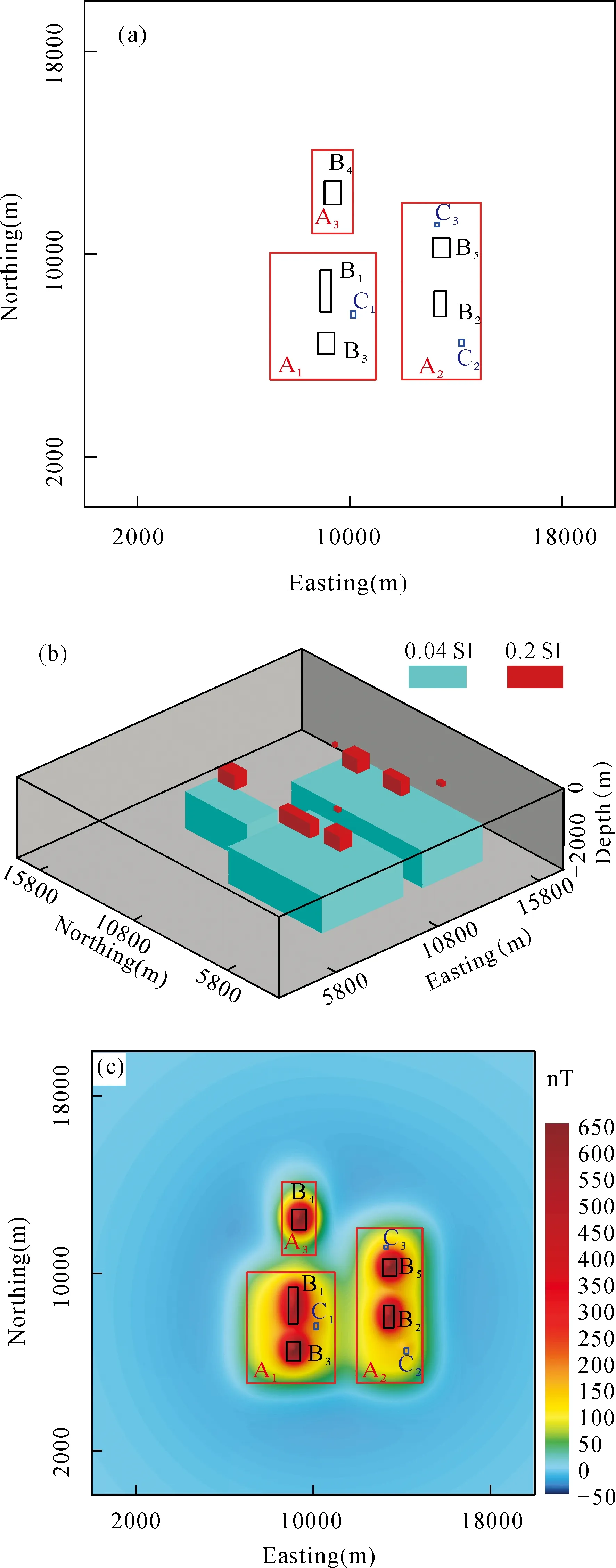
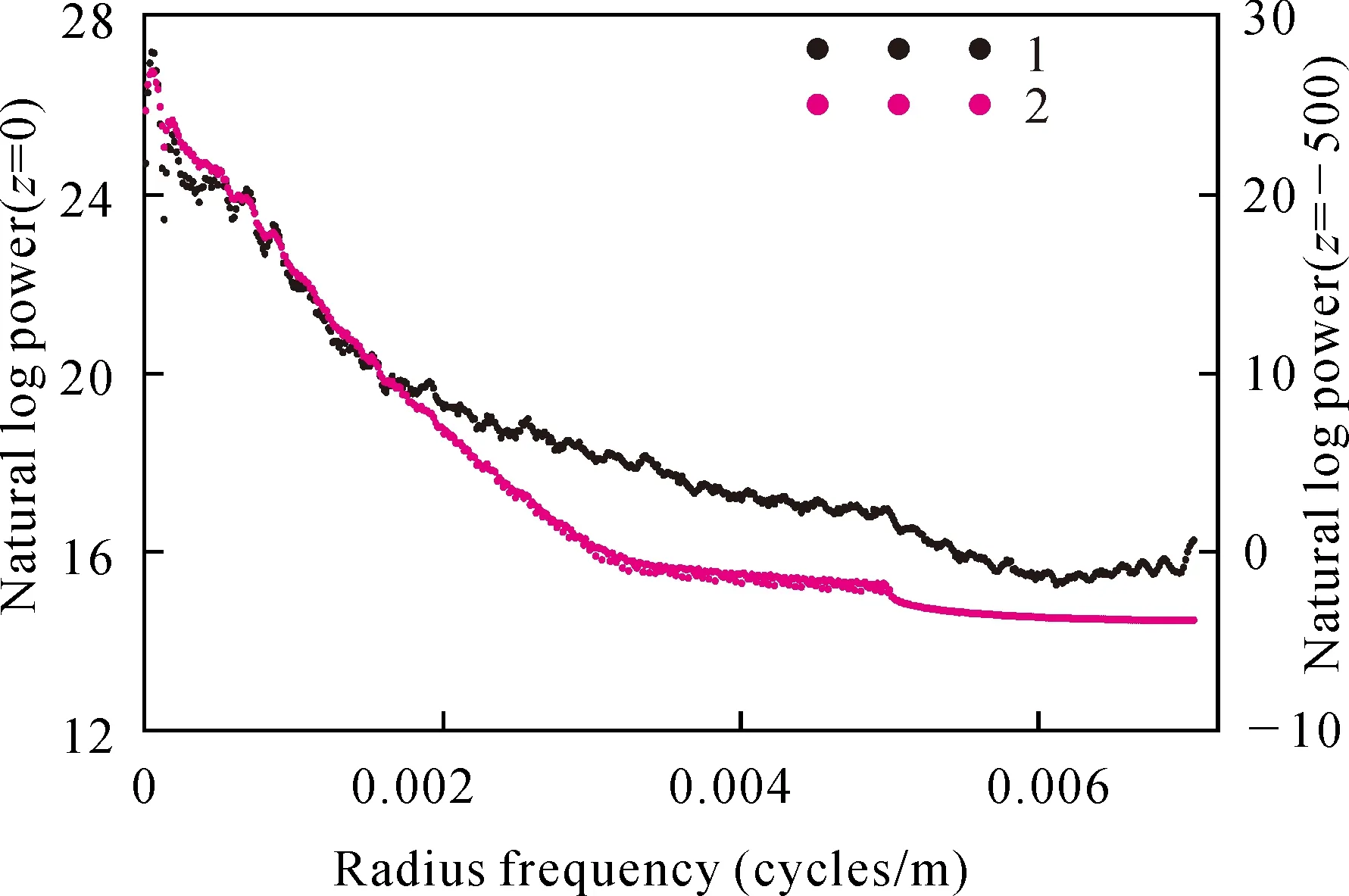
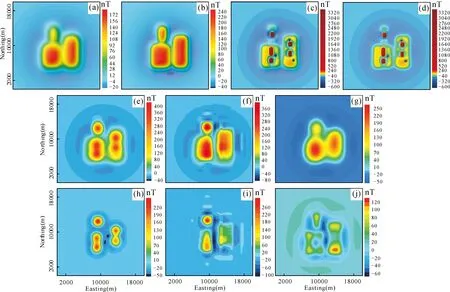
其中σi(i=1, 2, 3,…,n)是G的奇异值,μ>0是正则化参数,0 图2 下延核矩阵奇异值随延拓高度的变化Fig. 2 Kernel matrix singular values changing with centinuation heights 对于改进的正则化向下延拓方法,其关键是确定合适的正则化参数μ和截断参数k,目前已有较多可行方法,比如广义交互确认法(Generalized Cross-validation, GCV)和L-曲线法(Lietal, 2003)等,本文使用L曲线法(在此不赘述)。 下面对改进的正则化下延因子的滤波特性做简要探讨,为方便起见,在频率域讨论其滤波特性。对(3)式两边取傅里叶变换,得到改进的正则化下延在波数域的延拓算子: (5) 不同下延方法滤波函数频率响应曲线对比如图3所示,改进的正则化下延因子对截断频率以下的低频段无压制,大于截断频率时与常规Tikhonov正则化方法一致。 图3 不同下延方法滤波函数频率响应曲线Fig. 3 Frequency response curves of filter function with different downward continuation methods1-Tikhonov正则化方法;2-迭代Tikhonov正则化法;3-Land- weber迭代法;4-积分迭代法;5-改进的正则化方法1-Tikhonov method; 2-iterative Tikhonov method; 3-Landweber iteration method; 4-integral iteration method; 5-improved regulariza- tion method 为检验改进的下延方法效果,采用理论模型比对方式,模型为两个垂向磁化水平圆柱体,半径分别为500 m和400 m,中心埋深均为550 m,圆柱中心水平位置分别为3000和6000,磁化率均为0.2 SI,地磁场大小取50000 nT,正演计算地面之上200 m的ΔT,并加入最大振幅为15 nT的随机噪声以模拟观测磁异常。 图4 向下延拓模型试验Fig. 4 Downward continuation of synthetic magnetic dataa-L曲线;b-理论曲线及下延至地面曲线;1-Tikhonov正则化方法,μ=0.0104;2-改进的正则化方法;3-地面上理论计算磁异常;4-地面之上200m含噪声理论磁异常;5-Tik- honov正则化方法,μ=0.094a-L-curve of improved method;b-downward continuation result;1-Tikhonov method, μ=0.0104; 2-proposed improved method; 3-theoretical data at z=0m; 4-noisy synthetic data simulated from two horizontal cylinder at z=-200m; 5-Tik- honov method, μ =0.094 采用常规Tikhonov正则化方法和改进的正则化方法将模拟观测磁异常下延200 m,利用L-曲线法确定最佳Tikhonov正则化参数μ=0.0104,如图4(a)所示;对于改进的正则化方法,为了更好地压制噪声,正则化参数取值稍大(这里取为μ的9倍);截断参数取为与正则化参数最接近的奇异值对应的序号k=30;下延结果如图4(b)所示。从下延磁异常曲线看,改进的向下延拓因子对高频噪声压制较好,对低频部分未予过多压制,保幅性更好。若常规Tikhonov正则化方法正则化参数增大(取为μ=0.094),则下延曲线中噪声明显减小,但异常幅值被相应压制。也就是说,常规Tikhonov正则化方法若想使低频部分更保值,则必然放大更多高频噪声。通过计算下延结果与理论值的均方误差,可以定量评价两种方法的下延效果,常规正则化方法下延结果与理论值之间的相对误差分别为10.1%和5.3%,而改进方法为3.8%。 1.2 匹配滤波分离垂向位场 位场信号的径向平均对数振幅谱(功率谱)曲线,可拟合为n条不同斜率的直线段,直线斜率即为 不同场源等效层深度(公式推导不再赘述,参见参考文献,刘青松等, 1996)。 磁异常功率谱可简化表示为(Syberg, 1972): (4) 其中,E、A为常量,k为径向波数,h为等效层深度,Wj(k)为第j个等效层的匹配滤波因子,可由下式计算: (5) 继而可由(4)式的后半部分计算第j个等效层的功率谱,进而变换求取该等效层的磁异常。 当不同磁性体垂向相对接近时,在对数振幅谱上将难以明确区分,经下延处理后,可视作观测面下移,磁性体垂向距离相对变大,其对数振幅谱发生变化并可区分,以此类推,利用匹配滤波结合下延技术可以逐步细分位场信号。 1.3 方法流程 利用改进型正则化下延和匹配滤波相结合的方法进行深源位场信号提取的流程如图5所示,即首先对下延后位场数据进行浅源匹配滤波获得浅源位场,而后剥离浅源场从而求得深源场。 图5 方法流程图Fig. 5 Flow chart of the method 为测试上述思路处理效果,首先采用理论模型方式。组合模型由三层11个长方体组成(图6、表2,不考虑剩磁),地磁场50000 nT、偏角5°、倾角45°。数值计算采用长方体磁场无解析奇点表达式,组合模型距地面500m高度的垂直磁化磁异常如图6(c)。 图6 理论磁异常模型Fig. 6 Synthetic magnetic modela-模型平面投影;b-模型分布立体图(红色块体:0.2 SI;蓝色块体:0.04 SI);c-500m高空垂直磁化磁异常图a-projection of cuboids on the horizontal plane;b-perspective view of the test model (red blocks: 0.0126 SI; blue blocks: 0.0025 SI);c-magnetic anomaly fill contours at height of 500m 对上述500 m高度及其稳定下延500 m后磁异常计算径向平均对数功率谱,结果如图7所示。可以看出,两条曲线均可近似拟合为三条线段,只是下延者更为明显。 表1 长方体组合模型参数Table 1 Parameters of each prism in the synthetic model 图7 径向平均对数功率谱Fig. 7 Radially averaged log arithrn power spectrum1-下延500 m;2-z=-500 m1-downward continued 500 m; 2-z=-500 m 为与传统异常分离方法对比并计算误差,首先计算出A层模型在500 m高空和地面上的垂直磁化异常(图8(a)和(b))以及全部组合模型在地面的垂直磁化异常(图8(c)),根据这些计算结果,方法试验分为几个方面: 图8 深部弱信号提取模型实验结果Fig. 8 Deep weak signal extraction of synthesized modela-500 m高空深源场磁异常;b-地面深源场磁异常;c-全部组合模型在地面上的磁异常;d-全部组合模型在500m高空的ΔT下延至地面后,进行深部信号提取;e-匹配滤波提取结果;f-小波分解提取结果;g-向下延拓与匹配滤波相结合提取;(h)e-b、(i) f-b、(j)g-b:三种方法提取的深源场与理论深源场之间的差值Synthetic magnetic field anomaly of model A with I=90° at horizontal plane of (a) z=-500 m, (b) z=0m; (c) synthetic magnetic anomaly of all models with I=90° at z=0m; (d) downward continued (7(c)) to horizontal plane of z=0 m; spearated deep weak anomaly from (7(c)) using (e) matched filter; (f) the wavelete(db4) transform at order 4, and (g) impoved method; (h) difference between (b) and (e); (i) difference between (b) and (f); (j) difference between (g) and (b) (i) 将图7(c)下延至地面得到图8(d);与图8(c)对比,形态十分吻合,且保幅性较好; (ii) 对图7(c)作匹配滤波得到500 m高空的深源磁异常(图8(e)); (iii) 采用db4小波对图7(c)进行四阶小波分解得到500 m高空的深源磁异常(图8(f)); (iv) 采用稳定下延与匹配滤波相结合的方法,对图7(c)进行深源磁异常提取,即对图8(d)进行匹配滤波,得到地面上的深源磁异常(图8(g))。 将应用(ii), (iii), (iv)三种方法得到的深源磁异常分别与理论值对比,其误差分布如图8(h)、(i)、(j)所示。显然,第(iv)种方法得到的深源异常具有较高的保真度,而直接对原始异常进行匹配滤波或者小波多尺度分解提取的深部信号都比理论值大很多,分离不彻底。 从模型实验的结果可以看出,向下延拓可以有效的增强异常横向分辨率,一定程度上放大深部异常,改变异常体相对延拓面的深度,使深、浅场源在功率谱上更容易区分。不论是匹配滤波,还是小波多尺度分解,都能够不同程度地剥离浅部干扰异常,得到深部弱异常,虽然有所失真,但能够提取弱异常的基本特征。 选取大冶铁矿铁山南缘地区1∶1万航磁测区进行实例研究,研究区地质简图①如图9所示。 大冶铁(铜)矿床位于铁山岩体南缘中段与三叠系下统大冶组大理岩的接触带上。已有学者利用重磁观测资料对大冶铁矿区进行了反演和综合解释工作(杨宇闪等,2006;高宝龙等,2010),并取得了较好的地质效果。区域内地表基岩出露较好,岩性主要为闪长岩、含石英闪长斑岩、透辉石闪长岩、黑云母透辉石闪长岩等。不同岩性的侵入岩具有不同的磁性,磁化率变化范围为500×10-5~12000×10-5SI。黑云母透辉石闪长岩、闪长岩、粗斑含石英闪长斑岩、细斑含石英闪长斑岩、透辉石闪长岩斑状花岗闪长岩,磁化率依次减弱。 图9 铁山南缘地区地质简图Fig. 9 Simplified geological map of the southern margin of Tieshan1-含石英闪长斑岩;2-粗斑含石英闪长斑岩;3-闪长岩;4-透辉石闪长岩;5-闪长斑岩;6-黑云母透辉石闪长岩;7-斑状花岗闪 长岩;8-巨斑状闪长岩;9-第四系;10-水体;11-废石堆;12-断裂1-quartz-bearing diorite porphyry; 2-macroporphyaitic quartz-bearing diorite porphyry; 3-diorite; 4-diopside diorite; 5-porphyritic dio- rite; 6-biotite diopside diorite; 7-porphyritic granodiorite; 8-porphyritic diorite; 9-Quaternary; 10-water; 11-dump; 12-fault 图10 铁山南缘地区航磁图Fig. 10 Aeromagnetic anomalies in the southern margn of Tieshana-ΔT化极;b-下延150m;c-视深度1409 m深部磁异常;d-视深度1562 m深部磁异常a-reduction-to-the-pole (RTP) filed of ΔT;b-downward continuation of RTP field of 150 m;c-magnetic anomaly at apparent depth 1409 m;d-magnetic anomaly at apparent depth 1562 m 区内存在一长约5 km、宽约1 km的磁异常带(以500 nT等值线为界),可细分为铁门坎、龙洞-尖林山、象鼻山、狮子山-尖山四个较完整、独立的磁异常,并在南侧伴生负异常(图10(a))。 各类闪长岩均能引起一定强度的异常,其中黑云母透辉石闪长岩在本区出露最多、规模最大,因而产生了较高的背景场,规模远大于矿体,岩体产生的磁异常与矿体异常混叠在一起,为直接识别矿致异常尤其是深源弱异常增加了难度。 首先将航磁ΔT异常下延150 m,异常形态与原始异常形态基本一致,但正异常和负异常均有所增强,梯度带更加明显;原始异常中表现不明显的地方,下延后突出了其双峰的特点(如龙洞-尖林山一带)。而后利用匹配滤波方法,分离出视深度1409 m和1562 m的深部信号,如图(c)、(d)所示,可以看出,西北和东北段已没有明显的局部异常,推测上述地段1562 m以下没有更大磁铁矿存在,但狮子头尖山处还有1200 nT的闭合异常,而且正负伴生,负异常较周围更强,表明该地段深部仍有磁性地质体存在,说明此地磁性矿体有向下延伸的可能。 本文所述位场向下延拓方法,在延拓精度和稳定性上都有很大提升,改进的正则化方法在抑制噪声的同时不会压制低频成分,可使延拓结果更保幅;稳定向下延拓方法在提取深部弱信号中可以发挥一定作用,既可以使弱信号得到增强,同时也增大深源与浅源相对延拓面的埋深差异,在功率谱上更容易分辨。其后通过频谱分析和匹配滤波,剥离浅部异常及干扰,可获取目标深度的弱信息,为分析磁性体垂向延伸或确认盲矿提供依据。 匹配滤波建立在谱分析基础之上,只能分辨出不同频段的异常,而磁异常是叠加场,其高频成分除浅部异常或干扰外,尚含深部磁性体的异常边缘部分,造成磁异常频谱的频率混叠,因而不能完整无损的分离出深部信号。 [注释] ① 中国国土资源航空物探遥感中心.2006. 1∶10 000湖北黄石地区航空物探(磁)勘查成果报告[R]. Bian Guang-lang, Zhai Guo-jun, Gao Jin-yao, Zhu Dan, Li Lian-deng, Fang Jian-xun, Li Yan. 2014. Improved Talylor series approach for stable downward continuation of total strength of geomagetic field[J]. Acta Geodaetica et Cartographica Sinica, 43(1): 30-36(in Chinese) Cao Xin-zhi, Zhang Wang-sheng, Sun Hua-shan. 2009. Progress in the study of deep exploration in China[J]. Geological Science and Technology Information, 28(2): 104-109(in Chinese) Chen Long-wei, Hu Xiao-ping, Wu Mei-ping, Ma Tao. 2012. Research on spatial domain continuation method for potential field[J]. Progress in Geophysics, 27(4): 1509-1518(in Chinese) Dolmaz M N, Hisarli Z M, UstaoT, Orbay N. 2005. Curie point depths based on spectrum analysis of aeromagnetic data, West Anatolian extensional province, Turkey[J]. Pure and Applied Geophysics, 162: 571-590 Fuhry M., Reichel L. 2012. A new Tikhonov regularization method[J]. Numerical Algorithms, 59(443-445) Gao Bao-long, Tao De-yi,Zhan Ying-lin, Fan Zhi-xiong, Zhou-kui. 2010. Application of aero-surface and borehole magnetic exploration to the prospecting of exhausted mines in the Daye iron mine[J]. Geology and Exploration, 46(3): 483-490 (in Chinese) Guan Zhi-ning, Hao Tian-yao, Yao Chang-li. 2002. Prospect of gravity and magnetic exploration in the 21st century[J]. Progress in Geophysics, 17(2): 237-244 (in Chinese) Guo Cheng-bao, Xiao Chang-han, Liu Da-ming. 2008. Research on the continuations of magnetic field of magnetic object based on integral equation method and singular value decomposition[J]. Acta Physical Sinca, 57(7): 4182-4187(in Chinese) Li Y G, Devriese S. 2009. Enhancement of magnetic data by stable downward continuation for UXO applications[J]. Geoscience & Remote Sensing IEEE Transactions on, 51(6):3605-3614 Li Y G, Oldenburg D W. 2003. Fast inversion of large-scale magnetic data using wavelet transforms and a logarithmic barrier method[J]. Geophysical Journal International, 152(2):251-265 Liang Jin-wen. 1989. Downward continuation of regularization methods for potential fields[J]. Acta Geophysica Sinica, 32(5): 600608(in Chinese) Liu Qing-song, Wang Bao-ren. 1996. Vertical separation of potential field by using multiple matchedfilter[J]. Computing Techniques for Geophysical and Geochemical Explortion, 18(4):279-286(in Chinese) Liu Tian-you, Liu Da-wei, Zhan Ying-lin, Zhang Xiao-liang. 2006. The application of new magnetic data processing methods to the potentiality exploration in crisis mines[J]. Geophysical & Geochemical Exploration, 30(5):377381(in Chinese) Liu Yun-xiang. 2007. Processing and application of weak gravity and magnetic anomaly[J]. Progress in Exploration Geophysics, 30(6): 444-448 (in Chinese) Pawlowski R S. 1994. Green's equivalent-layer concept in gravity band-pass filter design[J]. Geophysics, 59(1):69-76 Spector A, Grant F S. 1970. Statistical models for interpreting aeromagnetic data[J]. Geophysics, 35(2):293-302 Syberg F. 1972.A Fourier method for the regional-residual problem of potential fields[J]. Geophysical Prospecting, 20(1):47-75 Xu P L. 1998. Truncated SVD methods for discrete linear ill-posed problems[J]. Geophysical Journal International, 135:505-514 Xu Y, Hao T Y, Li Z W,Duan Q L, Zhang L L. 2009. Regional gravity anomaly separation using wavelet transform and spectrum analysis[J]. Journal of Geophysics and Engineering, 6:279-287 Xu S Z, Shen X H, Zou L J, Yang H. 2004. Downward continuation of aeromagnetic anomaly from flying altitude to terrain[J]. Chinese J. Geophys., 47(6):1127-1130 (in Chinese) Yang Wen-cai. 1986. A generalized inversion technique for potential field data processing[J].Acta Geophysica Sinica, 29(3):283-291(in Chinese) Yang Yu-shan, Liu Tian-you, Li Yuan-yuan. 2006. 3D visualized inversion on the gravimagnetic field of arbitrarily shaped bodies using numerical integration method[J]. Geology and Exploration, 42(5): 79-83 (in Chinese) Zeng X N, LiX H, SuJ, Liu D Z, Zou H X. 2013. An adaptive iterative method for downward continuation of potential-field data from a horizontal plane[J]. Geophysics, 78(4): J43-J52 Zhang H L, Ravat D, Hu X Y. 2013. An improved and stable downward continuation of potential field data: The truncated Taylor series iterative downward continuation method[J]. Geophysics, 78(5): J75-J86 Zeng Xiao-niu, Li Xi-hai, Han Shao-qing, Liu Dai-zhi. 2011. A comparison of three iteration methods for downward continuation of potential fields[J]. Progress in Geophys., 26(3): 908-915(in Chinese) Zeng Xiao-niu, Liu Dai-zhi, Li Xi-hai, Niu Chao, Yang Xiao-jun, Lu Shi-kun. 2014. An improved iteration Wiener filter for downward continuation of potential fields[J]. Geophys., 57(6): 1958-1967(in Chinese) [附中文参考文献] 卞光浪,翟国君,高金耀,朱 丹,李连登,方建勋,李 研.2014.总强度磁场稳健向下延拓的改进泰勒级数法[J]. 测绘学报, 43(1):30-36 曹新志, 张旺生, 孙华山. 2009.我国深部找矿研究进展综述[J]. 地质科技情报,28(2):104-109 陈龙伟,胡小平,吴美平,马 涛.2012.空间域位场延拓新方法研究[J]. 地球物理学进展,27(4):1509-1518 管志宁,郝天珧.2002.21世纪重力与磁法勘探的展望[J]. 地球物理学进展,17(2):237-244 郭成豹,肖昌汉,刘大明.2008.基于积分方程法和奇异值分解的磁性目标磁场延拓技术研究[J]. 物理学报,57(7):4182-4187 高宝龙,陶德益,詹应林,范志雄,周 逵.2010.大冶铁矿接替资源勘查项目中“空、地、井”磁法测量的应用[J]. 地质与勘探,46(3):483-490 梁锦文.1989.位场向下延拓的正则化方法[J]. 地球物理学报,32(5):600-608 刘青松,王宝仁.1996.应用多次匹配滤波技术进行垂向位场分离[J]. 物探化探计算技术,18(4):279-286 刘天佑,刘大为,詹应林,张效良.2006.磁测资料处理新方法及在危机矿山挖潜中的应用[J]. 物探与化探,30(5):377-381 刘云祥.2007.重磁弱异常处理研究与应用[J]. 勘探地球物理进展,30(6):444-448 徐世浙,沈晓华,邹乐君,杨华.2004.将航磁异常从飞行高度向下延拓至地形线[J]. 地球物理学报,47(6):1127-1130 杨文采.1986.用于位场数据处理的广义反演技术[J]. 地球物理学报,29(3):283-291 杨宇山,刘天佑,李媛媛.2006.任意形状地质体数值积分法重磁场三维可视化反演[J]. 地质与勘探,42(5):79-83 曾小牛,李夕海,韩绍卿,刘代志.2011.位场向下延拓三种迭代方法之比较[J]. 地球物理学进展,26(3):908-915 曾小牛,刘代志,李夕海,牛 超.2014.位场向下延拓的改进迭代维纳滤波法[J]. 地球物理学报,57(6):1958-1967 Extracting Weak Magnetic Signals at Depth from Aeromagnetic Anomaly Data GUO Zhi-kui2, ZHANG Qing-shan1, 2, CHEN Chao2, DAI Ji-shu1,CHEN Hai-di1,SUN Kai2, WANG Qiu-ge2 (1.GeophysicalExplorationAcademyofChinaMetallurgicalGeologyBureau,Baoding,Hebei071000;2.HubeiSubsurfaceMulti-scaleImagingKeyLaboratory,InstituteofGeophysicsandGeomatics,ChinaUniversityofGeosciences,Wuhan,Hubei430074) Magnetic anomalies are superposition of magnetic field anomalies of geological bodies at different depths in the subsurface. In aeromagnetic surveys, such signals from depth are generally weak and gentle, with low resolutions in both horizontal and vertical directions. Thus they are difficult to extract from aeromagnetic data processed and interpreted. To solve this problem, this work uses the high-precision and stable downward continuation method to enhance amplitudes of magnetic anomalies. With decreasing distances between the continuation plane and field source, the apparent depth difference between shallow and deep magnetic signals increases progressively. So they can be distinguished on the logarithm power spectrum. Then the shallow signals are removed by the matched filter to isolate the deep signals. Meanwhile the apparent depths of these deep signals can be calculated. deep weak signal, downward continuation, matched-filter, spectrum analysis 2015-02-09; 2015-08-08;[责任编辑]郝情情。 国家“973”计划课题(编号 2012CB416805)和科研院所基本科研资金资助项目(编号 WHS201211)联合资助。 郭志馗(1990年—),男,在读博士,主要从事重磁位场数据处理、反演方法研究。E-mail:zhikuiguo@live.cn。 张青杉(1968年—),男,中国冶金总局物勘院副总工程师,主要从事地球物理勘探与研究工作。E-mail:qingshan-zhang@163.com。 P631 A 0495-5331(2015)06-1007-9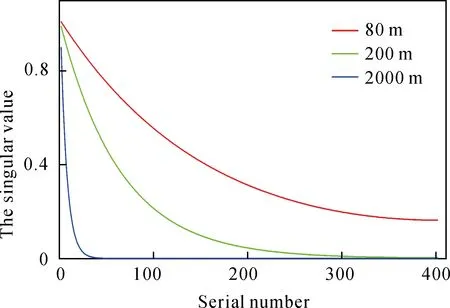



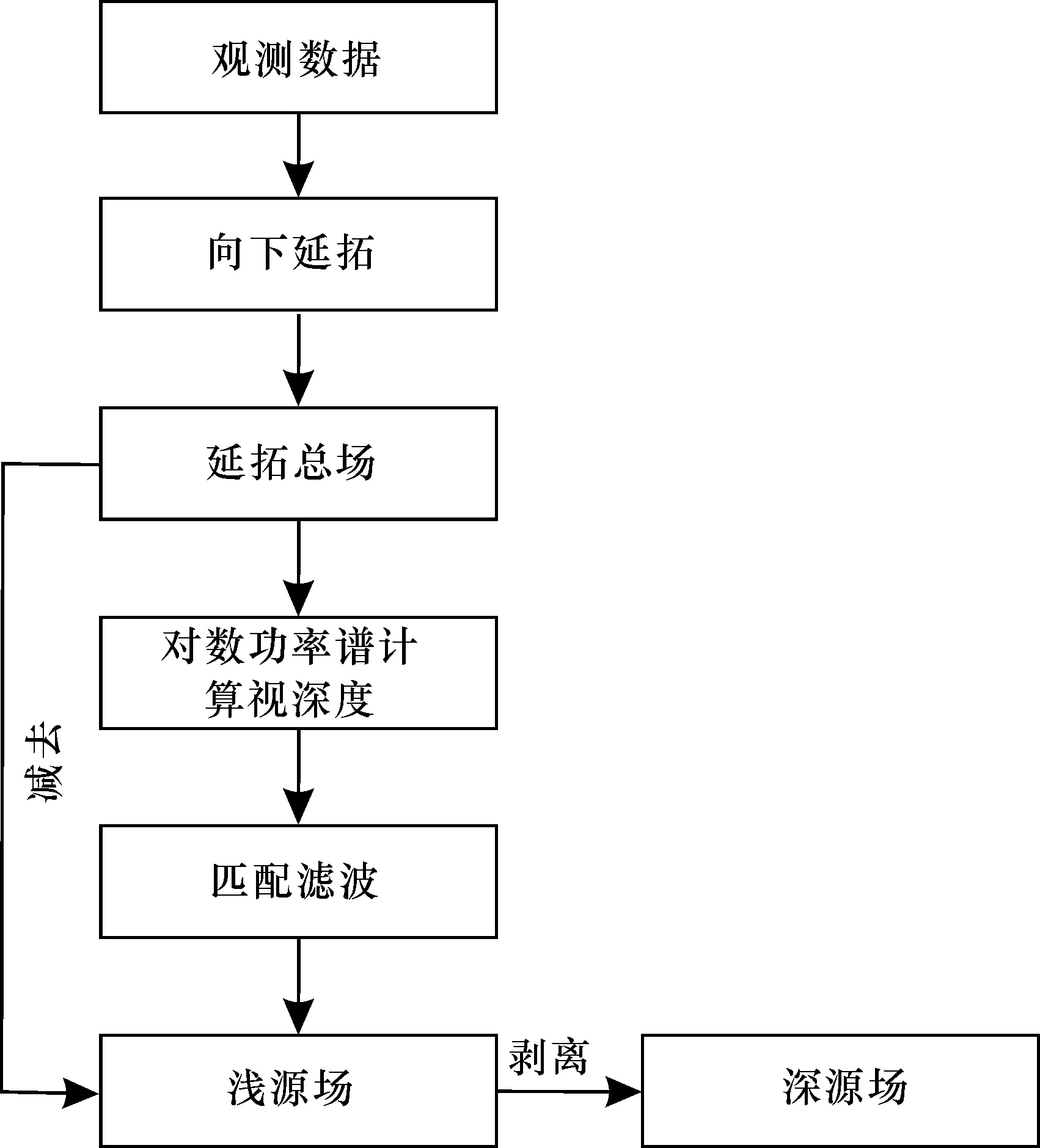
2 模型实验

3 实例分析


4 结论

