共沸点存在的充分条件*基金资助:清华学堂人才培养计划
梁妍钰
(清华大学化学系 北京 100084)
共沸点存在的充分条件*基金资助:清华学堂人才培养计划
梁妍钰
(清华大学化学系 北京 100084)
以纯液体蒸气压和亨利系数为出发点,讨论了二组分气液相图存在共沸点的充分条件。结合纯液体蒸气压和亨利系数的物理意义,对共沸点存在的条件进行了说明。
二组分气液相图 共沸点 亨利常数 纯液体饱和蒸气压 定标粒子理论
1 问题的提出
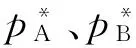
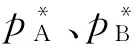
这样,也就能够得到理想溶液二组分体系的p-x图(图1)。

图1 二组分理想溶液的p-x相图
在讨论完理想液体的情况后,自然而然地,要引入真实液体的二组分气液相图。真实液体的二组分相图可以分为两类:① 有共沸点;② 无共沸点。共沸点在p-x图上非常容易辨认,因为除了图线两端气、液相线相交之外,共沸点是气、液相线在图上的唯一交点。其唯一性可以利用吉布斯相律说明(以S表示化学物种数;P表示相数;R表示化学平衡数;R′表示其他制约条件数;f表示体系自由度):
S=2,P=2,R=0
由于在共沸点要求气、液相组成相同,所以:
R′=1
f=S-R-R′-P+1=1-2+1=0
关于共沸点的存在条件,有下述说明[1]:与理想溶液差别不大时没有共沸点;与理想溶液差别较大时存在共沸点。这个说明比较模糊,也没有指出具有差别的物理量是什么。本文将在下面简要讨论这种“差别”具体指什么,即给出二组分气液体系中存在共沸点的条件。
2 问题讨论
在讨论真实溶液的情况时,需要将决定蒸气压的公式中的x换成活度a,在这里,取参考态Ⅰ的活度,推导过程如下:
aA=aA(xA,p)
考虑外压不变的情况(外压可以通过惰性气体调节),而体系中的p仍定义为pA+pB,而不包括惰性气体贡献的部分。于是:
aA=aA(xA)
而在气相中,有:
pA=pyA
通过pA作为桥梁:
化简得:
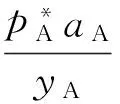
在共沸点处有:
yA=xA
yB=xB
则
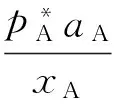
可化为:
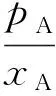
式中pA、pB表示当前A、B在气相中的压力。
从图2可以较容易地看出这种关系。
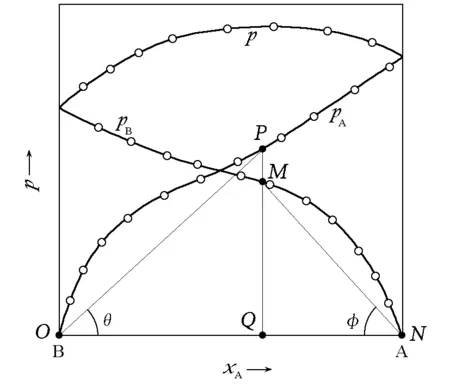
图2 pA和pB随组成的变化
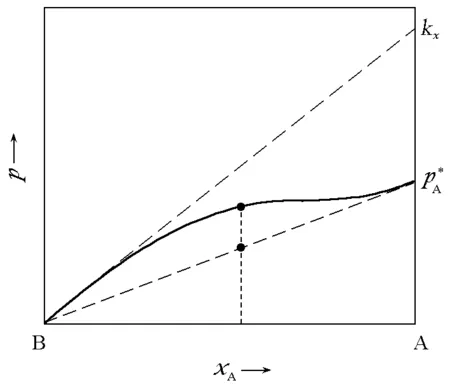
图3 pA与kx,A和的关系

图时,不动点一定存在的示意黑球要滚动到另一个黑点处,白球也同理。由于滚动是个连续的过程,所以球在滚动过程中不能离开轴,故必然存在某个时刻黑白两球在轴上某点相遇。该点即为正切值相等(tanφ=tanθ)的点。
这里需要说明,由于二组分均为正(负)偏差的体系远多于偏差方向不同的体系,所以图5列出的一些情况也许并不存在对应的真实体系。
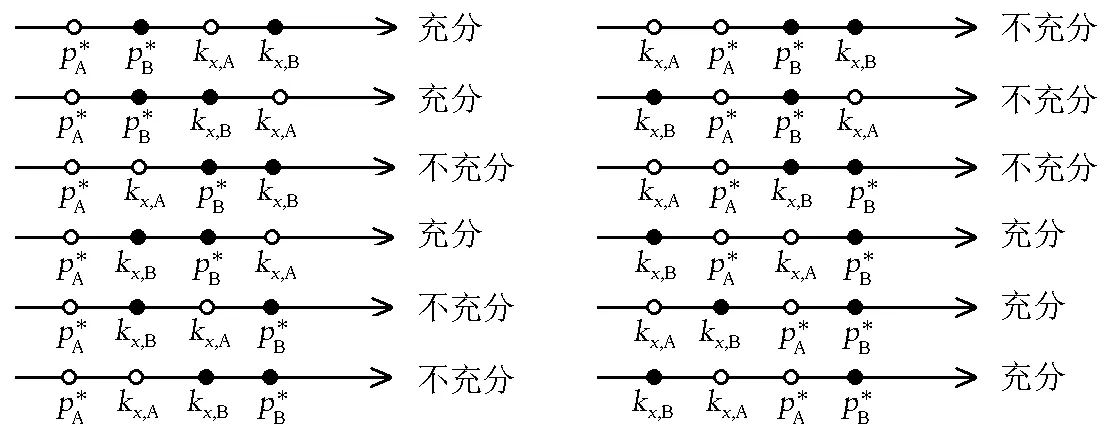
图时相对位置的所有可能的情况此图是图4的一个扩展,展示了的情况下所有可能的相对位置,图中“充分”表示在该相对位置下一定存在共沸点;“不充分”表示在该相对位置下不一定存在共沸点。
另一个需要说明的是共沸点的性质。从所给出的例子可以发现,共沸点总是相图的极值点。这一点可以被证明是正确的。
极值条件:
(1)
吉布斯-杜亥姆公式:
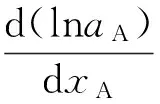
(2)
将式(2)代入式(1),得:
(3)
根据共沸条件:
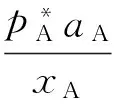
(4)
故式(4)可化为:
(5)
可以发现:式(5)是式(3)=0成立的充分条件。通过上述讨论可以发现,满足共沸条件的点一定是压力对组成的一阶导数等于0的点。这样,共沸点可以被更准确地称为最低(高)共沸点(拐点的情况很少见)。
3 问题的结论
本文讨论了二组分气液相图共沸点存在的充分条件,并进一步指出共沸点一定可在极值处得到。至此,可以对文章开头提到的“差别”做出一个较为准确的论述。
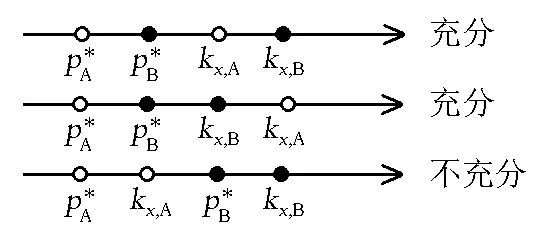
为简单起见,仅考虑两组分均为正(负)偏差的情况。这时可以笼统地说:亨利系数间和纯液体蒸气压(下称为拉乌尔系数以与亨利系数相对应)间的距离小于上述二者之间的差距时,共沸点一定存在;相反,如果每个组分的拉乌尔系数和亨利系数之间的距离小于其与另一组分的拉乌尔系数的差距,那么共沸点一定不存在。
以上完全是由数学推导得出的结论,比较抽象,将之回归到物理图像上会清晰许多。根据定标粒子理论[2],亨利常数可以表示为如下形式:
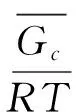
(6)
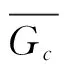
图且A、B均为正偏差时的所有情况
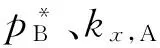
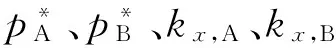
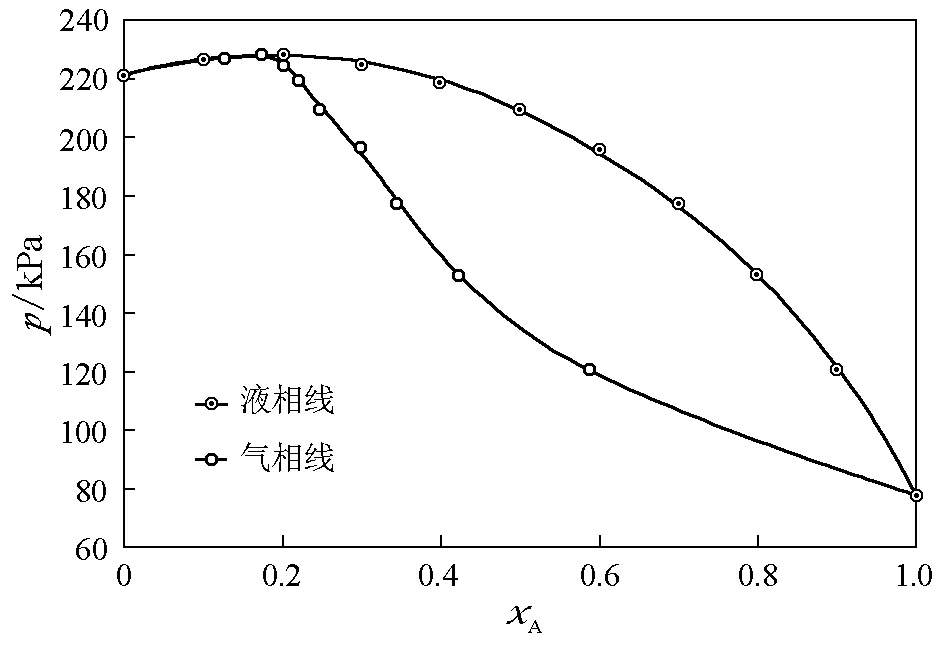
图7 1-丁醇(A)-环己烷(B)体系(383.15K)=77.7kPa,=222.0kPa,kx,A=283.4kPa,kx,B=511.0kPa
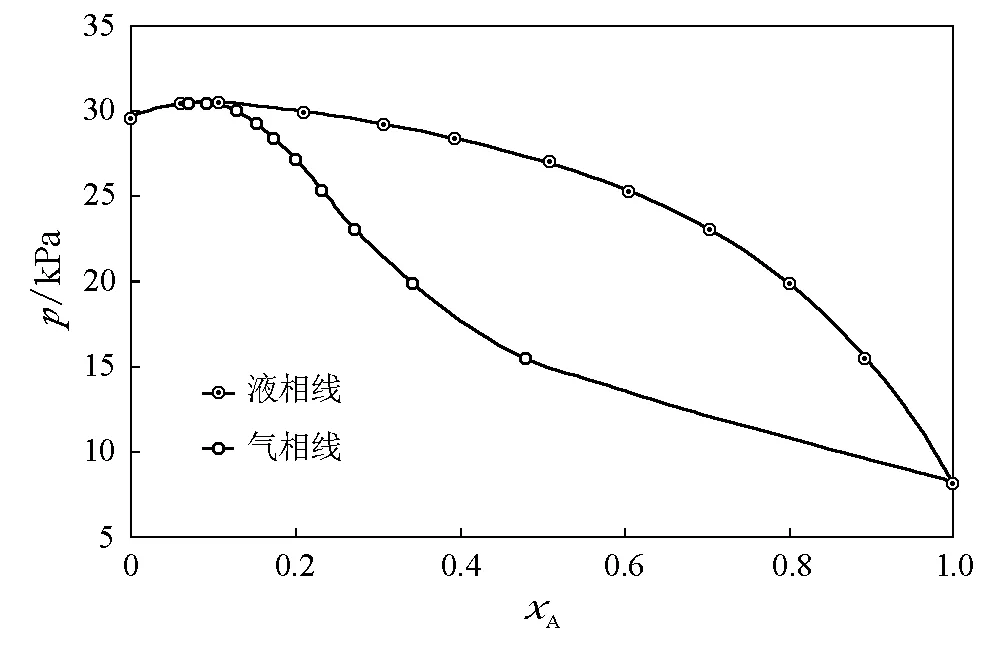
图8 2-丁醇(A)-苯(B)体系(318.15K)=8.1kPa,=29.7kPa,kx,A=42.9kPa,kx,B=77.6kPa

图9 2-丙醇(A)-苯(B)体系(298.15K)=5.9kPa,=12.5kPa,kx,A=37.4kPa,kx,B=44.4kPa
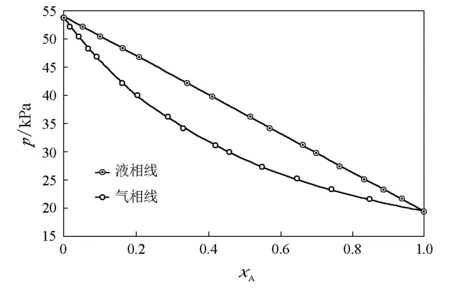
图10 甲苯(A)-苯(B)体系(334.15K)=19.3kPa,=54.0kPa,kx,A=23.3kPa,kx,B=55.8kPa
4 问题的延伸
本文认为体系的亨利系数与拉乌尔系数的相对大小关系是共沸点存在与否的一个判据。这个结论与柯诺瓦洛夫-吉布斯定律有密切联系。为方便起见,做如下定义(tanθ含义如图2所示):
于是有:

(7)
式中πA、πB分别为A、B在p-x图对应的tanθ和tanφ(图2)。由于式(7)分母为πA和πB的加权平均,所以分母的值一定在πA和πB之间,故而当且仅当πA大于πB时,yA>xA。而柯诺瓦洛夫-吉布斯第一定律[3]叙述说蒸气中总是富集能使总蒸气压升高的物种,其中“富集”的含义是气相浓度高于其液相浓度。于是可以推论:如果存在共沸点,则在相图的两个端点附近富集的一定是不同物种。而式(7)的结论告诉我们:蒸气富集的物种一定具有更大的π值。所以在相图的两个端点处,πA和πB的相对大小一定是不同的;而且在端点附近有:
所以共沸点存在的充分条件可以表述为:
上式包含了图5中标为“充分”的所有情况;图5中的其余情况也可能存在共沸点,但该共沸点将是拐点而非极值点。从总体上看,本文所得结论和柯诺瓦洛夫-吉布斯定律的叙述是一致的,但对于相图是否能够存在拐点,还需要有更进一步的讨论。
[1] 傅献彩,沈文霞,姚天扬.物理化学.北京:高等教育出版社,1990
[2] Pierotti R A.ChemRev,1976,76(6):717
[3] 韩德刚,高执棣.化学热力学.北京:高等教育出版社,1996

中国化学会2015年部分学术会议计划
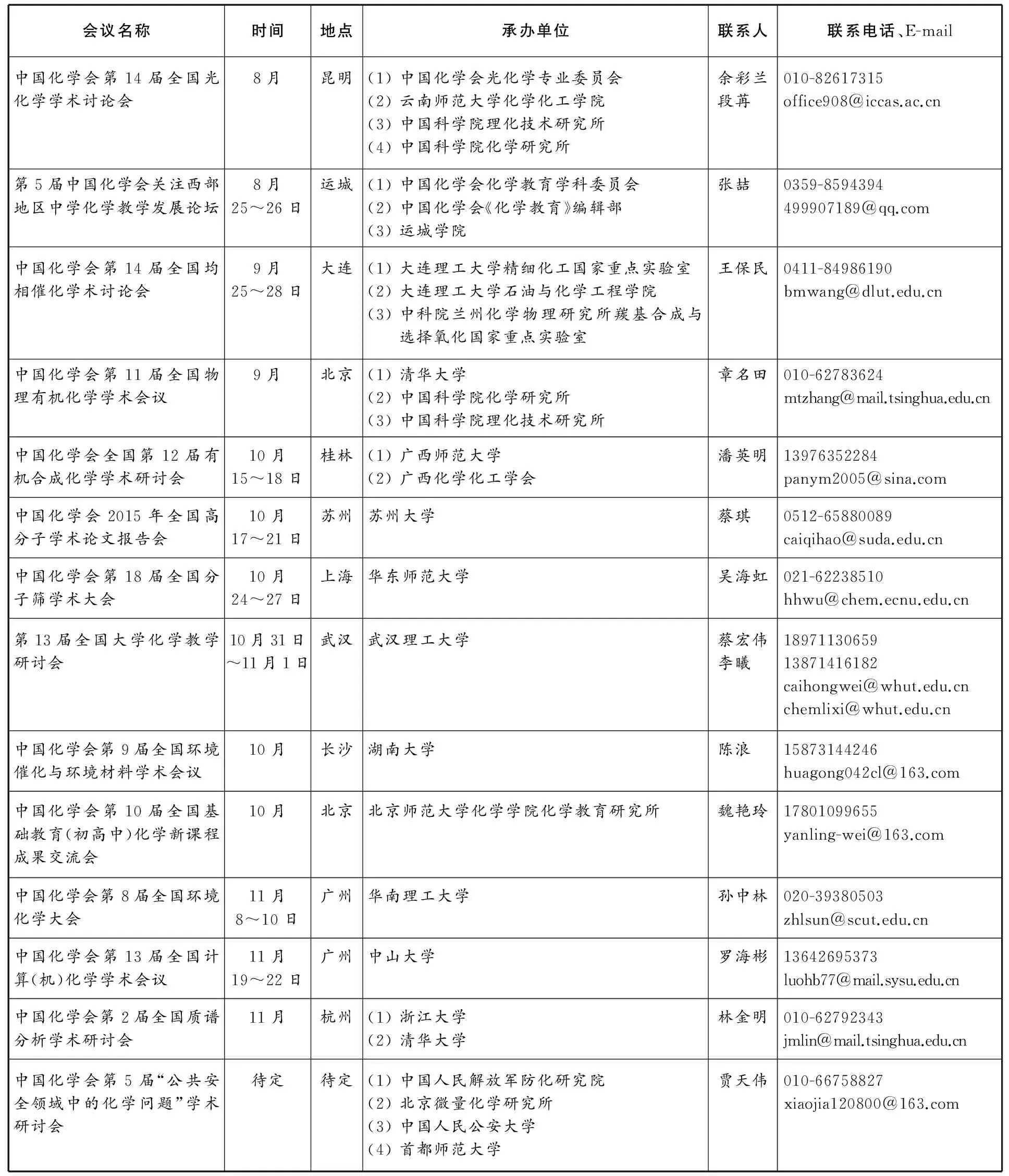
续表
详细内容请参见中国化学会网页:http:∥www.chemsoc.org.cn
Sufficient Conditions for Existence of the Azeotropic Point*
Liang Yanyu
(DepartmentofChemistry,TsinghuaUniversity,Beijing100084,China)
Starting from the saturated vapor pressure of pure liquid and the Henry constant, this article discusses the sufficient conditions of the existence of the azeotrope point in two-component liquid-vapor phase diagrams. Furthermore, the conclusion is illustrated by examples, combined with the physical meaning of these constants.
Two-component liquid-vapor phase diagram; Azeotrope point; Henry constant; Saturated vapor pressure of pure liquid; Scaled particle theory
O642;G64

