基于料斗秤的定量装车系统算法

董秀明，李丽宏，韩芝星

(太原理工大学信息工程学院，山西太原030024)

0 引言

料斗秤［1］以其拥有较高的计量效率、适用于非粘性散状物料的称量等优点和特点，在交通运输、工业生产等部门尤其在以煤炭为原材料的企业中得到广泛应用。经研究分析，在定量装车系统中存在两方面的问题:1)在料仓卸料过程中，由于物料的下落冲击和卸料阀门开启/闭合的冲击，造成称重传感器输出信号中含有较多的噪声信号;2)在长期使用过程中，称重传感器还会产生不同程度的老化，甚至损坏造成严重的称量误差或导致系统故障。针对上述问题，首先，替代传统的滑动平均滤波处理方法［2］，利用小波变换［3］算法对称量信号中的噪声信号进行降噪处理;其次，针对传感器老化、故障的问题，利用径向基(RBF)神经网络［4］算法逼近多路称重传感器之间的关系，预测各传感器的输出，进行故障传感器的判断，并在某一只称重传感器失效情况下给出估算值替代其信号，得到校正称量数据，并给出传感器故障信号。

1 料斗式定量装车系统

定量装车系统主要由欧姆龙PLC、高性能工业控制仪表、液压动力控制单元、上位机控制软件、料斗秤等组成。

本文对料斗秤的动态称重过程进行研究，提出了应用Donoho软阈值小波算法［5］进行降噪处理，同时采用径向基神经网络算法对故障称重传感器信号进行处理。

如图1所示，定量装车系统中，在对车辆车型、装载量等信息收集后，将车辆放行至固定装载区，车辆位置调整准确后，开始装车。装车方式可以选择手动或是自动。

如图2所示，物料从筒仓落料口进入料斗秤，落料速度由落料口处的平板阀控制，当落料量达到设定值时关闭平板阀。称重料斗由4只安装于支撑框架上的称重传感器支撑。物料下落到料斗后，其重量经料斗传递到称重传感器，传感器产生与重量呈正比例的电信号输入二次仪表，仪表将物料重量上传给上位机与设定装载量进行实时比对，控制进行多次装载，当达到设定装载量后停止装车，车辆驶离装载区。

2 动态称重数据滤波处理

图1 定量装车系统流程图Fig 1 Flow chart of quantitative loading system

图2 料斗秤结构示意图Fig 2 Structure diagram of Hopper scale

料斗秤上传感器采集到的称重信号存在一定的噪声信号，为了得到光滑、平稳的信号，需要对采集到的信号进行降噪处理。由于小波变换对非平稳的噪声信号具有很好的滤波效果，而在处理料斗秤称重传感器信号的过程中不能产生附加震荡，故本文采用小波变换中的Donoho软阈值法对4路称重传感器信号进行滤波，得到平稳的称重信号。

小波软阈值函数为

其中，wi为小波系数，wi为降噪后的小波系数，a为阈值。

原始信号长度为N，噪声方差为σ2，此处选择全局统一阈值，选取公式为

本文以山西某煤矿定量装车料斗秤某一路称重传感器采样数据为例，通过小波分解后，对处理后的信号进行重构。为验证算法有效性，采用Matlab中的wavedec()和waverec()函数对实际称重信号进行分解和重构。此处选用db3小波基，对信号做5层分解，先对细节系数成分进行抑制，通过抑制后的系数重建小波。原始信号如图3所示。

对携带噪声信号的原始信号小波5级分解后的第1～5层细节系数，如图4所示。

经过5层分解后，测量序号被划分为0～32，33～233，234～280三个区间，对应于向料斗秤中装料前、装料中和装料完成三个过程。对称量信号降噪后，得到降噪后有效信号，如图5所示。

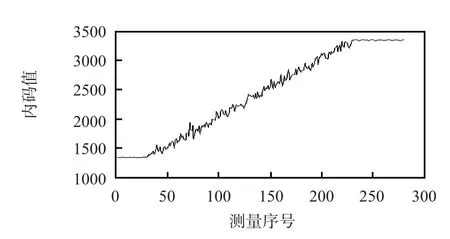
图3 含噪声信号的原始信号Fig 3 Original signal containing noise signal

图4 用db3小波进行5层分解后的第1～5层细节系数Fig 4 The 1～5 layer detail coefficient produced by db3 wavelet 5 level decomposition

图5 降噪后有效信号Fig 5 Effective signals after noise reduction

3 故障称重传感器诊断

利用径向基神经网络对料斗秤称重传感器故障进行诊断，是利用径向基神经网络逼近4路传感器之间的函数关系，从而预测出各传感器的输出。通过将预测值和实际值作为输入，建立监测模型。

3.1 传感器故障诊断原理

如图6所示，基于料斗秤的定量装车系统分别独立采集4路称重传感器的重量内码向量X(x1，x2，x3，x4)。经过预估网络求得预估信号向量 Xr(x1r，x2r，x3r，x4r)，将向量 X和Xr进行比较判断，进而判断传感器是否故障，如果传感器无故障，直接用向量X计算料斗秤称重结果;反之，设第2只传感器故障，则由预估数据x2r替代原来重量内码x2，融合成新的重量内码向量 Xf(x1，x2r，x3，x4)，再计算出称重结果，其他传感器故障算法同理。

3.2 径向基神经网络模型的建立

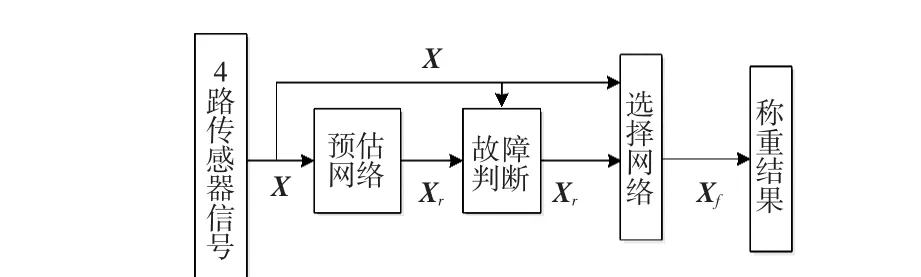
图6 智能容错判断Fig 6 Intelligent fault tolerant judgment

料斗秤的4路称重传感器的输出之间存在某种函数关系，第i(取1，2，...，4)路称重传感器的输出是其他3路的函数，即

利用径向基神经网络逼近式(3)的四传感器关联函数，完成任一传感器的输出估计，广义神经网络模型如图7所示。

图7 径向基神经网络预测输出模型Fig 7 Predicted output model for radial basis neural network

预估输出向量为 Xr(x1r，x2r，x3r，x4r)，其计算公式为

其中，b为输出层偏置值，w为径向基神经网络的权值向量，且 w=［w1，w2，w3，…，wm］T，w0=1，u 为径向基函数向量。

人工神经网络中，权值表示神经元节点中间的关联强度，神经网络将知识存储在调整后的权值中。所以，实际应用中，计算预估输出向量的关键是权值的求取。

本文中隐含层基函数选取为高斯函数

其中，|xk-xj|为欧几里德距离

σ为标准差，其计算公式为

式中 dmax为所选取的中心最大距离，n为隐含节点的个数。

用伪逆法求得输出权值w，在这里期望输出为原始数据中d={xij}。xij为第i个输入向量在第j处的期望输出值。wij，i=1，2，3…I;j=1，2…J 为第 i个隐藏节点导第 j个输出节点的权值，则输出权值可用下式求出［6］

其中，G+={gkj}，矩阵 w=wij

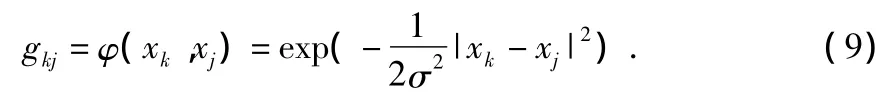
径向基函数中心确定方法有4种［7］，随机选取固定中心，自组织选取中心，有监督选取中心，正交最小二乘法。此处选择随机选取固定中心的方式进行网络训练，这种方法的好处是避免径向基函数出现过尖或过平的情况。

3.3 称重传感器的融合故障判断

该方法只考虑在同一时刻，料斗秤上的4路传感器中只有1路传感器数据异常。设xn，k为标准重量的物料加载在料斗里的不同位置时称重传感器n的输出信号，^xn，k是通过上述模型得到的该传感器的预测值，设εn为该传感器的监测阈值，当该传感器发生故障时，满足

其中，xn_r为称重传感器的量程。连续采样m次，如果每次都满足上式，则判断该传感器故障。

本文采用多组历史检测数据进行神经网络训练。每次训练时，径向基神经网络的输入向量为3个，输出向量为4个。该神经网络共有4个输入节点，隐含层有20个节点。设定均方误差(MSE)目标值为0，学习率为0.005，设定所有的遗忘因子均为0.85。经多次训练，在隐含层神经元个数为10时，预测模型的效果最好。

以该煤矿定量装车料斗秤称重传感器内码为例，由于煤料下落位置偏向3#，4#传感器一侧，故1#，2#传感器内码偏小如表1所示。

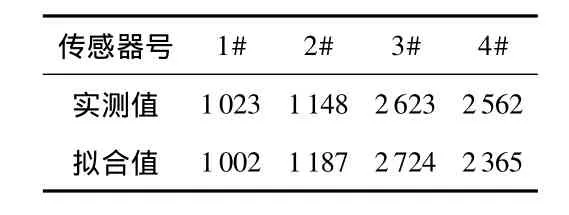
表1 各路称重传感器内码Tab 1 Each path weighing sensor ISN

4 结束语

本文针对基于料斗秤的定量装车系统中的动态称量信号分析，采用小波变换中的Donoho软阈值法对称量信号进行降噪处理;之后利用径向基神经网络建立预测模型，进行故障传感器的判别并给出估算值替代测量值。通过实践证明:该方法具有较强的实用性，减小了噪声对称重数据的影响，提高了系统的称量精度，去除了传感器故障对系统可靠性的影响。

［1］郑 娟.料斗秤控制系统［J］.信息技术，2006，29(10):145-147.

［2］胡 松，江小炜，杨 光，等.滑动平均滤波在微弱脉冲信号检测中的应用［J］.计算机与数字工程，2007，35(10):169-171.

［3］龙 洋，游勇华，于伟臣，等.基于Matlab小波去噪方法及应用研究［J］.数字技术与应用，2012(8):51-52.

［4］籍晋鹏，李 丽.基于智能容错算法的多传感器皮带秤［J］.传感器与微系统，2014，33(11):41-43，47.

［5］方 勇，戚飞虎.基于软阈值的小波图像增强方法［J］.计算机工程与应用，2002，38(23):16-19.

［6］杨 静，李丽宏.基于专家系统的汽车衡故障传感器判别［J］.传感器与微系统，2014，33(11):34-36.

［7］周开利，康耀红.神经网络模型及其 Matlab仿真程序设计［M］.北京:清华大学出版社，2005.