基于横摆力矩控制的电动轮自卸车制动力分配策略
李 勇,凌 云,罗树英
(湖南工业大学 电气与信息工程学院,湖南 株洲 412007)
基于横摆力矩控制的电动轮自卸车制动力分配策略
李 勇,凌 云,罗树英
(湖南工业大学 电气与信息工程学院,湖南 株洲 412007)
电动轮自卸车在左右附着系数不同的路面进行紧急制动时,会产生干扰横摆力矩,导致自卸车侧滑跑偏。为此,提出了一种基于横摆力矩控制的电动轮自卸车制动力分配策略,该策略采用参数模糊自整定PID控制器,根据横摆角速度偏差值分别调整制动时自卸车左轮和右轮的滑移率,自动分配左轮和右轮的制动力来直接实现横摆力矩控制。仿真分析结果表明:系统能够很好地实现电动轮自卸车制动力的合理分配;采用制动力分配策略后,最大侧滑距离从8.9 m减小为0.72 m。
电动轮自卸车;制动力分配;横摆力矩;模糊自整定
0 引言
电动轮自卸车行驶过程中常会面临恶劣路况,且其在左右附着系数相差较大的情况下进行紧急制动时,两侧轮胎的制动力也相差较大。直线行驶的电动轮自卸车在干扰横摆力矩作用下会跑偏,甚至出现侧滑现象。因此,有较多科研工作者对干扰横摆力矩的控制进行了研究[1-3]。如文献[1]采用了线性增益的横摆力矩生成方式对车辆横摆力矩增益进行调度控制,这种基于比例的反馈控制方法简单易用,调整方便。但是,当车辆的系统参数、路面附着情况发生变化时,这种方法缺乏足够的适应能力。文献[2]基于模糊逻辑方法提出了一种车辆稳定控制系统,该系统增强了车辆在转弯和直线行驶时的稳定性,但是它的控制精度和动态品质还较差。文献[3]采用了二自由度控制结构,提出了一种将前馈补偿器与反馈控制器相结合的控制方法。前馈补偿器将车辆的质心侧偏角控制在一个比较小的范围内,通过前馈加快系统的响应。而反馈控制器采用了线性二次型最优调节(linear quadratic,LQ)方法设计反馈系数,用来消除受控变量的稳态误差。从本质上来讲,LQ方法属于线性控制方法,对于车辆这种包含有轮胎等大量非线性特性部件的系统来讲,缺乏一定的鲁棒性。
在电动轮自卸车中,可以通过驱动电机较为方便地实现对车轮转矩的控制。因此,本文提出一种采用直接横摆力矩控制的方法,以实现对车辆制动稳定性的控制,并通过系统仿真验证了所提方法的有效性。
1 电动轮自卸车动力学模型
电动轮自卸车的动力学模型如图1所示。
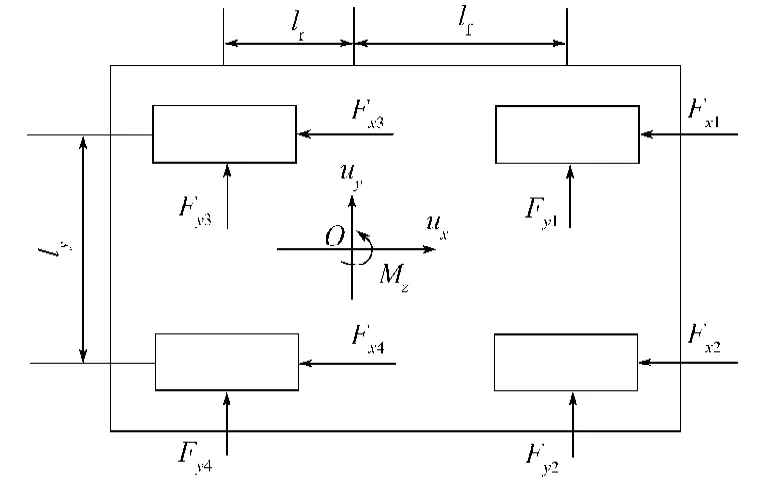
图1 电动轮自卸车动力学模型Fig.1 Dynamic model of electric wheel dump truck
该模型中,不考虑空气阻力、侧倾和车轮滚动阻力等的影响,只考虑自卸车沿x轴、y轴的平移和绕轴横摆3个自由度的运动,并假定对前轮不施加转向操作,可建立如下车辆运动基本方程[4-5]:
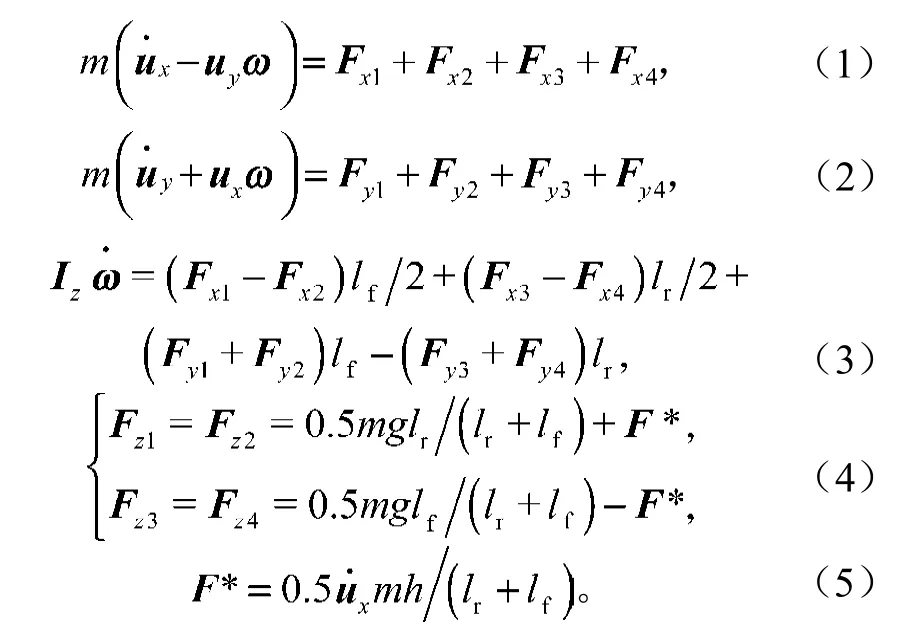
以上各式中:m为整车质量;
ux,uy为自卸车沿x轴、y轴的速度;
lf,lr为质心距前、后轴距离;
h为自卸车质心高度。
自卸车行驶轨迹偏离预期行驶轨迹的距离为Sy,设自卸车在t=0时刻开始制动,初始偏移Sy(0)=0,则其在t时刻的偏移为

轮胎模型采用H. B. Pacejka等人提出的轮胎力数学模型[6-7],当不考虑轮胎外倾角及漂移的影响时,有

式(7)中:x为输入,它可以是轮胎滑移率s或侧偏角 ,当输入为轮胎滑移率s时,输出为轮胎纵向力Fxi;当输入为轮胎侧偏角 时,输出为轮胎侧偏力Fyi;
B, C, D, E均为轮胎模型参数,其中B为刚度因子,C为形状因子,D为峰值因子,E为曲率因子。
前后轮胎的侧偏角分别为[5]

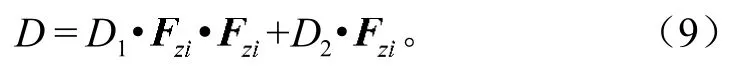
式(9)中,D1, D2为峰值因子的载荷回归参数。
2 制动力分配策略
电动轮自卸车的系统控制目标为:减少自卸车制动后的横摆角速度偏差,并使其趋近于0;控制方法为:以左右车轮滑移率作为输出量,当左右车轮附着系数相差较大时,根据检测到的干扰横摆角速度改变左右车轮的制动力至接近相等,达到自卸车制动稳定的目的。电动轮自卸车的控制系统结构如图2所示。
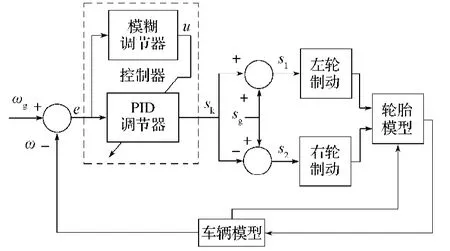
图2 控制系统结构图Fig.2 Control system structure
控制器根据横摆角速度偏差值e进行控制,输出车轮滑移率调整值sk,分别调整制动时左轮和右轮的滑移率,自动分配左轮和右轮的制动力。以右轮附着系数低为例,当右轮制动力减小时,自卸车产生逆时针方向横摆力矩,横摆角速度偏差值e小于0,控制器输出的滑移率调整值sk小于0,右轮滑移率增加,但是因附着系数低,制动力变化不大;左轮滑移率减小,左轮产生的制动力减小,导致逆时针方向横摆角速度减小。
3 控制器设计
电动轮自卸车的控制器采用参数模糊自整定PID控制器。在自卸车的制动过程控制中,首要考虑的是系统稳定性要求[8],因此,控制器中的模糊调节器只对PID调节器的比例系数Kp进行自整定。Kp增大可加快系统响应速度,提高系统调节精度,但过大将会导致系统不稳定。Kp参数的自整定规则如下:
1)e偏大时,取较大的Kp值,加快调节作用;
2)e中等时,取中等的Kp值,保持调节作用;
3)e偏小时,取很小的Kp值,尽量减小调节作用,以避免控制器在横摆角速度目标值附近进行频繁调节。
在模糊控制系统中,E为横摆角速度误差e绝对值的量化值,模糊子集为{ZO,PS,PM,PB};U为模糊控制器输出u的量化值,模糊子集为{ZO,PM,PB}。高斯型隶属函数如图3所示。

图3 隶属度函数Fig.3 Membership functions
控制系统的模糊控制规则见表1,规则的制订原则是减小在横摆角速度目标值附近的调节力度,保证自卸车制动的平稳性。

表1 模糊控制规则Table 1 Fuzzy control rules
4 系统仿真
仿真试验车辆为154 T电动轮自卸车。根据已有的轮胎特性[6-7],满载时,在不同附着系数工况路面下,仿真电动轮自卸车的纵向附着系数与滑移率的关系曲线如图4a所示,电动轮自卸车的侧向附着系数与侧偏角的关系曲线如图4b所示,拟合式(7)中的回归参数见表2。

图4 自卸车轮胎附着系数曲线Fig.4 Dump truck tire adhesion coefficient curve
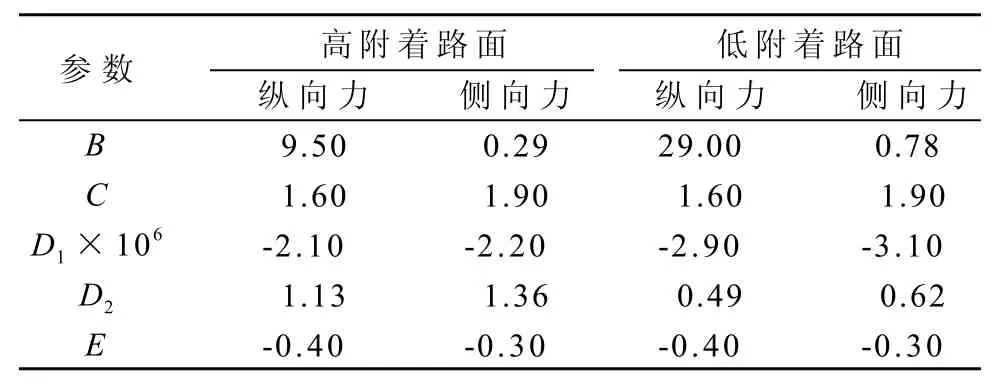
表2 轮胎模型参数Table 2 Tyre model parameters
按照图2所示的控制系统,利用Matlab进行仿真试验。仿真模型采用Simulink搭建,将其中的轮胎模型编写成Matlab函数嵌入到Simulink仿真模型中[9]。左轮制动与右轮制动主要考虑电动轮制动环节的惯性与延迟,为了简化计算,在轮胎模型中考虑制动力比例系数,将电机作为二阶系统来进行研究,则电机的输入转矩与作用到车轮上的输出转矩可以用下式来表示[10]:
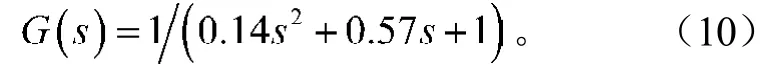
PID调节器的控制参数为

在进行制动仿真试验时,模拟自卸车在36 km/h的初速度下进行制动。制动开始时,自卸车左侧轮胎处于高附着系数的路面上,右侧轮胎处于低附着系数的路面上;低附着系数的路面长10 m,宽4 m;当自卸车前进10 m,或者是向左偏移2 m后,右前轮进入高附着系数的路面,稍后,右后轮也进入高附着系数的路面。
自卸车制动时,车轮滑移率给定值sg为0.18,当不采取制动力分配策略以及人工转向等辅助措施时,其仿真制动过程如图5所示。

图5 无制动力分配策略时自卸车制动过程Fig.5 Dump truck brake process without braking force distribution strategy
由图5可知,当无制动力分配策略以及人工转向等辅助措施时,自卸车系统的制动时间为3.7 s;由图5所示纵向制动过程中制动距离随时间变化的曲线,可以得出自卸车系统的最大制动距离为23.0 m;而由图5中的侧滑过程中侧滑距离随时间变化的曲线,可以得出自卸车系统的最大侧滑距离最终达8.6 m,这一数值显然超出了大多数路面的宽度。
采用图2所示的系统进行制动力分配,制动时车轮滑移率给定值sg仍为0.18,所得自卸车仿真制动过程如图6所示。
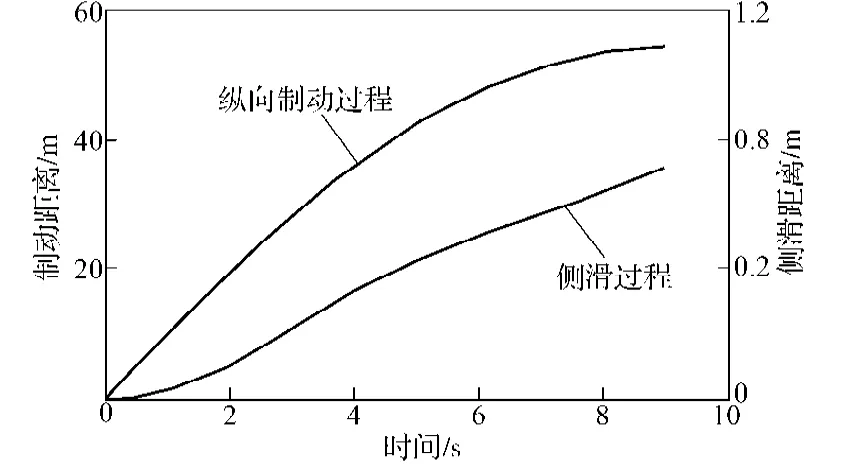
图6 采用制动力分配策略时自卸车制动过程Fig.6 Dump truck brake process with braking force distribution strategy
由图6可以看出,采用制动力分配策略时,自卸车系统的制动时间增大,达9.0 s;由图中所示自卸车纵向制动过程中制动距离随时间变化的曲线,可知自卸车系统的最大制动距离增大至54.0 m,出现这一结果的原因,可能是控制系统自动控制高附着系数侧的制动力与低附着系数路面的制动力匹配,自卸车总制动力下降;由图中所示自卸车侧滑过程中侧滑距离随时间变化的曲线可知,系统的最大侧滑距离大大减小,仅为0.72 m。
从自卸车的仿真侧滑过程曲线可以看出,制动开始4 s后,自卸车侧滑偏移从非线性变化转换为线性变化,非线性变化对应的是左右附着系数不同的路面。当驶出附着系数不同的路面后,在横摆力矩的作用下,自卸车已经形成了一定的偏转角。因此,在后面的制动过程中,尽管左右路面的附着系数已经相同,但是自卸车仍然会随着制动距离的增加,侧偏距离增加。可见,所提出的制动力分配控制策略和控制方法是可行的。
5 结论
基于横摆力矩的电动轮自卸车制动力分配控制策略,能控制车辆的侧滑偏移,使其最大侧滑距离大大减小,从而保持车辆制动时具有良好的稳定性和安全性。在直接检测车辆侧滑偏移量困难的情况下,车辆横摆角速度测量相对简单,所提出的制动力分配控制策略和控制方法可行。
参数模糊自整定PID控制器在横摆角速度与目标值偏移较大时,调节力度加大;横摆角速度接近目标值时,调节力度很小,符合人工控制的习惯。控制器在自动保持车辆制动稳定性的同时,增大了制动距离,制动效果降低,因此,是否进行相应的制动力分配控制,可视实际控制过程具体情况而定。
[1] Makoto Kamachi, Kevin Walters. A Research of Direct Yaw-Moment Control on Slipperyroad for in-Wheel Motor Vehicle [C]//The 22st International Battery, Hybrid and Fuel Cell Electric Vehicle Symposium & Exposition. Yokohama:[s.n.],2006:2122-2133.
[2] Farzad Tahami, Shahrokh Farhangi, Reza Kazemi. A Fuzzy Logic Direct Yaw-Moment Control System for All-Wheel-Drive Electric Vehicles[J]. Vehicle System Dynamics, 2004, 41(3):203-221.
[3] Motoki Shino, Naoya Miyamoto, Wang Yuqing, et al. Traction Control of Electric Vehicles Considering Vehicle Stability[C]//The 6th International Workshop on Advanced Motion Control. Agoya:IEEE Press,2000:311-316.
[4] Boada B L, Boada M J L, Diaz V. Yaw Moment Control for Vehicle Stability in a Crosswind[J]. International Journal of Vehicle Design, 2005, 39(4):331-348.
[5] 赵 伟,魏 朗,杜 峰. 基于横摆力矩的汽车制动稳定性模糊控制[J]. 长安大学学报:自然科学版,2008,28 (6):76-80.Zhao Wei, Wei Lang, Du Feng. Fuzzy Control of Automobile Braking Stability Based on Yaw Moment Control[J]. Journal of Chang’an University:Natural Science Edition,2008, 28(6):76-80.
[6] Pacejka H B, Besselink I J M. Magic Formula Tyre Model with Transient Properties[J]. Vehicle System Dynamics,1997,27:234-249.
[7] 边明远.用于纵向道路附着系数评估的简化轮胎模型[J].重庆理工大学学报:自然科学版,2012,26(1):1-5.Bian Mingyuan. Simplified Tire Model for Longitudinal Road Friction Estimation[J]. Journal of Chongqing University of Technology:Natural Science, 2012, 26(1):1-5.
[8] 唐国元,宾鸿赞. 基于模糊模型的车辆稳定性控制方法研究[J]. 中国机械工程,2004,15(22):2064-2067.Tang Guoyuan, Bin Hongzan. A Study on Stability Control of Vehicle Based on Fuzzy Model[J]. China Mechanical Engineering,2004,15(22):2064-2067.
[9] 杜 峰,闫光辉,陈 涛. 基于Matlab系统函数法的汽车轮胎力计算研究[J]. 机械科学与技术,2013,32(6):909-913.Du Feng, Yan Guanghui, Chen Tao. Calculation of Vehicle Tire Force Based on Matlab System Function[J]. Mechanical Science and Technology for Aerospace Engineering,2013,32(6):909-913.
[10]尚明利.混合动力汽车再生制动与稳定性集成控制算法研究[D].长春:吉林大学,2011.Shang Mingli. Researched on Regenerative Braking and Stability Integration Control Algorithm for Hybrid Electric Vehicle[D]. Changchun:Jilin University, 2011.
[11]钟坤炎,易灵芝.基于模糊自适应PID控制的SRD研究[J].湖南工业大学学报,2008,22(5):28-31.Zhong Kunyan,Yi Lingzhi.Research on SRD Based on Fuzzy Adaptive PID Control[J]. Journal of Hunan University of Technology,2008,22(5):28-31.
[12]易江义,周彩霞,刘楚达. 改进型BP神经网络PID控制在自动化测试装置中的应用研究[J]. 湖南工业大学学报,2007,21(1):84-88. Yi Jiangyi, Zhou Caixia, Liu Chuda. Application Study on Improved BP Neural Network PID Controller in Servomechanism[J]. Journal of Hunan University of Technology,2007,21(1):84-88.
[13]彭国谱,贺 翔,唐华平,等. 矿用自卸车车架的有限元分析及优化设计[J]. 湖南工业大学学报,2014,28(3):35-40. Peng Guopu, He Xiang, Tang Huaping, et al. Finite Element Analysis on Mining Dump Truck Frame and Its Optimization Design[J]. Journal of Hunan University of Technology,2014,28(3):35-40.
(责任编辑:廖友媛)
EBD Strategy of Motorized Wheel Dump Truck Based on Yaw Moment Control
Li Yong,Ling Yun,Luo Shuying
(School of Electrical and Information Engineering,Hunan University of Technology,Zhuzhou Hunan 412007,China)
During the emergency braking on the road with different left and right adhesion coefficients, the motorized wheel dump truck will emerge interferential yaw moment, leading to the dump truck side slip and deflection. Therefore, puts forward a kind of EBD(electronic brake force distribution) strategy of motorized wheel dump truck based on yaw moment control. The strategy adopts the parameter fuzzy self-tuning PID controller which can adjust the slip ratios of the left and right wheels of the dump truck respectively during the emergency braking according to the yaw velocity deviation value and realize the direct yaw moment control by the automatic brake force distribution of the left and right wheels. Simulation analysis shows that the system realizes the reasonable brake force distribution of the motorized wheel dump truck, and the maximum side slip distance decreases from 8.9 m to 0.72 m.
motorized wheel dump truck;EBD (electronic brake force distribution);yaw moment;fuzzy self-tuning
U463.5;TH248
A
1673-9833(2015)02-0084-05
10.3969/j.issn.1673-9833.2015.02.016
2015-01-20
湖南省自然科学基金资助项目(13JJ9016)
李 勇(1989-),男,湖南浏阳人,湖南工业大学硕士生,主要研究方向为电气自动化控制,E-mail:790531717@qq.com

