各向异性分层介质电磁场并矢Green函数的混合算法

陈桂波，潘轶群，张烨

（1.长春理工大学 理学院，长春 130022；2.长春市农业机械研究院，长春 130062）

积分方程法是求解层状介质三维电磁正演问题的一种常见方法，该方法的难点在于如何计算层状介质的并矢Green函数（Dyadic Green’s Function，DGF），许多学者对此类问题作了深入研究，但多数只局限于各向同性介质模型［1-3］，而针对各向异性介质的研究则相对较少［4，5］。对于相对比较简单的各向异性介质，如横向同性各向异性介质，其层状结构中的DGF一般也是由Sommerfeld积分组成，该积分的被积函数一般呈现出较强的振荡特性与慢衰减特性，从而导致数值计算非常缓慢，这往往成为实际应用中的瓶颈问题。因此，国内外许多学者对Sommerfeld积分的快速求解问题作了研究［6-9］，并开发出相应的快速算法，归结起来主要有：解析方法，改进的直接积分方法，滤波方法和复镜像方法。尽管存在以上多种快速算法，但各种方法都有其独特的适用条件，而且计算精度和计算效率对于介质参数、场源距离等因素的影响有很大程度的依赖关系，也就是说，没有哪一种方法能够满足所有条件下Sommerfeld积分的快速计算。因此，开发一种能够综合运用各种方法的优势并且根据参数条件自动选择最优计算方案以达到最佳计算效果的混合算法，具有十分重要的理论与实际意义。

1 各向异性分层介质电磁场DGF

考虑图1所示的N层各向异性介质（为简单起见，本文只考虑单轴各向异性介质），各个地层的层界面位置为dn(n=2,3,…,N)、复介电常数和 磁 导 率 为 对 角 张 量diag(μnh,μnh,μnv) (n=1,2,…,N)。其中分别表示第n层横向和纵向复介电常数，而μnh,μnv分别表示第n层横向和纵向磁导率。复介电常数ε*n由公式 ε*np=εnp+(iωε0ρnp)-1(p=h,v)确定，其中 εnp为相对介电常数，ρnh,ρnv分别表示第n层横向和纵向电阻率。

图1 各向异性分层介质地电模型

对于空间中任意的激发源分布(J,M)，假定时谐因子为 eiωt，i=-1，其产生的电场和磁场满足Maxwell方程组：

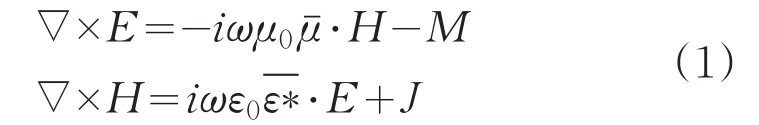
如果引入层状介质中的DGF，E,H解可表示为［5］：

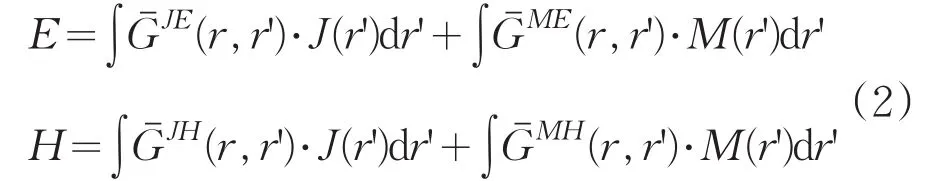
1.1 均匀各向异性介质DGF闭合解析计算

按Micalski（1997）所给的积分表达式，我们经过数学推导，得到了均匀各向异性介质中四种电磁场DGF的闭合解析解：

（1）电流源电场DGF解析解

其中α,β=x,y且α≠β，

（2）磁流源电场DGF解析解

其中

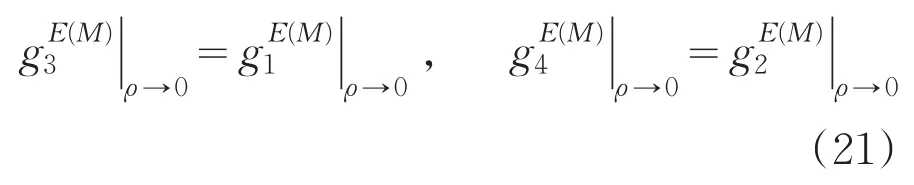
以上给出了电场DGF闭合解析解，相应的磁场DGF可由对偶原理得到［10］，限于篇幅，这里不给出其具体表达式。

1.2 DGF的Sommerfeld积分形式

根据Micalski（1997）的结果，层状各向异性介质中的DGF由下列几种形式的Sommerfeld积分组成：其中为传输线Green函数，文献［5］中给出了8种传输线Green函数的详细表达式，这里不再赘述。特别地，当ρ→0时，由Bessel函数的渐近性，式（22）-（24）的Sommerfeld积分有的变为0，有的变为普通的半无穷积分

2 各向异性分层介质DGF的混合算法

2.1 单一方法计算Sommerfeld积分的不足

（1）解析方法

解析方法一般利用数学推导给出Sommerfeld积分的解析表达式，由于其计算速度较快并且易于对物理现象的直观解释和理解，解析方法在均匀半空间以及一些特殊模型问题的计算与分析中占有重要地位。Sommerfeld、Foster和Wait等人在这方面做过深入的研究［6，12，13］，尤其是Sommerfeld经过复杂数学推导得到的Sommerfeld恒等式，至今仍在许多领域被广泛使用。解析方法的不足是应用范围十分狭窄，仅限于均匀介质、半空间以及一些较特殊的模型。

（2）基于直接积分的方法

直接积分法利用计算机程序，通过不断的外延积分进行Sommerfeld积分的高精度计算，其受参数影响较小，计算精度较高，但由于Sommerfeld积分被积函数的性质，该积分在积分路径上收敛缓慢。虽然一些学者对直接积分法作了改进，引入非线性变换手段来加速积分收敛［14，15］，但往往仍难以满足需要调用大量Sommerfeld积分的三维电磁模拟的计算。

（3）滤波方法

数字滤波技术诞生于上实际70年代初，由Ghosh首先使用［16］，之后Johnsen，Koefoed，Anderson等人对该方法作了改进和发展［17-19］。该方法通过输入函数（核函数）与滤波因子在给定长度下褶积求和从而快速得到积分近似值。由于避免了Bessel函数的计算和数值积分，使Sommerfeld积分的计算速度得到大大提高。但问题在于该方法对参数范围较为敏感，尤其是在横向距离ρ较小或较大的情况，由于核函数与Bessel函数相比变化剧烈，此时数字滤波方法的精度较差。

（4）镜像方法

镜像方法源于几何光学理论，在地电领域最早由Wait在计算半空间磁偶极子的辐射时引入［20］。而后，Lindell曾利用连续复镜像法计算Green函数［21］。近年来，离散复镜像法［22，23］在电磁学领域的应用越来越广泛，该方法利用现有的Bessel积分恒等式结合复指数序列逼近得到Sommerfeld积分的闭合解。其优点是计算速度很快，但适用条件较高，往往要求工作频率限定在某一范围内且源点和场点位于同一介质层中。

由前面的分析和讨论可知，Sommerfeld积分的各种计算方法都有其特殊的适用条件，而没有哪一种方法是一劳永逸的。因此，本文拟从参数条件出发，开发一种能够综合运用各种方法的优势并根据参数范围选择最优计算方案的高效混合算法。这里需要说明的是，本文所研究的算法主要是针对其在积分方程中的应用，而在利用积分方程法求解三维电磁问题时，一般计算量较大的是源点和场点位于同一地层或相邻地层时的DGF。由电磁理论，这时可将DGF分为对应均匀无限大介质中的直射项和反映地层边界条件的反射项。为了提高计算精度与效率，直射项采用前面推导出的DGF的解析式计算；而对于反射项，其所包含的Sommerfeld积分往往没有解析解，一般需要用数值方法来计算。

横向距离ρ趋近于零时DGF的计算是在三维电磁正演模拟中经常遇到的一个问题，但在以往相关文献中却很少被提及。本文在前面式（21）和式（25）已经给出了当ρ→0时直射项的解析解和反射项中Sommerfeld积分的表达式及计算方案，在精度允许范围内，一般ρ＜10-5即可以使用ρ→0时的结果来近似。当10-5≤ρ≤10-3或ρ≥103时，由于数字滤波方法对ρ很小或很大时特别敏感，若采用数字滤波方法可能会得到较大误差甚至错误结果，而基于直接积分的方法则受参数影响较小并且可以得到较高的精度，这里我们采用一种新近开发的使用高阶窗函数改良Sommerfeld积分被积函数的性质并结合非线性变换手段加速积分收敛的高效直接积分算法［20］。经过研究多种加快级数收敛速度的变换方法我们发现，使用连分式展开具有更好的收敛速度，图2为相同条件下分别使用连分式展开和欧拉变换［14］计算了均匀介质中磁流源磁场DGF的三个主分量，在精度相当的情况下两种方法所用计算时间分别为2.81、4.15秒，因此我们以高阶窗函数结合连分式展开法（HWCFM）作为改进的直接积分方法。当10-3＜ρ＜103时，由于我们需要计算的四种场型DGF的Sommerfeld积分的被积函数均不存在性质特别差的情况，因此采用数字滤波方法计算Sommerfeld积分一般可以得到较高的计算精度与效率。由于离散复镜像法的适用条件过于苛刻，因此我们在混合算法中暂不引入离散复镜像法。

图2 使用连分式展开与欧拉变换方法计算GMH三个主分量对比

归结上面的分析讨论，我们得到一种计算各向异性分层介质DGF的单点混合算法（SPHM）：并矢Green函数

2.2 DGF的混合算法

在利用DGF研究电磁辐射与散射问题时，往往需要计算沿某一方向或不同方向上的一系列场点的函数值，此时若采用直接的单点算法，虽然其中应用了一些加快计算速度的手段，但往往还是难以满足实际工作需要。对于一些特殊而用又常用的模型，我们充分考虑构成DGF的Sommerfeld积分被积函数的某些性质，得到一些计算速度更快且不失精度的全空间DGF的算法。

首先考虑对于固定的(z,z')，需要计算某一范围内的横向距离ρ对应的DGF值。当ρ≤10-3或ρ≥103时，采用前面介绍的SPHM计算。而对于实际中经常遇到的位于(10-3,103)范围内的多个ρ对应的Sommerfeld积分的计算，我们引入Anderson（1982）提出的延迟褶积算法，选择一个参数序列ρN+1-j=e-Δ(j-1)ρmax，j=1,2,…,N ，ρ1=ρmin，其中Δ为对数坐标下的滤波系数采样间隔，ρmax,ρmin分别为ρ的最大值和最小值。当 j=1时，计算全部滤波系数下的离散褶积，并保存所有的输入函数值。之后对于参数序列的每一次延迟即j=2,3,…,N，根据所选特殊参数序列的性质，输入函数的指标j分别相对于前一次时增加一个采样间隔，这时使用已保存的输入函数值和滤波系数做褶积求得 j=2,3,…,N时的Sommerfeld积分，最后利用插值方法可以快速得到[ρmin,ρmax]范围内所有的ρ对应的DGF，以上延迟褶积算法的详细过程参见文献［8］。本文将上述计算任意参数范围内多点DGF的算法简称为MPHM。MPHM大大提高了全空间上DGF的计算效率，图3（a）为使用MPHM与SPHM计算了三层介质电流源DGF分量，两种方法计算图中50个节点所用时间分别为0.61和0.96秒，可见引入MPHM使计算速度得到了较大提高。这里需要说明的是，本文SPHM和MPHM中使用的数字滤波方法都是变长度的自适应数字滤波方法［18］。

3 DGF混合算法应用

图3 应用MPHM与SPHM法计算三层介质中的DGF

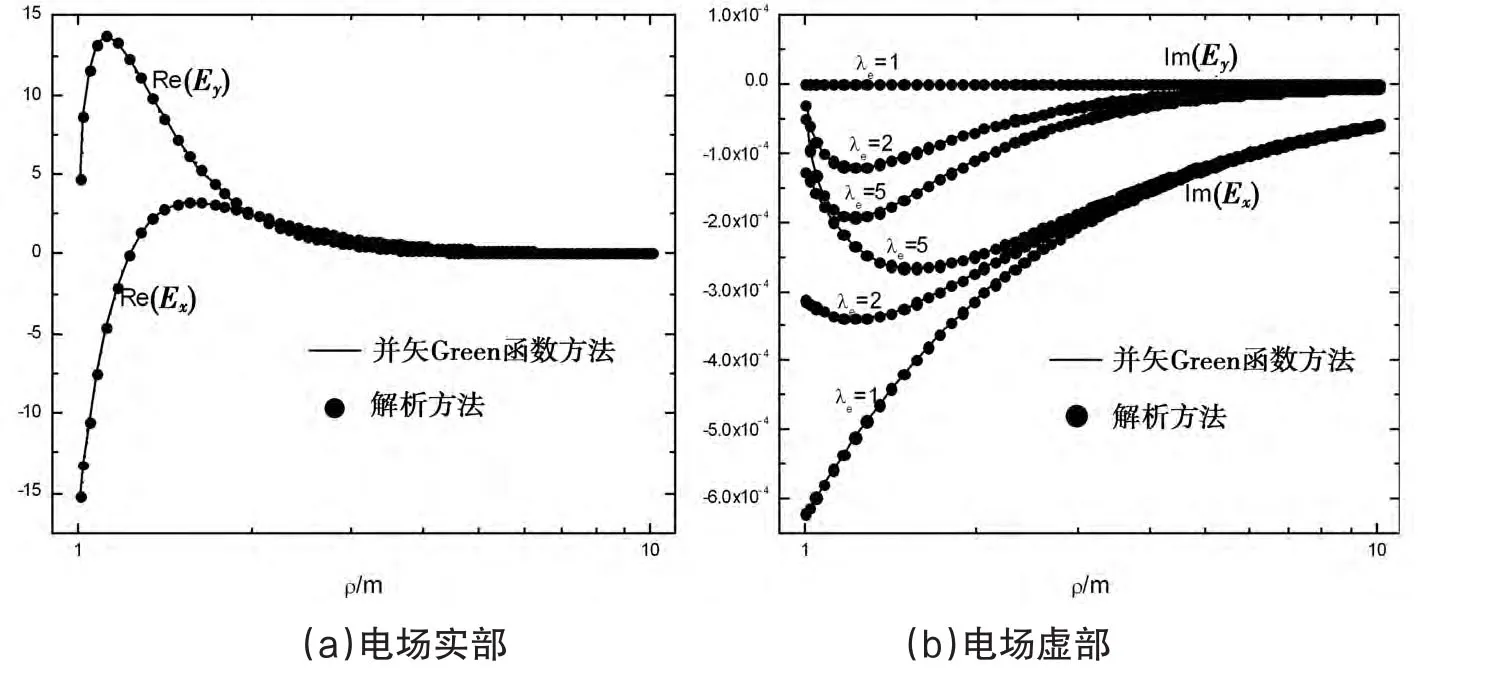
图4 本文方法与解析方法计算半空间介质表面电偶极子的辐射电场（地层的平均电阻率为100Ω⋅m，f=1000Hz）

考察源偶极子位于地表以及地中时的电磁辐射问题，本文所选用模型实例均假定为非磁性的。按照Wait的方法［13］，得到位于各向异性介质表面的水平电偶极子在地表产生的电场水平分量的解析式。令沿x轴方向的单位大小的电偶极子位于地表(x',y')处，则在地表(x,y)处产生的电场水平分量为其中和λe为半空间均匀介质的横向复介电常数和电各向异性系数，波数kh,ke的计算公式前面已经给出。图4为分别利用本文DGF方法和解析方法计算不同各向异性系数条件下均匀半空间介质表面的电偶极子辐射场，可以看出，两种方法计算的曲线基本一致，并且介质的各向异性对电场水平分量的实部几乎没有影响，但对虚部的影响却较明显。图5是利用本文算法计算半空间介质中的电偶极子辐射场，与文献［21］的结果吻合得较好。

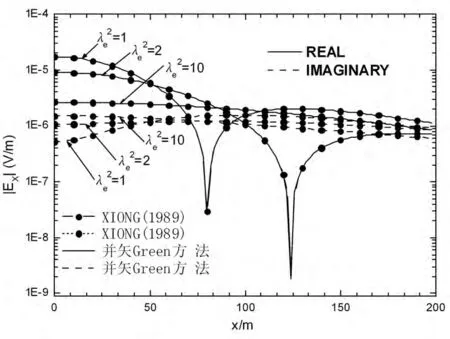
图5 本文方法与Xiong（1989）计算半空间介质中的偶极子辐射

本文中所有数值计算均是在同一台主频3.0GHz计算机上完成的。

4 结论

利用传输线Green函数和复变积分理论得到均匀介质中四种场型DGF的闭合解析解，并特别给出了场源横向距离趋于零时的解。对于层状介质中的Sommerfeld积分，对比分析各种算法的优缺点与适用条件，得到一种快速、高精度且不受参数范围限制的DGF的混合算法，并引入延迟褶积方法进一步加快特殊几何模型下全空间DGF的计算。研究DGF在计算层状各向异性介质偶极子辐射场以及积分方程中的应用，并得到了一些具有重要参考价值的数值结果。本文方法可直接用于积分方程法求解三维电磁正演问题，另外也可作为研究电导率与磁导率各向异性对地下资源勘探的综合影响的一种手段。

［1］Michiels B，Fostier J，Bogaert I，et al.Full-wave simulations of electromagnetic scattering problems with billions of unknowns［J］.IEEE Transactions on Antennas and Propagation，Publication，2015，63（2）：796-799.

［2］Wiedenmann O，Eibert T F.A domain decomposition method for boundary integral equations using a transmission condition based on the near-zone couplings［J］.IEEE Transactions on Antennas and Propagation，2014，62（8）：4105-4114.

［3］Markkanen J，Yla Oijala P.Discretization of electric current volume integral equation with piecewise linear basis functions［J］.IEEE Transactions on Antennas and Propagation，2014，62（9）：4877-4880.

［4］Xiong Zonghou.Induced-polarization and electromagnetic modeling of a three-dimensional body buried in a two-layer anisotropic earth［J］.Geophysics，1986，51（12）：2235-2246.

［5］MicalskiK A，Mosig JR.Multilayered media Green’s functions in integral equation formulations［J］.IEEE transactions on antennas and propagation，1997，45（3）：508-519.

［6］Sommerfeld A. Partialdifferentialequations in physics［A］.New York：Academic，1949.

［7］Cui T J.Fast evaluation of Sommerfeld integrals for EM wave scattering and radiation by three-dimensional buried objects［J］.IEEE Transactions on Geoscience and Remote Sensing，1999，37（3）：887-900.

［8］Anderson W L.Fast Hankel Transforms using related and lagged convolutions［J］.ACM Transactions on Mathematical Software，1982，8（4）：344-368.

［9］Aksun M I.A robust approach for the derivation of closed form green functions［J］.IEEE Trans.Microwave Theory Tech，1996，44（5）：651-658.

［10］Tai C T.Dyadic Green’s Functions in Electromagnetic Theory［A］.2nd ed.IEEE Press，New York，1993.

［11］Piessens R，Ede Doncker-Kapenga.QUADPACK：A SubroutinePackageforAutomaticIntegration［A］.New York：Springer-Verlag，1983.

［12］Campbell G A，Foster R M.Fourier Integrals for Practical Applications［A］.New York，Bell Telephone System，1931.

［13］WaitJR.Geo-electromagneticsm［M］.Academic Press，1982.

［14］Cornille P.Computation of Hankel transforms［J］.SIAM Rev，1972，14：278-285.

［15］Micalski K A.Extrapolation methods for Sommerfeld Integral Tails［J］.IEEE transactions on antennas and propagation，1998，46（10）：1405-1418.

［16］Johansen H K，Sorensen K.Fast Hankel transforms［J］.Geophysical Prospecting，1979，27（4）：876-901.

［17］KoefoedO，GhoahD P.Computationoftype curves for electromagnetic depth sounding with a horizontal transmitting coil by means of a digital linear filter［J］.Geophysical Prospecting.1972，20（2）：406-420.

［18］Anderson W L.Numerical integration of related Hankel transforms of orders 0 and 1 by adaptive digital filtering［J］.Geophysics，1979，44（7）：1287-1305.

［19］Wait J R.Image theory of a quasistatic magnetic dipole over a dissipative half-space［J］.Electron.Lett，1969，5（13）：281-282.

［20］陈桂波.各向异性分层介质中电磁场并矢Green函数的一种高效算法［J］.物理学报，2009，58（3）：1608-1618.

［21］Zonghou Xiong.Electromagnetic fields of electric dipoles embedded in a stratified anisotropic earth［J］.Geophysics，1989，54（12）：1643-1646.