一种混合深度网络的抗噪性能研究
王璟尧,刘云海
(1.浙江大学信息与通信工程研究所,杭州310027;2.浙江省综合信息网技术重点实验室,杭州310027)
一种混合深度网络的抗噪性能研究
王璟尧1,2,刘云海1,2
(1.浙江大学信息与通信工程研究所,杭州310027;2.浙江省综合信息网技术重点实验室,杭州310027)
实际图像识别场景中样本易受噪声的影响,且大量训练样本的获取比较困难。针对上述问题,提出一种基于混合结构的深度学习网络。选择合适稀疏限制算法运用到自动编码器中,将其构造在混合结构的深度学习网络的底层和高层,解决一般自动编码器无法有效降低背景噪声影响的问题。在深度学习网络的中间层插入改进的无向高斯伯努利受限玻尔兹曼机,进行无监督学习得到低层输出的抽象表示。混合结构的深度学习网络利用最高的回归层进行有监督的微调和分类。实验结果表明,与传统的浅层算法和经典深度学习网络相比,该混合结构的深度网络在大、小样本量的训练下均具有较好的抗噪能力。
混合结构;深度网络;噪声;稀疏限制;小样本量
1 概述
深度学习是一个有效的非监督贪心逐层训练算法,可以有效解决深层结构的机器学习问题,它是近年来该领域的一个重要突破[1-2],理论研究表明,深层结构需要学习很多浅层结构无法完成的复杂函数。它的目标是学习多层次的特征,通过组合低层特征形成更加抽象的高层表示来得到数据的分布式特征表示[3]。相比于传统的神经网络算法,深度学习可以自动从训练集里提取特征而不需要人工干预,并且引入了概率生成模型,解决了容易陷入局部最优值的问题。2种重要的深度结构为深度置信网(Deep Belief Networks,DBN)[4-5]和堆栈自动编码器(Stacked Auto-encoders,SAE)[6]。它们分别由若干受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)和自动编码器堆叠级联而成。这2种结构都可以被用来解决一系列复杂的机器学习难题,并且使得效果有了显著提升。在图像识别问题中,经典的深度学习网络存在着对抗噪声水平较差的不足,尽管后来提出的高斯伯努利受限玻尔兹曼机(GRBM)[7]建模成的无向网络对含噪声的图像有着较好的适应性,但是缺少一种将它结合应用于SAE中的结构。
训练自动编码器要远远较RBM简单,很多研究将自动编码器构建于深度网络的过程中,将它们单独训练以减少运算量。此外,在自动编码器训练过程中,近期提出的大量稀疏限制规则和编码可以提高深度学习的效果[8-9]。稀疏编码的一个重要特征是对外部噪声具有很强的鲁棒性,这对于实际识别的应用场景有着重要意义,因此本文对这一特性做了着重研究。尽管各种结构的深度网络和训练算法被提出来,但是很少有研究将它们各自的抗噪优势结合起来并对实验结果作对比[10-11]。本文将稀疏限制规则引入自动编码器中,对堆叠的自动编码器结构进行拆分,首尾两层编码器之间插入无向GRBM层从而组成混合结构的深度学习网络。在不同强度的噪声影响下与不同大小的训练集下测试整个网络对于分类任务的效果,并与已有的方法进行对比。
2 混合结构的深度学习网络
2.1 自动编码器和GRBM
堆栈自动编码器是使用自动编码器的深度网络的一个变体。自动编码器由编码器和解码器两部分组成,它的目标层输出和可视层输入被限制为严格相等,目的就是为了让输出尽可能复现输入信号。图1为一个自动编码器单元的结构。
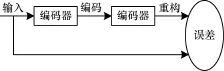
图1 自动编码器结构
编码器和解码器函数如下:

其中,x是输入编码向量;ω1是第1层的权值矩阵;ω2是第2层的权值矩阵;c和b分别是隐藏层和目标层的偏置向量;g()是激活函数,一般为sigmoid()或tanh()函数。
自动编码器的目标函数是最小化重构向量和输入向量之间的最小二乘距离,从而学会如何去重构它的输入:
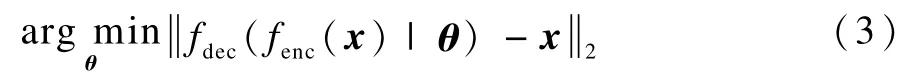
其中,θ={ω1,ω2,c,b}是自动编码器的参数集向量。多个自动编码器堆叠在一起组成的深度网络即为SAE,高层自动编码器的输入来自于下一个隐藏层的输出。与RBM不同,SAE在利用梯度下降法进行训练时,自动编码器的梯度值可以简单精确地被计算出来,并不涉及到像DBN训练中的随机采样过程,计算复杂度较之会大大降低。
GRBM与RBM一样,也是一个基于能量的随机神经网络。它的输入数据由m个可视层单元向量v={v1,v2,…,vm}以及X组隐藏层单元向量h(X)=组成,第x和x+1层之间的权值向量为ω(X),每个隐藏层的偏置向量为b(X),可视层神经元数据的标准差为σi,故GRBM的参数集向量为。与RBM的能量函数E(v,h|θ)=-∑ijωijvihj-∑ibivi-∑jajhj形式类似,对于一个确定状态的GRBM网络,联合组态的能量可以表示为:
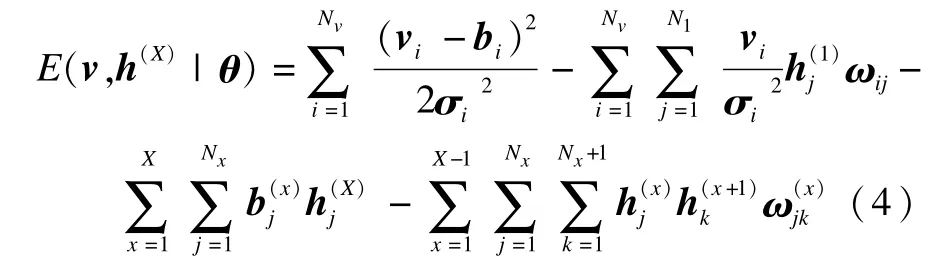
其中,θ是该模型的参数集向量;Nv和Nx分别为可视层和第x层隐藏层的节点数。GRBM中每个节点的(0,1)概率也可以由随机马尔科夫场结合它的联合概率分布来确定:
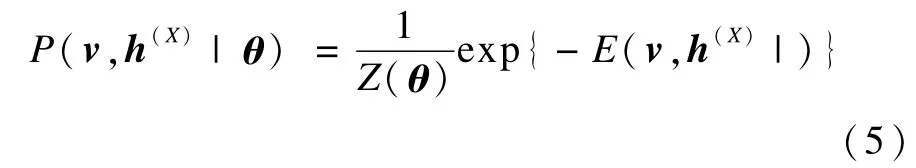
其中,Z(θ)=∑v,h(X)exp{-E(v,h(X)|θ)}作为所有状态能量和的归一化常数被称为配分函数。当相邻层状态给定时,同一层的相邻节点互相独立,可视层的条件概率分布为:
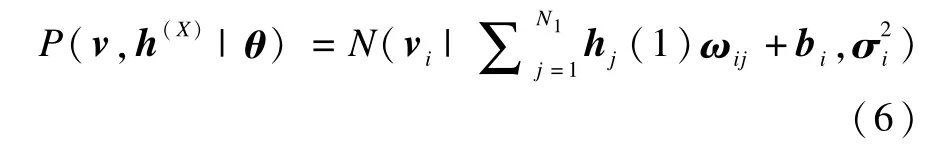
其中,N(~|μ,σ2)表示均值为μ、标准差为σ的正态分布概率密度函数。隐藏层的条件概率分布为:
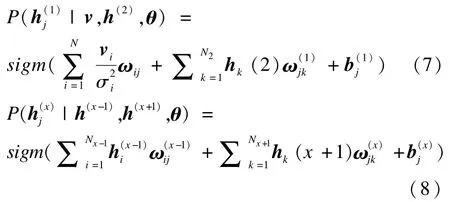
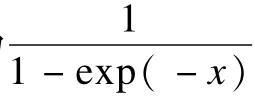
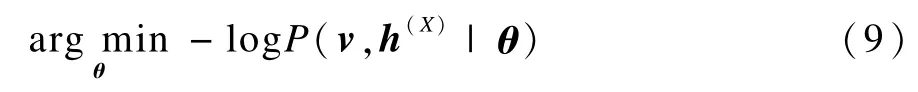
2.2 改进的混合结构深度网络算法
为了实现混合结构的深度学习网络(HybridStructure of Deep Network,HSDN),稀疏限制条件被用于自动编码器,即每一层节点中只有很少的几个非零元素或只有几个远大于零的元素。例如,一张自然图像(高维复杂向量)就可以被表示成少量基本面或线(稀疏向量)的叠加。
把稀疏限制规则应用到自动编码器上,无监督学习算法在与训练过程中的目标函数可被定义为:
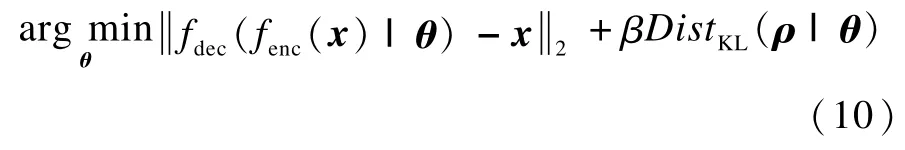
其中,β是规则化常量;ρ是隐藏层的平均激活向量,本文实验选取的DistKL是非标准化的KL散度:
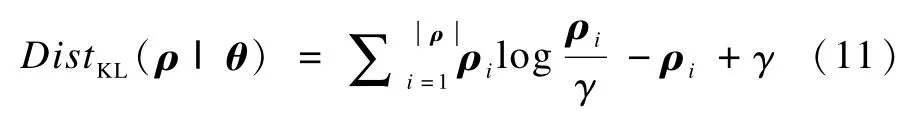
其中,γ是一个接近零值的常量,称作稀疏目标值,常被用来代表隐藏层的平均输出[12]。因此,式(10)的梯度可以推导为:
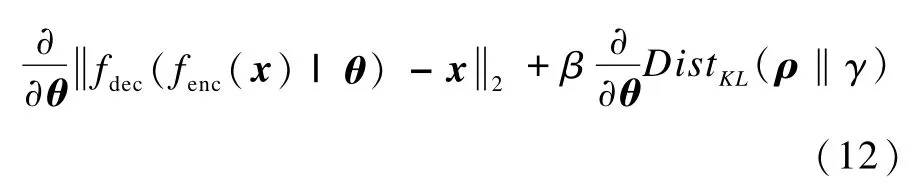
将权值向量ωij和偏置向量c代入θ,得到:
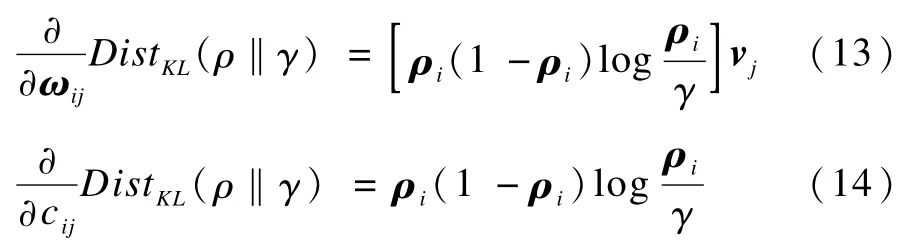
研究表明,对于隐藏层神经元数量大于输入层的情况,稀疏限制的约束条件可以更好地发现输入数据中隐含的信息和结构的表达。
尽管Bengio证明,SAE的训练结果是RBM s的训练结果的近似[13],但是缺少概率生成模型的结构会使得网络的泛化能力不足。在训练自动编码器的过程中,若输入数据源受到较大噪声污染,得到网络参数并不能很好地对抗测试集中随机出现的噪声,从而降低算法的有效性。鉴于求解GRBM参数过程中用到的对比分歧散度算法在Gibbs迭代采样过程中可以很精确地模拟梯度,而天然的概率生成结构可以更有效地应对噪声。SAE的优势在于对于输入信号中有用信息的尽可能的重构和复现,使得信息通过自动编码器后最小化出表现形式变化之外的其他损失,以及训练过程的简化。故本文方法(HSDN)就是将两层稀疏限制的SAE中间插入GRBM结构,利用它们各自的分层判别优势来增大训练网络的边际对数似然估计值。HSDN包括一个底层的稀疏自动编码器,若干个中间GRBM层,以及高层的一个稀疏自动编码器,最顶层使用相应的回归层,具体如图2所示。
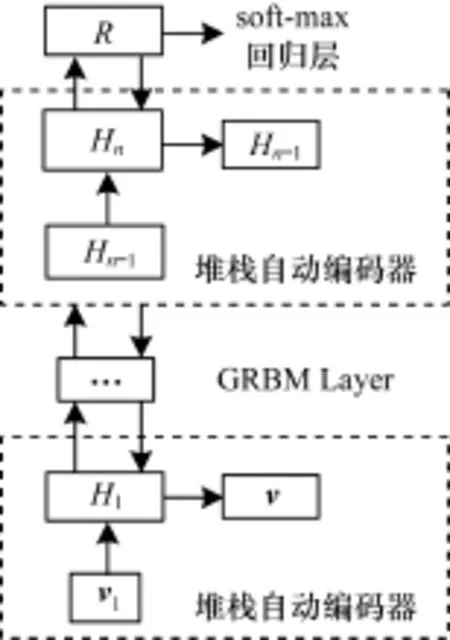
图2 混合结构的深度学习网络
基于上述的混合结构的深度学习将SAE结构隔断,由于各层结构单元的预训练过程都是逐层贪心算法,结构单元的重组并不影响每层训练算法的有效性。与深度学习训练思路类似,HSDN通过一个无监督的贪婪算法逐层去训练获得神经元之间的参数,低层经过训练之后,隐藏层被激活从而作为更高层的输入。在训练过程中,含有噪声的可视层向量v将值传递到隐藏层,然后可视层的输出会被隐藏层随机重建来尝试重构输入向量。文献[15]提出稀疏算法可能导致概率生成系统不稳定,并不适合所有网络层,故在本文结构中的GRBM层并无稀疏性限制,而只限定在自动编码层内。
2.3 网络训练流程
在预训练过程中,最底层的自动编码器将经过预处理的图像像素值当作输入数据,图2中画虚线的稀疏限制自动编码器的部分利用L-BFGS[14]后向传播算法来训练;剩余的GRBM部分利用对比分歧算法进行训练。每个高层的输入数据都来自于更低层,预训练结束后,自动编码器的目标层将不再被使用。最后,通过有监督的训练方法去微调整个网络结构从而更新混合结构的参数和学习到的高层特征。本文实验使用了soft-max回归层来对网络得到的结果进行梯度下降的微调参数和最终分类。尽管第2步~第5步是无监督学习过程,但是最终模型分类还是需要顶层的有监督学习进行微调。
第1步 读取数据集,并进行数据预处理。可选的操作例如基于PCA/ZCA的白化,物理裁剪,归一化等等,根据输入图像的具体情况作决定。
第2步 确定混合深度学习网络各层神经元数量,对网络进行建模。
第3步 每做完一次前向传播计算,通过后向传播算法利用处理过的输入数据对首层的自动编码器进行权值更新。由于存在着稀疏限制,迭代过程中对偏导的求解时应注意改变相应限制项,例如本文计算后使用的系数见式(13)、式(14)。对于底层结构进行重复贪心预训练,直到达到目标函数收敛条件。
第4步 上一步训练得到的隐藏层激活向量直接作为GRBM层的输入进行重构,与经典的对比散度求解相比仅仅多了σ项,具体的迭代采样算法参照文献[7]进行,最终得到的参数会将本层结构的能量最小化。
第5步 将GRBM的输出值作为高层自动编码器的输入,重复第3步的算法,最终可以得到输入向量的一种抽象重构。
第6步 利用10类的soft-m ax回归层进行有监督学习从而微调迭代计算整个网络的预训练参数,得到一个最终网络构造参数向量集合。
3 实验结果与分析
3.1 训练参数和实验设计
设计实验的目的是为了比较本文提出的混合结构算法和非混合的常用深度学习算法以及经典浅层分类方法对于不同程度噪声的识别率的比较。对比实验使用了DBN、无稀疏限制的SAE算法、浅层学习Boost trees(17个分支)算法。
实验测试使用著名的MNIST手写体阿拉伯数字集[16],它包括60 000张图像的训练集和10 000张图像的测试集,在数据预处理时,将灰度图像归一化到[0,1]范围内,由于本文实验目的即为观测算法在不同噪声下的抗噪性能,因此不使用任何其他减噪预处理的方法。
实验硬件环境为Core i7-3770S处理器(3.1 GHz主频)、8 GB内存,利用python和开源的pylearn2项目进行部分深度结构的代码实现。
为简化计算,实验中的深度网络使用的都是相同的结构,HSDN中间层仅使用一个GRBM结构做训练,在各层的神经元数量选择时本文实验与文献[3]的参数一致:即可视层为784个单元(数据库图片统一为28×28像素),第1个隐藏层为2 000个单元,第2个隐藏层为1 000个单元,第3个隐藏层为500个单元,标记层为10个单元。每层结构的学习速率为α=0.1,权值衰减率为λ=0.003。对于网络的自动编码器的稀疏限制训练算法,参数均使用文献[14]值,即β=3,γ=0.1以便作对比,soft-max层微调阶段的梯度下降迭代次数与预训练阶段保持一致。另外,对比实验1、实验2所使用的网络每层神经元个数与HSDN相同。
预训练阶段的每层最大迭代次数是一个重要的参数,迭代次数的选取会影响训练效果速度。随机抽取10 000个训练集样本,迭代次数从10~100以每10次递增进行训练,利用五重交叉验证法对HSDN的分类错误率进行统计,得到的结果如图3所示。由实验结果可知,在迭代次数为50~100之间,最终错误率维持在一个相对稳定的状态,由于增大迭代次数会显著增加网络的训练时间,本文实验中所构建的网络单元最大迭代次数均设为50。
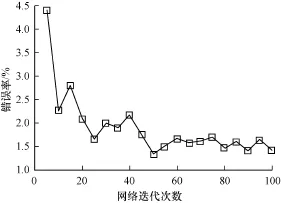
图3 最大迭代次数对分类效果的影响
3.2 结果分析
实验1 在高斯白噪声干扰下进行实验(噪声强度n从10%~60%,实际效果如图4所示)。在不同强度的高斯噪声影响下分别对60 000个训练集中的样本进行训练,同时随机选取测试集里无噪声干扰的5 000张图像作为测试样本,得到相应识别错误率数据见表1。结果显示,训练集在30%强度的高斯噪声影响下,本文的HSDN相比于DBN、SAE和Boost trees在错误率上分别降低了6.94%,4.52%和11.64%。实验数据证明HSDN识别的效果要好于DBN和经典浅层特征的识别算法。特别是随着噪声强度(方差)增加,HSDN抗噪声的能力越来越强,而DBN、SAE结构则介于Boost trees和HSDN之间。

图4 不同噪声及强度下的MNIST样本
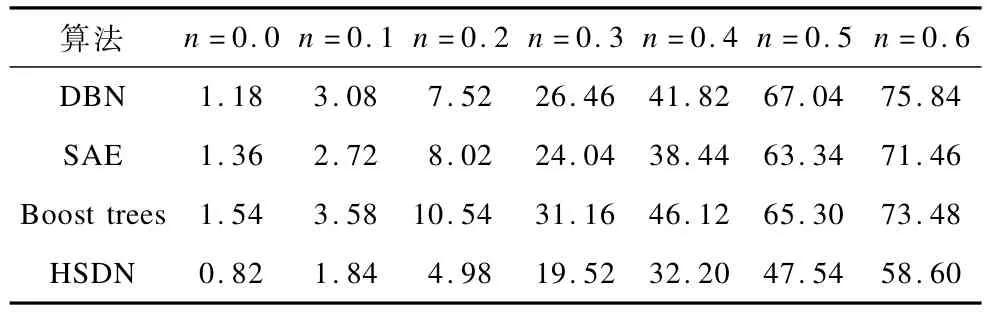
表1 不同噪声强度下分类错误率(60 000张样本)%
从实验结果可以看出,尽管普通的深度学习结构在错误率统计上已经优于浅层学习算法,但HSDN表现出了更好的抗噪性能。这是由于HSDN的底层和高层引入的稀疏限制的自动编码器结构可以当作降噪器,而中间的隐藏层的GRBM结构相当于接受了降噪处理过的输入信号,通过其迭代得到的网络参数能更好地抽象低层的表示向量,防止在出现大量类似噪声的情况下对于网络参数的过拟合。
实验2 不添加噪声干扰时,在训练库的每个数字类别下随机抽取不同数量的训练样本按照对比实验中的相应方法进行训练,得到测试样本的错误率和训练样本数量关系如图5所示。

图5 不同训练样本数量下各算法的分类错误率
实验结果显示HSDN在小样本训练集的情况下始终要优于对比实验结果,并且样本量越小,HSDN与对比实验结果的优势越明显。对于SAE和DBN来说,两者在小样本的训练集下表现出来的效果相近,因为在网络神经元个数相同的情况下2种结构的算法差异本质上仅由于目标函数的不同造成。此外,浅层算法Boost trees在训练样本较小的情况下较深度结构要差,这是由于深度结构是利用无监督的方式自动学习表征样本更加本质的特征,对于训练样本量的需求并没有Boost trees那么大。从这个角度上来说,深层结构更接近于“模拟人脑”而浅层结构更接近于“利用机器分类”。
实验3 为了进一步研究在小样本训练集下HSDN的抗噪性能,实验随机平均每组抽取5 000个训练样本,在不同强度的高斯噪声影响下重复上述方法进行训练,对于不使用噪声干扰的随机5 000张测试样本图像统计识别错误率,结果如表2所示。

表2 不同噪声强度下分类错误率(5 000张样本)%
从实验结果可以看出,在训练样本量减少的情况下,HSDN仍然表现出良好的抗噪能力,错误率均比对应情况下的其他方法要更优,证明了本文HSDN网络结构在不同训练样本量下均具有对噪声较好的鲁棒性。
4 结束语
在构建混合结构的深度学习网络的过程中,本文将有稀疏限制的SAE与GRBM相结合,较大程度提高了算法的抗噪能力,并且实验结果证明该算法错误率低于单纯的DBN网络、SAE网络和浅层学习算法Boost Trees。另外,HSDN在小样本量训练的情况下有着较好的结果。混合结构的深度学习网络对图像原始输入的良好表示和对特征提取方法的不敏感性,适合应用于大量的分类任务。由于现阶段训练速度仍然有限,全面研究在训练过程中不同参数对最终的抗噪能力的影响是下一步的工作。
[1] Bengio Y.Learning Deep Architectures for AI[J].Foundations and Trends in Machine Learning,2009,2(1):1-127.
[2] 刘建伟,刘 媛,罗雄麟.深度学习研究进展[J].计算机应用研究,2014,31(7):1921-1930.
[3] Hinton G E,Salakhutdinov R R.Reducing the Dimensionality of Data w ith Neural Networks[J].Science,2006,313(5786):504-507.
[4] Hinton G,Osindero S,Teh Y W.A Fast Learning Algorithm for Deep Belief Nets[J].Neural Computation,2006,18(7):1527-1554.
[5] Bengio Y,Lamblin P,Popovici D,et al.Greedy Layerwise Training of Deep Networks[J].Advances in Neural Information Processing System s,2007,19(1):153.
[6] Pascal V.Extracting and Composing Robust Features with Denoising Autoencoders[C]//Proceedings of the 25th International Conference on Machine Learning.Helsinki,Finland:IEEE Press,2008:1096-1103.
[7] Cho K H,Raiko T,Ilin A.Gaussian-bernoulli Deep Boltzmann Machine[C]//Proceedings of IJCNN'13. Dallas,USA:IEEE Press,2013:1-7.
[8] 钱 康,霍 宏,方 涛.结合稀疏编码的生物视觉特征提取方法[J].计算机工程,2012,38(13):1-4.
[9] M airal J,Bach F,Ponce J,et al.Online Learning for Matrix Factorization and Sparse Coding[J].The Journal of Machine Learning Research,2010,11(1):19-60.
[10] Bengio Y,Courville A,Vincent P.Representation Learning:A Review and New Perspectives[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(8):1798-1828.
[11] 郑 胤,陈权崎,章毓晋.深度学习及其在目标和行为识别中的新进展[J].中国图象图形学报,2014,19(2):175-184.
[12] Lee H,Ekanadham C,Ng A Y.Sparse Deep Belief Net Model for Visual Area V2[C]//Proceedings of Advances in Neural Information Processing System s. Vancouver,Canada:IEEE Press,2008:873-880.
[13] Bengio Y,Delalleau O.Justifying and Generalizing Contrastive Divergence[J].Neural Computation,2009,21(6):1601-1621.
[14] Ngiam J,Coates A,Lahiri A,et al.On Optimization Methods for Deep Learning[C]//Proceedings of the 28th International Conference on Machine Learning. Bellevue,USA:IEEE Press,2011:265-272.
[15] Xu Huan,Caramanis C,Mannor S.Sparse Algorithms Are not Stable:A No-free-lunch Theorem[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2012,34(1):187-193.
[16] Le Cun Y,Bottou L,Bengio Y,et al.GradientbasedLearning Applied to Document Recognition[J]. Proceedings of the IEEE,1998,86(11):2278-2324.
编辑 索书志
A Research on Anti-noise Per formance of Hybrid Deep Network
WANG Jingyao1,2,LIU Yunhai1,2
(1.Institute of Information and Communication Engineering,Zhejiang University,Hangzhou 310027,China;2.Key Laboratory of Integrate Information Network Technology of Zhejiang Province,Hangzhou 310027,China)
Hybrid structure of deep network which achieves low classification error rate when meeting noisy and limited training data is presented sincemany real world pictures are under noise.Proper sparse regularization algorithm is applied to auto-encoders,which are set on the lower and higher layers and can distinguish background noise more effectively. Middle layer is proposed on the basis of the undirected Gaussian-Bernoulli Restricted Boltzmann Machine(GRBM)to a better abstract representation.Hybrid structure of deep network uses a regression layer on the top for fine-tuning and classification.Experimental results show that hybrid structure of deep network can achieve better performance under noisy background regardless of number of training samples.
hybrid structure;deep network;noise;sparse limit;small sample amount
王璟尧,刘云海.一种混合深度网络的抗噪性能研究[J].计算机工程,2015,41(11):213-217.
英文引用格式:Wang Jingyao,Liu Yunhai.A Research on Anti-noise Performance of Hybrid Deep Network[J]. Computer Engineering,2015,41(11):213-217.
1000-3428(2015)11-0213-05
A
TP18
10.3969/j.issn.1000-3428.2015.11.037
王璟尧(1991-),男,硕士研究生,主研方向:机器学习,图像分析;刘云海,副教授、博士。
2014-11-24
2014-12-17 E-m ail:wang-jy@zju.edu.cn

