基于多体系统理论的数控铣床误差建模
史亚贝 杨 笋
(1.河南工业职业技术学院 河南南阳 473009;2.河南省经济管理学校 河南南阳 473009)
制造业信息化
基于多体系统理论的数控铣床误差建模
史亚贝1杨 笋2
(1.河南工业职业技术学院 河南南阳 473009;2.河南省经济管理学校 河南南阳 473009)
数控机床是机械、钢铁、汽车等行业的主要生产设备,而误差也成为影响数控机床精密度的主要因素。利用多体系统理论来对西门子数控铣床的误差进行建模,通过对误差模型的分析,在安装与制造过程中对误差项进行控制和补偿,从而提高数控铣床的加工精度。
多体系统理论 数控铣床 误差模型
1 多体系统理论
多体系统指多个刚体或柔体部件通过某种方式联结而成的复杂机械系统,是对工程中出现的复杂工程对象的高度概括和抽象。多体系统通过概括和抽象使人更广泛、更深刻地把握事物本质,工程应用中的机械系统都可以通过抽象和提炼成为多体系统。
数控机床是一种典型的多体系统,可以利用多体系统理论来对机床进行误差分析,建立运动模型进行误差补偿,提高加工精度。影响数控机床加工精度的误差主要有形位误差、热变形误差、运动误差、切削力误差及其它误差源。其中几何误差是最根本的误差源,也是形位误差的宏观体现,以西门子数控铣床为例,主要侧重对机床形位误差进行误差建模。
2 拓扑结构
多体系统理论核心是其拓扑结构关联关系的描述和运动学或动力学特征的描述。多体系统误差运动分析的理论基础是多体系统运动学理论,基本原理是用低序体阵列方法描述多体系统拓扑结构的关联关系,用4×4阶齐次方阵描述点和矢量在广义坐标系中的变换关系,使有误差多体系统的运动分析变得简单、迅速、明了和普遍适用。
在画拓扑图时,为每个体编号。编号方法:惯性参考坐标系在床身上,则床身为B1体;沿远离B1的方向按自然数增长从一个分支到另一个分支依次标定所有物体的序号,如图1所示,分别是:1为床身,2为溜板,3为工作台,4为待加工工件,5为主轴箱,6为刀具。根据拓扑结构能够得到误差分支,如图2中的两个误差分支为:1-2-3-4;1-5-6。每个体和序号一一对应,数字大小代表了体的顺序和邻接关系。特征符号描述了相邻体间的运动关系,这样只用序号和特征符号就能将一个复杂机械系统的邻接关系和相邻部件之间的运动关系表示清楚。
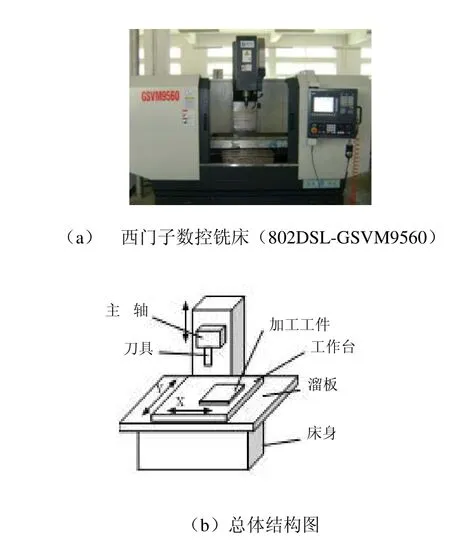
图1 数控铣床及总体结构图示意图
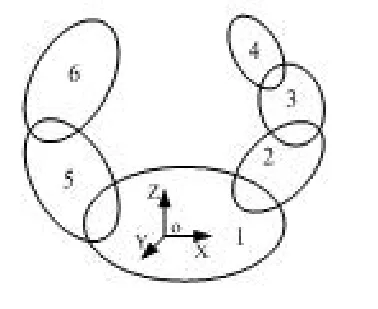
图2 多体系统拓扑结构图
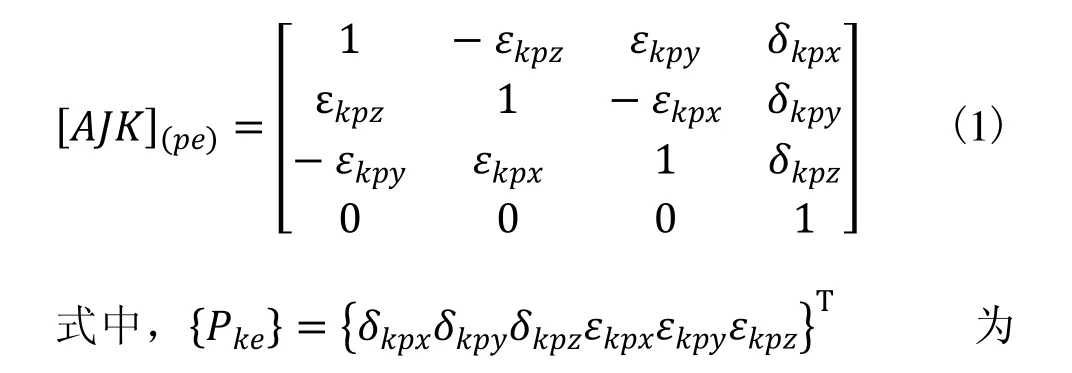
目前,描述多体系统拓扑结构常用方法是运用低序体阵列。用低序阵列描述方法描述多体系统拓扑结构简单、方便,如表1所示,适用于计算机自动描述。
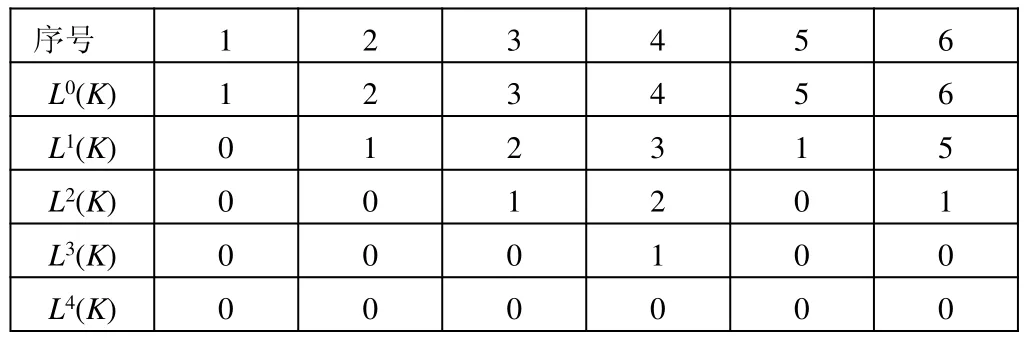
表1 数控铣床多体系统低序体阵列表。
Ln(K)为典型体K的n阶低序体的序号,J为其相邻低序体,则有:
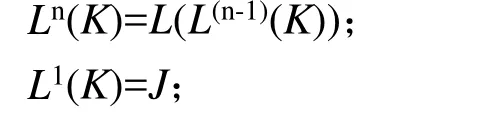
式中:L为低序体算子;N,K为正整数;定义:Ln(k)=K,L0(0)=Ln(0)=0。
相邻体间变换矩阵成为[AJK]′,[AJK]′可用下式表示:[AJK]′=[AJK]p[AJK]pe[AJK]s[AJK]se,式中分别为典型体位置误差和运动误差参考坐标系特征变换矩阵。特殊地,当物体为固定部件时,[AJK]s=[I]。此时,运动参考坐标系和体坐标系重合,变成位置坐标系,相邻体间变换矩阵为位置误差变换矩阵。
3 特征矩阵
相邻体之间的任何运动都是六种基本运动的合成,所以只要知道每一基本运动过程产生的运动误差,就能得知合成运动的运动误差。
下面讨论典型体位置误差和运动误差参考坐标系特征变换矩阵的形成规律。
3.1 位置误差变换矩阵
当位置误差特征为全自由度(六自由度)误差时,位置误差变换矩阵如下式所示。
X、Y轴之间存在垂直度误差,[AJK]pe为:
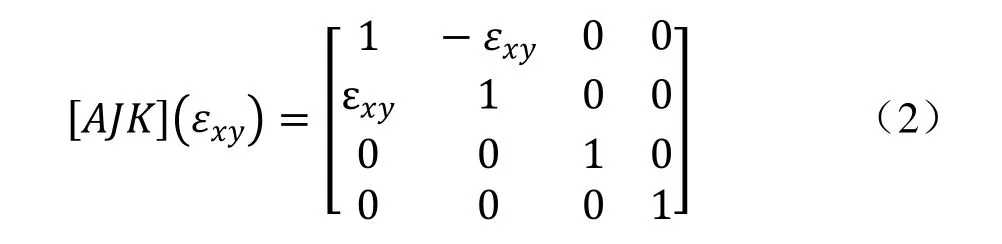
X、Y轴之间存在垂直度误差,[AJK]pe为:
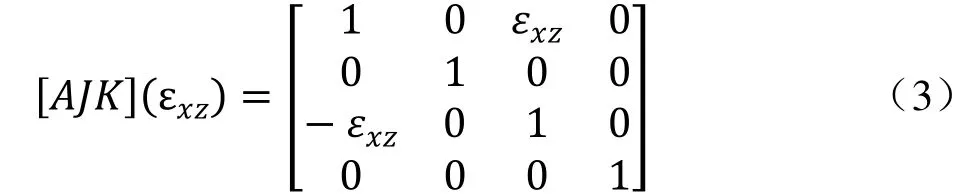
X、Y轴之间存在垂直度误差,[AJK]pe为:
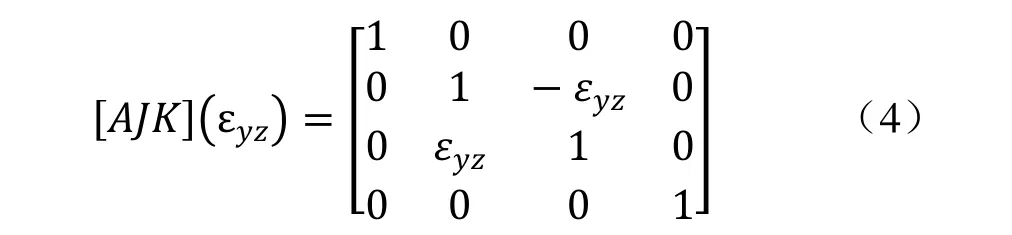
3.2 运动误差变换矩阵
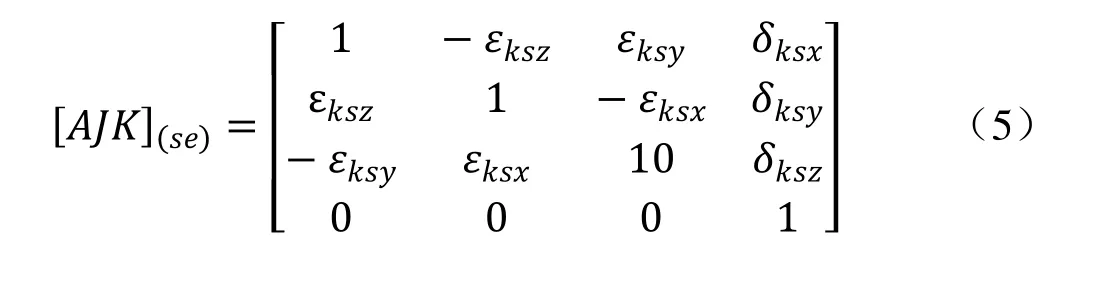
在实际情况下,要首先确定多体系统特征低序体阵列,建立各典型体运动参考坐标系、运动坐标系、位置误差坐标系和运动误差坐标系特征矩阵,即可确定多体系相邻低序体转换矩阵。
4 多体系统相邻体变换矩阵
以数控铣床(西门子802DSL-GSVM9560)为研究对象进行误差建模,其总体结构图和多体系统拓扑结构图如图3所示。
下面根据4×4阶Denavit-Hartenberg变换矩阵列出各相邻体变换矩阵(未写出的为单位矩阵):
4.1 溜板与床身
(1)溜板相对床身沿Y轴移动距离y

(2)溜板相对床身沿Y轴运动产生综合误差
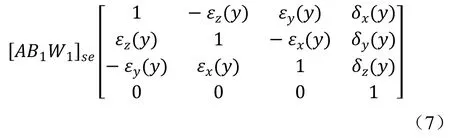
4.2 工作台和溜板
(1)工作台和溜板之间存在垂直度误差

(2)工作台相对溜板沿X轴移动距离X
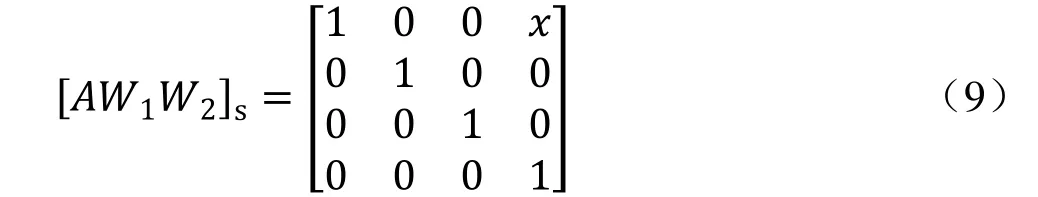
(3)工作台相对溜板沿X轴产生综合误差
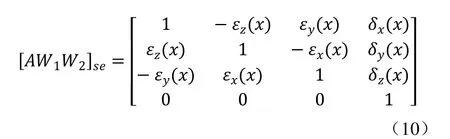
4.3 工件在工作台上的装夹位置,参数取工作台内固定值
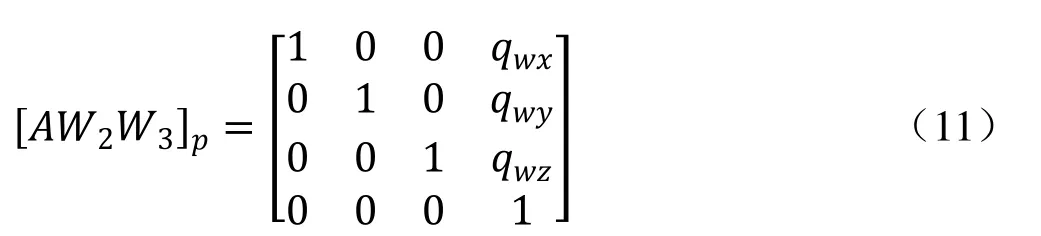
4.4 刀具在主轴箱上的安装位置,参数取主轴上固定值
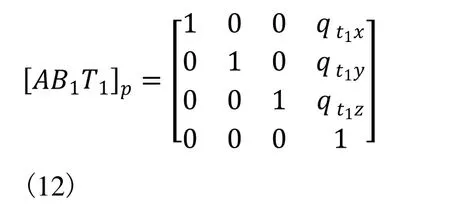
4.5 主轴箱与工作台和溜板之间存在垂直度误差

4.6 主轴箱与床身
(1)主轴箱相对床身沿X轴移动距离z
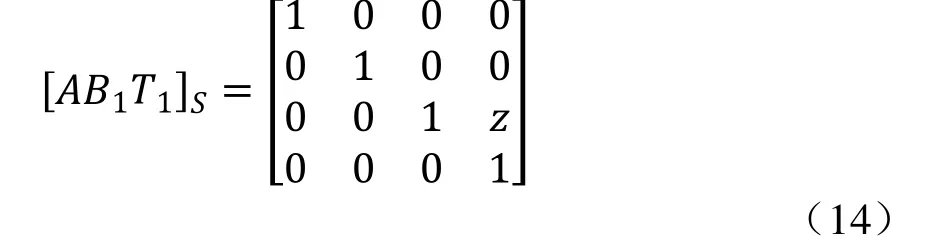
(2)主轴箱相对床身沿Z轴运动产生综合误差

以上在设立数控铣床加工系统中各体的坐标系时,没有考虑载荷变形和热变形对体间位置和位移误差的影响,所以在求取相邻体间变换矩阵时,忽略了大部分由装配引起的位置误差,而其它各项位置和位移误差参数都是空间位置的函数,一经确立,就不再随时间和载荷的变化而变化。
5 结语
多体系统理论具有很强的概括性、通用性和系统性,在航天器、机器人、工程机械等领域得到应用,并在数控机床误差分析、建模和误差补偿的软件实现中显示出其独特的优越性,对数控机床的动态建模方法有显著的理论指导意义及工程实践价值。
[1] 丁晓燕.数控轧辊磨床形位误差分离与补偿研究[D].上海:上海大学,2009,2.
[2] 陈文.基于多学科设计优化理论的数控机床综合误差补偿的并行算法[D].北京:北京工业大学,2009,5.
[3] 张明伟,沈兴全.基于多体系统理论的三轴数控机床误差补偿模型[J].机械工程师,2009(1):111-113.
[4] 谷珂,马闯,吴洪涛.基于多体系统理论的三坐标数控铣床几何误差建模[J].机械制造与研究,2007,36(1):23-24,28.
[5] 林伟青,傅建中等.基于在线最小二乘支持向量机的数控机床热误差建模与补偿[J].计算机集成制造系统,2008(14):295-299.

