优化的粒子群算法在低速永磁直线电机中的应用
朱清智 席东河
(河南工业职业技术学院 河南南阳473000)
优化的粒子群算法在低速永磁直线电机中的应用
朱清智 席东河
(河南工业职业技术学院 河南南阳473000)
系统采用群智能算法对一台功率7.5 kW,效率在75%以上,功率因数在0.8以上的永磁低速直线电机进行了优化改良设计,并对设计结果进行了ANSYS仿真分析,从仿真结果中可以看出提高永磁低速直线电机的性价比,改善电机的电磁性能。
永磁低速直线电机 优化设计 改进的粒子群算法 ANSYS仿真
引言
永磁低速直线电机的结构比普通电机复杂,不同的设计方案对电机的电磁性能会造成很大的影响,且制造成本相差很大,为了保证所设计的永磁低速直线电机具有高效率,高精度,低成本,性能稳定等优点,有必要采用优化方法对现有的低速永磁直线电机进行优化设计,以便获得最佳的效果。
1 永磁低速直线电机原理
根据永磁低速直线电机的结构可以看出,定子和动子都是依靠小齿来释放磁力线的,通过小齿来释放,由于小齿的存在,导致永磁低速直线电机的气隙磁导空间发生了改变。
随着低速永磁直线电机的运动,直线电机定子和动子正对着的位置也将发生变化,在某一时刻定子和动子位置如图1时,其中定子小齿数Z1=12,动子小齿数Z2=14,由图1可知,在该时刻动子小齿1和定子小齿1正对着,则此时该处的气隙磁导最大,同理,动子小齿8和定子小齿7间的气隙磁导也为最大,经过仔细观察不难发现,定子小齿4和10没有动子小齿与其耦合,则此时该处的气隙磁导最小[1]。

图1 小齿和气隙磁导的分布
为了研究的方便,可以像凸极电机那样把气隙磁导最大处定为d轴,把气隙磁导最小处定为q轴,对于永磁低速直线电机来说,小齿产生的气隙磁导在空间的分布是比较复杂的,此处只存在正弦性良好的磁导基波。图2(a)为存在d轴和q轴时的基波磁导分布。个电角度时[2],气隙磁导在空间的分布就如图2(b)所示,则动子移动速度与气隙磁导波移动速度之比可表示为:

图2 基波磁导分布
当动子向右移动3倍的

永磁直线电机行波磁场的同步速为:

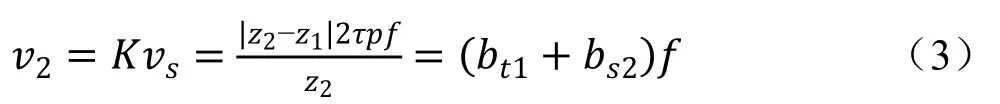
2 粒子群优化算法
在PSO算法中,每个候选解称为一个粒子,若干个粒子就构成了鸟的群体。对于这些粒子来说,没有重量和体积,而是通过目标函数确定它的适应值。每个粒子都通过向自身最好位置和群体当前最好位置不断地学习来动态调整自己的运动方向[3]。假设搜索为N维空间,有M个粒子群,则经过第t次迭代后,第i个粒子当前位置表示为:
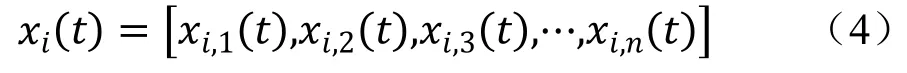
当寻找最小值时,第i个粒子当前位置的更新公式为:

在个体最优位置中,有一个位置能使目标函数取得最优适应值,则称这个位置为全局最好位置,即全局最优(Gbest),一般记为:

在PSO优化控制算法中,速度更新公式:

粒子的位置更新公式为:

其中,i和j的取值范围为:
3 改进PSO算法优化电机
3.1 改进PSO算法
将遗传算法中的交叉应用到PSO中,将粒子的历史最优和全局最优中的某一个对应位置上的元素交叉,提高了粒子的历史最优向群最优的学习能力,增强了算法的寻优能力[4]。
惯性权重的表达式:

其中N为最小惯性权重时迭代次数,t为当前迭代的次数。

位置更新公式

3.2 优化目标函数
将永磁低速直线电机的目标函数定为单台电机的造价与单台电机的电磁推力的比值,则表达式为:
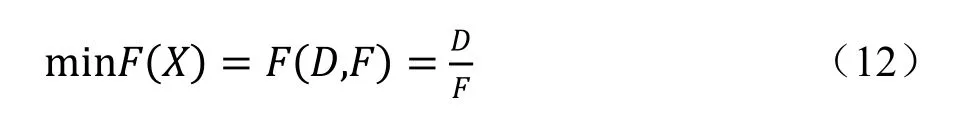
式中X表示优化变量矩阵,D表示单台电机的实际造价,F表示单台电机的电磁推力。
3.3 优化变量
由于目标函数中变量很多,变量间又存在着一定的数学关系,且变量的变化范围差别很大,所以优化变量不容易选取。选择优化变量原则是[6]:
(1)在同等条件下选择变量范围大的变量,且变量范围比较容易确定的作为优化变量。
(2)选取对电机单位长度造价和电磁性能影响明显的变量作为优化变量。
(3)一个设计方案通过选取的一组优化变量确定,并且要尽可能的少的获得一组优化变量。
(4)在一般情况下,选择优化变量应该优先选择连续变化的量。对于不连续的变量,应根据它们分布属性加以规范化处理,使之能满足优化过程中初始点、步长、收敛精度的要求。
4 结语
对目标函数进行优化时,种群数取30,最大迭代次数取1 000,图3和图4为目标函数值随迭代次数变化曲线。

图3 改进前目标函数的输出随迭代次数变化
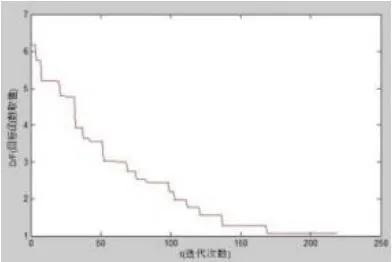
图4 改进后目标函数的输出随迭代次数变化
由图可知,原来的目标函数平均需要223次迭代使目标函数收敛,使用交叉后平均仅需176次迭代就能让目标函数收敛,由此可见,改进的粒子群算法可以提高收敛速度,目标函数在两种优化算法下最终收敛结果相同,论证了改进粒子群算法的正确性。最后,对设计利用ANSYS进行有限元仿真[5]。传统算法设计的永磁低速直线电机仿真结果如图5,6所示。
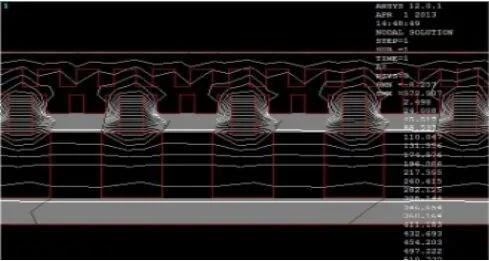
图5 传统方法设计的电机磁力线分布图
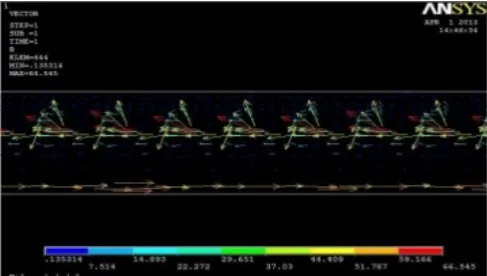
图6 传统方法设计的电机气隙磁密分布图
磁密分布和磁力线经过优化后的分布图如图7,8所示。

图7 优化方法设计的电机磁力线分布

图8 优化方法设计的电机气隙磁密分布
通过对不同结构参数的永磁低速直线电机进行仿真,在电机定子的励磁绕组中通入相同大小的电流密度,发现仿真结果却明显的不一样,优化设计的电机气隙磁密为803,传统设计的电机气隙磁密为644,由此可知气隙磁密提高了24.7%。根据电机的结构参数,可以分别算出电机的造价和电磁力的比值,原来造价与电磁推力的比值为1.53:采用改进PSO算法优化设计的电机造价与电磁推力的比值降低到了1.07,提高和优化电机的性能。
[1] 励庆孚,励鹤鸣.减速式同步电动机的基本理论[J].西安交通大学学报,1977,(01):11-23.
[2] 励庆孚,励鹤鸣.减速式同步电动机的基本理论[J].微特电机,1978,(02):56-68.
[3] 上官璇峰,柳春生,焦留成.永磁低速直线同步电动机研究[J].煤矿自动化,2001,(04):3-6.
[4] 江宏伟.一种新型永磁直线电机动态性能及控制方法的研究[D].武汉:华中科技大学,2008.
[5] 刘细平,刘帅.基于ANSYS的电梯驱动用永磁同步电机磁场有限元分析[J].微电机,2011,(04):16-18.
[6] 周益,刘放,何岚.长定子中低速磁浮直线电机动力学数值分析与优化设计[J].机械设计与制造,2012,(05):36-38.

