基于多元回归数学分析模型某区域内斜坡稳定性研究

周洪燕，李满意，司洪涛

（1.重庆邮电大学移通学院管理工程系，重庆401520；2.重庆地质矿产研究院外生成矿与矿山环境重庆市重点实验室，重庆400042；3.成都理工大学地质灾害防治与地质环境保护国家重点实验室，成都610059）

1 选题背景

中国是亚洲乃至世界上地质灾害最为严重的地区之一，尤以滑坡灾害最为显著，特别是20世纪80年代以来，随着经济建设的高速发展及自然因素的影响，滑坡灾害呈逐年加重趋势；严重的滑坡灾害不仅给当地群众的生命财产造成威胁，还摧毁了相当数量的工矿、交通、水运及水利水电等基础设施的安全运营［1－2］。由于中国的滑坡数量多、发生的频率大、致灾的因素及孕灾的地质条件复杂，加之城区大规模的基础建设，因此，对于区域性滑坡稳定性的评价及发展趋势预测的研究有着重要的社会意义。

关于区域性斜坡稳定性的研究方法比较多，如聚类分析法、信息量法、系统模型法、模糊数学方法［3－4］等。王震宇［5］通过对单体滑坡的多样本分析建立多元非线性回归分析对滑坡的时间预测作了一些尝试，李宏泉［6］把灰色理论和回归分析结合起来对单体滑坡进行了时间预测且有较高的精度。

以西南高烈度山区某县城区域30个滑坡为研究对象，采用多元回归分析的基本原理，研究了区内影响斜坡稳定性的最主要影响因素，采用多元回归数学分析法建立了反映区域斜坡稳定性与各致灾因素的数学分析模型，揭示区域斜坡稳定性与致灾因子的关系，分析和验证该方法的适用性。

2 模型建立原理［7－8］

设致灾因子为确定性变量 （x1，x2，…，xp），随机变量为稳定性y，则多元回归模型为：

式中：β0，β1，…，βp为回归系数；ξ是服从正态分布N（0，σ2）的随机误差。

2.1 回归系数

致灾因子x1，x2，…，xp与随机变量y作随机n组抽样，得到观察值如下：

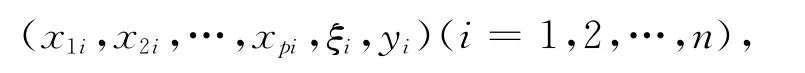
代入式（1）得

式中ξi（i＝1，2，…，n）是服从N（0，σ2）的正态分布的n个独立的随机变量。

设β0，β1，…，βp的估算值为b0，b1，…，bp，则得到多元回归方程

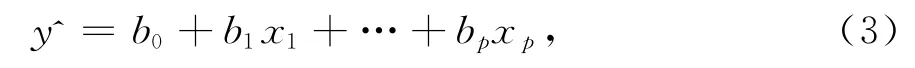
式中y＾为回归方程所给定的数值，即回归值。

yi－y＾刻画了回归值和样本值的偏差，即残值。根据最小二乘法使得残差平方和达到最小即：

采用微积分中的极限值原理，得出b0，b1，…，bp须满足以下条件：

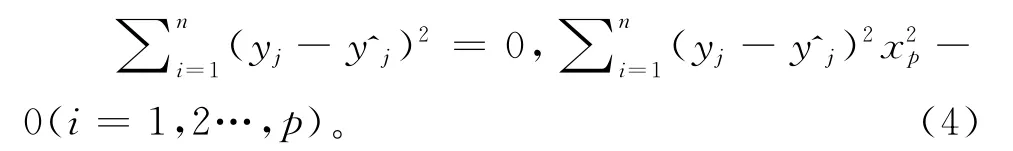
由式（4）可得出

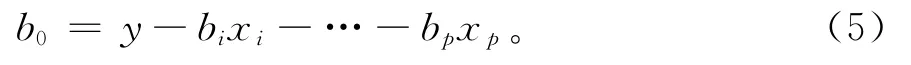
将式（5）代入式（4）解出b0，b1，…，bp，并由式（5）解出b0代入式（3）得到多元回归数学分析模型。

2.2 回归系数的显著性检验

检验回归模型中β0，β1，…，βp是否全为0，即可检验变量间有无联系。若系数全为0，则认为多元回归不显著，反之则回归显著。

假定：H0：βi＝0（i＝1，2，…p），记总的离差平方和为，自由度为f总＝nl总，则Syy可以分解为Syy＝U＋Q。其中：U ＝的自由度y＾j）2的自由度fv＝n－p－1。

做统计量：

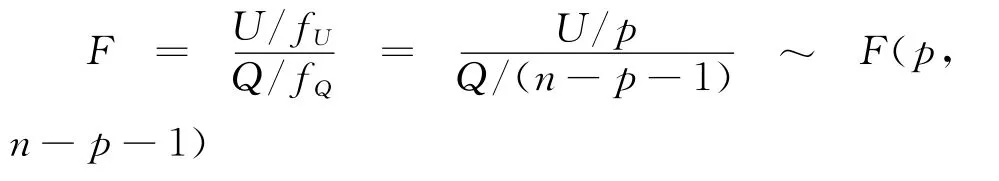
对U的自由度给定检验水平α，查表得Fα（p，n－p－1），如果F＞Fα（p，n－p－1），则因子xi效果显著，否则因子xi效果不显著，去掉因子xi重新建立回归方程。

检验因子xi的显著性等同检验假设：

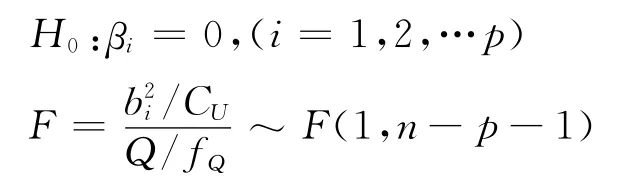
式中Ci是系数矩阵S的逆矩阵S－1的第i行第j列的元素。

对Q的自由度给定检验水平α，查表得Fα（1，n－p－1），若F＞Fα（1，n－p－1），则因子xi效果显著，反之xi效果不显著，需去掉xi重新建立多元回归方程。

2.3 回归方程的预测

3 算例

某县城主要为侵蚀构造中低山地貌，坡度大部分在20°～40°之间，各系地层大致沿构造线向成条带式展布，其中以寒武系邱家河组、第四系全新统沉积分布的地层最广。区内分属3个不同的构造区，北为呈北东向的大断裂，南为呈北东向大断裂，北侧大断裂以北属扬子准地台之摩天岭台隆平；南侧大断裂以南属扬子准地台之龙门山褶断束，构造活动强烈，也处于地震带上，降雨集中，雨量充沛，降雨主要集中在7月—9月，这3个月的降雨量占全年降雨量的50%以上，一般出现在8月上旬或中旬的年最大日降雨量为80～100mm，人类工程活动强烈。

分析该区域典型灾害点的基本特征、致灾因子，进行定性地灾的危险性预测；对各地灾点所处环境、变形破裂特征进行精细描述，对其成因机制分析，宏观判断其稳定性状况，并提出防治建议。

该县城所在的区域是一个地质灾害多发区，尤其是2008年四川汶川大地震，该县城区域因地震诱发的崩、滑等地质灾害造成的经济损失无法计算。为查明该区域地质灾害发生的环境背景，摸清地质灾害的诱发因素，进而确定地质灾害的危险区划，减少因地质灾害造成的经济损失，迫切需要寻求出一套完整的地质灾害危险性评价模型。现对县城区域内5·12地震后的30个滑坡的稳定性进行了多元回归数学分析。在致灾因子xi中选择其中x1，…，x8为自变量，其中x1为斜坡高度，x2为斜坡潜在滑带的强度参数，x3为斜坡坡角，x4为斜坡潜在滑带的平均内摩擦角，x5为斜坡的水文地质条件，x6为区域降雨影响程度，x7为斜坡植被覆盖情况，x8为地震影响程度。自变量x对斜坡稳定性影响大小定量为“1”代表有利，“2”代表不利。因变量y即斜坡稳定性定量为“1”代表稳定，“2”代表基本稳定，“3”代表稳定性差。

对表1中的30个关于斜坡的统计资料进行分析，取掉显著效果不明显的致灾因子，从而建立该区域斜坡的多元线性回归模型，其回归方程为：

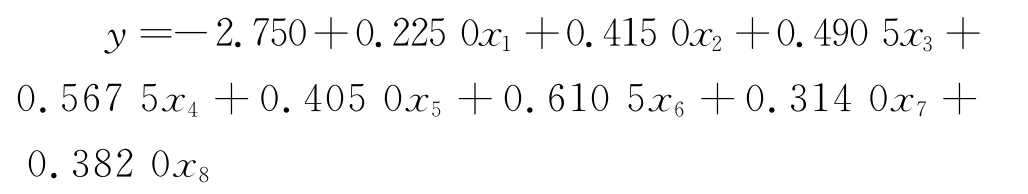
利用回归方程对这30个斜坡进行稳定性预测，其预测结果见表1。从预测效果可以看出回归效果比较明显。从预测结果来看除6＃地质灾害点的回归效果不太理想外，其他斜坡的回归值和原来的分类值相比有较高的贴近度，精度达到了96.7%，模型的回归效果良好，所以在一定的时间范围内可以用来控制和预测。y＾＜1.0时斜坡是稳定的，1.0＜y＾＜2.0时斜坡是基本稳定的，2.0＜y＾＜2.5时斜坡是欠稳定的，2.5＜y＾时斜坡处于不稳定状态。用表1数据对回归方程进行显著性检验，检验结果显示回归效果显著，见表2。

表1 区域斜坡稳定性的多元回归分析

表2 回归方程的显著性检验

4 结语

本文以西南高烈度山区某县城区域内30个滑坡为研究对象，采用多元回归分析的基本原理，研究了区内影响斜坡稳定性的最主要影响因素，采用多元回归数学分析法建立了反映区域斜坡稳定性与各致灾因素的数学分析模型，揭示区域斜坡稳定性与致灾因子的关系。

从多元回归数学分析模型看出斜坡坡角、滑带土内摩擦角、降雨强度及地震成为该区域斜坡失稳的主要影响因素，这也和对当地的客观实际调查情况相符合。该模型的预测结果主要是通过致灾因子的相对性来体现斜坡稳定性的相对属性，这是定量预测的基础。利用此方法对该县城区域斜坡的研究结果表明，得出的回归方程回归效果显著。多元回归分析方法可以用于斜坡稳定性的初步分级，并且方法简单、灵活、成本低，是规划阶段斜坡稳定性评价的有效方法之一。

值得说明的是，滑坡稳定性或失稳具有明显的空间性及地域性特征，须通过野外详细调查，在搞清滑坡的成因机制、失稳机理及合理地确定稳定性影响因素的基础上，才能进行多元回归数学分析。

［1］黄润秋.20世纪以来中国的大型滑坡及其发生机制［J］.岩石力学与工程学报，2007，26（3）：433－454.

［2］罗文强，黄润秋，张倬元.斜坡稳定性概率分析的理论与应用［M］.北京：中国地质大学出版社，2003：1－5.

［3］夏元友.系统加权聚类法及其在滑坡稳定性预测中的应用［J］.自然灾害学报，1997，6（3）：85－90.

［4］徐卫亚，蒋中明，石安池.基于模糊集理论的斜坡稳定性分析［J］.岩土工程学报，2003，25（4）：409－413.

［5］王震宇，孟陆波.滑坡预报的多元回归分析方法［J］.中国地质灾害与防治学报，2003，14（3）：21－23.

［6］李宏泉.灰色理论和回归分析在滑坡预测中的应用［J］.西部探矿工程，2004（11）：212－214.

［7］马还援，宋传中，向钒，等.多元回归分析在安徽省广德县区域边坡稳定性分析中的应用［J］.城市科技，2006，1（2）：43－45.

［8］郭科，龚灏.多元统计方法及应用［M］.成都：电子科技大学出版社，2006：13－18.