浅析渗流场中地下水水力梯度的变化

郎秋玲，刘丽莎

（长春工程学院勘查与测绘学院，长春130021）

0 前言

地下水在渗流场中的运动是复杂的、多变的，且随着含水层透水性能、含水层厚度、隔水底板高程等的变化而发生变化。对于潜水的潜水位，承压水的测压水位，其变化可反映出地下水水头值的变化，而评价其变化的指标可用水力梯度来表示。因而，分析地下水渗流场中水力梯度变化的规律及其影响因素，对研究地下水的运动有着重要意义，本文分析中均不考虑透过包气带的补给及排泄。

1 水力梯度及其影响因素

水力梯度（I）也称为水力坡度，是指沿渗透途径水头损失与渗透途径长度的比值。以潜水面举例，如图1，其中而在实际地下水运动中，潜水面是比较平缓的，因此依据Dupuit假设，假设潜水面水平，等水头面铅直，将水力梯度公式近似计算为此公式也是在研究地下水运动中水力梯度计算时所普遍应用的公式。

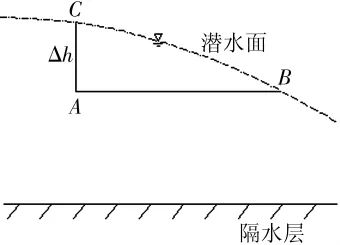
图1 水力梯度示意图

在渗流场中，水力梯度是复杂多变的，其潜水含水层的水力梯度主要随着含水层的厚度、含水层的透水性、地表形状而发生变化，承压含水层的水力梯度主要随着含水层透水性的变化而变化。

2 潜水中水力梯度的变化规律

2.1 潜水面的形状

潜水面的形状随着含水层厚度、透水性能、隔水底板高程的变化而变化。地下渗流场中因地下水运动过程中与固体颗粒间产生能量损失，即水头值下降，当隔水底板水平时，如图2所示，Q＝KhI，h沿渗流途径减小，Q不变，因此沿渗流途径方向，I值增大，即在隔水底板水平，透水性能不变的潜水渗流场中，潜水面为一条上凸的下降曲线，但在实际地下水渗流场中，此变化很微弱。

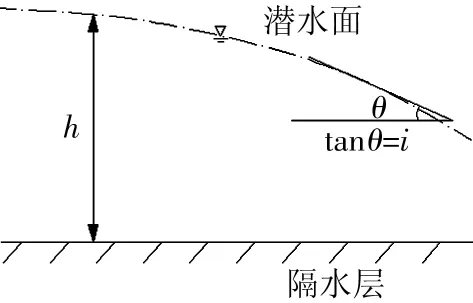
图2 潜水面形状示意图

2.2 与含水层厚度的关系

当含水层厚度突然变大时，如图3所示，根据达西定律Q＝KhI，h1＜h2，Q1＝Q2，K1＝K2，则I1＞I2，表现为潜水面变平缓，水力梯度值变小。

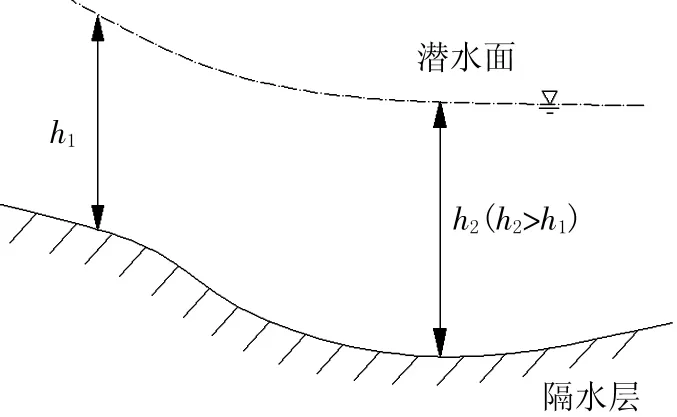
图3 I与含水层厚度的关系示意图

2.3 与含水层透水性的关系

当隔水底板水平，沿渗流途径，含水层透水性能发生变化时，如图4所示，K1≠K2，K越大，地下水运动中能量损失越小，则水力梯度值越小，相反，K越小，地下水运动中能量损失得越多，水力梯度值越大，即当地下水透水性能变好时，潜水面变平缓。

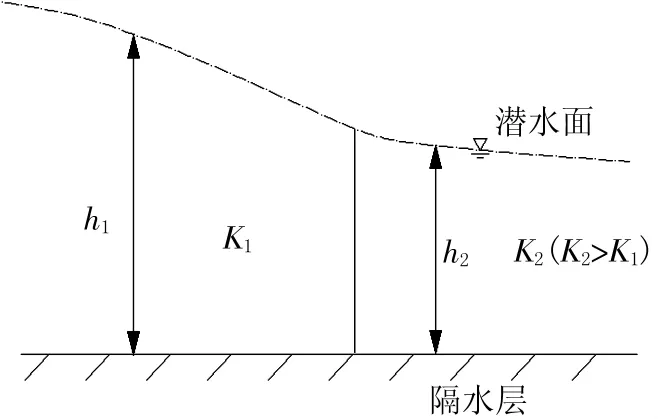
图4 I与含水层透水性关系示意图

3 承压水中水力梯度的变化规律

承压水因往往具有一定的压力值，因此，评价某点处的水力梯度值为该点测压水位的斜率值，假设隔水顶底板水平时的承压含水层，如图5所示，根据达西定律Q＝KMI，Q1＝Q2，M1＝M2＝M，K1＝K2，则I1＝I2，因此，测压水位线为一条斜线，该点上任一点水力梯度值相等。当K发生变化时，K越大，则I越小，即遇强透水层时，测压水位变平缓，水力梯度值变小。

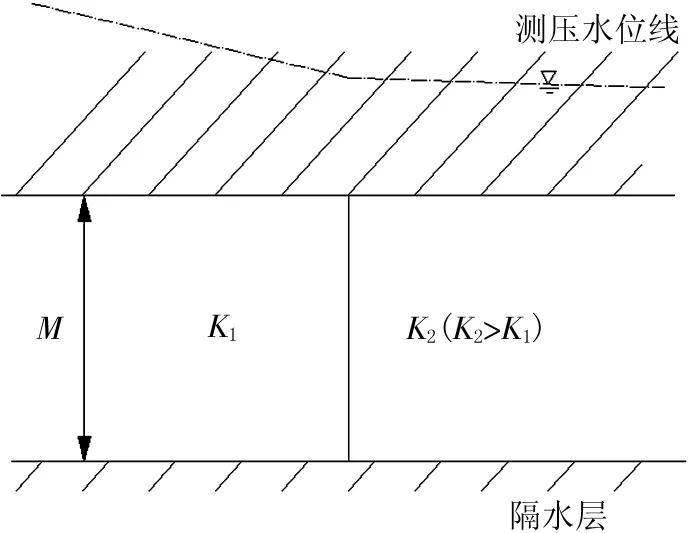
图5 承压含水层水力梯度变化示意图

4 结语

大多数地下水因其运动缓慢，Re较小，符合达西定律，因此，在分析地下水运动规律时，达西定律起到了较为重要的作用。本文分析了水力梯度的变化规律与影响因素，分析总结了水力梯度随含水层厚度、透水性能、地下水类型的变化，潜水位、测压水位的变化与水力梯度的关系，对掌握分析地下水的运动规律有着较为重要的意义。

其主要结论如下：

1）Dupuit假设的前提下潜水面及承压水的测压水位线上任意一点的斜率即为该点的水力梯度。

2）潜水面的形状随着含水层厚度、透水性能、隔水底板高程的变化而变化。

3）含水层厚度突然变大时，潜水面变平缓，水力梯度值变小。

4）含水层透水性能变好时，潜水面变平缓。

5）承压含水层遇强透水层时，测压水位变平缓，水力梯度值变小。

［1］肖长来，梁秀娟，王彪.水文地质学［M］.北京：清华大学出版社，2009：29－34.

［2］代革联.对水力梯度的理解及其应用分析［J］.西北地质，1997（4）：102－105.

［3］宋新江，钱财富.渗流作用下黏性土水力梯度分析［J］.南水北调与水利科技，2010，8（5）：65－68.