基于DtN映射计算周期排列液晶柱的透射/反射光谱

蒋 丹，胡 真

(河海大学理学院，南京 211100)

光子晶体是一种具有周期性的新型人造材料［1］，其最重要的性质是存在光子带隙［2］。频率落在光子带隙的光波不能在光子晶体中传播，从而使得光子晶体具有控制光的能力，被用来设计和制造各种光子晶体元件，在量子信息、超小型激光器、非线性光学等领域发挥了重要作用。

制造光子晶体的材料按性质不同可分为各向同性和各向异性。各向同性材料的性质不会随外界因素变化而变化，由它们制造的光子晶体元件的性能是确定的，不具有可调控性。各向异性材料［3］不同于各向同性材料，其性质受外界因素的影响会发生变化。例如，对各向异性材料施以电流或调整温度等，会引起各向异性材料性质的改变，从而引起由各向异性材料制造的光子晶体结构性能的改变。由此可以通过施加外界影响来实现对各向异性光子晶体元件的调控。

液晶［4］是一种常用的各向异性材料，它的性质随外界条件如电场、温度［5］的变化而变化。近年来，涌现出了大量基于液晶制作的各向异性光子晶体元件，如光调制器、具有记忆效应的元件等。

在模拟和优化设计各向异性光子晶体元件的过程中需要有效的数值方法。传统的数值方法有各种局限性，比如:时域有限差分方法［6］需要很庞大的计算资源，且不容易算出高精度的结果;有限元方法［7］通常需要求解一个很大的方程组，不管是直接求解还是迭代求解都很繁琐。

Xie等在文献［8］中提出:可以利用各向异性光子晶体单元晶格的DtN映射来分析各向异性光子晶体的带隙结构。DtN映射把单元晶格边界上的波动场映射成自己的法向导数。在实际计算中，可以用一个矩阵来近似，这样就避免了计算单元晶格内部的波动场，大大减少了计算量。

本文将利用各向异性光子晶体单元晶格的DtN映射来计算周期排列的液晶柱的透射/反射光谱。这是一个边界值问题，通过利用合适的边界条件截取较小的计算区域，再利用DtN映射进一步减少未知数个数，最终得到一个较小的线性方程组并进行求解。这种方法可用于模拟更多的各向异性光子晶体元件。

1 控制方程

本文研究的是光波在周期排列液晶柱上的透射/反射问题。如图1所示，整个结构是由液晶柱按照正方形晶格排列而成。其中，圆表示周期排列的液晶柱在xy平面上的横截面，整个结构在z方向上没有变化，光波从右侧射入，从左侧射出，共穿过m层液晶柱。

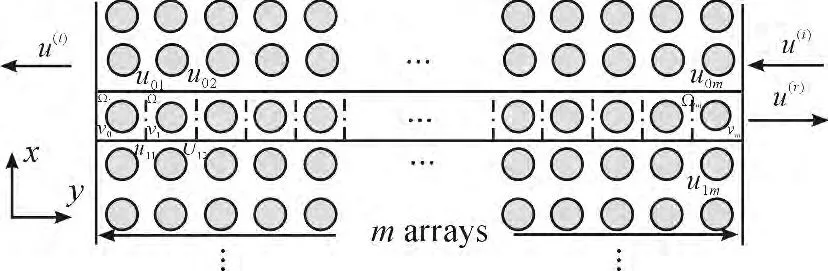
图1 m层周期排列的液晶柱

线性电磁波(光波)在非导电、非磁性、无电流、无电荷的各向异性介质中传播，满足麦克斯韦方程组，考虑时间谐波，对于各向异性的光子晶体，相对电容率可表示成矩阵假设z轴是各向异性介质的一根主轴，相对电容率可写成:

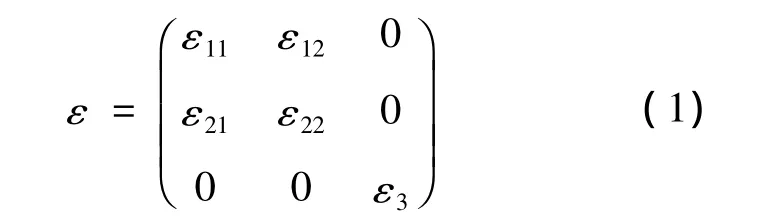
另外，由于图1所示的整个结构在z方向上没有发生变化，此时控制方程可表示为:

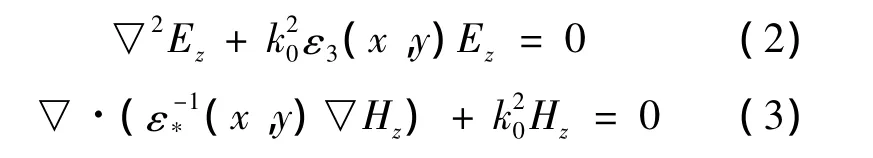
E偏振模式下的控制方程(2)和各项同性介质的控制方程一致，在文献［9］中已有研究。因此，本文只考虑H的偏振情形，控制方程为方程(3)。

2 线性方程组的建立

2.1 边界条件

为了得到较小的计算区域，需要合适的边界条件。图1中实线段围成区域表示结构中的一个周期，也是截取的计算区域。其中:左侧边界上y=0，在y＜0区域中材料的折射率为n1;右侧边界上y=mL，L为晶格常数，在y＞mL区域中材料的折射率为n2。

假设光波从y=mL的右侧区域射入，入射波u(i)和 y轴的夹角是 θ0，可表示为u(i)(x，y)=ei［α0x－β0(y－mL)］，其中:α0=k0n2sin(θ0)，β0=k0n2·cos(θ0)。

反射波u(r)在y＞mL区域可表示为

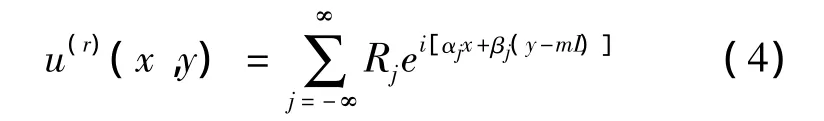
传输波u(t)在y＜0区域可表示为

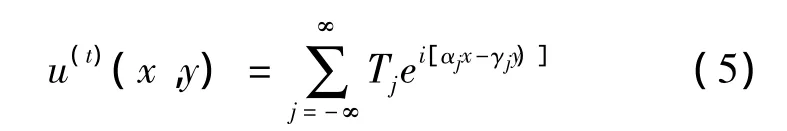
在如图1所示的计算区域外部的4条边界上(实线段)，边界条件的建立过程与文献［9］类似。

在左侧边界(y=0)上，v0，u为控制方程(3)的解，定义算子，使得±2，… ，从而得到边界条件如下:

在右侧边界(y=mL)上，u=u(i)+u(r)。定义算子 s0，使得:s0eiαjx= βjeiαjx，j=0，± 1，± 2，…，从而得到边界条件:

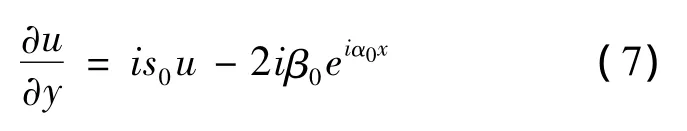
在上侧边界(x=L)和下侧边界(x=0)处，利用结构的周期性，可以得到边界条件:

其中ρ=eiα0L。

2.2 各向异性光子晶体单元晶格的Dirichlet-to-Neumann映射

图1计算区域中的每一个小正方形表示一个单元晶格，半径是a的液晶柱位于正方形中间，正方形边长为L。L也是2个相邻液晶柱中心点之间的距离。

各向异性光子晶体单元晶格的DtN算子的构造过程在文献［8］中已有提及。主要构造过程为:首先对电容率矩阵的子矩阵作对角化，然后旋转、拉伸坐标系，方程(5)可转化为标准的Helmholtz方程:

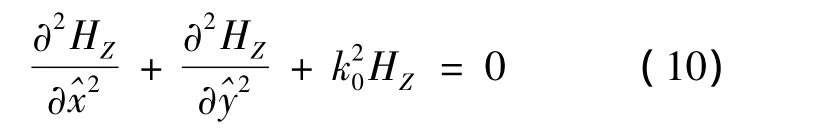
这样，方程(3)的通解为

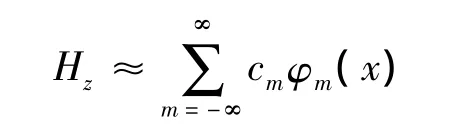
其中:

这里:n0是液晶柱以外的材料的折射率;是待定系数。利用Hz和电场的切向分量在边界面r=a处连续，再利用适当的Fourier展开，可以得到。令u=Hz，Γ为单元晶格Ω

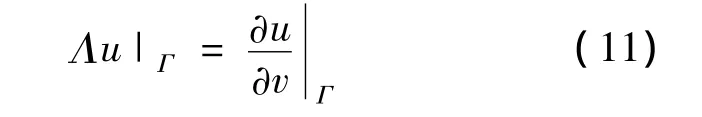
DtN映射Λ将单元晶格边界上的波动场映射成其法向导数，一旦在单元晶格Ω的边界Γ的每条边上离散N个点，DtN映射Λ就可用4N×4N阶矩阵近似。

2.3 线性方程组的建立

在图1所示的计算区域中，利用各向异性光子晶体单元晶格的DtN算子Λ避免了对单元晶格内部的计算，只需计算单元晶格边上的波动场。单元晶格的边分为2类:一类位于计算区域的内部(虚线段);另一类位于计算区域的边界上(实线段)。对计算区域内部单元晶格的边，可用DtN映射建立起关于波动场的方程;对边界上单元晶格的边，可用DtN映射和边界条件建立起关于波动场的方程。

以v1所在的边为例来说明如何对内部边(虚线段)建立方程。由于这条边属于单元晶格Ω1，Ω1的 DtN 映射可表示为:Λ［v0，u01，v1，u11］T=把Λ分为4×4分块矩阵，得到v1法向导数的表达式:

其中u01，v0，u11，v1分别表示 Ω1的上、左、下、右4条边上的波动场。另外，v1所在的边还属于单元晶格Ω2，从而又能利用Ω2的DtN映射得到v1法向导数的一个表达式，而且由于Ω1和Ω2为相同的单元晶格，它们的DtN映射是完全一样的，有的边界，从u|Γ和∂vu|Γ中消去未知系数cm可以得到DtN映射Λ:

其中u02，v1，u12，v2分别表示 Ω2的上、左、下、右 4条边上的波动场。由式(12)、(13)可得到方程:

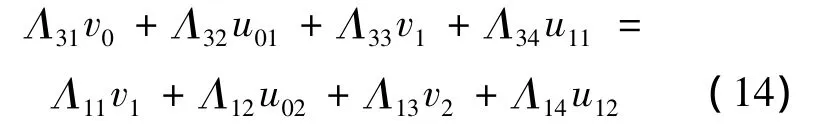
类似地，在计算域内部单元晶格的每条边上(虚线段)都可以建立类似式(14)的方程。

以v0所在的边为例来说明如何对边界上单元晶格的边(实线段)建立方程，在左侧边界(y=0)上，由于这条边位于单元晶格Ω1内，利用Ω1的DtN算子Λ，v0的法向导数可表示为

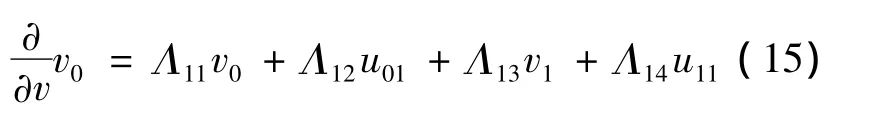
联立式(6)表示的边界条件得到方程:

类似地，对边界上单元晶格的每条边上都可建立类似式(16)的方程。最终，可以得到一个线性方程组:

若单元晶格每条边离散N个点，则系数矩阵A的大小为(3m+1)N×(3m+1)N。

从Ax=b中解出v0和vm(v0是y=0处的波动场，vm是y=mL处的波动场)，利用式(4)、(5)分别求出R0和T0，从而得到透射/反射率。

3 数值算例

当z轴为主轴，各向异性液晶的电容率矩阵可写成矩阵(1)，此时液晶是单轴介质。矩阵(1)有3个特征值，其中2个相等特征值与平凡折射率no有关，另一个不等的特征值与非凡折射率ne有关，液晶的光轴和x轴的夹角用φ表示，则矩阵(1)中的元素可表示为:

为了验证算法的有效性，分别考虑真空中呈周期排列的液晶柱的透射/反射光谱和液晶填充的多孔板的透射/反射光谱2种情况。

首先，模拟光波在真空中呈周期排列的液晶柱中的传播状况。结构如图1所示，圆形表示周期排列的液晶柱，圆外是真空。真空中折射率n0=1;y＜0处的折射率n1=1;y＞mL处的折射率n2=1。光波从右侧射入。参数的选择和文献［8］一致，层数 m=16，半径 a=0.3L，ne=2.223，no=1.590，单元晶格每条边上离散的点数取N=15，光轴与x轴的夹角为，算出透射/反射光谱如

图2(a)、(b)所示。

为了模拟外界因素的变化对光子晶体元件的影响，其他参数保持不变，通过调整光轴与x轴的夹角 φ，取，算出透射/反射光谱，如图2(c)、(d)所示。观察对比透射光谱图2(a)和(c)，发现光的传播情况在0.4附近有明显变化，表现在某些频率的光波由不能在各向异性光子晶体中传播变成可以传播。比如频率为0.391 80的光波，当时，透射率为0.006 6;当时，透射率为0.990 1。而频率为0.392 75的光波，当时，透射率为0.005 7;当时，透射率为0.991 5。

第2个数值算例是模拟光波在液晶填充的多孔板中的传播状况。结构如图1所示，圆形表示用液晶填充的空气洞，圆外是硅板。硅板的折射率n0=3.4;y＜0处的折射率n1=1;y＞mL处的折射率n2=1。光波从右侧射入。层数m=16，半径a=0.4L，L为晶格常数，ne=1.707 2，no=1.529 2，，在单元晶格的每条边上离散19个点，得到透射/反射光谱如图3(a)、(b)所示。

为了模拟外界因素的变化对光子晶体元件的影响，通过调整光轴与x轴的夹角φ，取，计算出透射/反射光谱，如图3(c)、(d)所示，观察对比透射光谱图3(a)和(c)，发现光的传播情况在0.24附近透射率有较大变化，表现在某些频率的波由可以在各向异性光子晶体中传播变成不能传播。比如频率为0.239 80的光波，当时的透射率为0.992 7时的透射率仅为0.000 2;而频率为0.242 45的光波，当时的透射率为0.990 7，而当时的透射率仅为0.003 1。也就是说，施加外界因素影响可以调控特定频率光波的传播情况，使得光波在某些条件下可以传播，在某些条件下不能传播。

图2 φ=和φ=时真空中呈周期排列液晶柱的透射/反射光谱

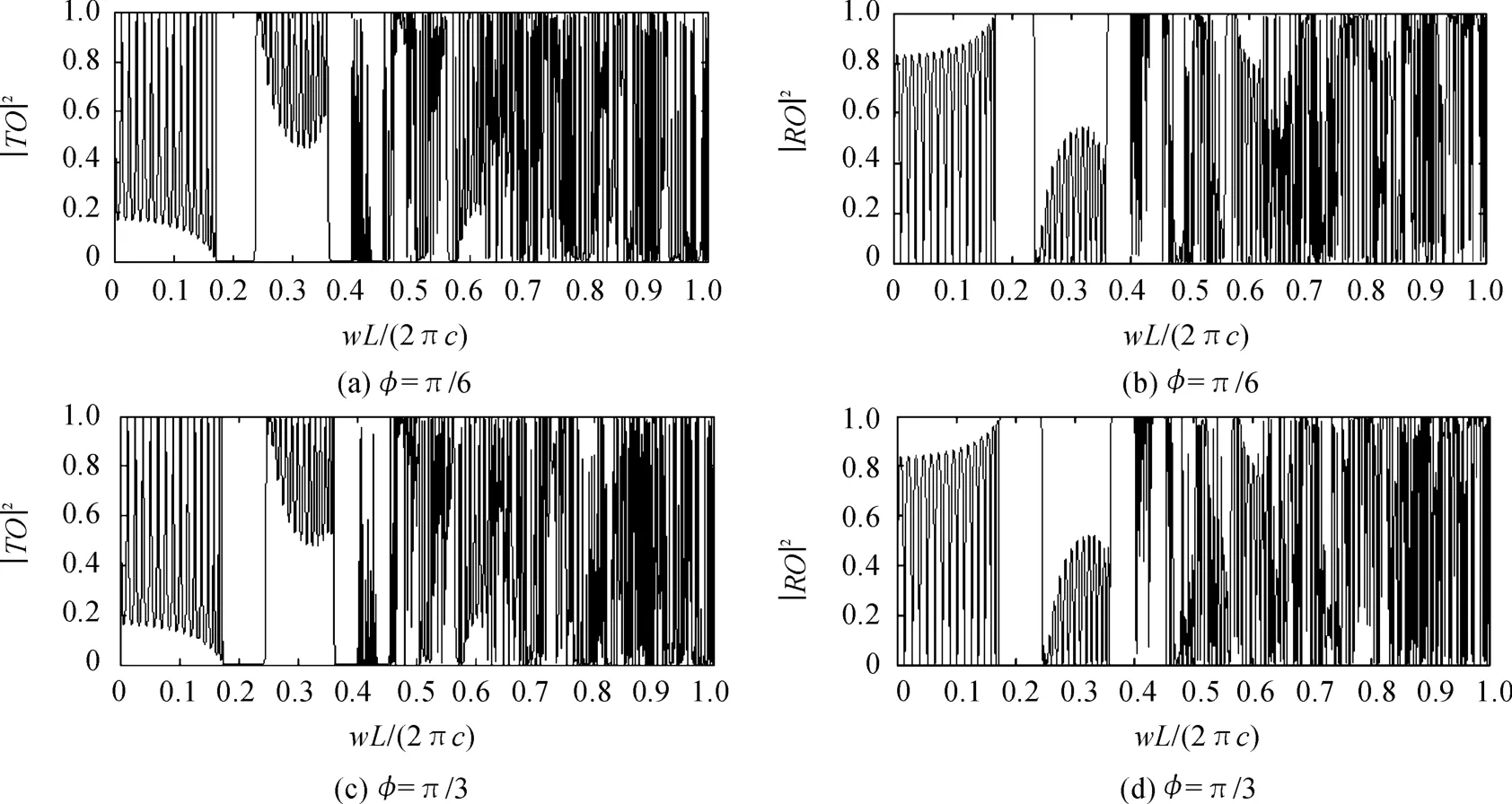
图3 φ=和φ=时液晶填充的多孔板的透射/反射光谱

4 结束语

本文主要研究基于各向异性光子晶体单元晶格的Dirichlet-to-Neumann(DtN)映射，发展了一种能有效分析周期排列液晶柱的透射/反射光谱的数值方法。通过利用DtN算子避免了晶格内部的计算，这样只需计算晶格边界上的波动场，使得未知数的数量大大减少。因此，这是一种快速高效的数值算法，可推广用于模拟各种各向异性光子晶体元件，并进一步用于其优化设计。

［1］JOANNOPOULOS J D，MEADE R D，WINN J N.Photonic Crystals:Modeling the Flow of Light［M］.Princeton，NJ::Princeton Uiversity Press，1995.

［2］龙涛，刘启能.各向异性矩形光子晶体禁带结构及量子效应［J］.激光与红外，2011，41(2):197－201.

［3］慕振峰.各向异性介质波导及含左手材料光子晶体的传输特性［D］.北京:北京工业大学，2013.

［4］FRANCESCA S，SHANE M E，ROBERTO C.Nematic Liquid Crystals Embedded in Cubic Microlattices:Memory Effects and Bistable Pixels［J］.Adv Funct Mater，2013，23(32):3990－3994.

［5］KATSUMI Y，YUKI S，YOSHIAKI K.Temperature tuning of the stop band in transmission spectra of liquid-crystal infiltrated synthetic opal as tunable photonic crystal［J］.Applied PhysicsLetters，1999，75(7):932－936.

［6］SINGH G，TAN E L，CHEN Z N.Efficient Complex Envelope ADI-FDTD Method for the Analysis of Anisotropic Photonic Crystals［J］.IEEE Photonics Technology Letters，2011，24(12):801－803.

［7］CHERBI L，BELLALIA A，UTHMAN M，et al.Modeling of two rings-photonic crystal fibers with the scalar-finite element method［J］.Journal of optoele ctronics and advanced materials，2013(15):1385－1391.

［8］XIE H，LU Y Y.Modeling two-dimensional anisotropic photonic crystals Dirichlet-to-Neuman-n maps［J］.Journal of the optical society of America a-optics image science and vision，2009，26(7):1607－1614.

［9］HUANG Y X，LU Y Y.Scattering from periodic arrays of cylinders by Dirichlet-to-Neumann maps［J］.Journal of lightwave technology，2006，24(9):3448－3453.