基于Sparse ICP的三维点云耳廓识别

王　森， 王　璐， 洪靖惠， 李思慧， 孙晓鹏,2

(1. 辽宁师范大学计算机与信息技术学院计算机系统研究所，辽宁 大连 116081；2. 北京邮电大学智能通信软件与多媒体北京市重点实验室，北京 100876)

基于Sparse ICP的三维点云耳廓识别

王森1， 王璐1， 洪靖惠1， 李思慧1， 孙晓鹏1,2

(1. 辽宁师范大学计算机与信息技术学院计算机系统研究所，辽宁 大连 116081；2. 北京邮电大学智能通信软件与多媒体北京市重点实验室，北京 100876)

提出一种新颖的三维耳廓识别方法，首先基于PCA和SVD分解对三维耳廓点云模型进行归一化预处理，以统一数据库中所有耳廓点云模型的位置与姿态；然后基于 Iannarelli分类系统提取三维耳廓的4个局部特征区域，并利用Sparse ICP算法对局部特征区域进行匹配；最后根据局部特征区域中对应点间的距离判断耳廓之间的差异测度，实现耳廓形状识别。实验证明，本文算法与其他算法相比具有较高的识别精度和识别效率。

耳廓识别；PCA；Iannarelli；局部特征；Sparse ICP

生物特征识别技术有效地避免了传统身份鉴别方式的不足之处，将人体所固有的生物特征数字化、隐性化，更具有普遍性、独特性、永久性和易采集性。

耳廓识别技术是近几年来新兴的生物识别技术，主要利用人耳外形的沟壑曲折等三维形状特征进行识别，同手掌、指纹、虹膜、DNA等人类生物特征一样，是永久性的生物标识。耳廓的三维形状特征不受发型、表情、胡须、化妆、眼镜、肤色、光照等因素的影响[1]，且在7～70岁之间，人类耳廓的结构和外形不会发生明显改变；即便是双胞胎的耳廓也存在可测量的差异[2]；因此与其他人类生物特征相比，耳廓的三维形状特征具有高度的稳定性和唯一性。

1　相关工作

根据不同输入耳廓数据的类型，耳廓识别可以分为二维耳廓识别、三维耳廓识别两种方式。与二维耳廓识别技术相比，三维耳廓姿态受光照等外界因素影响较小，具有显著的健壮性优势。三维耳廓识别一般包括三个步骤：耳廓探测、特征提取以及特征匹配，其中特征提取、特征匹配是三维耳廓识别的核心问题。

1.1三维耳廓特征提取

耳廓由耳轮、对耳轮、耳舟、三角窝、耳屏、对耳屏、耳垂等部分构成，具有显著的起伏外形，具有独特的三维形状特征。2005年，Chen和Bhanu[3]提取三维耳廓模型中耳轮部位的点作为特征点，判断耳轮部分对应点之间的距离，实现了对耳廓的识别。2007年，Chen和Bhanu[4]引入表面的局部曲面片(local surface patch，LSP)方法提取耳廓特征，每个三维点上的 LSP由该点邻域内点集的中心点坐标、该点形状索引对应的形状类型、以及相应的直方图组成，通过比较两个直方图的差异测度判断耳廓特征的相似性；由于待测耳廓之间所有特征点都要进行比较，故识别效率较低。2009年，陈雷蕾等[5]采用两种方式提取耳廓特征，第一种方法将耳廓的深度图像与耳廓的曲率信息相结合，并利用主成分分析(principle component analysis，PCA)降维提取耳廓形状特征，最后利用最近邻分类完成耳廓的识别；第二种方法利用不变特征迭代最近点(iterative closest points using invariant features，ICPIF)算法[6]计算耳廓之间的匹配误差，实现了较好的识别效果。2011年，Islam等[7]随机采样三维耳廓上的点，并对采样点的邻域进行 PCA分析，将第一主轴和第二主轴的长度之差大于指定阈值的点作为关键点，以关键点及其邻域点集的拟合曲面作为特征曲面，实现了耳廓识别。

1.2迭代最近点算法

现有的三维耳廓识别大多基于迭代最近点(iterative closest point，ICP)算法对三维耳廓模型进行匹配。ICP算法通过循环迭代、反复精细调整点云模型的位置及姿态、最小化总体配准误差，从而实现总体最佳匹配。针对ICP算法计算复杂度较高、需要初始对齐等不足，诸多改进的 ICP算法相继提出。

2002年Granger和Pennec[8]提出了EM-ICP算法，省去了初始对齐步骤，直接对变换较大的模型进行配准，解决ICP算法初始对齐的局限性。由于EM-ICP算法较为复杂，计算量较大，2010年Tamaki等[9]提出了基于GPU的EM-ICP算法并对其进行加速；同时引入加权因子解决EM-ICP算法中的噪声值和异常值等问题。2013年 Mohammadzade和Hatzinakos[10]提出新配准方式：迭代最近法向量点(iterative closest normal point，ICNP)算法，其实质是参考模型根据目标模型点集特征的采样，有效找出所有参考模型中具有相同特征的对应点集，即最近法向量点(closest normal points，CNPs)，避免了一些刚性配准算法只适用于几乎不会发生变形的特定区域之间的配准，对于表情变化区域，无法实现准确的配准。然而，利用ICNP算法得到的CNPs不能判断模型间配准质量。同年Bouaziz等[11]提出了一种新的改进方式——稀疏度迭代最近点(sparse iterative closest point，Sparse ICP)算法。利用lp范数取代欧式距离，优化解决最小二乘法问题，降低了异常值和不完整数据对配准的影响，并且采用拉格朗日方法、交换方向乘子法解决非凸性和非平滑性等问题，与启发式方法调整模型间配准相比，如丢弃比较远对应对、除去几何边界上各点等，Sparse ICP算法省略人工交互干涉等繁琐步骤，算法更加可靠。

2　三维耳廓点云预处理

由于三维耳廓数据集构建时间跨距较大，不同的采集时间上获取的同一耳廓数据将受到被采集耳廓与采集设备之间的距离、角度等因素的影响，因此首先需要对三维耳廓数据库中的耳廓模型进行归一化预处理。

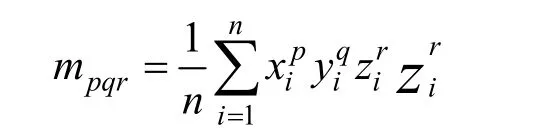
则，V的3个1阶几何矩和6个2阶几何矩分别为：

对于顶点集合V的任意顶点(xi, yi, zi)做如下变换：

设UΔUT=SVD(M)，即对协方差矩阵M进行SVD分解[13]，其中U为矩阵M的特征向量矩阵，对应耳廓模型V的3个主轴，Δ为矩阵M的特征值矩阵，对耳廓模型V的任意顶点(xi, yi, zi)如下变换：

从而使耳廓模型的第一主轴与y轴对齐，第二主轴与x轴对齐，第三主轴与z轴对齐，实现数据库中所有耳廓点云模型均归一化到基本一致的姿态和位置，如图1所示。

图1　三维耳廓点云模型归一化前后对比效果图

3　关键点提取

2010年，Abaza和Ross[14]基于Iannarelli分类系统[15]测量左、右耳廓的几何信息，通过对比左、右耳廓之间几何信息的差异度对耳廓进行识别。图2所示为一个完整的Iannarelli分类系统，该方法基于耳廓的解剖学特征，计算耳廓重要组成部分的相似度，然而在二维图像上各部分尺寸均需要手工测量，无法精确定位。

图2　Iannarelli分类系统

本文基于二维图像空间的 Iannarelli分类系统实现三维空间的耳廓形状特征提取与识别。首先将耳廓模型V的第一主轴与第二主轴作为一对方向，同时将这两个主轴的对角作为另外一对方向，然后沿着这4个方向做法平面与耳廓模型求交，最后提取耳廓中4个局部特征区域对耳廓进行匹配，这4个局部特征区域包含了Iannarelli分类系统中12个重要几何特征(如图3所示)。在人耳数据库中，每个耳廓模型上都提取这样4个局部特征区域，对不同的特征区域进行标号，不同耳廓点云数据模型中，具有相同标号的局部特征区域进行匹配，提高了耳廓模型匹配的精确度。

图3　提取耳廓模型4个子区域

4　Sparse ICP算法

设两个三维耳廓点云模型X和Y分别为参考模型和目标模型，记 X和 Y间的对齐误差向量为zi=Rxi+t−yi，则，记X和Y间的距离为其中并且并记模型间X和Y的误差函数为对齐误差向量的lp范数：

为了进一步优化配准问题，在求解最小化误差函数中，基于拉格朗日方法将对齐误差向量的lp范数重新定义为：

步骤1. 参考模型X与目标模型Y初始对齐，初始化拉格朗日乘λi、惩罚因子μ以及阈值；

步骤2. 对于X的任意点，计算Y上欧式距离该点最近的点，从而得到X和Y之间全部初始匹配点对；

步骤6. 若ϕ(x,y)大于阈值τ，返回到步骤 2，否则迭代结束。

图4为Sparse ICP算法流程，由于引入稀疏度对模型配准优化，并利用 lp范数取代欧式距离，最大化对应点间距离为 0的数量，避免了局部对齐等问题发生。同时，算法采用拉格朗日方法对误差函数重新定义，解决对齐方式造成的模型表面非凸性和非平滑性等问题，并利用交换方向乘子法将重新定义的误差函数分成 3个简单的子问题，并通过收缩算子进行求解，提高了算法的精度和稳定性。

图4　Sparse ICP算法流程

5　实验结果及分析

本文实验在UND三维耳廓数据库上进行，该数据库包含来自415人的1 800幅三维耳廓[18]。本文基于Sparse ICP算法对相同耳廓的不同扫描数据以及不同耳廓的不同扫描数据进行多组实验的匹配，其相关实验结果比较及分析如下。

5.1匹配精度

图5为待测耳廓模型05129d002ear与数据库中耳廓模型Sparse ICP算法匹配后计算的欧式距离平方和相似度分布，其中红色的线表示使用完整耳廓模型进行匹配后的结果，蓝色的线表示使用提取的耳廓区域进行匹配后的结果。从图中可以看出，采用局部区域匹配的耳廓模型精度较高。

图5　采用整个模型与耳廓局域特征区域的精度比较

同样，以05129d002ear为待测耳廓模型，分别于数据库中其他耳廓模型进行匹配，计算模型之间匹配点对之间平均距离，即：

其中，n表示匹配点对的个数；MinDis表示匹配点对之间的距离；i表示匹配点对的序号；k表示区域的序号。显然，DisAvg越小，两个模型相似度越高；DisAvg越大，两个模型相似度越低。平均每个局域的平均距离，即可得到耳廓模型之间的相似度(如表1所示)。显然，Sparse ICP算法与ICP、ICNP算法相比，精度较高，且能够有效区分相同耳廓不同数据的模型。

表1　耳廓间平均距离比较

采 用 累 积 匹 配 特 性 (cumulative match characteristics，CMC)曲线来评估算法的识别效率，其中CMC曲线的横坐标表示在耳廓匹配实验结果匹配最好的前k个的模型，纵坐标表示为三维耳廓识别的正确率。图6将Sparse ICP算法，ICP算法的 CMC曲线进行对比。从该图可以看出，Sparse ICP算法的识别率比 ICP算法的识别率高，其中rank-1达到了93.8%。

图6　CMC曲线

采用接收器操作特性(receiver operating characteristic，ROC)曲线反映正确接受率(genuine acceptance rate，GAR)与错误接受率(false acceptance rate，FAR)的相互关系，GAR表示正确的耳廓被视为正确的百分率，FAR表示错误的耳廓被视为正确的百分率。图7将Sparse ICP算法、ICP算法的ROC曲线进行对比。从该图可以看出，Sparse ICP算法的识别率比ICP算法的识别率高。

图7　ROC曲线

5.2匹配时间

本实验基于2.40 GHz的Intel(R) Xeon(R) CPU，16.0 GB RAM，64位操作系统的计算环境中，对UND三维耳廓数据库中的1 800个三维耳廓模型分别提取耳廓特征区域，并对比了利用完整耳廓模型进行Sparse ICP、ICP、ICNP算法的匹配情况，相应的匹配用时对比如表2所示。可以看出，基于耳廓局部特征区域的匹配用时显然小于基于完整耳廓模型的匹配用时，并且与ICP和ICNP算法相比，Sparse ICP算法时间消耗较少。

表2　匹配时间比较(s)

6　结　论

随着三维模型扫描技术的成熟发展，三维模型的规模快速增长，三维形状特征具有显著的客观性、唯一性，且抗干扰能力强，能够避免二维图像中光照、姿态等因素的影响。三维耳廓模型识别技术，受到越来越多研究者的关注，成为一个新的研究热点。

本文首先采用 PCA算法对模型进行归一化，将所有模型姿态和位置调整一致，然后根据Iannarelli系统提取耳廓模型上的 4个局部特征区域，最后采用Sparse ICP算法对三维点云耳廓子区域进行匹配。实验证明，本文算法与其他算法相比有很高的识别精度和效率。

[1] Prakash S, Gupta P. An efficient ear recognition technique invariant to illumination and pose [J]. Telecommunication Systems, 2013, 52(3): 1435-1448.

[2] Iannarelli A. Ear identification, forensic identification series [M]. California: Fremont Paramount Publishing Company, 1989: 108-119.

[3] Chen H, Bhanu B. Contour matching for 3D ear recognition [C]//Proceedings of Seventh IEEE Workshops on Application of Computer Vision, WACV/MOTIONS 2005, Breckenridge, 2005: 123-128.

[4] Chen H, Bhanu B. Human ear recognition in 3D [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(4): 718-737.

[5] 陈雷蕾, 王斌, 张立明. 快速三维人耳提取与识别[J].计算机辅助设计与图形学学报, 2009, 21(10): 1438-1445.

[6] Sharp G C, Lee S W, Wehe D K. ICP registration using invariant features [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(1): 90-102.

[7] Islam S M S, Davies R, Bennamoun M, et al. Efficient detection and recognition of 3D ears [J]. International Journal of Computer Vision, 2011, 95(1): 52-73.

[8] Granger S, Pennec X. Multi-scale EM-ICP: a fast and robust approach for surface registration [C]//Proceedings of the 7th European Conference on Computer Vision (ECCV) 2002, Copenhagen, 2002: 418-432.

[9] Tamaki T, Abe M, Raytchev B, et al. Softassign and EM-ICP on GPU [C]//Proceedings of the First International Conference on Networking and Computing (ICNC) 2010, Higashi Hiroshima, 2010: 179-183.

[10] Mohammadzade H, Hatzinakos D. Iterative closest normal point for 3D faces recognition [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(2): 381-397.

[11] Bouaziz S, Tagliasacchi A, Pauly M. Sparse iterative closest point [J]. Computer Graphics Forum, 2013, 32(5): 113-123.

[12] Elad M, Tal A, Ar S. Content based retrieval of VRML objects-an iterative and interactive approach [C]// Proceedings of the Eurographics Workshop in Manchester, United Kingdom, 2001: 107-118.

[13] Arun K S, Huang T S, Blostein S D. Least-squares fitting of two 3-D point sets [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1987, 9(5): 698-700.

[14] Abaza A, Ross A. Towards understanding the symmetry of human ears: a biometric perspective [C]//Proceedings of 2010 4th IEEE International Conference on Biometrics: Theory Applications and Systems (BTAS), Washington DC, 2010: 1-7.

[15] Prakash S, Gupta P. An efficient ear recognition technique invariant to illumination and pose [J]. Telecommunication Systems, 2013, 52(3): 1435-1448.

[16] Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers [J]. Foundations and Trends in Machine Learning, 2010, 3(1): 1-122.

[17] Parikh N, Boyd S. Proximal algorithms [J]. Foundations and Trends in Optimization, 2013, 1(3): 123-231.

[18] Yan Ping, Bowyer K W, Biometric recognition using three-dimensional ear shape [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(8): 1297-1308.

3D Ear Point Clouds Recognition Using Sparse ICP

Wang Sen1,Wang Lu1,Hong Jinghui1,Li Sihui1,Sun Xiaopeng1,2
(1. Computer System Institute, Department of Computer and Information Technology, Liaoning Normal University, Dalian Liaoning 116081, China; 2. Key Laboratory of Intelligent Telecommunications Software and Multimedia, Beijing University of Posts and Telecommunications, Beijing 100876, China)

A novel 3D ear recognition method is proposed in this paper. Firstly, using the PCA and SVD algorithm to normalize 3D ear point clouds model, and adjust the position and posture of all ear point cloud models in the database. Then, based on the Iannarelli system, we extract four local feature regions of 3D ear model, and match them with Sparse ICP algorithm. Finally we match 3D ear models according to the distance between their corresponding points. The experiments show that our algorithm has higher recognition accuracy and efficiency compared with other algorithms.

ear recognition; PCA; Iannarelli; local feature; Sparse ICP

TP 391

A

2095-302X(2015)06-0862-06

2015-06-24；定稿日期：2015-07-08

国家自然科学基金资助项目(60873110，61170143，61472170)，智能通信软件与多媒体北京市重点实验室开发课题(ITSM201301)

王森(1992–)，女，辽宁大连人，硕士研究生。主要研究方向为计算机图形学。E-mail：cadcg2008@gmail.com

孙晓鹏(1968–)，男，辽宁大连人，教授，博士。主要研究方向为计算机图形学。E-mail：xpsun2008@gmail.com