基于补偿方法的高超声速滑翔飞行器多变量输出解耦控制

杜立夫 黄万伟 杨广慧 禹春梅

北京航天自动控制研究所，北京100854

临近空间高超声速飞行器一般是指飞行马赫数大于5 的飞行器，而高超声速滑翔飞行器是利用高升阻比的特殊气动外形，使其能利用空气动力在大气层和跨大气层中实现高超声速远距离滑翔机动的飞行器。高升阻比的气动外形使得主升力面在俯仰通道上，这样俯仰通道的机动能力很强，偏航通道的机动能力很弱，此时采用BTT 控制进行横向机动来满足飞行任务的需求，飞行器快速的滚转导致俯仰、偏航和滚动通道存在强烈的运动学、惯性和气动力耦合效应，如果直接应用STT(侧滑转弯)控制，这种在工程上广泛使用的三通道独立控制系统设计方案，那么其交连耦合将使滑翔飞行器在倾斜转弯时容易诱发较大的侧向过载和侧滑角，侧滑通道会受到较大的干扰，想要控制较小的侧滑角比较困难，不能满足BTT 控制对侧滑角较小的要求，滑翔飞行器长时间飞行很可能失稳失控，必须消除或减小三通道之间的交连耦合作用，因此需要对滑翔飞行器进行多变量系统设计，这样才能保证侧滑角满足要求［1］。

本文利用飞行器的BTT 控制技术，首先采用三通道独立设计，然后加入协调控制支路进行补偿解耦，其中三通道独立设计采用自适应PID 方法，控制器参数随飞行高度和速度的变化而变化。在对系统交连耦合程度分析的基础上提出了按交连耦合项系数大小进行补偿的方法，并以此设计了变增益的协调控制支路来补偿系统的交连耦合［2］。最后通过高超声速滑翔飞行器的三自由度非线性仿真对控制方案和控制参数进行检验。

1 高超声速滑翔飞行器多变量耦合系统模型

BTT 控制的高超声速滑翔飞行器(以下简称滑翔飞行器)的控制系统设计目标是:俯仰通道、滚转通道跟踪攻角、速度倾斜角指令，偏航通道侧滑角的控制指令为0，即α→α0，γv→γv0，β →0 。控制系统运动耦合是BTT 控制所固有的，这种耦合不能当作一般意义上的系统干扰对待，因为它是系统运动状态的函数，具有与系统模态同样的动态行为，所以这种BTT 控制设计对象是一个多变量耦合系统，对高超声速滑翔飞行器非线性运动方程进行线性化，在标称条件下，得到多变量控制系统的状态方程如式(1):

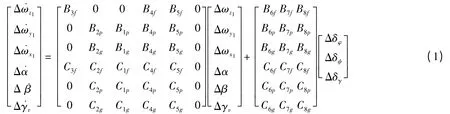
其中，ωz1，ωy1，ωx1分别为俯仰、偏航、滚转转动角速率;α 为攻角，β 为侧滑角，γv为速度倾斜角;B，C 为小偏差方程动力学系数。

2 三通道控制回路独立设计

2.1 三通道独立回路自适应PID 控制方案

三通道独立就是不考虑系统俯仰、偏航和滚转3个通道之间的任何交连作用，每个通道单独考虑，进行控制器设计。线性化方程组是变系数的线性微分方程组，方程组中的各个系数(如B3f，B4f，C4f，B6f，C6f)均是时间的函数，随飞行高度、速度、攻角、侧滑角和舵摆角的变化而变化。以俯仰通道为例，在上述飞行高度和速度范围内，根据计算，俯仰控制通道的参数B3f，B4f，C4f，B6f，C6f的变化范围如表1 所示。

表1 俯仰通道系数的变化范围

可以看出，系统的系数变化范围很大，为了能适应参数的大范围变化，3个通道均采用参数自适应PID 控制［3］，其控制方案如式(2):

式(2)中，控制参数的第1个下标用来区分比例、微分和积分控制，分别对应于p，d，i;第2个下标用来区分通道:f 表示俯仰通道;p 表示偏航通道;g 表示滚转通道。

2.2 三通道独立回路控制系统设计

现在以滑翔飞行器某具体状态为例进行设计，选择的状态如下:

作用在滑翔飞行器上的力矩随时处于“配平状态”，得到配平状态的系统舵摆角为

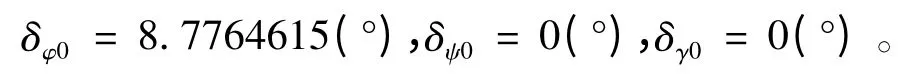
采用PID 方法进行控制器设计，经过反复调整得到控制参数如下:

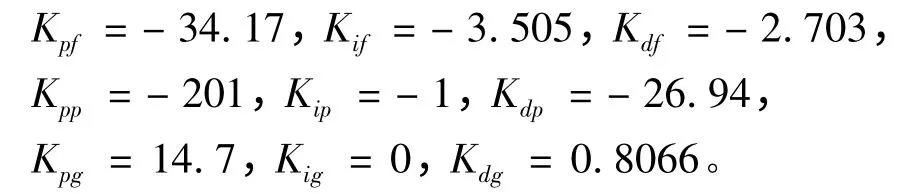
根据平衡状态点的动力学系数，可得系统三通道的开环传递函数如下式:

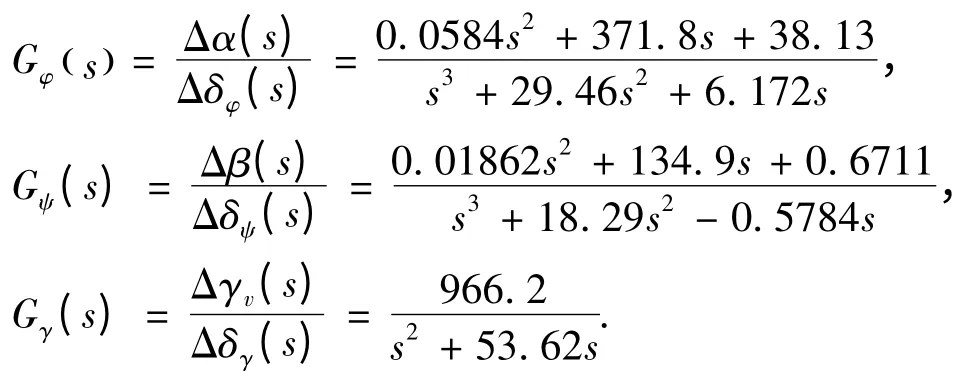
通过开环传递函数容易得到三通道的频域波特图，如图1 ～3 所示。

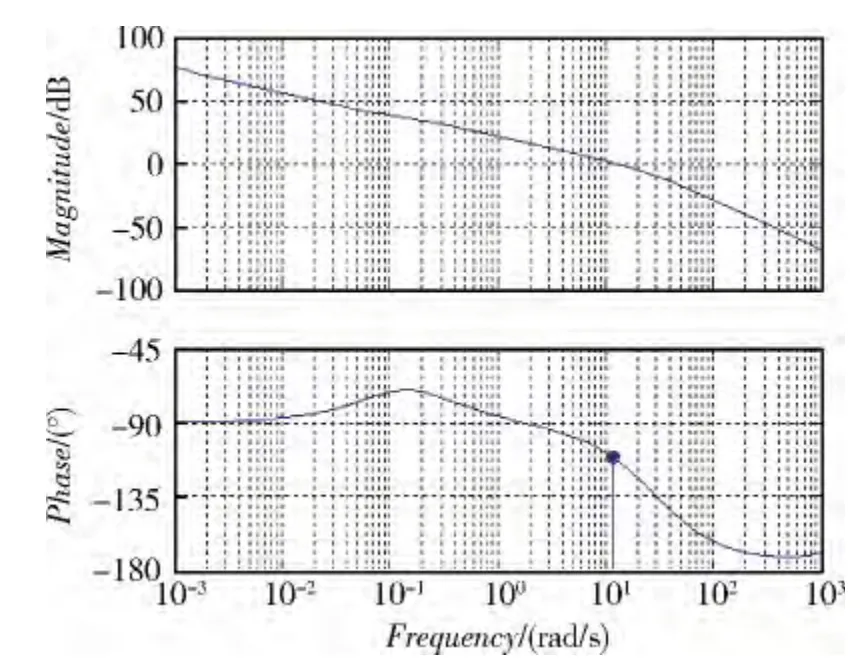
图1 俯仰通道波特图

由对数频率稳定判据可以判定三通道系统均为稳定的，控制系统有较好的稳定裕度，但这样的结果是在不考虑系统各通道交连耦合影响的情况下得到的，实际情况是各通道存在比较大的交连耦合，因此必须对系统进行解耦设计。

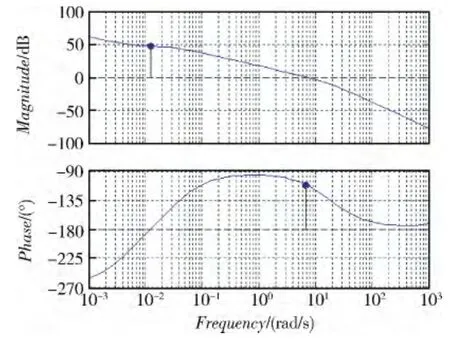
图2 偏航通道波特图

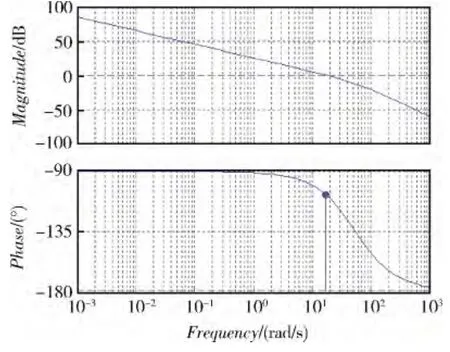
图3 滚转通道波特图

3 滑翔飞行器三通道耦合分析与解耦补偿设计

单通道控制器对单通道被控对象有很好的效果，但是这里没有考虑三通道之间的交连耦合作用，实际情况是偏航通道受到滚转通道较大的干扰，不能保证侧滑角较小的要求。因此，在此基础上，需要对系统做进一步设计。

3.1 三通道交连耦合分析

现在仍以滑翔飞行器的平衡状态点Ma0= 20，h0= 50(km)，α0= 8.5(°)，β0= 0(°)为例说明滑翔飞行器三通道之间在此刻的交连耦合情况。综合上面3个通道单独设计的结果，可得图4 滑翔飞行器的三通道交连结构图。

由图4 可以看出，俯仰、偏航和滚转3个通道的控制器和反馈回路不涉及系统的交连耦合，在只考虑系统耦合时可以不予考虑控制参数的变化。

以Δδ'φ，Δδ'ψ，Δδ'γ为输入，Δα，Δβ，Δγ 为输出的系统传递函数矩阵为G' ，它包含了系统所有的交连耦合，见图5。

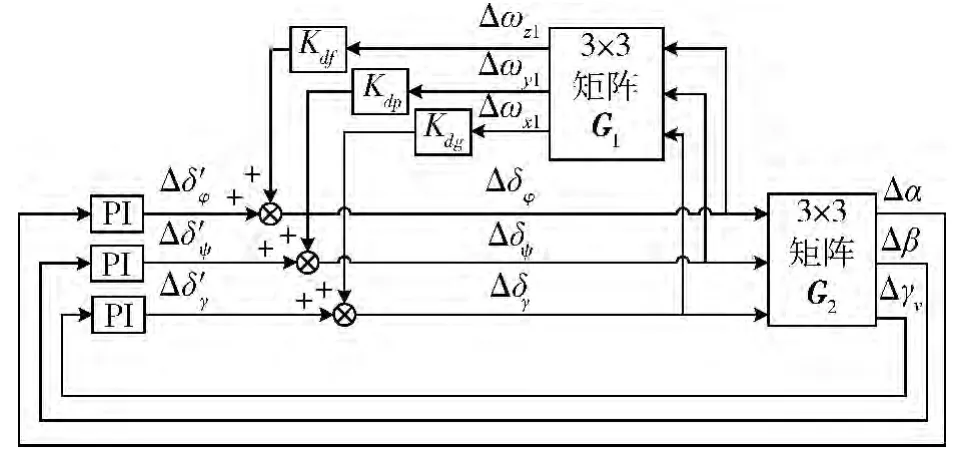
图4 滑翔飞行器三通道交连耦合结构图

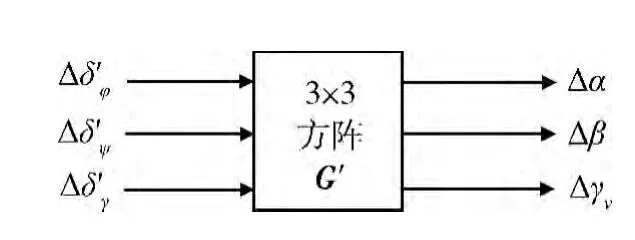
图5 滑翔飞行器的三通道简化交连结构图

由图4 可解得矩阵G' 为:

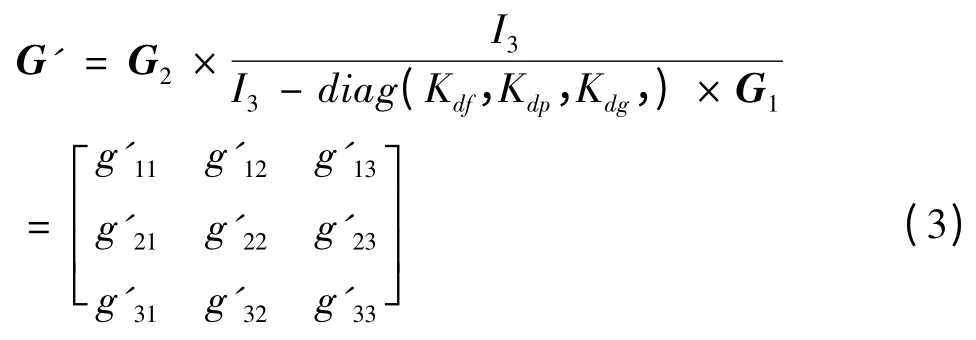
其中，取三通道PID 控制器的微分控制参数为Kdf= －2.703，Kdp= －26.94，Kdg= 0.8066 。根据平衡点的气动数据可计算得到线性交连模型的各个系数，因此只要知道它的对角优势程度，就可以知道系统的交连耦合程度［4］。按矩阵对角优势度的定义，令s = jω，然后按照频率可以画出矩阵G' 在一定频率范围的对角优势度如图6。

由图6 可以看出，矩阵G'的第1 和3 行具有行对角优势，第2 行不具有行对角优势，即弹头的三通道之间，俯仰、滚转通道可认为是独立的，受到其他通道的干扰比较小，而偏航通道则受其他通道的干扰较大，须进行补偿，加入协调控制支路，以减小干扰。

3.2 补偿解耦设计

滑翔飞行器三通道之间，只有偏航通道受到其他通道的干扰较大，需要进行协调控制，其他2个通道受到的干扰较小，可以忽略，不需要设计协调控制支路。引入ωx1α 和ωx1β 作为协调支路，从理论上讲，增加2 条这样的支路，极性与对应支路的极性取相反，就可达到解耦的目的。但是由于交叉耦合在系统内部，因此，这样的补偿物理上不可实现，设计协调控制支路在工程上就是把协调支路移到弹头舵机的输入端，通过调整协调控制支路的增益，完全可以达到减小系统交叉耦合的目的。

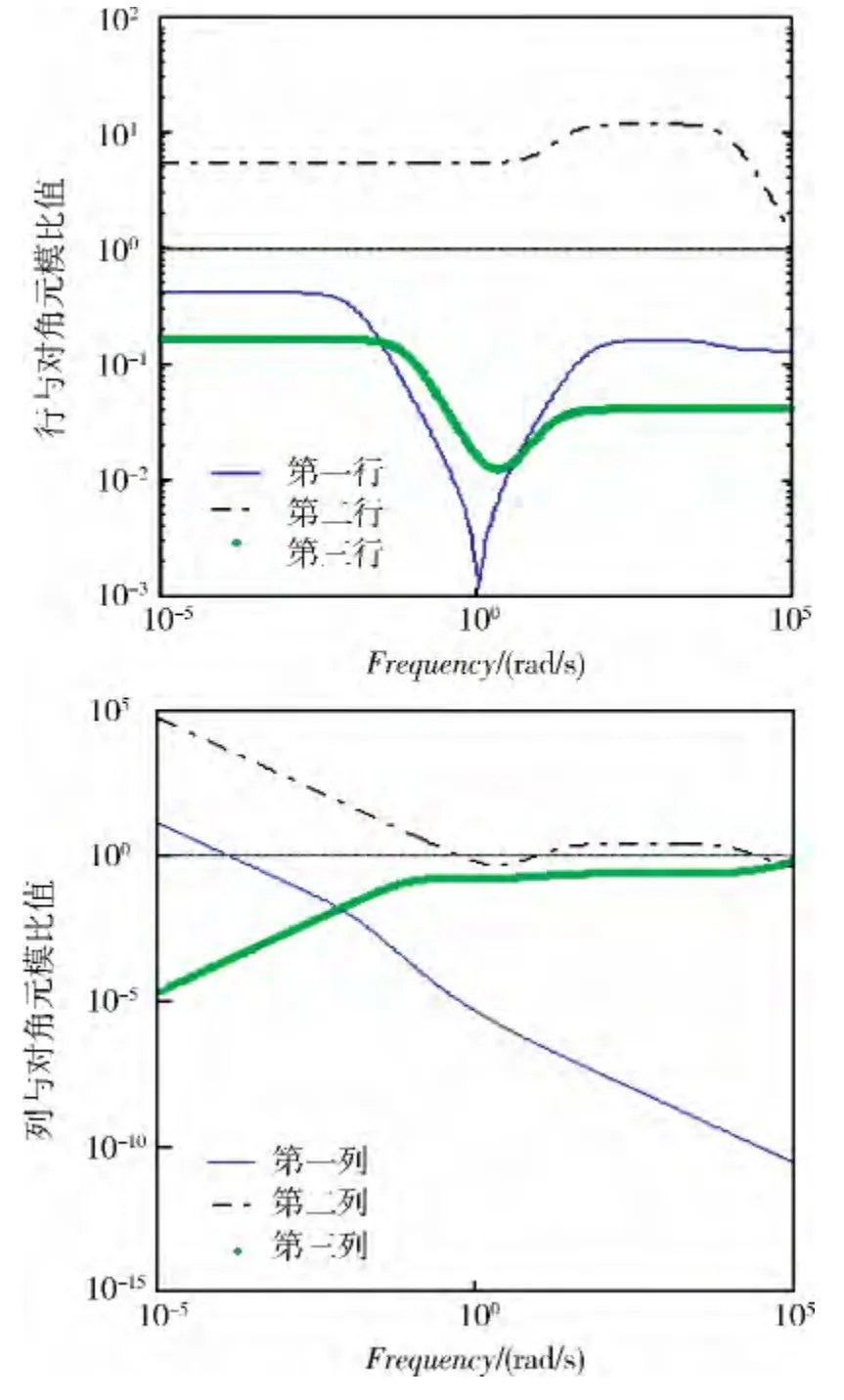
图6 三通道独立控制的交连耦合系统对角优势度图

对偏航通道设计2 条协调支路进行补偿解耦，如图7 所示，分别为:

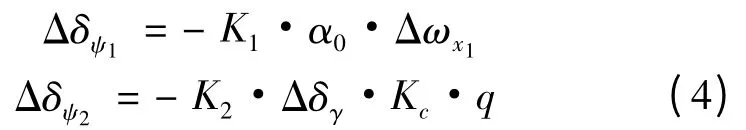
其中，Kc= －0.000163 ，为常数。K1，K2根据系统的状态进行设计，因为滑翔飞行器在整个滑翔过程中参数变化较大，因此同三通道的控制系数Kp，Ki，Kd一样，K1，K2随滑翔飞行器的飞行高度和速度变化而变化。

加入协调控制支路后偏航通道的舵摆角为:

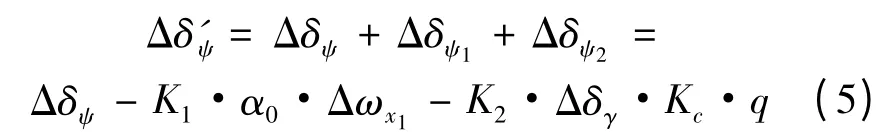
根据交连耦合最小的原则进行参数K1，K2的选择，可得到在此状态下K1，K2分别为K1= 27，K2= 4.5。最后可得到如式(3)的新的三通道耦合矩阵G″为

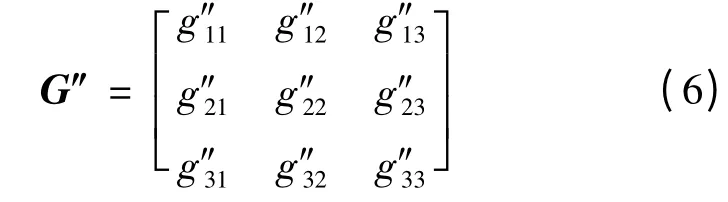
按照频率可画出矩阵G″ 在一定频率范围的对角优势度图形，如图8 所示。

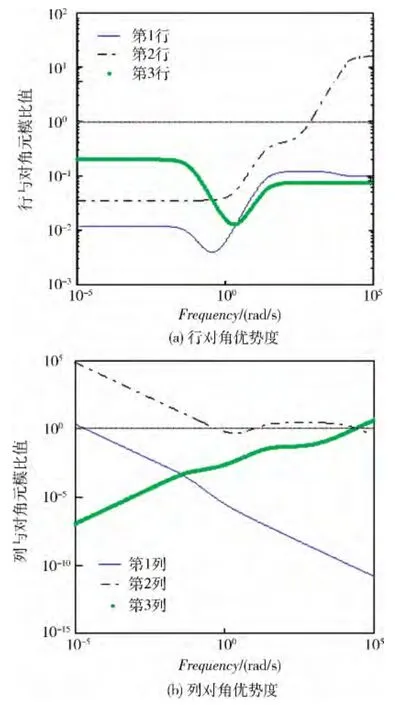
图8 加入协调支路控制的对角优势度图

对比协调控制前后传递函数矩阵的行列对角优势度图，可以看出，经过补偿，加入协调控制支路，滑翔飞行器三通道之间的交连耦合问题得到了较好解决，加入协调支路后，系统的传递函数矩阵在0(rad/s)＜ω ＜900(rad/s)的频率范围内是对角优势的，可以认为系统在工作频率内是解耦的。

4 滑翔飞行器三自由度非线性仿真

为了检验加入协调支路的控制效果，需要进行滑翔飞行器三自由度非线性仿真。假设:滑翔飞行器的飞行高度和速度不变;动压不变;初始状态为配平状态Ma0= 20，h0= 50km，α0= 8.5°，β0= 0°，δφ0= 8.7764615°，δφ0= δγ0= 0° 。

仿真得到的结果如图9 ～11 所示。

图9 攻角随时间变化曲线

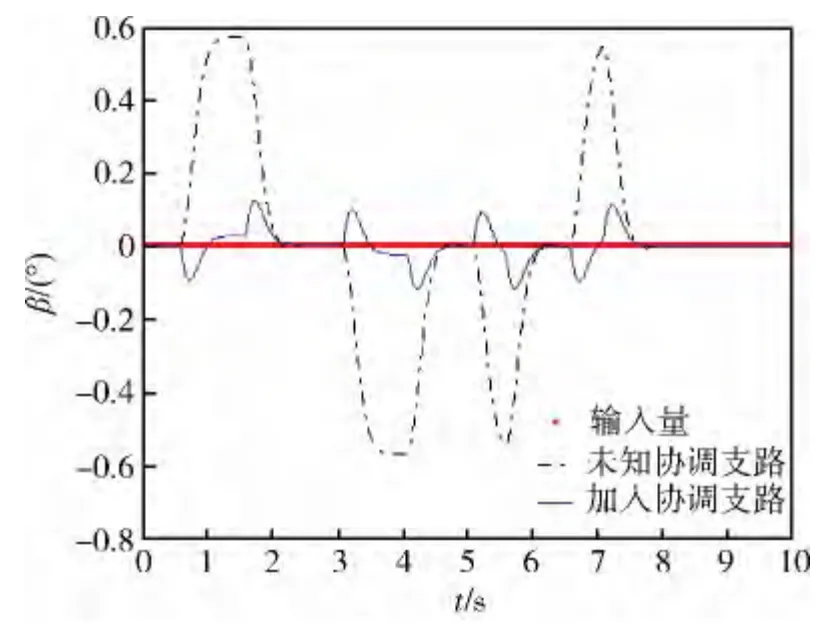
图10 侧滑角随时间变化曲线

仿真中俯仰通道和偏航通道的输入α，β 固定不变，滚转通道的输入γv为梯形波组成。由图9 和11看出，加入协调支路前后控制系统俯仰通道和滚转通道变化不大，效果差不多，这说明滑翔飞行器的俯仰和滚转通道受到其他通道的干扰比较小。从图10 可以看出，加入协调控制支路后侧滑角明显减小了，达到了严格控制侧滑角的目的，这说明协调控制是有效的，参数的选择也是合理的。

图11 速度倾斜角随时间变化曲线

5 结论

对高超声速滑翔飞行器采用BTT 控制技术进行三通道独立设计，然后加入协调控制支路进行补偿解耦，其中三通道独立设计采用自适应PID 方法，控制器参数随飞行高度和速度的变化而变化。设计了变增益的协调控制支路来补偿系统的交连耦合。通过三自由度非线性仿真对控制方案和控制参数进行检验，仿真结果表明，设计的控制方案是正确的，控制参数的选择是合理的，达到了严格控制侧滑角的目的。

［1］崔平远，全胜，吴雁林. BTT 导弹机动飞行非线性解耦控制［J］. 飞行力学，2000，18(2):39 －41. (Cui Ping yuan，Quan Sheng，Wu Yan lin. Nonlinear decoupling control for bank-to-turn missile ［J］. Flight Dynamics，2000，18(2):39 －41. )

［2］赵霞. 防空导弹BTT 解耦算法［J］. 四川兵工学报，2013，34(8):37 － 40. (Zhao Xia. Research on BTT control decoupling algorithm for the air-defense missile［J］. Journal of Sichuan Ordnance，2013，34(8):37 －40.)

［3］Mooij E. Direct Model Reference Adaptive Control of a Winged Re-entry Vehicle［C］. AlAA 9thInternation Space Planes And Hypersonic Systems And Technologies Conference，November 1-4，1999，Norfork，VA.

［4］高黛陵.多变量频率域控制理论［M］. 北京:清华大学出版社，1998.