基于ADAMS的电力液压盘式制动器仿真研究
姜朝俊,田树涛,孔祥虎
(1.山东省天安矿业有限公司,山东 济宁 272000;2.山东科大机电科技股份有限公司,山东 济宁 272000)
基于ADAMS的电力液压盘式制动器仿真研究
姜朝俊1,田树涛2,孔祥虎2
(1.山东省天安矿业有限公司,山东 济宁 272000;2.山东科大机电科技股份有限公司,山东 济宁 272000)
以电力液压盘式制动器为研究对象,利用ADAMS软件进行建模仿真,优化分析获得制动器所需要的制动力矩和间隙。仿真数据与试验数据对比表明:ADAMS软件的分析结果和试验数据基本吻合,为制动器的设计和计算提供了可靠的方法和依据,节省了研发费用并缩短了开发周期。
ADAMS; 电力液压盘式制动器; 动力学分析; 仿真
0 引言
电力液压盘式制动器是煤矿、冶金、港口码头等行业常用的一种常闭结构制动装置,其主要由电力液压推动器、制动弹簧、制动闸瓦、一套或者多套连杆机构等组成。杠杆比是电力液压盘式制动器非常重要的结构参数,它是施加在制动盘上的正压力与电力液压制动器推力的比值,一般都是手动计算系统杠杆比,然后做样机进行试验,该方法计算复杂,制样周期长,开发费用高。本文提出了一种应用动力学分析软件ADAMS对制动器杠杆比进行分析的方法,并对制动器杠杆比进行优化,比较理论分析和试验的数据用以检验理论分析的正确性。
1 电力液压盘式制动器分析模型
1.1 制动器参数
KDUB500-2060电力液压盘式制动器参数见表1,制动器外形及结构简图如图1所示,并以铰点1与铰点2的连线为X轴,铰点1与铰点2的中点为Y轴建立坐标系。

表1 KDUB500-2060电力液压盘式制动器参数
1.2 构建虚拟样机模型
在建模分析过程当中,不需要将所有的动作以及零部件都考虑进去,而应根据具体的仿真目的和需要合理地忽略删减不必要的部分,以达到仿真目的的同时尽可能地简化模型。本模型的基本假设如下:①忽略所有铰接点的摩擦力;②忽略所有零部件的重力作用(系统重量轻,对系统分析基本没有影响);③各零部件为刚体,即不会产生任何变形。本文采用ADAMS本身自带的构建模型功能构建制动器模型,对模型的各零部件进行物理信息的定义,包括构件名称的修改、材料属性的修改等。整个模型中共有7个刚体、一个弹簧、9个旋转副、2个平行副和1个施加力(弹簧工作载荷)。
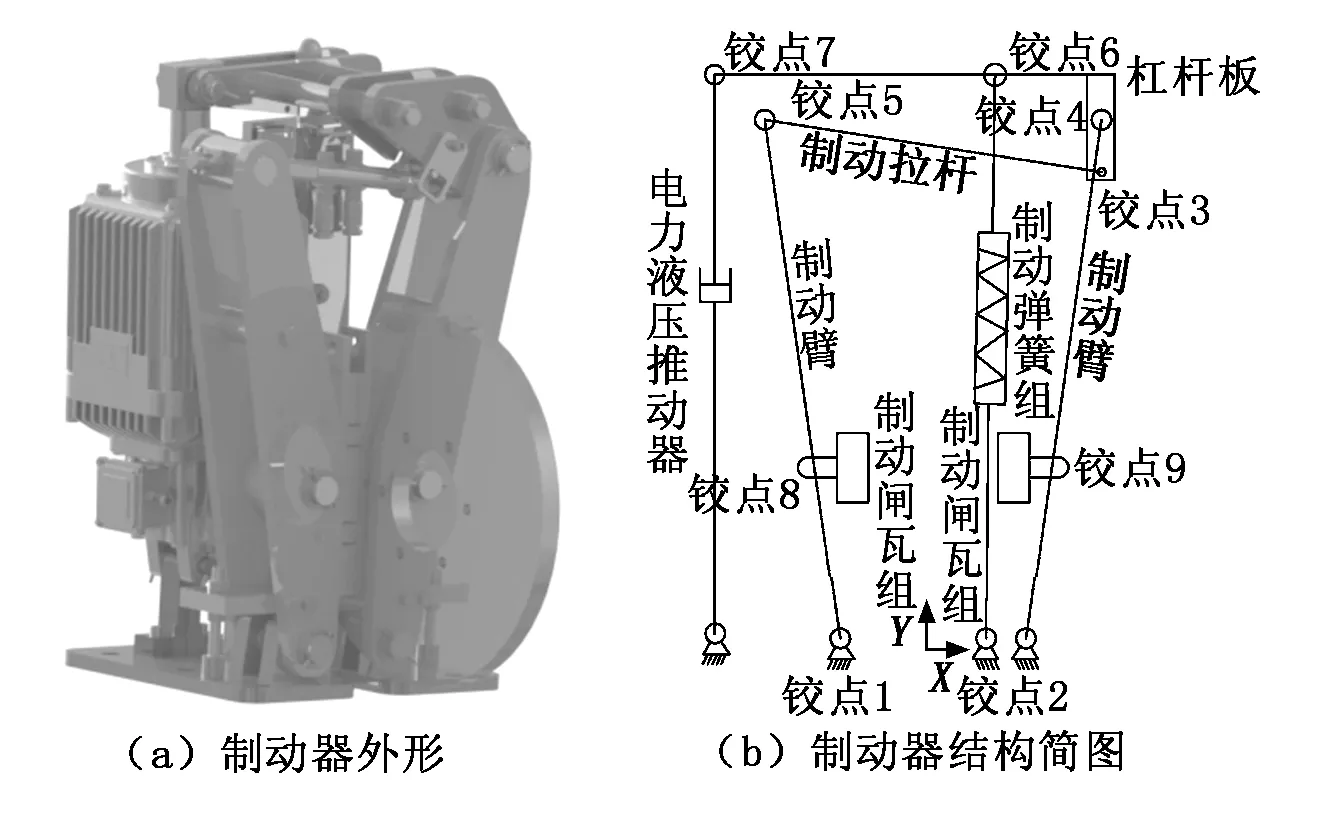
图1 制动器外形及结构简图
1.3 分析工况
制动器分为开闸和闭闸工况,开闸是由推动器、制动弹簧和平面铰点组组成杠杆系,简单分析推动器和制动弹簧的杠杆比,即可求得推动器克服的最大弹簧力。闭闸工况是系统在制动弹簧力的作用下,将弹簧力增比后传递到制动闸瓦上,通过和制动盘的配合产生制动力,进而对系统进行制动,根据弹簧最小工作载荷和最大工作载荷以及工作行程即可设计制动弹簧,这也是制动器的核心技术。与闭闸工况相比,开闸工况较简单,所以本文主要分析闭闸工况。
1.4 计算制动力矩
根据ADAMS软件特性,分析出制动器闸瓦的正压力,再根据公式M=NFRμ(其中,M为制动力矩,N为摩擦副数量,F为正压力,R为制动理论半径,μ为摩擦因数)计算得出制动力矩。
2 制动器杠杆比优化和仿真
在制动器分析中,最重要的就是分析制动器系统的杠杆比,杠杆比越大,产生的正压力也越大,相应地制动力矩也越大,但开闸间隙会变小,所以要在开闸间隙和制动力矩之间寻求最优组合。开闸间隙一般为1 mm~2 mm,优化制动器杠杆比,实现最大制动力矩。2.1 制动器制动力矩分析
在弹簧处施加弹簧最小工作载荷850 N,在闸瓦处设置正压力测力弹簧,仿真设置如下:结束时间为4 s,步骤为200。将数值代入M=NFRμ计算得M=2 060 N·m。
2.2 优化设计变量
由于制动器铰点较多,一般我们会通过ADAMS软件的优化设计变量功能将每个铰点X、Y(坐标参考图1)方向的数值参数化,找出对系统正压力敏感的几个铰点坐标,单独计算每个设计变量对正压力的敏感度。计算得到的制动器铰点设计变量对正压力的敏感度如表2所示。
由表2可以看出:设计变量DV_6、DV_11、DV_16的敏感度最高,也就是说铰点3_Y、铰点6_X、铰点8_Y的位置变化对制动器系统的正压力影响最大。
2.3 优化设计杠杆比
由表2分析得知:铰点3_Y方向坐标、铰点6_X方向坐标、铰点8_Y方向坐标对制动力矩影响最大,设它们的数值分别用a、c、b表示。在ADAMS中,将铰点坐标的数值浮动范围控制在±10%,分析每个铰
点坐标的数值与制动力矩和开闸间隙之间的关系。分析结果如图2、图3和图4所示。
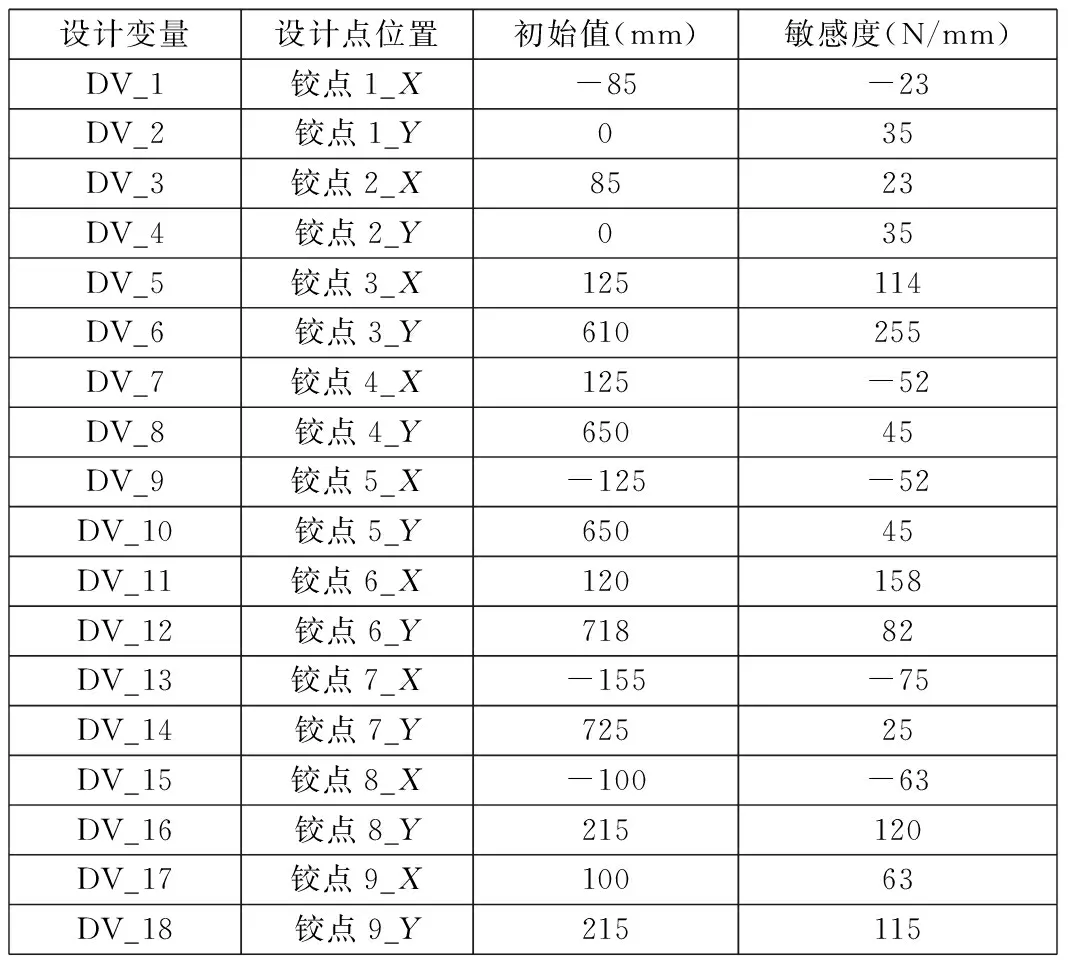
表2 设计变量对正压力的敏感度
在满足开闸间隙1 mm~2 mm的条件下,通过模拟优化,得到最大正压力时a、b、c的数值,如表3所示。
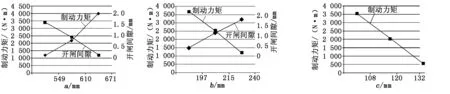
图2a与制动力矩和开闸间隙的关系 图3b与制动力矩和开闸间隙的关系 图4c与制动力矩的关系(c与开闸间隙无关)
3 制动器仿真结果与样机试验结果对比
根据仿真模型设计生产了一台物理样机,型号为KDUB500-2060,开闸间隙为1.5 mm。物理样机试验结果与仿真分析结果对比如表4所示。
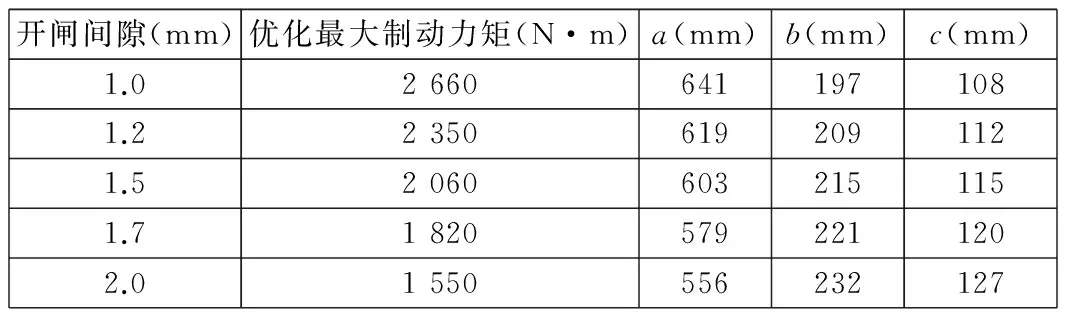
表3 优化数值表
由表4可知,两者偏差较小,在10%之内,存在偏差的原因主要是:未考虑弹簧的富余系数,摩擦因数浮动空间在0.35~0.45之间,且在试验当中需考虑系统的摩擦阻力,总体来说,仿真结果与试验结果基本一致。4 结束语
综上所述,ADAMS软件能够很好地仿真优化设计电力液压盘式制动器,与试验结果比较接近,能够满足工程精度和使用要求。

表4 物理样机试验结果与仿真分析结果对比
[1] 高广娣.典型机械机构ADAMS仿真应用[M].北京:电子工业出版社,2013.
[2] 范建成,熊光明.虚拟样机软件MSC.ADAMS应用与提高[M].北京:机械工业出版社,2006.
[3] 孙恒,陈作模.机械原理[M].北京:高等教育出版社,2006.
[4] 梅经武.起重机用盘式制动器[J].起重运输机械,1992(11):25-26.
[5] 王新伟,郭冬梅.盘式制动器在带式输送机上的应用[J].起重运输机械,2005(11):62-63.
Simulation of Electro-hydraulic Disc Brake Based on ADAMS
JIANG Chao-jun1, TIAN Shu-tao2, KONG Xiang-hu2
(1.Shandong Tian’an Mining Co.,Ltd., Jining 272000,China; 2.Shandong Keda M&E Technology Co., Ltd., Jining 272000,China)
Taking an electro-hydraulic disc brake as research object, this paper carried out the simulation analysis on electro-hydraulic disc brake, getting braking moment and clearance. Experimental data show the analytical results of ADAMS agree with that of experimental data. It provides a reliable method and basis for the design of brakes.
ADAMS; electro-hydraulic disc brakes; dynamic analysis; simulation
1672- 6413(2015)06- 0080- 02
2015- 09- 14;
2015- 11- 02
姜朝俊(1968-),男,山东阳谷人,工程师,本科,现从事煤矿机电设计工作。
TP391.7
A

