三分量磁通门传感器的三轴正交校正与测量

王一,宗发保,赵瑜,程德福*

吉林大学仪器科学与电气工程学院,吉林长春130061

三分量磁通门传感器的三轴正交校正与测量

王一,宗发保,赵瑜,程德福*

吉林大学仪器科学与电气工程学院,吉林长春130061

受机械加工与安装水平的限制，磁通门传感器的三个分量相互之间无法保证绝对正交，由此会带来三分量磁测数据误差。本文通过建立一种三轴正交角度与磁总场误差关系模型，并对该模型进行正演模拟、反演分析及建立一种修正算法，达到推算三个分量不正交角度并修正的目的。实验表明，采用该方法对实际三分量磁通门传感器进行不正交度的测试与修正后，能够使其在测量总场时的误差减小到±10 nT，减小了测量时所带来的误差。

三分量磁通门传感器;正交度校正;非线性最小二乘最优化

磁通门磁力仪在二战时期就被装载于低空飞行器用于潜艇目标的探测，其后又被广泛搭载于卫星和航天器上用于空间磁场的测量。单分量磁通门探头只能测得某一方向的磁场分量，而三分量磁通门探头可以同时测得空间某点处的所有磁场分量，经过计算也可以获得总场、矢量及各个角度参数。三分量探头可由三个参数一致的单分量探头正交组装而成，可应用于地磁测量、舰船磁测、导航等领域[1-3]。

受机械加工与安装水平的限制，磁通门探头的三个分量相互之间无法保证绝对正交，由此会带来三分量磁测数据误差，由分量计算得到的总场也同样存在误差。文献[4]采用共轭梯度法校正了对三轴磁传感器正交性误差进行了校正。文献[5]以三轴磁强计实际输出的求模计算结果与实际磁场矢量模值间的误差为指标，进行了理论计算，求解出变换系数，对三轴磁传感器进行了校正。文献[6]应用了基于扩展卡尔曼滤波和无迹卡尔曼滤波的两种算法对三轴磁传感器进行校正，并将校正结果进行了比较。文献[7]提出一种基于函数链接型神经网络(FLANN)的三轴磁强计误差修正方法，过构造相应的FLANN网络结构实现对模型参数矩阵的辨识，对模型参数矩阵进行辨识和校正。文献[8]中提出了一种循环优化算法,将优化算法引入全部固有误差的校正,采用循环计算求得误差校正参数。

本文通过建立一种三轴不正交角度与磁总场误差关系模型，并对该模型进行正演模拟，研究给定范围内的不正交角度对磁总场测量的影响，并基于非线性最小二乘最优化方法，研究从给定磁场数据推算不正交角度并修正的方法。最后通过实验测试实际探头的不正角度和修正算法，验证了修正方法的正确性，达到了预期的效果。

1　模型建立与分析

1.1三轴不正交体系的坐标变换

暂不考虑灵敏度和零点偏移，仅考虑三轴不正交角度对磁场测量的影响。建立如图1所示的不正交坐标系，O’X’Y’Z’为探头坐标系，OXYZ为理想正交坐标系，令三分量灵敏度修正系数均为1，零点偏移修正系数均为0，三轴的不正交角度分别为α、β、90-γ。

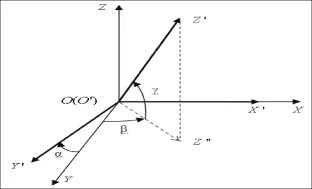
图1　不正交坐标系Fig.1 Non-orthogonal coordinate system

三个单分量探头测到的磁感应强度Bx’，By’，Bz’与直角坐标系中的磁感应强度Bx，By，Bz的关系为：

其中，变换矩阵T为：

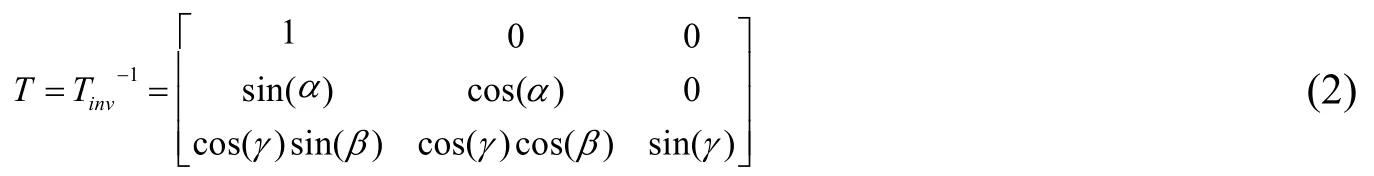
1.2总场误差的正演模拟

正交坐标系中的总场B、探头坐标系中的总场为B'分别为,

总场误差△B为:

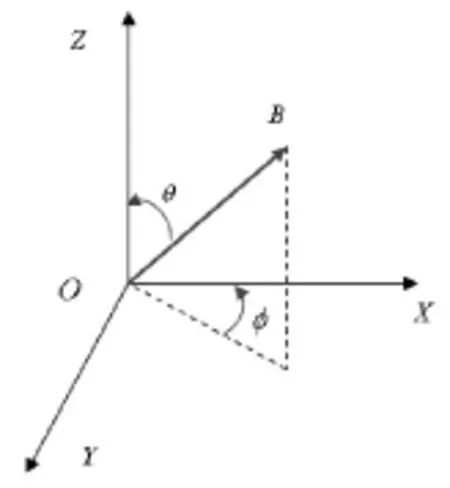
图2　总场B在坐标下的分解示意Fig.2 Decomposition diagram of the geomagnetic total field B at the coordinate system

在图2坐标系OXYZ中，将外界磁场B分解后有:

则探头坐标系下的磁场与正交坐标系下的磁场表示为:

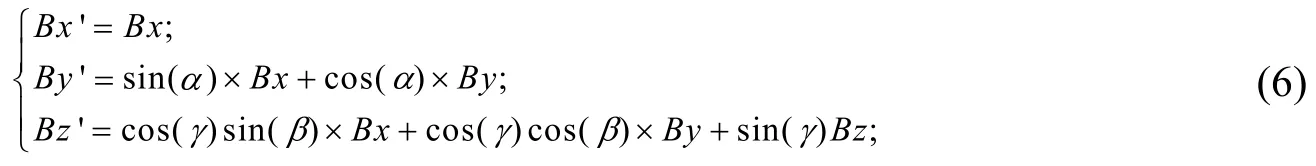
将Bx,By,Bz带入式（6）有:

由式（4）可知，总场误差可表示为，

其中，B为外界磁场总场大小:

α、β、90-γ°为三轴不正交角度，α、β趋近于0°，γ趋近于90°；

θ、φ为外界磁场在正交坐标系下的分解角度，θ的取值范围为0～360°，φ的取值范围为-90°～90°；为求总场误差的最大值，我们选择求如式（9）所示目标函数的最小值。

当给定α、β、γ时，求Hobj的最小值min(Hobj)是一个有约束非线性规划问题，约束条件为:

1.3数值计算分析

非线性最小二乘法以误差的平方和最小为准则来估计非线性静态模型参数的一种参数估计方法[9-11]。设非线性系统的模型为y=f(x，θ)，常用于传感器参数设定[12,13]。针对式（9）进行有约束非线性规划问题求解，其中几种典型不正交角度[α°，β°，90-γ°]的正演模拟结果如表1所示，

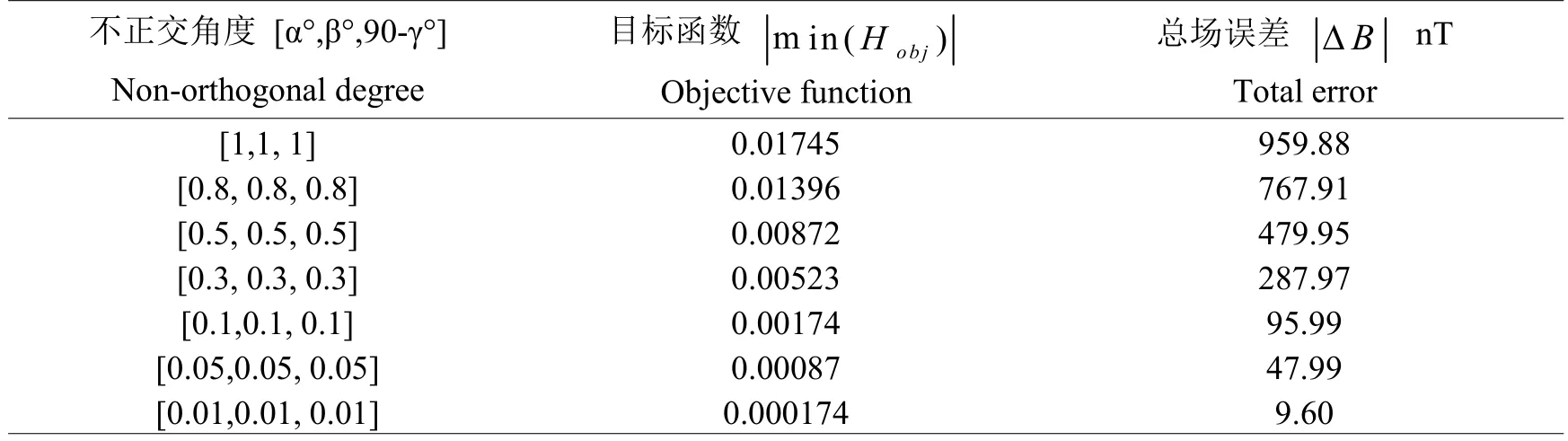
表1　几种典型不正交角度的正演模拟结果Table 1 Several forward modeling simulation results of typical non-orthogonal angle

为了验证表1的正演模拟结果，我们选取不正交角度[0.1，0.1，0.1]进行做仿真，其在全空间各个方向的总场误差分布如图3所示，其最大值约为95 nT，与正演的结果一致。

为了清楚的表示整个球面的误差分布，以球面坐标的θ、φ为自变量将球面投影到如图4的矩形平面后，可以直观的看到总场误差主要分布于四个区域，红色代表正，蓝色代表负。

2　测量与修正算法

三分量探头的三轴不正交角度通常是未知的，需要我们通过其给总场测量带来的误差反演求出。该反演方法为：在给定的角度范围内，寻找参数α、β、γ使得如式（4）取得最小值，其中，Bx’，By’，Bz’为探头观测到的磁场，B为外界磁场大小。

在一个磁场均匀恒定的空间，转动探头，依次记录下各个等概率的各个方向上的分量值Bi’=[Bxi’，Byi’，Bzi’]T（i从0～N，数据点数N＞＞3）。

图3　总场误差分布Fig.3 Total field error distribution

图4　以θ、φ投影后的球面Fig.4 The sphere projection of θ,φ

寻找参数α、β、γ使得目标函数Hobj取得最小值，α、β、γ的边界条件有限，边界上限为最大误差角度的估计值，常由传感器厂家给出。

选取的目标函数为：

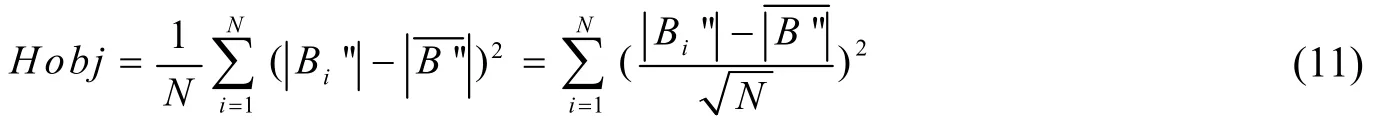
其中，Bi”为正交坐标系中的磁场Bi”=Tinv×Bi’，Tinv为不正交修正矩阵，为││总场，为所有磁总场的平均值。

反演模型可表示为:

为了验证该反演方法，令外界磁场为55000 nT，我们先从不正交角度[0.07°，0.04°，0.1°]正演的结果中随机抽取一批数据用于测试，抽取到的磁测数据如表2所示。

表2　正演后的数据点Table 2 The data points of forward modeling

下边界条件为[-0.5°,-0.5°,0.5°]，上边界条件为[0.5°,0.5°,0.5°]，求解初值[0°,0°,0°]，求解精度为1×10-6。采用非线性最小二乘法求解，求解的迭代过程如表3所示。

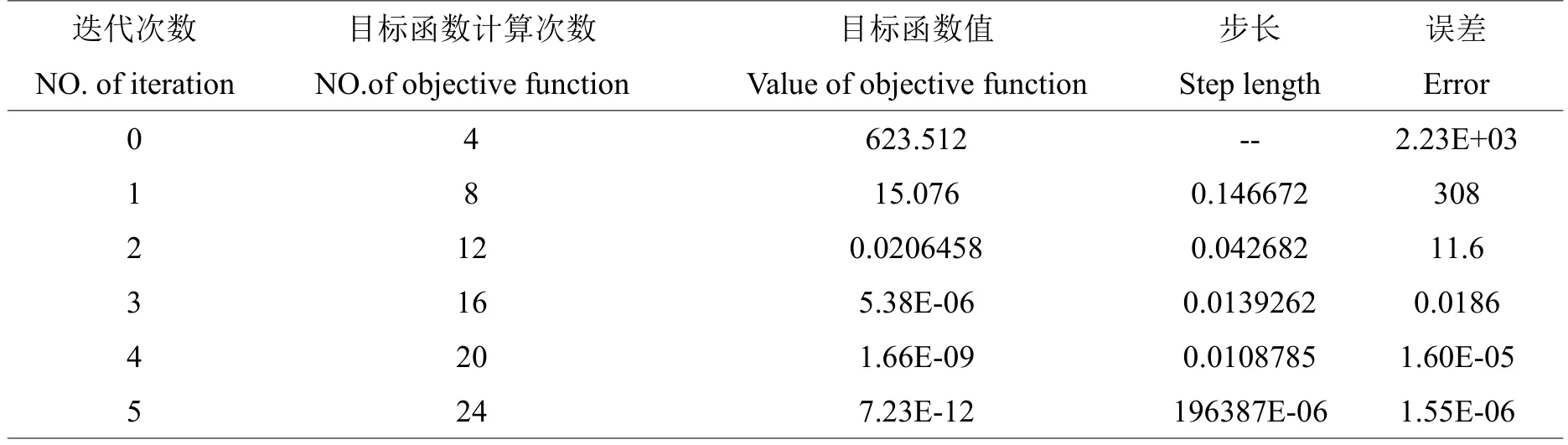
表3　迭代过程Table 3 The iterative process

求解结果为[0.07°，0.04°，0.1°]，与正演的参数一致。

图5是不正交修正前后的总场对比曲线，波动较大的曲线为不正交修正前的磁总场，波动很小的曲线为不正交修正后的磁总场。

综上所述，反演结果与正演的参数一致，修正后能消除由不正交带来的磁总场误差，该反演方法是可行的，且消耗时间短。当采用实际数据做反演时，三分量灵敏度、零点偏移、环境噪声及仪器噪声均会对磁场测量带来影响，进而影响反演的精度。我们将对同一探头进行多次重复实验并对多次实验的反演结果进行比较，最终确定探头实际的三轴不正交角度及其误差范围。

3　实验验证

采用上述方法，在野外某处磁场干扰较少的地方，缓慢地转动探头，尽可能让其均匀地指向空间球面的各个方向，记录下所有的磁场数据用于反演。反演修正结果如图6所示。

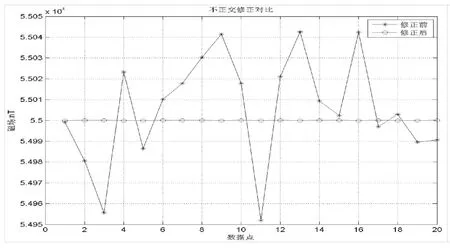
图5　不正交修正前后对比Fig.5 The contrast before and after non-orthogonal correction

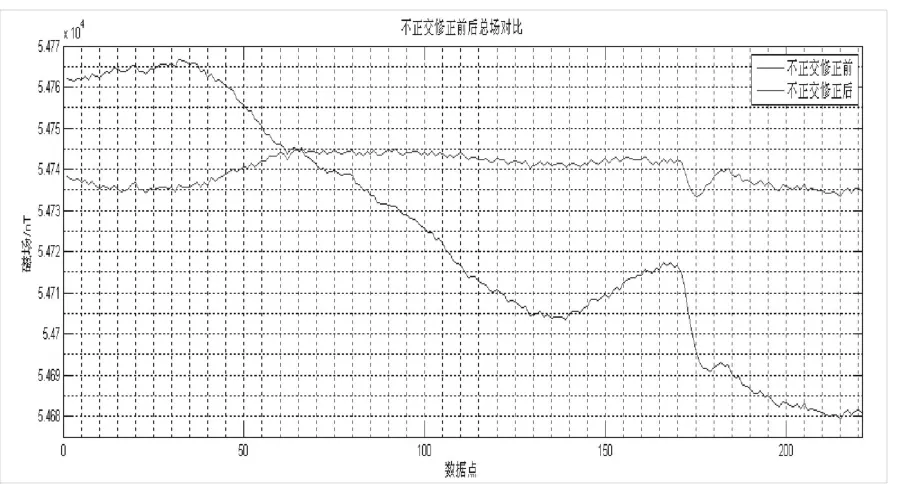
图6　三分量磁传感器进行不正交度修正后的总场对比Fig.6 Contrast of three components magnetic sensor after non-orthogonal correction

在随后的多次实验中，反演结果与均值的误差小于0.004°，误差角度α=0.064°、90o-γ=0.103°，修正矩阵Tinv为:

由正演的结论可知，该0.004°的角度误差在全空间下带来的总场测量误差不会超过3.8 nT。

表4　同一探头多次实验的反演结果Table 4 The inversion results of repeated experiments in the same sensor

4　结语

对三分量磁通门传感器的正交角度校正,是进行三分量磁场测量工作的必要基础。本文首先建立一种三轴不正交角度与磁总场误差关系模型，并对该模型进行正演模拟用于确定给定范围内的不正交角度对磁总场测量的影响。其次，所进行的反演分析以及修正算法是基于非线性最小二乘最优化，研究从给定磁场数据推算不正交角度并修正的方法。最后，在对实际探头的实际实验中，验证了测试与修正方法的正确性。本文研究的不正交角度校正技术对其它种类三分量测量具有参考价值。

[1]闫辉,肖昌汉.一种海洋环境地磁场三分量的测量方法[J].海军工程大学学报,2005,17(6):80-84

[2]蔡体菁,刘莹,宋军,等.嵌入式GPS/MIMU/磁罗盘组合导航系统[J].2010,31(12):2695-2699

[3]谢川.一种基于磁强计和倾角传感器的钻井测斜仪[J].仪器仪表学报,2010,31(10):2357-2362

[4]胡海滨,林春生,龚沈光.基于共轭次梯度法的非理想正交三轴磁传感器的修正[J].数据采集与处理,2003,18(1):88-91

[5]林春生,向前,龚沈光.三轴磁强计正交误差分析与校正[J].探测与控制学报,2005,27(2):9-12

[6]CRASSIDIS J L,KOK-LAM L,RICHARD R H.Real-time attitude-independent three-axis magnetometer calib ration[J].Journal of Guidance,Control and Dynamics,2005,28(1):115-120

[7]吴德会,黄松岭,赵伟.基于FLANN的三轴磁强计误差校正研究[J].仪器仪表学报,2009,30(3):449-453

[8]周超烨,金际航,李宏武,等.三分量磁通门传感器校正的循环优化算法[J].海洋测绘,2010,30(4):63-67

[9]肖爱玲.非线性最小二乘法的算法(英文)[J].数学理论与应用,2004(2):86-90

[10]董志荣.纯方位系统TMA非线性最小二乘法——工程数学模型与算法[J].情报指挥控制系统与仿真技术,2005(4):4-8

[11]邢书珍,邢天奇.非线性最小二乘拟合的计算方法[J].中国铁道科学,1995(3):64-71

[12]孙德辉.传感器线性精度计算方法的选用问题[J].传感器技术,1984(3):31-38

[13]雷雨,冯新喜,朱灿彬,等.基于测距最小二乘的方位融合多传感器定位算法[J].电光与控制,2012(1):12-17

Calibration and Measurement on the Orthogonal Three-axes of Three-components Magnetic Flux-gate Sensor

WANG Yi,ZONG Fa-bao,ZHAO Yu,CHENG De-fu*
College of Instrumentation and Electrical Engineering,Jilin University,Changchun 130026,China

Magnetic flux-gate sensor is limited by the installation and process,its three-components can not be absolute orthogonal between each other,so as to bring with measurement errors for data.In order to solve this problem,a new relational model of the three-axis orthogonal angle and magnetic field error is established,simulated,analyzed inversely and to set up a correction algorithm at end.The experimental results showed that the measurement error of magnetic field is reduced to±10 nT after using this method to test and calibrate the non-orthogonal degrees of the three-components magnetic flux-gate sensor,and the measurement error has been significantly reduced.

Three-components magnetic flux-gate sensor;orthogonal calibration;non-linear the least square optimization

P631文献识别码:A

1000-2324(2015)02-0232-06

2013-06-08

2013-07-11

国家“863”重大项目(2013AA063901);国家重大科研装备研制项目(ZDYZ2012-1);吉林大学研究生创新研究计划(20121071)

王一(1982-),男,博士研究生.研究方向:航磁三分量矢量勘查技术研究.E-mail:wang_yi321@sina.com

Author for correspondence.E-mail:chengdefu@jlu.edu.cn