基于0.18 μm的无电阻无运放低功耗带隙基准源设计

李燕霞，龚 敏，高 博

（四川大学物理科学与技术学院，成都 610065）

1 引言

在集成电路设计中，基准源是模拟和数模混合电路中不可缺少的重要组成部分，它对高新模拟电子技术的应用与发展具有重要的作用。在许多集成电路中，如数/模转换线性稳压器和开关稳压器等，都需要稳定的电压基准；并且随着SOC片上系统的发展，超大规模集成电路对于带隙基准源的精度和功耗逐渐有着更高的要求，并且要求其能与CMOS工艺相兼容。基准电压源有基于正向的基准电压、基于齐纳二极管反向击穿特性的基准电压以及带隙基准电压。其中带隙基准电压由于其低温度系数和高的电源抑制比而得到广泛应用[1]。

2 传统带隙基准源的基本原理[1]

传统的带隙基准源核心结构是由BJT和电阻构成，为了钳制电压加入了运算放大器；其工作原理是通过正负温度系数的叠加来得到与温度无关的基准电压的输出，如图1所示。

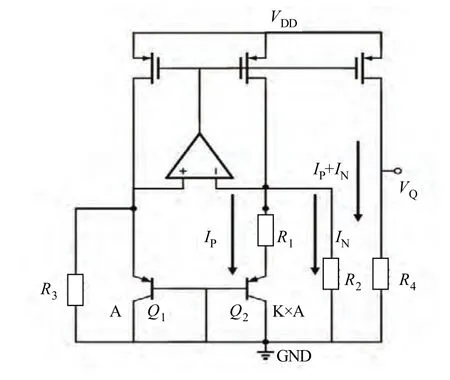
图1 传统的带隙基准源结构

对于一个工作在放大区的BJT来说，其基射极电压具有负的温度系数，当两个BJT的电流密度相同时，其基极-发射极电压的差值为：

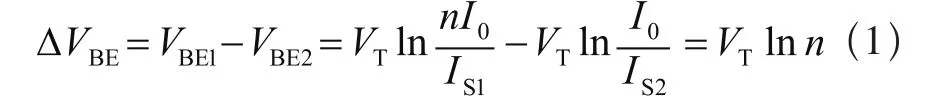
因此R1上的电压为VR1=VTlnn，其中VT=kT/q，n是晶体管Q1和Q2的面积之比，由此可见其基射极电压差具有正的温度系数，采用求和的方式将正负温度系数电压进行叠加就可以在某温度上得到基准电压：

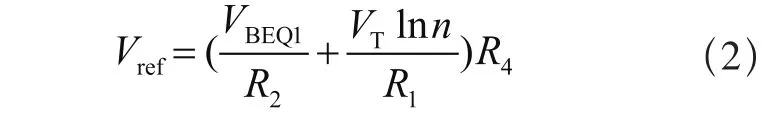
精确调节电阻的阻值便可以得到与温度无关的电压，但是由于VBE具有高阶的温度系数，这样的传统结构由于只能实现一阶温度系数的补偿，因此其温漂系数比较高。此外为了钳制电位，电路中需要设计高性能的运算放大器，这不仅增加了设计工作量，也大大提高了其复杂度。再加上在CMOS工艺中，要实现电阻的精确匹配具有很高的难度，综合上面几个因素，传统的带隙基准源电路所具备的实用性很低[2]。

3 无电阻无运放的带隙基准源结构

如上所述，电路中运放的设计和电阻的精确匹配会给设计增加难度，因此本文采用如图2所示的电路结构。在该电路结构中，Q1的结电压由MN1和MN2的栅源电压钳制，流经Q1的发射极电极电流也由MP1和MP2形成的电流镜结构决定。因此，适当地设置电流比例K和MN1管和MN2管的宽长比，就能够得到一个非零的电压偏置点来对BJT和MOSFET进行偏置。假设MN1和MN2具有相同的宽长比，那么VE就被平均分成VGS1和VGS2两部分。由于BJT的VBE具有负的温度系数，因此将此电压和一个具有正温度系数的电压叠加即可得到与温度无关的基准电压。在该电路结构中，产生正温度系数的电压来自于由M2~M7构成的self-cascode结构[4]。

图2 无电阻无运放的带隙基准源

4 电路原理阐述

4.1 CTAT电压的产生

对于一个双极型器件，集电极电流由式（3）给出：

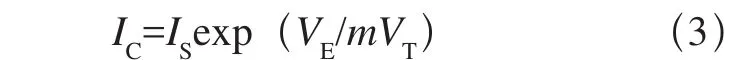
其中IS是pn结的饱和电流，VT=kT/q是BJT的热电压；当图2中所有的MOSFET都工作在亚阈值区域时，根据ACM MOSFET模型，漏电流的表达式如式（4）。

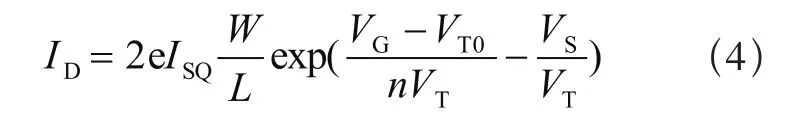
其中，e为常数，ISQ为电流密度，VT0是忽略体效应时的阈值电压，VG和VS是栅极和源极相对于衬底的电压值。在MN1和MN2具有相同宽长比的前提下：

再根据MP1和MP2组成的电流镜结构可得：

因此VE可以写成式（8）：

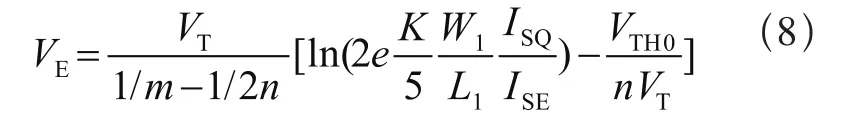
4.2 PTAT电压的产生

PTAT电压的产生来自于传统的self-cascode 结构[12]，由图3可知，在self-cascode结构中：

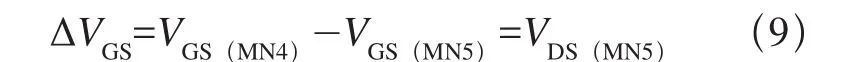
由式（4）和式（9）可得：

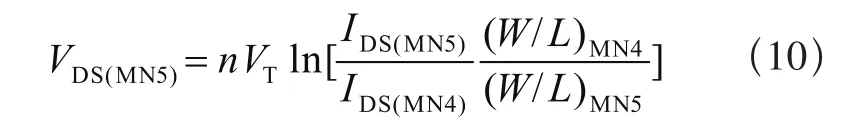
由式（10）可知，在本文的电路结构中：

根据电流镜结构：IDS（MN2）=5I，IDS（MN5）=4I，IDS（MN7）=3I，结合式（10）和式（11）可得式（12）：

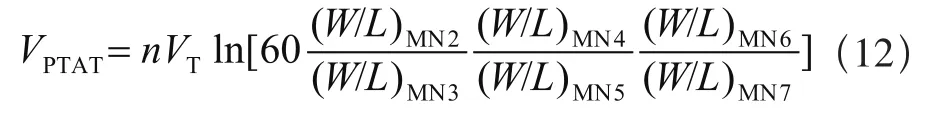
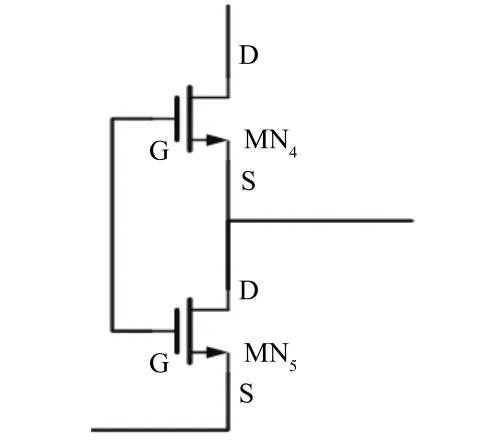
图3 self-cascode结构

4.3 基准电压

根据式（5）和式（12）可知基准电压的表达式为：

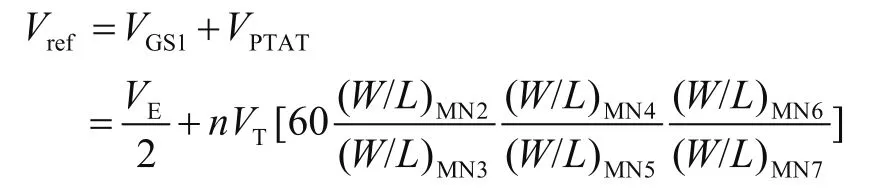
4.4 补偿电路[8]

由于VE具有高阶的温度系数，因此采用图2 Q2和Q3部分构造指数型补偿电路。其中流经Q3的集电极电流是一个与温度成高阶温度关系的量，把这一电流引入带隙基准源的输出端可以对带隙基准源进行高阶的温度补偿。该补偿电路的两个三极管的集电极均接电源电压，这样与标准的CMOS工艺就可以完全兼容。

5 仿真与分析

采用SMIC 0.18 μm工艺库，在1.2 V的电压下利用Spectre工具对整体电路进行仿真，得到图4和图5的温度曲线。

由图4可知，初步仿真的温度曲线为开口向下的抛物线，其温漂系数为24.38×10-6℃-1。在高温区电压变化比较大，采用指数型曲率补偿电路之后，仿真结果如图（5）所示：在高温区域输出电压的变化明显变小，温漂系数也由补偿之前的24.38×10-6℃-1降低为8.4×10-6℃-1，输出的基准电压为569 mV，功耗仅为742 nW。与其他文献相比，本文设计的与CMOS工艺兼容的带隙基准源的温漂系数，远远小于国际上已有的和CMOS兼容的电压基准电路，如表1所示。图6是该电路的版图。

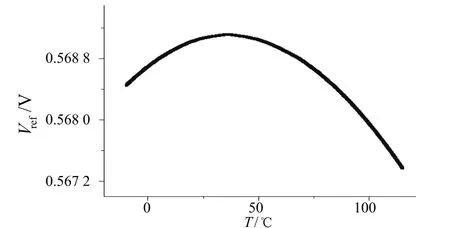
图4 补偿前温度曲线

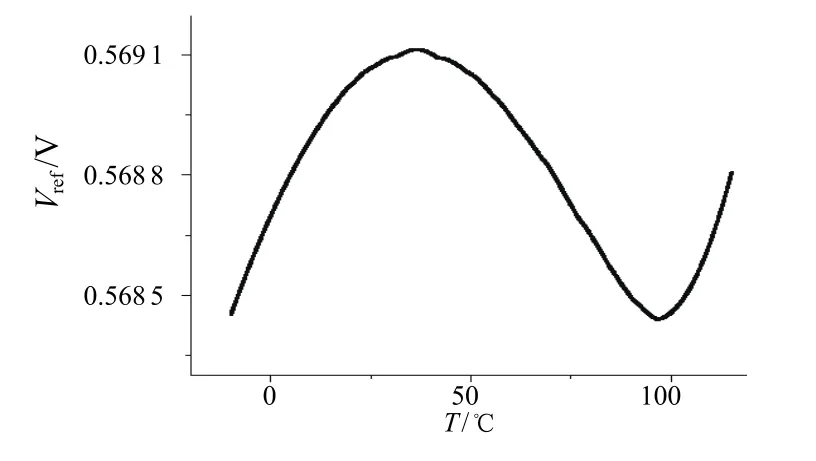
图5 补偿后温度曲线

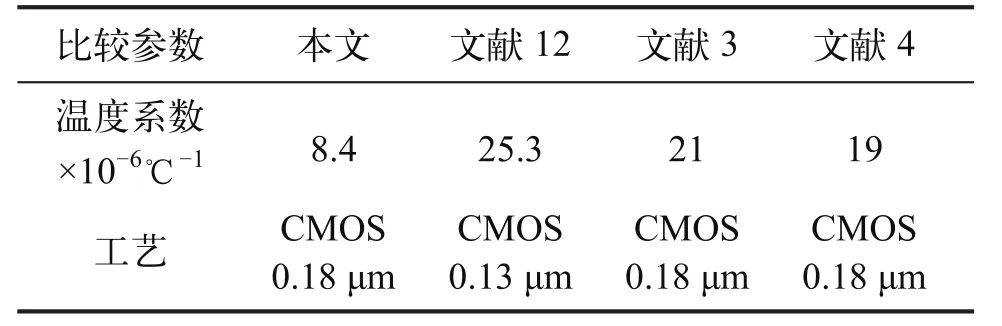
表1 温度系数对比

图6 电路版图

6 总结

本文采用SMIC 0.18 μm工艺库设计了一种带有高阶曲率补偿的带隙基准源电路结构，该电路结构具有无电阻无运放的特点，相对于传统的带隙基准源电路来说本文设计电路结构简单，在工艺上能够很好地与CMOS工艺兼容，并且具有较低的温漂系数和极低的功耗。

[1] 毕查德拉扎维. 模拟CMOS集成电路设计[M]. 2003.310-320.

[2] 陆云，李严，董子刚，张元亭. 基于MOS技术的基准源电路研究进展[J]. 2014, 04.

[3] Lee, E K F. Low voltage CMOS bandgap references with temperature compensated reference current output[J]. Circuits and Systems（ISCAS）, Proceedings of 2010 IEEE International Symposium on, 2010. 1643-1646.

[4] Adl, A-H El-Sankary, K El-Masry, E. Bandgap reference with curvature corrected compensation using subthreshold MOSFETs [J]. Circuits and Systems, ISCAS 2009, IEEE International Symposium on, 2009. 812-815.

[5] Dalton Colombo, Felipe Werle, Gilson Wirth, Sergio Bampi. A CMOS 25.3 ×10-6℃-1Bandgap Voltage Reference using Self-Cascode Composite Transistor [J]. IEEE . 2012.

[6] 唐宁，李佐，李琦. 一种改进的非线性匹配高阶补偿基准源的设计[J]. 2013.

[7] Oscar E Mattia, Hamilton Klimach. 0.9 V, 5 nW, 9×10-6℃-1Resistorless Sub-Bandgap Voltage Reference in 0.18 μm CMOS [J]. 2014.

[8] 张静. CMOS带隙基准源高阶温度补偿的设计与仿真[J]. 2013.

[9] 崔智军，王庆春. 基于不同VTH值的新型CMOS电压基准[J]. 2011.

[10] 刘鸿雁. 高精度CMOS带隙基准电压源电路设计[J].2014.

[11] 孙杰杰，张国俊. 利用MOS器件进行补偿的低温漂系数电压基准源[J]. 2013.

[12] 王永顺，井冰洁. 带有曲率补偿的高精度带隙基准电压源设计[J]. 2014.