应变调控单层氧化锌能带结构的第一性原理研究

汪志刚 曾祥明 张 杨 黄 娆 文玉华,*

(1乐山师范学院物理与电子工程学院, 四川 乐山 614004; 2厦门大学物理学系, 福建 厦门 361005;3西安交通大学应用物理系, 西安 710049)

应变调控单层氧化锌能带结构的第一性原理研究

汪志刚1,2曾祥明2张 杨3黄 娆2文玉华2,*

(1乐山师范学院物理与电子工程学院, 四川 乐山 614004;2厦门大学物理学系, 福建 厦门 361005;3西安交通大学应用物理系, 西安 710049)

采用基于密度泛函理论的第一性原理计算对单层ZnO薄膜能带结构的应变调控进行了研究. 计算结果表明: 沿着之字形方向的压缩应变和扶椅形方向的拉伸应变对薄膜带隙的调控都是线性的, 而且带隙调控的范围最大; 相反地, 在沿着之字形方向的拉伸应变和扶椅形方向的压缩应变的调控下, 带隙则呈现出非线性的变化. 对于双轴应变的拉伸与压缩, 带隙的变化都是非线性的. 这种通过不同的应变加载方式来实现对带隙不同程度的调控, 对ZnO薄膜在光学和催化等领域的应用具有重要的指导意义.

氧化锌; 应变; 能带结构; 第一性原理计算

WANG Zhi-Gang1,2ZENG Xiang-Ming2ZHANG Yang3HUANG Rao2WEN Yu-Hua2,*

(1College of Physics and Electronic Engineering, Leshan Normal University, Leshan 614004, Sichuan Province, P. R. China;2Department of Physics, Xiamen University, Xiamen 361005, Fujian Province, P. R. China;3Department of Applied Physics, Xi'an Jiaotong University, Xi'an 710049, P. R. China)

1 引 言

ZnO是一种直接宽禁带的半导体材料(常温时带隙Eg= 3.37 eV, 低温时Eg= 3.44 eV), 在常温常压下的最稳结构是纤锌矿结构. 它具有很大的激子结合能(60 meV)以及强压电、热电和发光等性质. 这些性质使得它被广泛地应用在电子器件、气体传感器、太阳能电池、紫外激光器等领域. 随着科学技术的进步, 不同的ZnO纳米结构如ZnO纳米薄膜、纳米线、纳米管、纳米带等均在实验上获得成功制备.1–4Freeman等5曾从理论上预言: 当ZnO薄膜的厚度接近于几个原子层时, 它将从体相的纤锌矿结构向石墨状的层状结构转变, 薄膜中层与层之间的相互作用将减弱, 而层内原子间的相互作用将增强. 随后, Tusche等6在Ag(111)衬底上生长出了2个单原子层厚度的ZnO(0001)薄膜. 他们通过表面X射线衍射和扫描隧道显微镜观察到这种薄膜的Zn和O原子位于同一平面, 形成了类似石墨状的平面六角结构, 并且随着薄膜厚度的增加, 这种平面六角结构将向ZnO体相的纤锌矿结构转变. 他们的结果从实验上证实了Freeman等的预测. 最近, Weirrum等7在Pd(111)衬底上制备出了石墨烯状的ZnO薄膜, 进一步验证了Tusche等的结果. 已有的理论计算研究均表明: 单层或多层的ZnO薄膜具有平面蜂窝状结构, 这种结构的稳定性主要来自于平面内Zn和O原子间强烈的sp2杂化.8–10

由上述可知, 单层ZnO薄膜是一个与石墨烯类似的二维材料. 目前, 有关单层ZnO薄膜的研究已有诸多报道, 研究内容涉及它的电子结构、磁性、力学和压电等性质. 例如, Tu9计算了ZnO单层薄膜的弹性、压电、电子结构和光学性质. Zheng11和Wang12等报道了本征缺陷对单层ZnO薄膜磁性的影响, 他们发现Zn空位诱导的自旋极化将使得它表现出铁磁性. Kan等13报道了常温下半氟化的ZnO单层薄膜具有半金属铁磁性, 全氟化时这种铁磁性将消失. 已有研究表明: 施加应变是调控材料电子结构性质(如带隙、载流子迁移率)的有效途径, 实验上施加应变一般是先将材料沉积在一个可延展伸缩的基底材料上. 如果材料的电子性质可以通过应变来控制, 这种材料将在纳米电机械系统中具有潜在的应用价值; 如果这种材料是直接带隙, 那么它可被应用于纳米光机械系统; 如果应变能够强烈地改变材料的电子结构, 那么这种材料可被用作应力或应变传感器.

目前, 有关应变对ZnO纳米材料能带结构调控的研究也有诸多报道. 例如, Si和Pan14发现应变可以诱导ZnO之字形(zigzag)纳米带从半导体向金属转变. Zhang等的研究揭示了应变诱导ZnO纳米线15和纳米管16从直接带隙向间接带隙的转变. Behera和Mukhopadhyay17研究了平面内均匀的双轴应变对单层ZnO薄膜带隙的调控作用, 结果表明带隙与应变具有类似抛物线的关系. 然而, Behera等的工作仅考虑了均匀的双轴应变对ZnO薄膜带隙的影响, 对相关的微观机理如电子结构的变化却没有阐明, 而这些变化对ZnO薄膜的光学和催化性质都可能产生重要的影响. 鉴于ZnO薄层能带结构的应变调控具有重要的理论意义和实用背景, 本文中我们将采用基于密度泛函理论(DFT)的第一性原理计算研究不同类型的应变加载方式对单层ZnO薄膜电子能带结构的影响和作用.

2 计算方法与模型

本文采用基于密度泛函理论的第一性原理方法, 通过采用VASP (Vienna ab initio Simulation Package)程序包,18,19对应变调控单层ZnO薄膜的能带结构进行研究. 计算中选用投影缀加波(PAW)方法,20,21电子之间的交换关联能选用广义梯度近似(GGA)22下的PBE (Perdew-Burke-Ernzerhof)赝势;23布里渊区中使用Monkorst-Pack245 × 5 × 1的k网格点, k点数的选用满足在倒空间中k点分割小于0.3 nm–1; 平面波截断能为400 eV; 结构弛豫采用共轭梯度算法, 能量和力的收敛精度分别为1 × 10–5eVsupercell–1和0.05 eVnm–1; 在垂直于平面的Z方向上真空层厚度设为1.5 nm，从而避免由于周期性引入的层间相互作用; Zn的3d104s2和O的2s22p4作为价电子, 其他电子都作为芯电子. 计算中, 对平面波切断能及k点数目进行优化, 使得体系的总能收敛于1 meV.

压缩和拉伸应变是通过标度ZnO薄层平面内相互垂直方向上的晶格常数来实现的, 即标度之字形方向和扶椅形方向的晶格常数, 如图1所示. 这种方法已成功地应用于其他单层二维材料的应变研究.25–27本文考虑了三种应变加载方式: 双轴应变、沿之字形方向的单轴应变以及沿扶椅形方向的单轴应变. 对于不同应变值下的结构, 在保持超原胞尺寸不变的情况下充分弛豫至能量最低态. 本文中考虑了对称应变下的拉伸和压缩, 应变定义为应变加载方向的晶格常数与无应变时的平衡晶格常数之比，即通过公式ε = (a – a0)/a0来描述, 其中a0是没有应变时的最优晶格常数, a是不同应变时相对应的晶格常数; ε为正值表示拉伸应变, 反之则为压缩应变. 我们首先对单层ZnO薄膜进行了结构优化, 优化后的几何构型呈现出类似石墨烯的平面六角结构. 在选择应变范围时, 我们计算了较大的应变范围内(–0.2 < ε < 0.2)它们的几何构型, 结果表明在较大的压缩应变时ZnO薄膜被压缩成了不规则的褶皱结构, 这种结构完全破坏了它原有的对称性. 因此,本文把应变ε局限在–0.1到0.1的范围内, 应变步长设为0.02, 在平衡状态附近步长取为0.01. 为了区分不同方向的单轴应变, 把六角结构的超晶胞转变成四方结构, 如图1所示. x轴方向定义为之字形方向, y轴方向定义为扶椅形(armchair)方向. 双轴应变是通过对之字形和扶椅形方向的晶格常数同时进行标度,如图1(b)所示; 对于单轴应变, 仅对之字形(或扶椅形)方向的晶格常数进行标度, 而使扶椅形(或之字形)方向的晶格充分弛豫到能量最低状态, 如图1(c)和1(d)所示.

图1 单层ZnO的晶格结构Fig.1 Crystal structures of monolayer ZnO

3 结果与分析

在无应变的情况下, 通过对原子位置和晶格进行充分弛豫后, Zn和O原子处于同一平面上. Zn与O之间的键长为0.190 mm, 这与实验值(0.192 mm)6以及之前报道的理论计算值9,10,17符合得较好. 单层ZnO薄膜在双轴应变下的能带结构以及Zn和O的分态密度如图2所示. 由图可见, 在无应变下的单层ZnO薄膜是一个带隙为1.663 eV的直接带隙半导体材料, 价带顶和导带底都位于布里渊区的Γ点位置.这也与之前的理论计算结果是一致的.8,28,29众所周知, 由于DFT理论自身的缺陷, 采用GGA计算得到的带隙值往往偏低. 为此, 我们又采用了新杂化泛函HSE06计算了单层ZnO薄膜的带隙, 发现它的值为3.305 eV. 这与Tu等9采用GW方法计算的单层ZnO薄膜的带隙值(3.576 eV)比较接近. 虽然GGA方法计算的结果低估了ZnO的带隙值, 但是GGA方法依然能够较为准确地预测带隙变化的趋势.15,30,31由于HSE06和GW计算量大, 计算过程非常耗时, 而且本文主要关注的是带隙变化的趋势, 并不需要准确计算它的带隙值. 因此, 本文仍然采用了较为普遍而耗时低的GGA方法来研究应变对单层ZnO电子结构的影响. 从图2(a)的态密度(DOS)分布可知, 无应变下的单层ZnO薄膜的价带顶主要来自O-2p和Zn-3d轨道的贡献, 而导带底则主要是由Zn-4s和O-2s所贡献. 当施加双轴压缩应变时, O-2p和Zn-3d态的耦合作用增强, 价带能级变得更宽, 如图2(b)所示;从–2到0 eV的能量区间内, O-2p和Zn-3d的态密度几乎重合; 由于强烈的耦合作用, O-2p态的局域性大为降低. 因此双轴压缩后, Zn和O原子的共价性增强, 离子性减弱. 另一方面, 拉伸应变则使得O-2p和Zn-3d态的耦合作用减弱, 电子的分布更加局域化,价带顶主要由O-2p所贡献, 如图2(c)所示; 同时, Zn-4s与O-2s相互作用减弱, 导带底主要由Zn-4s所贡献,此时, Zn和O原子的共价性减弱, 而离子性增强. 值得注意的是, 无论是压缩和拉伸应变, 单层ZnO薄膜的直接带隙性质并未改变, 价带顶和导带底均处于布里渊区的Γ点处. 与双轴应变相比, 单轴应变由于改变了ZnO薄膜的六角对称性, 能带的简并度大为降低.

图3给出了单层ZnO薄膜的带隙随应变的变化关系. 由图3可知, 带隙在双轴应变的调控下带隙呈现了明显的非线性变化: 在双轴的压缩应变下, 带隙先从1.663 eV增加到1.668 eV, 再从1.668 eV单调递减到1.352 eV; 带隙的最大值出现在ε = –0.01左右. Behera和Mukhopadhyay17计算的结果是在无应变状态下对应的带隙最大. 能带的这种差别可能是由于他们选取的应变间隔较大造成的. 相反地, 在双轴的拉伸应变下, 带隙表现出单调递减, 即从1.663 eV连读地减小到1.274 eV. 另外, 对于相同大小的压缩或拉伸应变, 带隙变化幅度的趋势与Behera和Mukhopadhyay17计算的结果不同, 通过与我们用局域密度近似(LDA)计算结果的对比发现,这种不同的趋势主要是来自于交换关联泛函的影响. 需要指出的是, 不论是双轴拉伸还是压缩, 对带隙的调控均表现出单调递减和不对称性; 也就是说,对于相同大小的双轴压缩和拉伸应变, 带隙的变化是不同的. 这与O-2p和Zn-3d态贡献的局域化程度强弱是直接相关的. 此外, 在所研究的应变变化范围内(–0.1 < ε < 0.1), 单层ZnO始终表现出直接带隙半导体的性质.

图2 双轴应变对单层ZnO能带结构和分态密度的影响Fig.2 Band structure and partial density of states of ZnO monolayer under biaxial strain

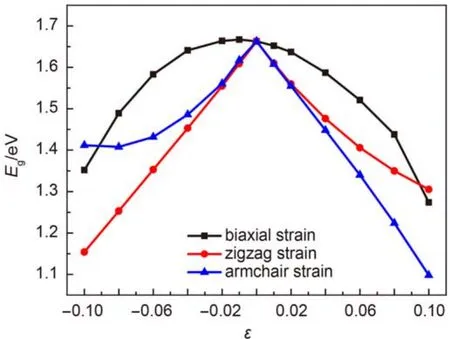
图3 单层ZnO在不同类型应变下的带隙Fig.3 Band gap of ZnO monolayer as a function of strain

对于其它两种类型的单轴应变(沿着之字形方向和扶椅形方向的单向应变), 无论是压缩还是拉伸应变, 随着应变的增加带隙的变化也都呈现出单调递减. 但是, 不同的应变其带隙变化的幅度和范围不尽相同. 沿之字形方向压缩或者沿着扶椅形方向拉伸时, 带隙与应变的关系都是线性的; 而沿之字形方向拉伸或者扶椅形方向压缩, 带隙的变化却都是非线性的. 对于之字形方向的单轴应变, 当ε从–0.1变化到0.1时, 带隙先从1.154 eV单调线性地增加到无应变时的最大值1.663 eV, 之后又非线性地降低到1.305 eV. 而扶椅形方向的应变ε从–0.1变化到0.1时, 带隙先从1.413 eV单调非线性增加到无应变时的最大值1.663 eV, 之后又线性地降低到1.098 eV.

通过比较不难发现: 对于三种不同形式的压缩应变, 当应变的幅度相同时, 之字形方向的单轴应变对应的带隙最低; 而对于三种不同的拉伸应变,当应变相同时, 扶椅形方向的拉伸应变对应的带隙总是最低. 也就是说, 在本文所考虑的应变范围内,当带隙与应变的关系是线性时, 应变对带隙的调控范围最大, 因此调控效果最好. 这种带隙随应变不同变化的原因可能与对称性有关. 均匀的双轴应变不会改变单层ZnO的六角对称性, 而施加两种不同方向的单轴应变时, 六角对称结构都会发生改变(见图1). 这种六角结构对称性的破坏与否, 将直接影响到O-2p和Zn-3d态对价带顶能级的贡献以及它们之间的耦合作用. 通过对比结构的变化发现, 之字形方向的压缩应变和扶椅形方向拉伸应变所对应的形状变化趋势是一致的, 因此它们对应的带隙变化亦是相同的(都是线性变化); 而之字形方向拉伸应变和扶椅形方向的压缩应变对应的形状变化趋势一致, 因此它们对应的带隙均为非线性变化. 此外,对于之字形方向的单轴应变, 在5%的应变范围内,它的泊松比约为0.67, 并随压缩应变的增大而减少,随拉伸应变的增大而增大. 而对于扶椅形方向的单轴应变, 在5%的应变范围内, 它的泊松比约为0.66,并随压缩应变的增大而增大, 随拉伸应变的增大而减少. 不同方向单轴应变时计算得到的泊松比虽然很接近, 但它们的变化趋势截然不同, 不仅证实了ZnO薄膜的各向异性性质, 也与沿两个方向施加应变时带隙变化的相反趋势相对应.

由图4的能量曲线可以看出, 相比单轴应变, 双轴应变下能量的变化更大, 尤其是双轴压缩应变,在ε = –0.1时能量的变化超过了10%. 这意味着实验上要实现这种应变比较困难. 而对于两种不同类型的单轴应变, 当应变绝对值达到10%时, 对应的能量变化都在2%以内. 这表明单轴应变所需要的能量更小, 因此实验上对于单轴应变的实现是有利的. 根据图4所示, 我们还看到, 能量的变化相对于应变的拉伸和压缩是不对称的. 对于双轴应变, 能量因压缩应变而升高的更加明显. 这种能量变化的不对称主要是由于形变后ZnO薄膜的结构对称性发生了变化. 这种现象在ZnO纳米线和纳米管中也出现过.12,13

图4 单层ZnO在不同类型应变下的能量变化Fig.4 Energy of ZnO monolayer as a function of strain

此外, 形变势可以被用来解释带隙和晶胞体积变化的关系.32正形变势表示带隙随晶胞体积的增大而减少, 而负形变势则恰好相反. 例如, 对于石墨烯状的单层BN(氮化硼), 它的π–π相互作用在调控带隙时起主导作用, 因此晶格膨胀使它们的带隙降低, 晶格压缩使带隙升高, 从而它具有正形变势.30对于单层ZnO薄膜, 无论是拉伸还是压缩应变都会使带隙降低, 这可能是由于ZnO薄膜同时具有π–π和σ–σ相互作用. 随着原子间距离的变化, 这两种相互作用对电子结构的影响方式不同;33在它们的相互竞争下, ZnO的形变势出现了反常行为. 本文的结果表明, 应变是降低ZnO薄膜带隙的有效方法. 这种应变对能带结构的调控如果能够通过实验来实现, 比如将ZnO薄膜的能带结构调控到与H2和O2的氧化还原势所对应, 那么对于它在光催化方面的应用将具有重要意义.

4 结 论

应变是一种有效地调控ZnO薄膜带隙的方法.本文研究了双轴应变和不同方向的单轴应变对单层ZnO薄膜带隙的影响和作用. 结果表明: 之字形方向的压缩应变和扶椅形方向的拉伸应变对带隙的调控是线性的, 且调控的范围最大, 引起的能量和体积变化较小, 在三种应变加载中对带隙的调控是最有利的. 此外, 在沿着之字形方向的拉伸应变, 扶椅形方向的压缩应变以及双轴的拉伸与压缩应变之下, 带隙均表现出非线性变化. 我们的研究结果对利用应变来调控ZnO薄膜的电子结构, 从而对它们在光学和催化中的实际应用具有重要的指导意义.

(1)Wang, Z. L. ZnO Bulk, Thin Films and Nanostructures; Elsevier: Oxford, 2006.

(2)Schmidt-Mende, L.; MacManus-Driscoll, J. L. Mater. Today 2007, 10 (5), 40. doi: 10.1016/S1369-7021(07)70078-0

(3)Wang, D. L.; Ruan, Y. F.; Zhang, L. C.; Yang, H. B. Acta Phys. -Chim. Sin. 2010, 26, 3369. [王丹丽, 阮永丰, 张灵翠,杨红波. 物理化学学报, 2010, 26, 3369.] doi: 10.3866/PKU. WHXB20101202

(4)Li, X. Q.; Fan, Q. F.; Li, G. L.; Huang, Y. H.; Gao, Z.; Fan, X. M.; Zhang, C. L.; Zhou, Z. W. Acta Phys. -Chim. Sin. 2015, 31, 783. [李湘奇, 范庆飞, 李广立, 黄瑶翰, 高 照, 范希梅, 张朝良, 周祚万. 物理化学学报, 2015, 31, 783.] doi: 10.3866/PKU.WHXB201502062

(5)Freeman, C. L.; Claeyssens, F.; Allan, N. L.; Harding, J. H. Phys. Rev. Lett. 2006, 96, 066102. doi: 10.1103/PhysRevLett. 96.066102

(6)Tusche, C.; Meyerheim, H. L.; Kirschner, J. Phys. Rev. Lett. 2007, 99, 026102. doi: 10.1103/PhysRevLett.99.026102

(7)Weirrum, G.; Barcaro, G.; Fortunelli, F.; Weber, F.; Schennech, R.; Surnev, S.; Netzer, F. J. Phys. Chem. C 2010, 114, 15432. doi: 10.1021/jp104620n

(8)Topsakal, M.; Cahangirov, S.; Bekaroglu, E.; Ciraci, S. Phys. Rev. B 2009, 80, 235119. doi: 10.1103/PhysRevB.80. 235119

(9)Tu, Z. C. J. Comput. Theor. Nanos. 2010, 7, 1182. doi: 10.1166/jctn.2010.1470

(10)Kang, J.; Zhang, Y.; Wen, Y. H.; Zheng, J. C.; Zhu, Z. Z. Phys. Lett. A 2010, 374, 1054. doi: 10.1016/j.physleta. 2009.12.031

(11)Zheng, F. B.; Zhang, C. W.; Wang, P. J.; Luan, H. X. Curr. Appl. Phys. 2013, 13, 799. doi: 10.1016/j.cap. 2012.12.008

(12)Qin, G. P.; Wang, X. Q.; Zheng, J.; Kong, C. Y.; Zeng, B. Comp. Mater. Sci. 2014, 81, 259. doi: 10.1016/j.commatsci. 2013.08.018

(13)Kan, E. J.; Xiang, H. J.; Wu, F.; Tian, C.; Lee, C.; Yang, J. L.; Whangbo, M. H. Appl. Phys. Lett. 2010, 97, 122503. doi: 10.1063/1.3491416

(14)Si, H.; Pan, B. C. J. Appl. Phys. 2010, 107, 094313. doi: 10.1063/1.3374684

(15)Zhang, Y.; Wen, Y. H.; Zheng, J. C.; Zhu, Z. Z. Appl. Phys. Lett. 2009, 94, 113114. doi: 10.1063/1.3104852

(16)Zhang, Y.; Wen, Y. H.; Zheng, J. C.; Zhu, Z. Z. Phys. Lett. A 2010, 374, 2846. doi: 10.1016/j.physleta.2010.04.069

(17)Behera, H.; Mukhopadhyay, G. Phys. Lett. A 2012, 376, 3287. doi: 10.1016/j.physleta.2012.09.038

(18)Kresse, G.; Hafner, J. Phys. Rev. B 1993, 47, 558. doi: 10.1103/PhysRevB.47.558

(19)Kresse, G.; Furthmuller, J. Phys. Rev. B 1996, 54, 10304. doi: 10.1103/PhysRevB.54.10304

(20)Blochl, P. E. Phys. Rev. B 1994, 50, 17953. doi: 10.1103/PhysRevB.50.17953

(21)Kresse, G.; Joubert, D. Phys. Rev. B 1999, 59, 1758.

(22)Perdew, J. P.; Chevary, J. A. Phys. Rev. B 1992, 46, 6671. doi: 10.1103/PhysRevB.46.6671

(23)Perdew, J. P.; Burke, K.; Ernzerhof, M. Phys. Rev. Lett. 1996, 77, 3865. doi: 10.1103/PhysRevLett.77.3865

(24)Monkhorst, H. J.; Pack, J. D. Phys. Rev. B 1976, 13, 5188. doi: 10.1103/PhysRevB.13.5188

(25)Gui, G.; Li, J.; Zhong, J. Phys. Rev. B 2008, 78, 075435.

(26)Zhang, C.; Sarkar, A. D.; Zhang, R. Q. J. Phys. Chem. C 2011, 115, 23682. doi: 10.1021/jp206911b

(27)Wong, J. H.; Wu, B. R.; Lin, M. F. J. Phys. Chem. C 2012, 116, 8271.

(28)Zheng, F. B.; Zhang, C. W.; Wang, P. J.; Luan, H. X. J. Appl. Phys. 2012, 111, 044329. doi: 10.1063/1.3688233

(29)Wang, Z. G.; Zhang, Y.; Wen, Y. H.; Zhu, Z. Z. Acta Phys. Sin. 2010, 59, 2051. [汪志刚, 张 杨, 文玉华, 朱梓忠. 物理学报, 2010, 59, 2051.]

(30)Yang, S.; Prendergast, D.; Neaton, J. B. Appl. Phys. Lett. 2011, 98, 152108. doi: 10.1063/1.3578193

(31)Yadav, S. K.; Ramprasad, R. Appl. Phys. Lett. 2012, 100, 241903. doi: 10.1063/1.4729153

(32)Chris, G.; Van de Walle, R. M. Phys. Rev. Lett. 1986, 62, 2028.

(33)Bhattacharya, A.; Bhattacharya, S.; Das, G. P. Phys. Rev. B 2011, 84, 075454. doi: 10.1103/PhysRevB.84.075454

First-Principles Study of Effect of Strain on the Band Structure of ZnO Monolayer

The effect of strain on the band structure of the ZnO monolayer has been investigated by firstprinciples calculations based on density functional theory. The results reveal that the band structure of the ZnO monolayer presents different dependences on three types of strain. The band gap linearly and steeply varies under uniaxial zigzag compressive strain and armchair tensile strain, while it shows nonlinear dependence on the other types of strain. Therefore, uniaxial zigzag compressive strain and armchair tensile strain should be the most effective to tune the band gap. This work has significant implications for application of strain to tune the optical and catalytic properties of ZnO nanofilms.

ZnO; Strain; Band structure; First-principles calculation

O641

10.3866/PKU.WHXB201506301

Received: March 24, 2015; Revised: June 29, 2015; Published on Web: June 30, 2015.

*Corresponding author. Email: yhwen@xmu.edu.cn.

The project was supported by the National Natural Science Foundation of China (10702056, 11204252) and Scientific Research Fund of Sichuan Provincial Education Department, China (12ZA072).

国家自然科学基金(10702056, 11204252)和四川省教育厅(12ZA072)资助项目

© Editorial office of Acta Physico-Chimica Sinica