基于试验模态的高速列车车体结构动力学模型修正研究

于金朋，张卫华，黄雪飞，肖守讷，张立民

（1.西南交通大学 牵引动力国家重点实验室，成都 610031；2.唐山轨道客车有限责任公司，河北 唐山 064000）

基于试验模态的高速列车车体结构动力学模型修正研究

于金朋1,2，张卫华1，黄雪飞2，肖守讷1，张立民1

（1.西南交通大学 牵引动力国家重点实验室，成都 610031；2.唐山轨道客车有限责任公司，河北 唐山 064000）

精确的有限元模型对于结构动态响应预测以及动态设计至关重要。利用模态试验数据，针对高速列车结构特点与动力学特性，深入分析设计空间方法选择、修正参数选择、响应面拟合和参数修正等关键问题，运用动力修正相关理论提出适合高速列车的基于试验模态车体动力学有限元模型修正方法。并运用该方法，采用模态试验数据修正高速列车车体结构的模态分析模型，频率的计算结果与试验结果的最大误差为-0.260 9%。研究验证基于模态试验数据高速列车车体动力学有限元模型的响应面修正方法的有效性。

振动与波；高速列车；有限元模型；模型修正；响应面

随着列车速度不断提高，车体所受到的载荷随之增大，且线路激励频率范围随速度提高而加宽；而车体轻量化水平的提高，车体的固有频率降低，使得车体产生较大的振动[1-3]。高速列车车体振动特性对乘车舒适性和结构安全性有重大影响，分析高速车体振动特性是高速列车车体设计与优化的重要内容[4,5]。由于车体结构复杂，目前，车体结构动力学性能分析主要采用有限元分析方法。

基于上述原因，精确的有限元模型对于结构动态响应预测以及动态设计至关重要。车体结构有限元模型通常基于真实结构做了较大的力学简化，导致车体动态性能的分析预测结果与实验结果存在一定的差别[6,7]。因此，较高质量的车体有限元模型是分析高速列车动态特性的关键。利用模态实验数据进行有限元模型修正可以获得较为精确可靠的有限元模型，也可获得模态试验中难以识别和响应模态[8]。

本文主要基于高速列车车体模态试验，采用响应面方法对车体结构动力学的有限元模型进行修正。

1 有限元模型修正思路

有限元修正首先要建立初始有限元模型，对未知参数进行初始设置，选择待修正的参数，通过有限元模型计算出理论值；同时，通过实验测试数据。在有限元模型修正过程中，要保证试验模态与计算模态是同一振型，具体做法为通过频率相关性并辅助振型相关性判断。修正过程是通过是计算值与试验值的差值最小化来调整未知参数，直到收敛为止。修正过程如图1所示。

有限元模型修正是在一定范围内，对有限元模型参数（如材料属性、几何参数、约束边界等）进行修正，减小有限元分析结果与试验结果之间的误差。有限元模型修正的技术已经广泛应用于工程结构振动性能分析、健康检测中[9,10]。有限元模型修正方法有基于矩阵型的修正方法、基于设计参数型的修正方法和基于响应面模型的有限元模型修正方法[11]。基于此，本文提出了基于模态试验高速列车车体动态特性的有限元模型的响应面修正方法，并以车体有限元模型修正为实例，验证该方法有效性。

2 基于响应面的有限元模型修正

基于响应面方法的有限元模型修正，是统计理论和模型修正技术的结合，其基本思想是：在有限次的有限元计算结果基础上，拟合得到结构响应与参数之间的显式函数关系式（响应面模型），并用此响应面模型代替有限元模型，实现结构模型参数的优化修正[12-14]。它克服了基于有限元模型和基于灵敏度分析中的不足，提高了计算效率。

响应面方法的有限元模型修正技术基本原理是：根据结构模态分析，选择适当的结构参数；在参数的设计空间内，计算样本点的响应；在此基础上，拟合得到结构响应与参数之间的响应模型；最后，以实测值为目标值，以响应面模型代替有限元模型进行修正参数的优化迭代，获得参数修正值及最准确的有限元模型[16,17]。

2.1 设计空间的方法选择

设计空间的方法选择与系统响应特性及其响应面函数形式密切相关，不同的设计方法适用于不同的系统及其响应面函数形式。正交设计和均匀设计仅适合于低阶响应面模型；BBD设计由于设计点数太多，不适宜于较大规模的模型；全因子法设计精度高，但计算量太大；D-最优设计方法用于大规模模型的高阶响应面建模，精度较高。常用的适宜于大模型精度较好是中心复合设计[10]。

中心复合设计用于响应面设计，可以回归拟合1阶、2阶或更高阶的模型。本文针对高速列车车体结构有限元模型修正的特点，采用中心复合设计法。

2.2 参数选择

方差分析是将求得样本数据中由各设计参数（因素）引起的偏差平方和和误差的偏差平方和，之后求出F值，运用F检测法进行假设检验[15]，判断出显著性参数。

F检测法数学表达式如式（1）所示

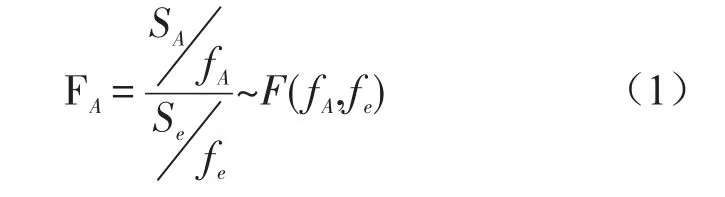
SA为因素引起的偏差平方和，Se为误差的偏差平方和，fA，fe分别因素A和偏差的自由度。

在给定显著水平α下，F检测法则为：

若F≥F1-a(fA,fe)，则认为设计参数A影响显著，否则不显著。

2.3 响应面拟合

响应面法是数学方法与统计方法结合的产物，在有限元模型修正中，假设系统的响应特征量y为因变量，为方差分析遴选出k个设计参数，则多项式响应面模型的形式如式（2）所示。

在有限元模型修正技术中，响应面模型精度直接影响模型修正的成功与否。响应面回归精度的检验原则如式（3）—式（5）所示[8]，符合要求则进行设计参数修正，若不符合要求，则重新进行实验设计。

yRS为一次响应面模型的计算值，y(j)为响应的有限元分析结果，代表有限元分析结果的平均值，N为设计空间上检验点的数量。

R2和RMSE均代表了响应面与有限元计算之间的差异程度，均在0和1之间。R2越接近于1，表明回归的响应面模型在设计空间内越能准确地描述系统输入与输出之间的关系；而RMSE则相反，越接近于0，表明模型越准确。

2.4 参数修正

基于响应面法的有限元模型修正，转化为基于参数修正的目标优化问题。目标函数如式（6）和式（7）所示。

xi代表设计参数，fa、fe分别是响应面值与试验结果。

3 高速列车车体有限元模型修正

3.1 车体模型

车体模型总长为24.12 m，车宽为3.2 m，车体高为3.6 m，车体几何模型如图2所示。

图2 车体几何模型

采用Ansys软件[9]建立壳单元Shell63有限元模型，弹性模量E=70 GPa，泊松比为0.3，密度为2 700 kg/m3，如图3所示。

图3 车体有限元模型

3.2 车体模态分析

计算车体结构前10阶在自由状态下的弹性模态，并将车体振型分为三种主要形式：Ⅰ型振动、Ⅱ型振动和Ⅲ型振动。

Ⅰ型振动主要包括车体的横弯、垂弯模态；Ⅱ型振动主要为呼吸模态；Ⅲ型振动主要包括菱形模态与扭转模态，表1为车体振型及频率计算误差。通过车体结构参数变化对车体振动模态的影响分析，识别了影响Ⅰ型振动和II型振动的主要结构参数，如表1所示。影响Ⅲ型振的主要结构参数为影响Ⅰ型振动和II型振动的结构参数综合。

表1 车体频率误差分类表

3.3 修正参数

根据车体结构特点和车体模态分析结果，车体有限元模型修正选择7个参数，记为A（ii=1,2…），如表2所示。优化参数Ai为无量纲化参数，用车体结构参数改变量的百分比表示。为了减少进入响应面模型的参数个数（Ai进入响应面模型），对车体相同部位、相同类型结构参数进行合并处理，如A3参数为车体参数C3、C4、C5、C6、C7的合并。优化后车体参数C3、C4、C5、C6、C7具有相同的改变量，用A3表示。优化参数A4也做相同处理。

每个参数取3个设计点，即7个因素，3个水平。采用正交设计，由L27(37)正交表确定27个计算样本点。对有限元分析获得的27组样本数据进行方差分析，取显著性水平a=0.05进行显著性检验，结果见表3。

表3 参数显著性检验

3.4 响应面函数拟合及响应面模型验证

将7个优化参数作为自变量，车体前10阶弹性频率作为因变量，采用模态频率相关性判断准则来评判计算频率ωt与实测频率ωa之间的相关程度，计算公式如式（8）所示。

MAC值介于0和1之间，如果模态完全相关，则MAC=1，如果完全不相关，则MAC=0，越接近1，则表明计算模态与实测模态相关性就越好。

有限元模型修正中常用完全二次多项式作为响应面模型拟合响应面函数，如式(9)所示。

其中xi,，xj为优化参数，β0,βi,βij为待定系数。这里i=7，x1，...，x7分别为优化参数C1，...，C7。

3.5 分析与试验的结果一致性

针对每1阶频率采用最小二乘法进行优化，优化函数如式（10）所示。

其中 f(x)ai为响应面模型计算的车体i阶频率，fei是车体第i阶试验频率，xi为优化参数，分别为优化参数的上下界。

优化前后的结果见表4，优化后的参数如表5所示。从表4可知，利用响应面进行单目标优化后车体前10阶的计算频率与实验结果比较，最大误差为-0.260 9%，表明该方法的有效性。

表4 优化结果

表5 优化后车体参数

4 结语

本文研究了高速列车车体动态特性的有限元模型修正的相关问题，主要包括修正参数选择、试验设计、构造响应函数、模态相关性判断和基于响应面模型的参数优化。运用该修正方法，采用实验数据修正了高速列车车体有限元模型，得到的初步结论如下：

（1）基于响应面法的有限元模型修正理论，提出了高速列车车体动态特性的有限元模型修正方法，频率误差最大为-0.2609%，验证了该方法的有效性；

（2）根据高速列车车体模态分析结果，提出了车体三种主要振型：梁式振动、板式振动和畸形振动，并依此确定了车体有限元模型的修正参数；

（3）利用提出的高速列车有限元模型修正方法，获得了计算精度较高的有限元模型，该方法可用于高速列车车体动态特性的有限元模型修正。

[1]佟维.高速铝合金客车的弹性振动分析[D].大连：大连交通大学，2008.

[2]吕永鑫.时速200公里电力机车车体结构优化设计[D].成都：西南交通大学，2008.

[3]万波.高速列车车体主要参数关系的研究[D].成都：西南交通大学，2009.

[4]任晋峰.高铁车辆车体振动基础性研究[D].大连：大连交通大学，2012.

[5]Gravitz S.I.An analytical procedure for orthogonalization of measured[J].MJAS,1958,25(11):1168-1173.

[6]刘太祥，龚兴龙，宗路航，等.高速列车车体结构振动和车内声学特性分析[J].噪声与振动控制，2013，33(3)：101-105.

[7]张启伟.桥梁结构模型修正与损伤识别[D].上海：同济大学，1999.[8]M.I.Friswell,J.E.Mottershead.Finite element method model updating in structural dynamics[J].Dordrecht: KluwerAcademic Publisher,1995.

[9]任伟新，陈华斌.基于响应面的桥梁有限元模型修正[J].土木工程学报，2008，12，41(12)：73-78.

[10]费国庆，张令弥，李爱群，等.基于统计分析技术的有限元模型修正技术研究[J].振动与冲击，2005，24(3)：23-26.

[11]郭勤涛，张令弥，费庆国.结构动力学有限元模型修正的发展—模型确认[J].力学进展，2006，36(1)：36-42.

[12]Batmaz I,Tunali S.Small response surface designs for metamodel estimation[J]. European Journal of Operational Research,2003,145(2):455-470.

[13]Romero V J,Swiler L P,Giunta A A.Construction of response surface based on progressive-lattice-sampling experimentaldesignswith application to uncertainty propagation[J].Structure Safety,2004,26(2):201-219.

[14]Rutherford B M,Swiler L P,Pae T L,et al.Response surface(meta-model) methods and applications[C]. Proceeding of the 24 th International Modal Analysis Conference.2006.

[15]王志江，陶靖轩，沈鸿.数理统计与概率论[M].北京：中国计量出版社，2004：149-169.

[16]程霄翔，费庆国，何顶顶，等.基于响应面的大型输电塔结构有限元模型动力修正[J].振动与冲击，2011，30(5)：116-122.

DynamicModelCorrectionofCar-bodyStructuresofHigh-speed TrainsBasedonExperimentalModals

YU Jin-peng1,2,ZHANG Wei-hua1,HUANG Xue-fei2, XIAO Shou-ne1,ZHAGN Li-min1
(1.State Key Laboratory of Traction Power,Southwest Jiaotong University,Chengdu 610031,China; 2.Tangshan Railway Vehicle Co.Ltd.,Tangshan 063035,Hebei China)

The precise finite element model for structure dynamic response prediction and dynamic design is very important.In this paper,using the modal test data,some key issues such as design space method selection,parameters selection,response function fitting,structure and parameters optimization etc.for the finite element model,were analyzed according to the structure characteristics and dynamic characteristics of high speed trains.The response surface correction method for the dynamic model of the car-body structure of the high-speed train was proposed based on the experimental modals.Using this method and the modal test data,the modal analysis model of the car-body structure was corrected.The maximum error of the frequency between the computation results and the test results is 0.260 9%.The effectiveness of the response surface correction method for dynamic FE model for the car-body structure of the high-speed train based on experimental modals was verified.

vibration and wave;high-speed train;finite element model;model correction;response surface

TH212；TH213.3

A

10.3969/j.issn.1006-1335.2015.03.016

1006-1355(2015)03-0073-05+168

2015－01－17

“：十二五”国家科技支撑计划项目(2013BAG24B02-1)

于金朋（1979－），男，河北唐山人，高级工程师，博士研究生。主要从事列车系统集成技术及车辆动态设计。E-mail:451340185@qq.com