层状岩体各向异性弹塑性本构模型的数值实现

高敏，贾善坡，刘晓东，张力伟，舒婧曦 （长江大学城市建设学院，湖北荆州434023）

层状岩体在物理、力学特性上较均质岩体具有更显著的各向异性、非线性及非连续性，其变形与破坏性质十分复杂。国内外学者对层状岩体的各向异性特征及本构关系进行了大量研究。Jeager［1］和Tien等［2，3］开展了大量的理论与试验研究，这些研究成果为层状岩体本构模型的进一步研究奠定了基础。文献 ［4～6］在横观各向同性理论与岩石材料各向异性理论的基础上，通过试验测定了横观各向同性体的5个弹性参数，并建立了岩体的弹性模量与泊松比随节理面倾角变化的函数关系，实现了层状岩体等效弹性参数的各向异性特征。贾善坡等［7］在考虑结构面的几何特性和力学性质的基础上建立了岩体各向异性本构模型。黄书岭等［8］在考虑一组节理面的层状岩体复合材料模型的基础上，建立了考虑多组结构特性的层状岩体多节理本构模型。虽然众多学者做了大量研究工作，但是目前将层状岩体的弹性与塑性的各向异性特征在有限元软件中实现的研究较少。下面，笔者在ABAQUS自带节理材料模型的基础上，结合岩体各向异性弹性参数的研究成果，利用ABAQUS中USDFLD子程序接口，采用FORTRAN语言进行开发并嵌入到ABAQUS软件中实现非线性计算功能，通过实际算例分析验证了该模型的有效性和可靠性。

1 层状岩体各向异性弹性参数研究

相关学者［4～6］在岩石横观各向同性理论和岩石材料的各向异性理论的基础上，通过试验测定了横观各向同性体的5个弹性参数，并建立了岩体的弹性模量和泊松比随节理面倾角变化的函数关系。

Amadei［9］认为，含层理面的岩石应力（σx，σy，σz，τyz，τzx，τxy）与应变（εx，εy，εz，γyz，γyx，γxy）的关系如下：

由各向异性理论可知，轴向应力σy与应变（εx，εy，εz）存在如下关系：

式中，a12、a22、a23是由层理面倾角θ和5个弹性参数E1、μ1、E2、μ2、G2决定的函数关系式，其表达式分别为：

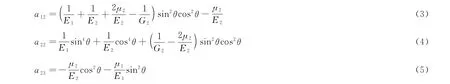
式中，E1、μ1分别为平行于横观各向同性面的弹性模量与泊松比；E2、μ2、G2分别为垂直于横观各向同性面的弹性模量、泊松比和剪切模量。上述5个弹性参数可以通过岩体的单轴及三轴压缩试验测得。

只要确定了5个弹性参数E1、μ1、E2、μ2、G2，即可确定任一节理面倾角的弹性参数E和μ，即：

这样就可以得到节理岩体弹性模量与泊松比随层理面倾角θ变化的函数关系式：

2 子程序开发步骤

在ABAQUS自带节理材料模型的基础上，结合层状岩体弹性参数的各向异性，以FORTRAN语言为平台，开发了本构模型子程序，以ABAQUS软件为求解器使该模型可以进行数值计算，进而用于工程实践中。

子程序的开发主要包括以下4个部分：确定层状岩体5个等效弹性参数；调用每一步计算结果的应力矩阵；调用每一步计算结果最大主应力方向的余弦值；将式（7）的函数关系嵌入子程序，其中式（7）中的θ是表示在试验过程中改变的节理面的倾角，其余弦值与实际工程中最大主应力的方向余弦值是对应的，最大主应力方向余弦值在ABAQUS软件中通过调用SPIND函数得到。

数值计算步骤如下：利用ABAQUS自带节理材料模型，在初始条件和初始弹性参数下进行初始增量步计算，并利用计算结果以及调用开发的子程序计算得到新的弹性参数，再利用新的弹性参数进行下一增量步计算，以此循环直至所有计算步骤完成（见图1）。

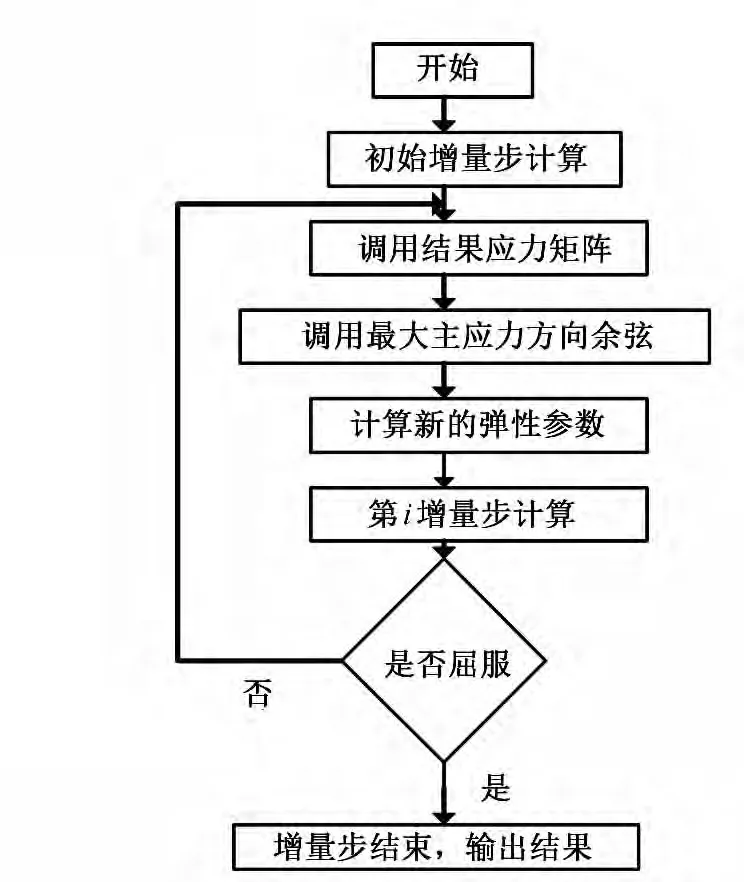
图1 程序计算步骤

3 数值算例

3.1 算例模型

选取某岩质边坡进行数值试验（具体尺寸见图2）。边坡右侧和坡脚下左侧均为竖向滑动水平约束边界条件，底面为全部固定边界。土体容重γ＝25kN／m3，粘聚力c＝0.05MPa，内摩擦角φ＝45°。弹性模量E1＝37.79GPa，E2＝24.39GPa，泊松比μ1＝0.254，μ2＝0.180，剪切模量10.85GPa［6］。

3.2 计算工况

1）工况1 对比分析各向同性弹性模型与各向异性弹性模型计算结果的差异性，各向同性弹性模型弹性模量与泊松比分别取为E1＝37.79GPa、μ1＝0.254，各向异性弹性参数按式（7）选取。

2）工况2 对比分析ABAQUS自带节理材料模型与各向异性弹塑性模型的计算结果，弹性参数的选取同工况1，其中节理面倾角θ从0～90°变化。

3）工况3 选取文献 ［6］中层状岩体弹性参数E和μ随节理面倾角θ变化的试验结果，与各向异性弹塑性本构模型计算结果得到的弹性参数E和μ进行对比分析。

3.3 计算结果分析

1）工况1计算结果分析 工况1计算结果如图3所示。对比各向同性弹性计算结果与各向异性弹性结算结果可知，图3（a）与图3（c）的Mises应力图分布大致相同，但是图3（c）中在边坡角处存在着变化的不均匀性；图3（b）与图3（d）中的位移云图分布差异较大，且图3（d）图的变化更能体现出位移变化的不均匀性，这说明各向异性弹性数值模型能够在一定程度上反映出各向异性特征。

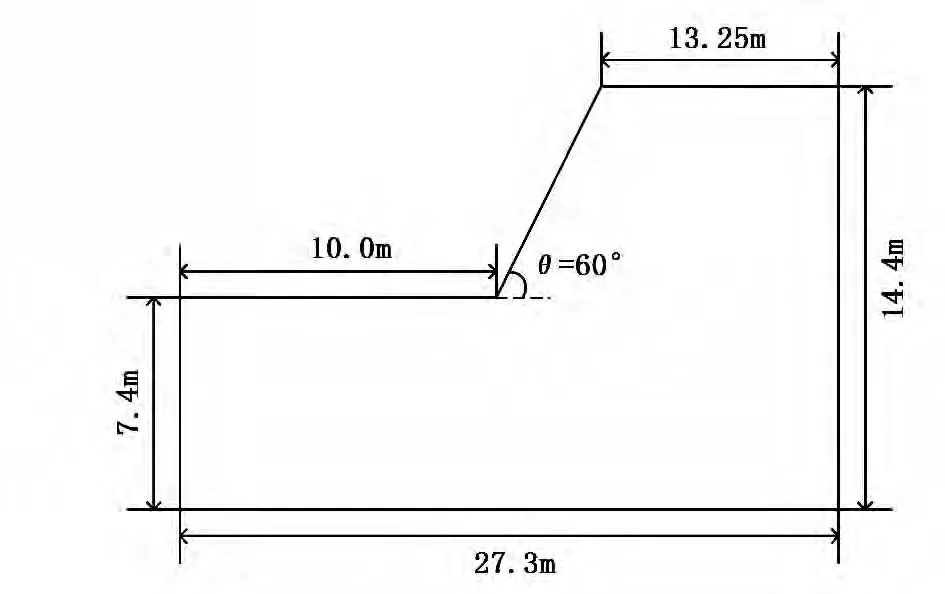
图2 计算模型尺寸图

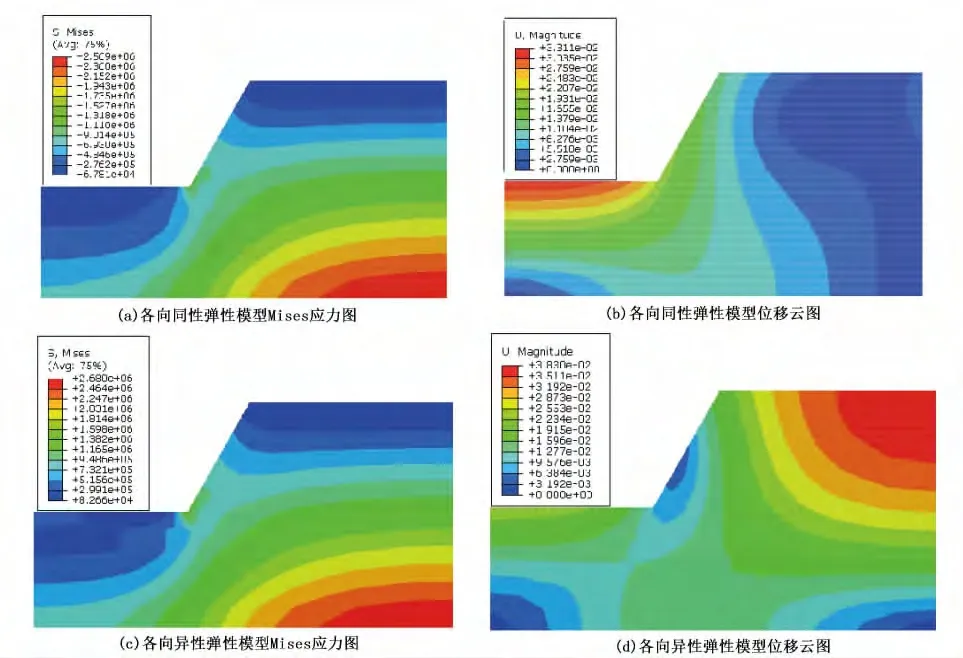
图3 工况1计算结果图

2）工况2计算结果分析 图4所示为ABAQUS自带节理材料模型计算结果（节理面倾角θ从0～90°变化，其中选取10、30、60、80°的计算结果）。从图4可以看出，随着节理面倾角的变化其Mises应力与位移变化不大，且云图分布比较均匀；塑性破坏区域呈现出先增大再减小再增大的趋势，且塑性破坏区域变化不均匀，呈现出一定的各向异性特征。

图5所示为选取层状岩体各向异性弹塑性本构模型计算结果（节理面倾θ从0～90°变化，其中选取10、30、60、80°计算结果）。对比各向异性弹塑性模型与ABAQUS自带节理材料模型计算结果可知，塑性破坏区与Mises应力云图差异不大，但各向异性弹塑性数值模型计算的结果偏大，特别是位移云图的分布具有明显的不均匀性。上述分析表明，各向异性弹塑性数值模型能够在一定程度上准确表现出岩石材料的各向异性特征。

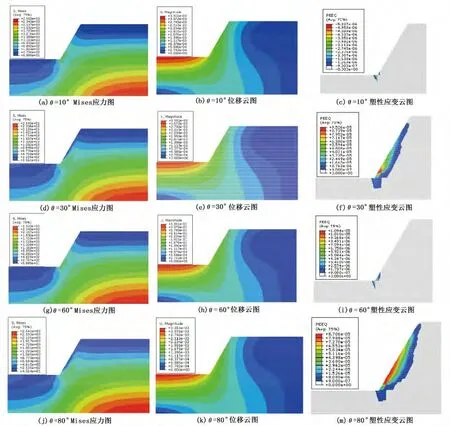
图4 ABAQUS自带节理材料计算结果图

3）工况3计算结果分析 通过数值计算得到的E和μ随节理面倾角θ变化的结果与文献 ［6］中试验得到的结果对比如图6所示。从图6可以看出，通过数值计算得到的弹性模量E随节理面倾角的变化与试验值比较接近且变化规律具有一致性，随着节理面倾角θ的增加而增加。另外，虽然通过数值计算得到的泊松比μ与试验值有一定的误差，但是也随着节理面倾角θ的增加而增加。

4 结语

在ABAQUS自带节理材料模型基础上，结合层状岩体弹性参数的各向异性研究，采用FORTRAN语言编制了本构子程序，使层状岩体各向异性弹塑性模型得以数值实现。以某岩质边坡为数值算例，采用多种工况对比分析，验证了层状岩体各向异性弹塑性数值模型的可靠性，从而为实际工程中研究层状岩体的各向异性特征提供数值计算基础。层状岩体各向异性弹塑性数值模型虽然能够反映岩体的各向异性特征，但是如何考虑多组节理面存在并将其运用到复杂模型及实际工程中有待今后进一步的研究。

图5 各向异性弹塑性本构模型计算结果

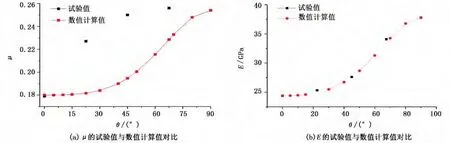
图6 工况3计算结果对比

［1］Jaeger J C.Shear failure of anisotropic rocks ［J］.Geology Magazine，1960，97（1）：65～72.

［2］Tien Y M，Kuo M C.A failure criterion for transversely isotropic rocks ［J］.International Journal of Rock Mechanics and Mining Sciences，2001，38（5）：399～412.

［3］Tien Y M，Kuo M C，Juang C.An experimental investigation of the failure mechanism of simulated transversely isotropic rocks ［J］.International Journal of Rock Mechanics and Mining Sciences，2006，43（8）：1163～1181.

［4］席道英，陈林 .岩石各向异性参数研究 ［J］.物探化探计算技术，1994，16（1）：16～21.

［5］张学民 .岩石材料各向异性特征及其对隧道围岩稳定性影响研究 ［D］.长沙：中南大学，2007.

［6］刘运思，傅鹤林，伍毅敏，等 .横观各向同性岩石弹性参数及抗压强度的试验研究 ［J］.中南大学学报（自然科学版），2013，44（8）：3398～3404.

［7］贾善坡，邹臣颂，吴渤，等 .考虑岩体各向异性强度的隧洞围岩稳定性分析 ［J］.防灾减灾工程学报，2013，33（2）：179～184.

［8］黄书岭，丁秀丽，邬爱清，等 .层状岩体多节理本构模型与试验验证 ［J］.岩石力学与工程学报，2010，29（4）：743～756.

［9］Amadei B.Importance of anisotropy when estimating and measuring in situ stresses in rock ［J］.International Journal of Rock Mechanics and Mining Sciences，1996，33（3）：293～325.