一种桁架结构优化的萤火虫算法改进研究

李彦苍，于洋，王杰 （河北工程大学土木工程学院，河北 邯郸056038）

随着国民经济的不断增强和综合国力的不断进步，在城市建设过程中建筑结构形式的多样化为城市带来了诸多现代化的元素。建筑结构体系随之也越来越复杂，设计过程中面临着影响因素多、设计计算工作量大等问题。因此，设计出的建筑结构往往存在着诸多问题，达不到应有的设计标准，遭到破坏的情形时有发生，对我国国民宝贵的财产和人身安全会造成不可预测的伤害，所以对结构优化设计的实验和探索具有重要意义［1，2］。

结构优化是指在限定的条件下，使结构的某些性能表现最优。柳春光等根据投资－效益准则，提出了基于遗传算法的全寿命抗震性能的海桥梁结构多目标优化设计方法［3］；杨继超等针对工程结构承受扰动载荷，最优解难以准确获得的问题，对刚架体结构稳健优化设计方法进行了相关研究［4］；王晓军等提出了一种基于非概率凸模型可靠性的结构优化设计方法并取得相关结论［5］；Mohammed Jameel等提出了一种对高层建筑及其负载作用下的造型结构优化设计方法［6］；Sabouri－Ghomi S等调查研究了每个组件的刚度、强度对结构整体的强度、刚度的影响并提出其进行优化设计的方法［7］；Giuseppe等提出了一种基于微分金华算法并将其应用在预应力混凝土梁的优化设计中，取得了显著成果［8］；AndréTeófilo Beck等对确定性、可靠性和基于风险的不确定性条件下的结构优化进行对比研究取得了相关结论［9］。以上研究均推动了结构优化设计的研究和发展，但如何克服优化过程中存在着控制目标多、目标量化难和计算复杂等难题仍需进一步深入研究。

2008年，剑桥学者Yang Xinshe提出了一种全新的群智能仿生优化算法：萤火虫算法（Firefly Algorithm，简称FA）［10］。该算法通过模拟野生环境中萤火虫在觅食、寻偶和警戒等过程中发出荧光的现象而来的，是基于智能群体的随机非线性搜索优化算法，广泛应用于模式识别、网络路由选择、自动控制、组合优化、机器人路径规划以及社会科学等多个领域［11］。

笔者尝试将萤火虫算法引入到桁架结构的优化设计过程中，同时针对该算法存在的缺陷，对其进行适当改进，以期待解决优化设计后期控制目标多、计算复杂、收敛速度慢和收敛精度低等问题。

1 桁架结构的形状优化模型

各节点坐标和各杆件截面面积是结构形状优化设计的关键问题［12］，也是建立数学模型的关键变量，综合考虑这2点因素才能得到最优解。因此，以桁架结构的总重量为目标函数，以节点位移、应力和稳定性为约束条件，已知结构的基本设计参数（材料密度、最大应力、截面形状、弹性模量、剪切模量和最大位移等）建立数学模型。

设计变量：

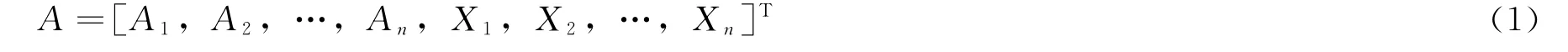
式中，Ai为杆件的截面面积；Xi为杆件的节点坐标；n为杆件的组数。目标函数：

式中，f（x）为结构的重量；ρi为材料密度；Ai为截面面积；Li为第i组杆件的长度。约束条件包括：

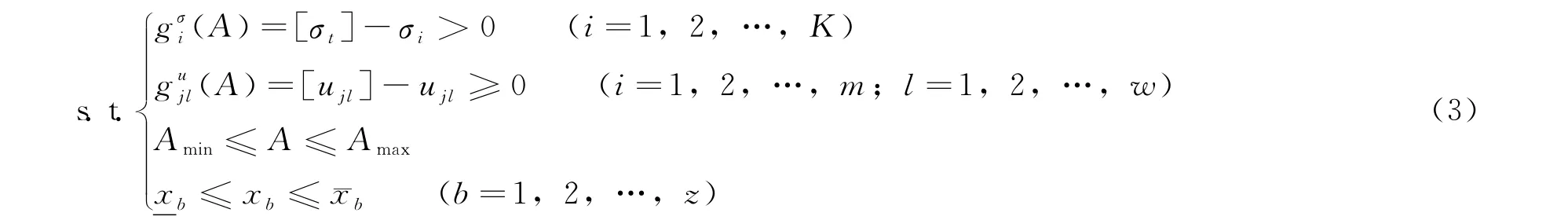
式中，（A）为应力约束；（A）为位移约束；K为总的杆件数；σt为最不利应力； ［σt］为容许应力；ujl为节点j在方向l上的最不利位移；［ujl］为节点j在方向l上的容许位移；m为节点总数；w为节点位移约束的维数；Amin为杆件截面积的下限；Amax为杆件截面积的上限；为第k坐标的下限；为第k坐标的上限；z为节点变量数。

2 改进的萤火虫算法

自身亮度和吸引度是萤火虫彼此间的吸引能力的2个关键因素［13］。其中，每一个萤火虫所在的位置都代表了一个目标初始解，该位置决定该萤火虫发出的荧光亮度，位置越好亮度越高，目标值越佳。每个萤火虫的吸引度与其自身的荧光亮度相关，越亮吸引度越大，较暗的萤火虫会自发的向较亮的萤火虫方向移动，同时吸引度会随彼此间距离的增加而减小；若亮度相同，则随机移动。算法的数学描述如下。

荧光亮度：

式中，I0为萤火虫的最大荧光亮度；γ为光强吸收系数，一般为常数；rij为萤火虫i和j之间的空间距离。

吸引度为：

式中，β0为最大吸引度。

位置更新公式：

式中，xi、xj为萤火虫i和j的所在位置；α为步长因子，一般为常数，且在［0，1］之间取值；rand为［0，1］上服从均匀分布的随机因子。

萤火虫算法虽然在全局寻优的问题上具有很大的优势，但算法自身也存在着一些不可忽视的缺陷：对初始解的分布具有较强的依赖性、易于在早期发生停滞、求解结果精度低和后期收敛速度缓慢等［14，15］。

为了避免FA出现停滞现象，减少陷于局部最优的可能，因此，在萤火虫位置的初始化时，利用Logistic方程（7）对初始解群进行分布：

式中，Xk为映射到［0，1］区间的变量；μ为控制参数。

设置最大迭代次数Np，进行全局搜索，针对全局最优解，依式（8）：

作高斯扰动。其中，NGbest为扰动后的位置。

然后依式（9）求最终最优解Gbest：

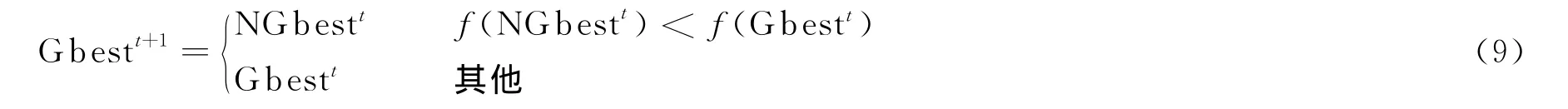
寻优流程如图1所示。

3 实例应用

图2所示为37杆桁架桥结构，长10m，高1m，杆件各节点坐标如表1所示。现假设下弦各节点受到垂直向下的节点荷载（P＝10kN）作用，且已知横架桥结构的对称性在荷载作用和优化的过程中不变，节点10的竖向位移最大值为10mm，各连接杆材料相同且同为圆杆，弹性模量E＝220GPa，密度ρ＝7900kg／m3，最小截面积为60mm2，允许应力σcr为265MPa。

依实例，建立目标函数，在已知相关基本参数的条件下建立满足强度、刚度和稳定性等条件的约束方程。应用改进的萤火虫算法对其进行优化，步骤如下：

Step 1 依实例初始化：m为萤火虫种群个体数量，N为萤火虫种群规模，γ为荧光强度吸收系数，β0为萤火虫最大吸引度，maxT为迭代阀值；

Step 2 萤火虫位置初始化：选择综合表现优秀的萤火虫个体设定为实践案例中可行解空间的初始个体；

Step 3 由式（4）变新荧光亮度；式（5）变新吸引度；式（6）变新位置；

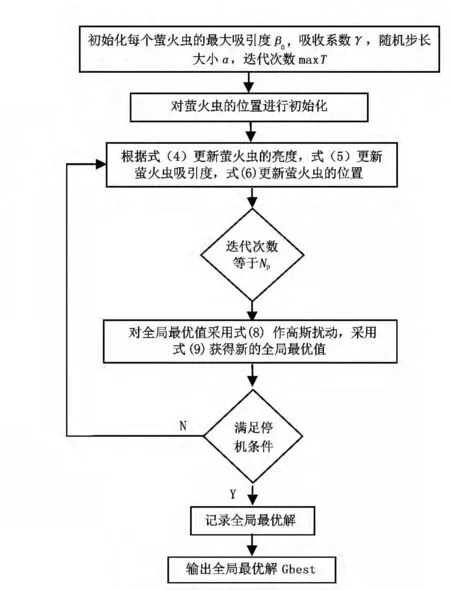
图1 算法的流程图

Step 4 由式（8）对局部最优值做高斯扰动，式（9）求出的全局最优值；

Step 5 如果满足停机准则，则停止；否则转入Step 3，进行下一循环继续寻优，迭代次数＋1；

Step 6 输出Gbest且结束算法。

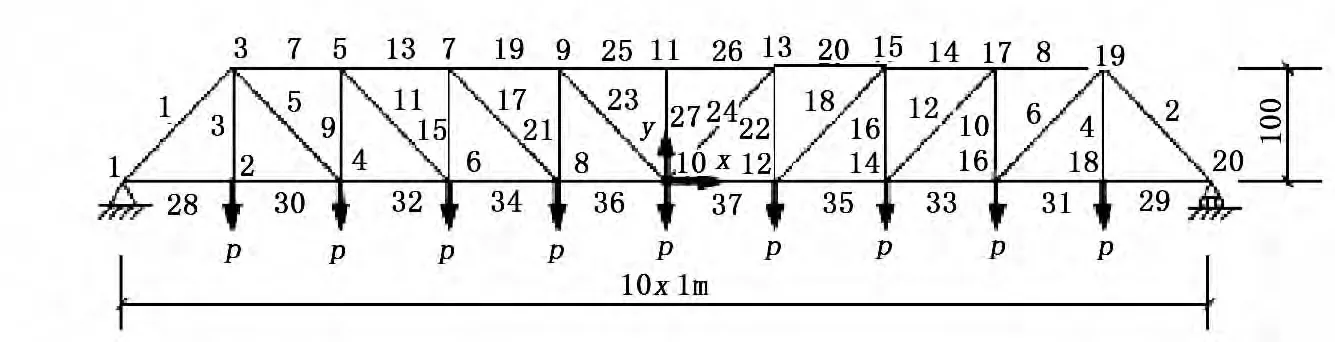
图2 桁架的初始设计

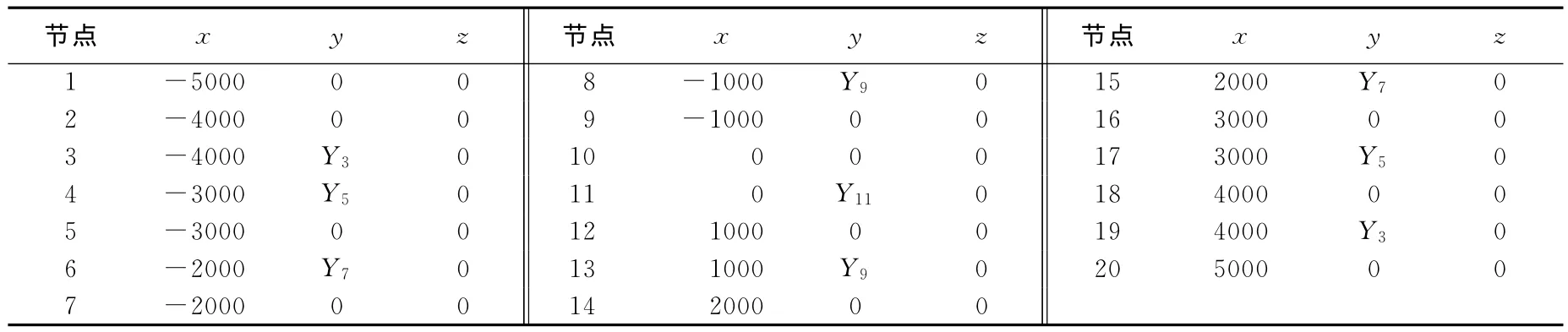
表1 37桁架杆各节点坐标

局部稳定性约束为：

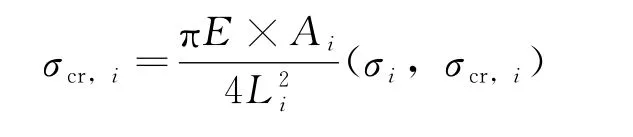
设计变量：

优化结果见表2，优化形状见图3。

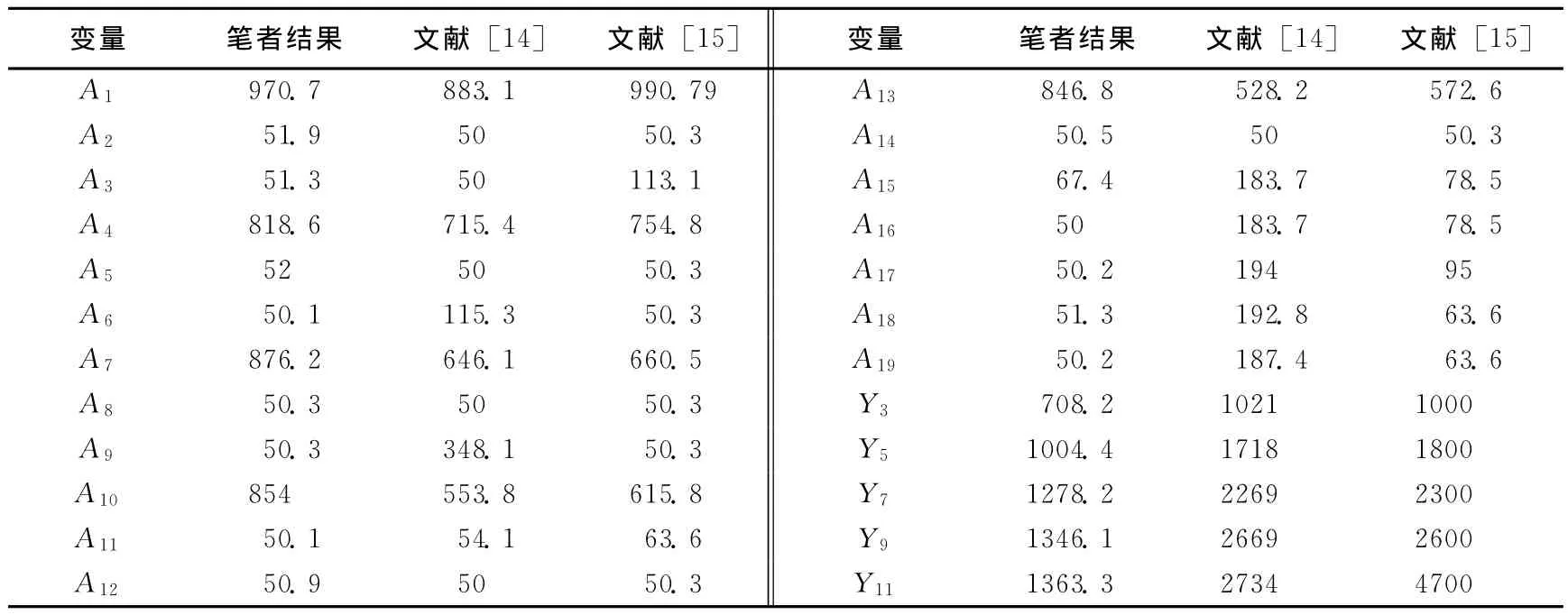
表2 37杆桁架桥形状优化结果比较

由表2和图4可知，改进的萤火虫算法经过大约350次迭代，曲线己无限接近收敛值，且结果优于其他算法。

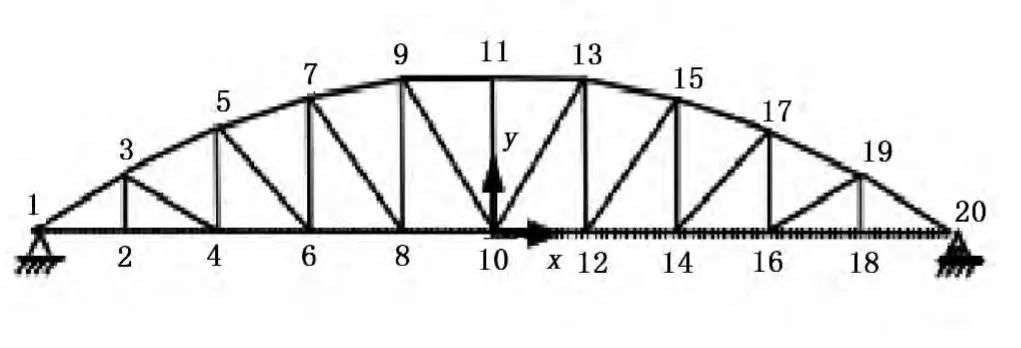
图3 形状优化结果

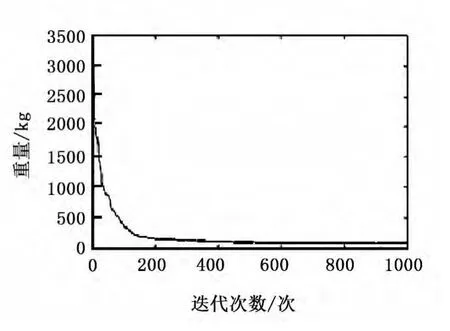
图4 迭代次数

4 结语

笔者基于结构优化的相关理论，结合37杆桁架桥结构案例，建立了桁架桥结构的数学模型，引入萤火虫算法并采用Logistic方程和高斯干扰对其改进，利用改进后的萤火虫算法对37杆桁架桥结构的数学模型进行了优化计算，该研究为结构优化设计提供了一种新的思路和方法。

［1］宋述芳，吕震宙 .基于高阶矩的稳健优化设计研究 ［J］.力学学报，2012，44（4）：735～744.

［2］张瑞军，邱继伟，贾庆轩 .基于灵敏度附加项的多目标可靠性稳健优化设计 ［J］.应用基础与工程科学学报，2013，21（4）：777～785.

［3］柳春光，张士博，柳英洲 .基于全寿命抗震性能的近海桥梁结构多目标优化设计方法 ［J］.大连理工大学学报，2015，55（1）：39～46.

［4］杨继超，戴宗妙 .不确定载荷下刚架体结构稳健优化设计 ［J］.哈尔滨工程大学学报，2015，36（5）：1～6.

［5］王晓军，王磊，贾晓 .基于非概率凸模型可靠性的结构优化设计 ［J］.北京航空航天大学学报，2012，38（5）：630～635.

［6］Mohammed Jameel1，Saiful Islam A B M，Raja Rizwan Hussain，et al.Optimum Structural Modelling for Tall Buildings［J］.The Structural Design of Tall and Special Buildings，2013，22：1173～1185.

［7］Sabouri－Ghomi S，Payandehjoo B.Investigating the effect of stiffness and strength of each component on overall stiffness and strength of yielding damped braced core（YDBC）［J］.The Structural Design of Tall and Special Buildings，2011，20（7）：747～756.

［8］Giuseppe Quaranta，Alessandra Fiore，Giuseppe Carlo Marano.Optimum Design of Prestressed Concrete Beams Using Constrained Differential Evolution Algorithm ［J］.Structural and Multidisciplinary Optimization，2014，49（3），441～453.

［9］AndréTeófilo Beck，Wellison Joséde Santana Gomes.A Comparison of Deterministic，Reliability－Based and Risk－Based Structural Optimization Under Uncertainty ［J］.Probabilistic Engineering Mechanics，2012，28：18～29.

［10］Yang Xinshe.Firefly Algorithms for Multimodal Optimization ［A］.SAGA’09：Proceedings of the 5th International Conference on Stochastic Algorithms：Foundations and Applications ［C］.Berlin：Springer－Verlag，2009：169～178.

［11］Fister Iztok，Fister Jr.Iztok，Yang Xinshe，et al.A Comprehensive Review of Firefly Algorithms［J］.Swarm and Evolutionary Computation，2013，13：34～46.

［12］张成，吴慧，高博青 .非概率不确定性结构的鲁棒性分析 ［J］.计算力学学报，2013，30（1）：51～56.

［13］Rahmani A，Mirhassan S A.A Hybrid Firefly－Genetic Algorithm for the Capacitated Facility Location Problems［J］.Information Sciences，2014，238：70～78.

［14］Gandomi A H，Yang Xinshe S，Talatahari A H.Alavi，Firefly Algorithm with Chaos［J］.Commun Nonlinear Sci Numer Simulat，2013，18：89～98.

［15］Yang Xinshe，DEB S.Eagle Strategy Using Walk and Firefly Algorithms for Stochastic Optimization ［J］.Studies in Computational Intelligence，2010，284：101～111.

［16］李丽娟，黄志斌，刘锋 .启发式粒子群优化算法及其在空间结构优化中的应用 ［J］.空间结构，2008，14（3）：47～55.

［17］王栋，张卫红，姜节胜 .桁架结构形状与尺寸组合优化 ［J］.应用力学学报，2002，19（3）：72～76.