大型船舶推进轴系扭振特性仿真和试验

谈微中，张 聪，田 哲，严新平，胡木水

(1.武汉理工大学 能源与动力工程学院 可靠性工程研究所，湖北 武汉430063;2.武汉理工大学 船舶动力工程技术交通行业重点实验室，湖北 武汉430063)

0 引 言

动力装置作为船舶的动力核心，其重要性不言而喻。而船舶推进轴系作为连接主机与螺旋桨的主要部件，将前者所产生扭矩传递给后者，同时将螺旋桨产生的轴向推力通过推力轴承传给船体，以推动船舶运动［1］。在船舶航行过程中，轴系会产生不同方向的振动，其中由柴油机产生的周期性激振力矩以及螺旋桨传递的随机性阻力力矩导致的船舶轴系扭转振动是其中极其重要的一个组成部分。若扭转振动过大可能导致断轴、轴承损坏，扭转振动的大小直接关系到船舶的航行性能和安全性，所以对船舶推进轴系的扭转振动特性进行分析和研究，具有十分重要的意义［2－4］。

以往对船舶推进轴系的振动特性进行研究时，大多情况下采用基于集中质量系统的计算分析法［5］。该方法对于简单结构零件的运动规律的描述具有一定的准确性，然而，船舶推进轴系工作状态的复杂性加上轴系振动与船体变形的耦合，基于集中质量系统的计算分析法难以准确描述轴系及其部件的振动响应规律。基于有限元理论和多体动力学的刚柔耦合计算机仿真，随着计算机技术的发展已逐渐成为研究轴系振动的新方法。这种方法在车辆及发动机设计及仿真计算等方面已有广泛的应用［6－7］，但在船舶推进轴系，尤其是轴系振动方面应用较少。一方面，船舶推进轴系工作环境比较复杂，边界条件及影响因素不易确定;另一方面，船舶推进轴系结构比较复杂，从柴油机曲轴、推力轴承、中间轴一直到尾轴及螺旋桨，组成部件较多，建模和计算工作量较大［8］。因此，目前从事这方面的研究工作较少。

本文采取基于多体动力学和有限元理论相结合的方法建立刚柔耦合模型，对大型船舶推进轴系的振动，尤其是扭转振动特性进行仿真研究，并通过对比实际测量数据对该仿真结果进行验证，以完善和充实推进轴系振动仿真的研究方法和理论。同时，通过对比船体变形前后的频响曲线，分析船体变形对轴系振动的影响。

1 刚柔耦合多体动力学理论

刚柔耦合多体动力学是指研究由若干个柔性和刚性物体相互连接组成并做着相对运动的复杂多体系统的运动规律的科学。它一般以多刚体系统动力学的研究为基础，对系统中对于需要考虑柔性影响的部件进行柔化处理，在机械系统中常用的处理方法有离散法、模态分析法、形函数法和有限单元等［9］。具体分析流程如图1所示。

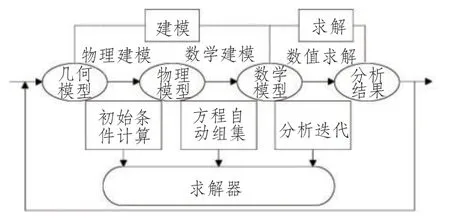
图1 多体动力学仿真技术分析流程Fig.1 The process of analysis based onmulti-body dynamics simulation technology

一般来说，对于需要考虑柔性影响的动力学问题，可根据三维弹性动力学基本方程及力的边界条件，并利用等效积分形式的Galerkin法，最终得到有限元格式下的动力学微分方程:

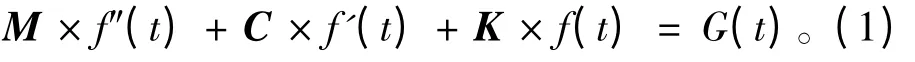
式中:M 为结构的质量矩阵;C 为结构的阻尼矩阵;K 为结构的刚度矩阵;f(t)为结构的节点位移量;G(t)为结构的节点载荷向量。

此方程为刚柔耦合多体动力学分析的基础公式。

2 刚柔耦合的大型船舶轴系仿真模型

以110 000 t 大型油轮为研究对象，所研究的船舶推进轴系主要包括传动轴(尾轴、推力轴和中间轴)、联轴节、中间轴承、推力轴承、尾轴管及螺旋桨等部分。

2.1 船舶推进轴系模型的建立

考虑到几何建模和仿真计算的简便，本文只对推进系统中对计算结果产生较大影响的各个部件进行建模，并对一些复杂的、无关紧要的结构进行简化，其中包括推进轴系的曲轴、1 根中间轴、1 根尾轴、联轴法兰、中间轴承、尾轴承及简化后的螺旋桨进行三维建模，如图2所示。各个零件的尺寸参数如表1所示。

图2 船舶推进轴系模型Fig.2 Model of ship propulsion shafting

表1 船舶推进轴系模型主要参数Tab.1 Main parameters of model of ship propulsion shafting

2.2 刚柔耦合模型的建立

通过有限元软件Ansys 对轴系与轴承进行柔化。其中轴系采用Solid45 单元属性定义，划分网格后，生成mnf 模态中性文件，导入Adams 替换相应的刚性零件。由于船舶推进轴系的各个部件之间具有一定的相对运动关系，因此为了将实际各部件之间的运动关系转化为Adams 中理想的运动副约束就要在各部件之间施加运动约束，通过约束来限制不必要的运动，从而形成一个完整的船舶推进轴系。生成的船舶推进轴系刚柔耦合模型如图3所示。

图3 船舶推进轴系刚柔耦合多体动力学模型Fig.3 Rigid-flexible coupling multi-body dynamics model of ship propulsion shafting

3 刚柔耦合模型多体动力学仿真分析

3.1 额定转速下船舶推进轴系扭转振动分析

在额定工作状态，即轴系转速为105 r/min，平均扭矩为1 298 181.2 N·m的条件下对上述刚柔耦合轴系模型进行多体动力学仿真及求解，得到轴系各主自由节点随轴系转动时的各方向位移量、各轴承受力、角速度、角加速度、轴心轨迹、轴系变形、转速波动等参数。图4所示为在3 s 时间内，轴系扭转角振动幅度变化量。

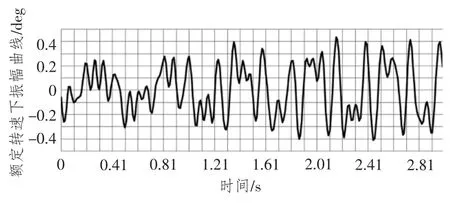
图4 轴系扭振的变化曲线Fig.4 Changing curve of shafting torsional vibration

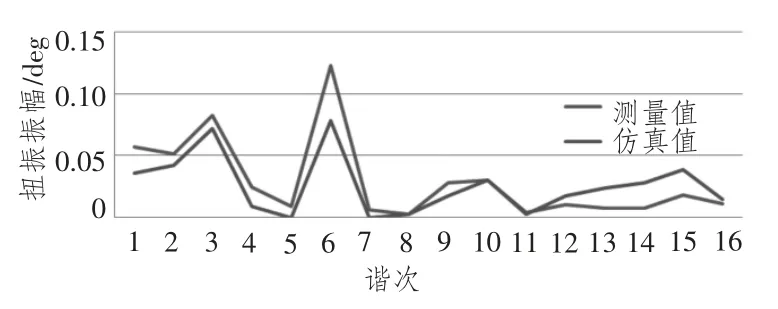
图5 轴系扭振振幅的谐次对比图Fig.5 Contrast comparison of shafting torsional vibration in different orders

对图4 中的时域振幅曲线进行傅立叶变换转化为谐次图。从图4 可看出，额定工况下，轴系扭转振动在2.16 s 时达到最大值，为0.44 deg;从图5 可看出，额定转速下，在3，6，10，15 谐次处可能会激起较大程度的轴系扭转振动，其中6谐次激起的振动最大，达到了0.078deg;3，6 谐次扭振幅值较大可能与其振动频率接近2 阶和4 阶系统固有频率有关。对比实际测量值和仿真计算值可以发现其变化趋势基本一致，只是在扭振幅值的大小上有一定的差别，10 谐次之前仿真值相对于测量值较小，10 谐次之后仿真值逐渐增长，大于相应谐次的测量值。造成扭振振幅不一致的原因可能在于输入端激励不足或者模型简化导致的转动惯量的减少。

3.2 多转速下船舶推进轴系扭转振动分析

通过在Adams 中修改相应的参数，可以对推进轴系在不同转速下的扭振情况进行分析，图6所示为在不同谐次下多转速轴系扭振仿真计算结果曲线。

从图6 可看出:3 谐次和6 谐次在全转速范围内都出现了最大或者次大的峰值，尤其是6 谐次在大部分转速下振动幅值远远大于其他谐次。在不同转速下扭转振动还有其各自特点，例如在较大转速下10 谐次出现很高峰值，30 r/min下9 谐次出现较高峰值等，这都是与轴系扭振固有频率吻合而造成的“合拍”现象。

图6 柴油机转速对船舶推进轴系各谐次扭振的影响Fig.6 Influence of rotate speed to torsional vibration of ship propulsion shafting in various orders

同时，从图6 可发现，在转速30～105 r/min的范围内，6，8，9，15 谐次在50 r/min下有较大的振幅峰值，其中6 谐次振幅最为明显，为0.11 deg;而3，10，14 谐次在100 r/min下扭振振幅有较大增长。

3.3 船舶推进轴系扭转振动仿真与试验对比分析

为验证仿真结果的正确性，利用船舶海试的机会在实船上测量航行时的扭振数据，将此船船舶推进轴系扭转振动有限元仿真计算结果与实船试验测试数据进行对比。

在实船上进行测试时，可以通过测试系统通道进行扭转振动信号的采集和分析，直接得到各个转速工况下和不同谐次下的扭振特性。将轴系振动仿真计算和测试系统得到数据进行对比，分别如图7和图8所示。取仿真计算中振幅较为明显的2个谐次进行对比，图7 为3 谐次下不同转速工况的扭振变化，图8 为6 谐次下不同转速工况的扭振变化。表1 为仿真计算结果和试验结果的对比。

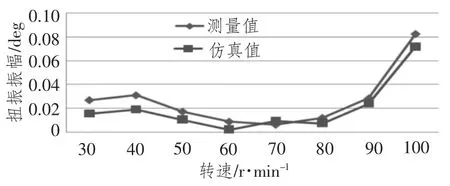
图7 在3 谐次下的轴系扭振对比Fig.7 Contrast of shafting torsional vibration in tired orders

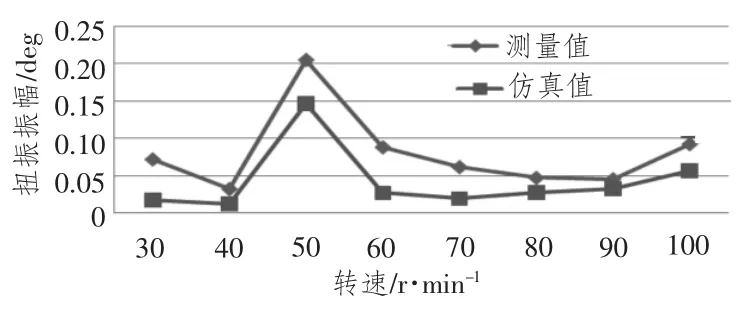
图8 在6 谐次下的轴系扭振对比Fig.8 Contrast of shafting torsional vibration in sixth orders

表2 仿真结果与实验结果对比Tab.2 Contrast of results between experiment and simulation

根据图7、图8 及表2的船舶推进轴系动力学仿真计算结果和试验测试结果对比可看出，在3谐次下，轴系扭振振幅最大值的仿真结果和试验结果相对误差为13.4%;在6 谐次下，轴系扭振振幅最大值的仿真结果和试验结果相对误差为28.7%。仿真计算得到的轴系扭转振幅变化规律与试验结果基本一致，只是幅值大小上有所差异。说明本文所建立的船舶推进轴系刚柔耦合多体动力学模型是合理的，所采用的多体动力学和有限元仿真方法比较好地反映了轴系的实际动态特性。而造成图中所示幅值差异的主要原因是建立的船舶推进轴系多体动力学仿真模型未考虑发动机输出扭矩激励的变化及飞轮等零部件的影响，这样与实船轴系扭振测量试验数据必然存在一定的差异。

4 船体变形对轴系扭转振动的影响

当船舶航速剧烈变化时，船体与波浪相互作用发生剧烈的动态变形，尤其对于大型油轮和散货船而言，其轴系较短，轴系刚性对船体变形极为敏感，在不同载重工况下，轴系中心线的相对变形较大，导致轴系轴承的相对位置、负荷发生剧烈变化，甚至超出保持轴系正常运转所允许的范围，由于船体主参数较大，推进轴系传递的扭矩、推力巨大，导致船舶轴系振动加剧［11］。但目前多数研究在建立船舶推进系统模型时都忽略了船体变形的影响［12］。

此刚柔耦合仿真模型是以110 000 t 油轮为研究对象，因此船体变形对推进轴系振动影响相对较大。为分析轴承位移对船舶推进扭转振动的影响，采用Adams/Vibration 模块，在螺旋桨中心设置振幅为1.298 ×106N·m，相位为0的激振力矩作为输入通道，同时在轴承位置施加105N的竖直向上的力，使轴承与轴产生y 方向的位移。在轴上一点设置轴系扭振的输出通道，随后对推进轴系进行强迫振动分析，设置扫频起点为0.1 Hz，终点为10 000 Hz，采样数1 000个，得到船舶推进轴系在船体变形的影响下的扭振频响曲线 (实线)，并与船体无变形的频响曲线 (虚线)对比，如图9所示。

图9 船体变形对船舶推进轴系扭振的影响Fig.9 Influence of ship hull deformation to torsional vibration of ship propulsion shafting

从图9 可看出，在船体发生变形后扭振振幅明显增大，尤其是在低频，即10 Hz 范围内，扭振振幅增大相当明显，其最大值从无变形时的23 dB 增长到有变形时的71 dB;而在高频范围100～1 000 Hz 中，船体变形对轴系扭振几乎没有影响。而从响应峰值的位置上看，施加船体变形后峰值位置向低频移动，由原来的1.4 Hz 降低到0.82 Hz。由此可知:船体变形对低频的扭振影响较大，能够大幅提高扭振振幅，而且会使响应峰值向地平移动;对于高频扭振则影响不大。

5 结 语

本文以110 000 t 油轮推进轴系为研究对象，应用多体动力学理论结合有限元理论对其扭振特性进行研究。应用有限单元法建立推进轴系刚柔耦合模型进行动力学仿真分析，讨论了不同转速和谐次下，船舶推进轴系扭转振动的变化规律，并与试验测量值进行了对比，验证模型的准确性。同时，通过Adams/Vibration 对船体变形对轴系扭振的响应进行了比较分析。通过总结，初步形成船舶推进轴系基于多体动力学和有限元仿真的扭振特性预估方法。

［1］周春良.船舶轴系振动研究［D］.哈尔滨:哈尔滨工程大学，2006.

［2］黎辉.船舶推进轴系扭振若干技术问题研究［D］.武汉:武汉理工大学，2007.

［3］于招阳.船舶轴系扭振特性与应力工程预报研究［D］.上海:上海交通大学，2011.

［4］LEONTOPOULOS C，DOVIES P，PARK K R.Shaft alignment analysis:solving the reverse problem［J］.Proceedings of the Institute of Marine Engineering，Science and Technology Part B:Journal of Marine Design and Operations，2005(8B):3－12.

［5］严济宽.机械振动隔离技术［M］.上海:上海科学技术文献出版社，1985.

［6］段秀兵.基于低噪声发动机虚拟设计的曲轴机体耦合动力学研究［D］.天津:天津大学，2004.

［7］赵鸿铎，梁颖慧.基于有限元分析的沥青路面自振频率研究［J］.交通信息与安全，2012，30(2):10－15.ZHAO Hong-duo，LIANG Ying-hui.Natural frequence of asphalt pavement via finite element analysis［J］.Transport Information and Safety，2012，30(2):10－15.

［8］马炳杰，周文建，童宗鹏，等.船舶传动装置多体动力学和有限元仿真技术［J］.舰船科学技术，2011，33(12):51－56.MA Bing-jie，ZHOU Wen-jian，TONG Zong-peng，et al.Multi-body system dynamics analysis and finite element simulation onmarine power transmission system［J］.Ship Science and Technology，2011，33(12):51－56.

［9］洪嘉振，刘铸永.刚柔耦合动力学的建模方法［J］.上海交通大学学报，2008，42(11):1922－1926.HONG Jia-zhen，LIU Zhu-yong.Modeling methods of rigidflexible coupling dynamics［J］.Journal of Shanghai Jiaotong University，2008，42(11):1922－1926.

［10］陈立平.机械系统动力学分析及ADAMS 应用教程［M］.北京:清华大学出版社，2005.

［11］严新平，李志雄，袁成清，等.考虑船体变形耦合作用的船舶推进系统建模与控制［J］.船海工程，2011，40(1):60－63.YAN Xin-ping，LI Zhi-xiong，YUAN Cheng-qing，et al.Modelling and control of marine propulsion system coupled with hull deformation［J］.Ship ＆ Ocean Engineering，2011，40(1):60－63.

［12］PAUL S.The Interaction between diesel engine，ship and propeller during manouevring［D］.Netherlands:Technische Universiteit Delft，2005.