抛光过程游离单颗磨粒与光学元件间滚动摩擦接触分析

陈为平， 高诚辉,2， 任志英,2， 林春生

(1. 福州大学机械工程及自动化学院，福建 福州 350108；2. 福州大学摩擦学研究所，福建 福州 350002；3. 福建福光数码科技有限公司，福建 福州 350015)

抛光过程游离单颗磨粒与光学元件间滚动摩擦接触分析

陈为平1， 高诚辉1,2， 任志英1,2， 林春生3

(1. 福州大学机械工程及自动化学院，福建 福州 350108；2. 福州大学摩擦学研究所，福建 福州 350002；3. 福建福光数码科技有限公司，福建 福州 350015)

针对游离单颗磨粒与光学元件滚动接触过程中摩擦、磨损机理分析的不足及如何有效控制滚动单颗磨粒对光学元件亚表面损伤的影响等问题，基于滚动接触理论，提出了一种具有分形特征表面的单颗磨粒与光学元件双粗糙面间的摩擦、磨损接触模型，并运用有限元仿真分析微观动态滚动的接触过程。通过对不同剪切强度下接触力、接触应力、磨粒角度及其对亚表面损伤的影响等分析，发现随着剪切强度的增强，磨粒与光学元件表面接触界面间的摩擦系数将减小，最佳的磨粒角度为 105°～120°，并且分形特征的单颗磨粒对亚表面损伤的影响要大于球形特征单颗磨粒，这说明了研究分形特征游离单颗磨粒滚动接触的必要性和重要性，为更加深刻了解滚动接触过程的摩擦机理提供了借鉴意义。

游离单颗磨粒；亚表面损伤；磨粒角度；滚动接触；有限元分析

随着光学玻璃在航空航天、能源、生物医药及光电子等领域得到广泛应用，对其表面质量要求越来越高。但因其是脆性材料，在加工中不可避免地会出现损伤或裂纹，而抛光技术作为光学元件加工中的最后一道工序，对提高元件加工质量及成品率等方面起着非常重要的作用。因此，作为先进制造技术重要组成部分的抛光加工技术越来越受到人们的广泛关注，其基本原理是：磨具在研抛液中高速旋转，并与工件表面相接触；工件固定在工作台上并随之一起旋摆。磨具的旋转运动与工件的旋摆运动的共同作用，保证了工件的材料去除及加工精度。而按照抛光中磨粒加工形式的不同可分为：固结磨粒抛光和游离磨粒抛光。两种形式能够改善工件表面加工精度和光学性能，可提高材料的表面均匀性及完整性，是保证产品加工精度和表面质量的重要方法[1-4]。

目前，磨粒加工中磨粒对材料去除机理的研究已取得了一定的成果，尤其是对固结磨粒的研究相对较成熟，但对于研磨接触过程中更加普遍存在的游离磨粒的研究相对较少。著名的 Preston方程对游离磨粒化学机械抛光(chemical mechanica polishing)进行研究，提出材料去除速率公式，认为去除速率与抛光压力和相对运动速度成正比，未涉及微观研究。文献[5-6]基于压痕断裂力学理论和孔洞扩张Hill模型，研究了尖锐磨粒印压下亚表面裂纹的深度分布，为亚表面损伤的理论研究奠定基础。基于脆性材料的压痕断裂理论，文献[7-9]对尖锐磨粒在K9玻璃研磨过程中产生亚表面损伤进行了研究分析，并提出亚表面损伤裂纹深度的预测模型。文献[10]研究了半固着磨粒加工工艺参数对材料去除效率和表面粗糙度的影响，并进行了加工实验，通过与游离磨粒加工的对比实验和理论分析，对半固着磨粒磨具的去除机理进行了研究。文献[11]利用游离和固结磨粒分别进行抛光，表明磨粒粒径在游离磨料抛光中的作用比固结磨料抛光显著，但仅从宏观的抛光后表面粗糙度进行了对比分析。文献[12]运用固液两相流理论，对磨粒流加工过程进行了数值模拟，为磨粒流加工过程中主要参数的选择提供了一些参考依据，但没有对单颗磨粒在加工中的摩擦磨损行为做进一步的研究。Malkin[13]基于实验研究，把滑动接触力、磨粒和工件间的摩擦系数、平均接触压力及接触面积进行联系，得出各参数间的相互关系，对于更加深入理解磨粒与粗糙面摩擦接触过程具有积极意义。文献[14-15]针对三体磨料磨损系统中球形特征单颗磨粒的受力情况，给出了三体运动接触中的滑动和滚动接触的判定，如图1所示。

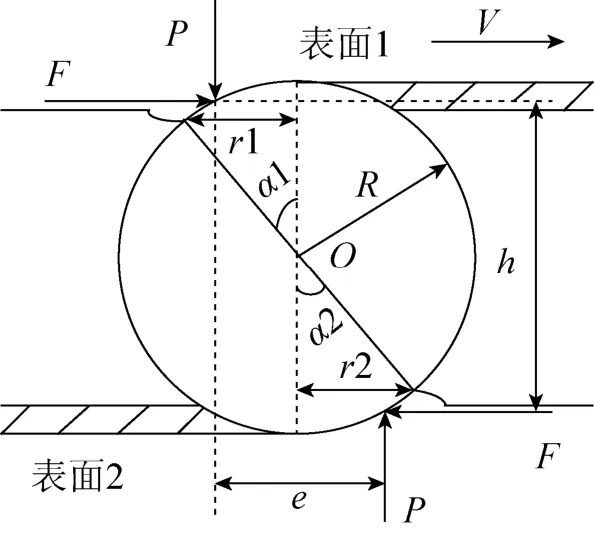
图1 摩擦界面球形磨粒受力分析

其中，e和h分别为正向压力P和水平剪力F的力臂；r1和r2分别是单颗磨粒与表面1和表面2接触点到中心线的距离；α1和α2分别是表面1和表面2接触点与中心线间的夹角；R是单颗磨粒的半径；V是单颗磨粒的运动速度；μs和μr分别为滑动摩擦系数和滚动摩擦系数；μk是单颗磨粒相对于材料表面滑动，并引起表面屈服时的摩擦系数。

游离磨粒在研磨过程中无需考虑磨粒的磨损，但在研究过程中仍存在许多困难，如：磨粒流难以控制，研抛加工量不均匀；加工效率低、条件不稳定等。现有研究主要集中在宏观层面，微观层面的研究仍缺乏对单颗磨粒与工件冲击接触瞬间的材料去除机理及其对材料亚表面损伤的研究，且把磨粒视为理想的球形，而忽略了球形特征磨粒表面的粗糙情况及磨粒角度，与实际情况不相符。

因此，本文针对研磨中游离磨粒与光学元件间的冲击接触过程，利用有限元软件建立了具有分形特征的游离单颗磨粒与光学元件间双粗糙面的滚动接触模型，仿真分析了在不同牵引力和不同磨粒微凸体角度下接触过程中的力学、应力场问题，从而对接触过程中的摩擦机理及对光学元件亚表面损伤影响进行分析。

1 分形表面磨粒与粗糙表面的接触模型建立

1.1 摩擦接触模型的建立

鉴于实际中许多工程表面通常具有分形特征，本文采用连续并且具有自仿射分形特性的(Weierstrass-Mandelbrot，W-M)分形函数[11-12]来模拟粗糙光学表面和磨粒表面，为了更为直观地观测到摩擦接触过程中应力及亚表面损伤的实时变化情况，采用了二维接触模型。图2显示的是具有分形特征的粗糙表面和单颗磨粒的网格划分模型。

如图2(a)所示，A、B、C、D分别为分形粗糙表面的4个顶点，通常亚表面损伤深度分布在距离表面约0～100 μm范围内，为了能够更好地反映出摩擦接触过程中应力的变化，本文建立粗糙表面深度AC为300 μm；同时为了使接触结果更具有普遍性和有效性，粗糙表面长度AB为1 270 μm，能够满足磨粒在其表面作5个完整周期的滚动。图2(b)具有分形特征单颗磨粒金刚石的硬度比光学元件大很多，同时为了简化模型，在摩擦接触过程中将其视为刚体。

图2 具有分形特性的粗糙表面和单颗磨粒网格划分模型

针对研磨中游离磨粒与光学元件间的冲击接触过程，利用有限元软件建立了分形特征游离单颗磨粒与光学元件间双粗糙面的滚动接触模型，仿真分析了在牵引力分别为10 000 μN、8 000 μN、6 000 μN、4 000 μN及不同磨粒微凸体角度(5组)下接触过程中的力学、应力场问题，从而对接触过程中的摩擦机理及其对光学元件亚表面损伤影响进行分析。选用常见的金刚石磨粒和K9玻璃作为实验材料[7-8]。磨粒材料属性如表1所示。

表1 磨粒材料属性

本文所建立的分形特征游离单颗磨粒与粗糙表面间的微观动态滚动接触模型如图3(a)所示；作为对比，建立了理想球形单颗磨粒与粗糙表面间的滚动接触局部模型，如图3(b)所示。为进一步研究游离单颗磨粒与粗糙光学元件表面间滚动接触过程中磨粒角度对亚表面损伤的影响，在图3(a)中选取了5个接触频率最高的微凸体进行分析，其角度参数如表2所示。

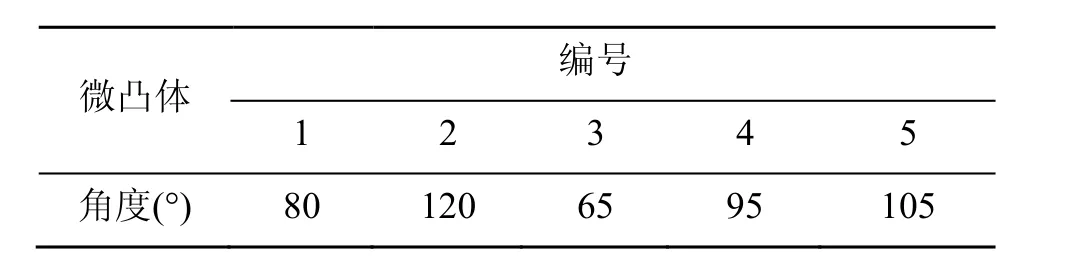
表2 磨粒接触过程微凸体角度

1.2 破损机理的选择

材料在摩擦接触过程中产生破坏，准确又有效地反映仿真过程中材料的破坏情况是仿真的关键问题。目前，在材料的破坏准则方面主要是利用四大强度准则理论来进行相关的破坏判定。

其中，最大拉应力是引起材料脆性断裂破坏的主要原因，无论应力处于何种状态，只要材料内一点处3个主应力中的最大拉应力σ1达到单向应力状态下材料的极限应力值σb，则会导致材料发生脆性断裂。

在ABAQUS软件模拟动态仿真方面，本文选择更适合脆性裂纹萌生扩展的ABAQUS/Explicit中脆性破裂模型concrete brittle cracking model。

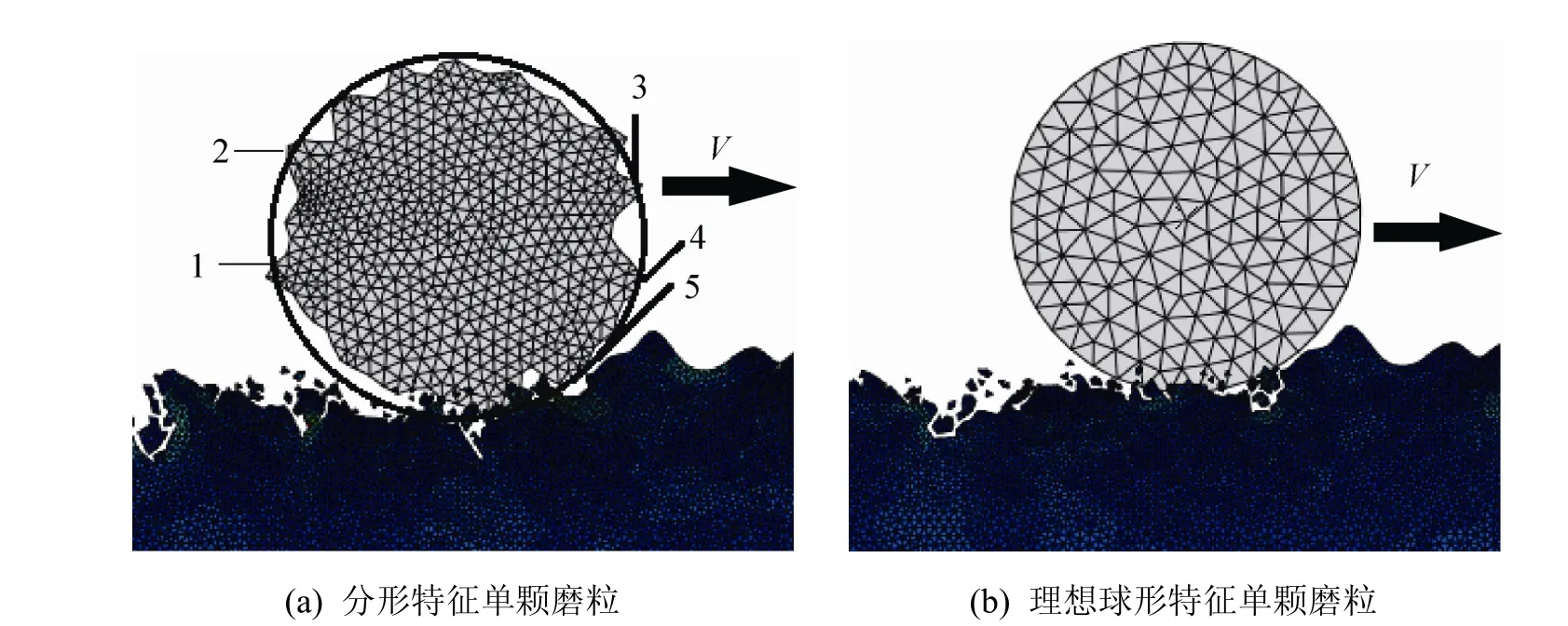
图3 分形与理想球形特征单颗磨粒与粗糙表面接触过程局部模型

1.3 力学建模与分析

考虑到游离单颗磨粒的表面真实性，采用了具有分形特征粗糙表面，同时由于磨粒粗糙表面的微凸体具有圆锥体的一般形式，则视假设磨粒的分形表面圆形微凸体为圆锥体，则具有分形特征的磨粒表面微凸体与粗糙表面接触过程中的受力分析如图4所示[16]。

图4 游离单颗磨粒微凸体滚动接触过程受力分析

通过假设磨料是具有刚性的圆锥形。塑性变形区和径向裂纹是由于加载磨粒时产生的高应力而形成的，横向裂缝是由于卸载期间产生的残余应力导致的。其中，圆锥形磨粒的锐度角(半角)为θ，工件的屈服应力为σy，与工件的屈服强度有关，是个常数。当磨粒在法向力N和切向力Ft的作用下接触到工件表面，磨粒将开始滚动并印压工件表面。如图4所示，在磨粒与工件接触区域内用于平衡磨粒受力的外部载荷有法向力Fn和摩擦力(Fl和Fm)。假设所受载荷Fn、Fl、Fm的合力沿着磨粒的锥形边。其中磨粒的法向力是由于研磨液的流体动压等导致的，而切向力是在滚压过程中快速运动产生的。则可以推导得出：

其中，外部载荷Fn、Fl、Fm可表示为：

式中，Fn、Ft分别为磨粒微凸体的切向力和法向力(N)，μ为磨粒与元件间的摩擦系数，θ为磨粒的半顶角(rad)，σ为元件的屈服应力(N/mm2)，ai为其塑性变形区的半径(mm)，A是磨粒与基体间的接触面积。

将式(3)和式(4)代入式(1)，可得：

整理得：

将式(3)、式(4)和式(5)代入式(2)，可得：

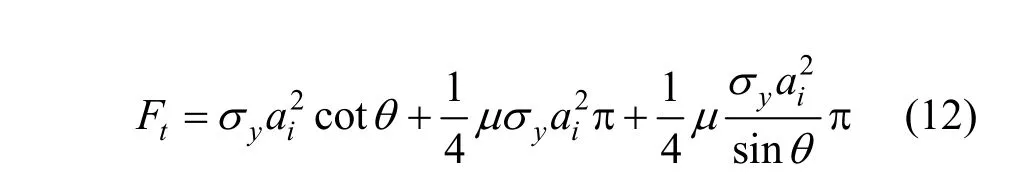
整理得：

则，式(9)、(13)分别为施加到磨粒上的法向作用力和切向作用力。

2 仿真结果分析

2.1 接触过程中力的分析

研磨过程中的接触力可分为切向力和法向力。切向力和法向力在磨粒与粗糙表面接触过程中将产生不同的力矩，且力矩间的平衡关系决定了磨粒与粗糙表面间的运动关系是滑动还是滚动。因此，对不同牵引力作用下具有分形特征游离单颗磨粒微观滚动接触过程进行了分析。分形特征的磨粒滚动接触过程中切向力的变化趋势如图5所示，法向力的变化趋势如图6所示。

图5 不同牵引力下，分形特征的磨粒滚动接触过程切向力变化趋势

从图5和图6中可以看出刚开始接触时，基体由处于平衡状态到接触瞬间的应力集中，而后陆续又有接触切应力，且后半部分接触时产生的切应力要比前半部分大，同时密集度也高，说明后半部分表面的粗糙程度较大；且随着牵引力的增大，切向力和法向力皆呈现出一定的递减趋势。

在接触过程中出现了切向力和法向力间幅值为零的间隔部分，这可能是由于磨粒是具有分形特征的微观粒子，光学元件表面也具有分形粗糙度，所以在磨粒与工件双粗糙表面滚动接触过程中，难免会出现某一瞬间接触不到的情况；且在有限元软件ABAQUS中接触对的定义为磨粒表面与光学元件粗糙表面间的接触，当磨粒与粗糙面接触时由于应力作用使完整未损伤的表面也发生一定程度的破损，从而破坏了接触对，导致没有接触力的显示。从图中可以看出前半部分间隔较大，而在时间为0.004 s左右时接触力间没有间隔，这再次说明了后半部分的粗糙度较大，与模型粗糙度分布相符。

图6 不同牵引力下，分形特征的磨粒滚动接触过程法向力变化趋势

从整体上看，接触过程中的切向力和法向力之间在位置上存在一一对应关系，对于不同的剪切强度，接触力也不同，且显示的接触力随着剪切强度的增大而增多，这是因为剪切强度增大导致的材料破损程度也增大。不同剪切强度下，各接触力间的关系如表3所示。

表3 不同剪切强度下，法向力与切向力间的关系

从表3可以看出，不同剪切强度下，平均法向力值要明显大于平均切向力值；平均法向力与平均切向力的小大随牵引力的增大而递减，且减小幅度变小。在摩擦过程中，摩擦系数可认为是平均切向力与平均法向力之比，则在滚动摩擦接触过程中，随着剪切强度的增大，摩擦系数呈现递减趋势。

2.2 接触过程中应力的分析

磨粒在与光学元件表面研磨过程中将在接触点处产生应力，并迅速影响基体，本仿真选取了3种主要应力作为研究对象：等效应力(mises stress)、剪切应力(tresca stress)和最大主应力(max principal stress)。同时本文沿深度方向设置了一条有20个节点的路径，在不同剪切强度作用下，使分形特征游离单颗磨粒与光学元件表面相接触。

图 7(a)～(d)为不同牵引力作用下，分形特征游离单颗磨粒与粗糙表面接触时该路径的应力变化及亚表面损伤情况。图 8(a)～(d)分别为在牵引力为4 000 μN、6 000 μN、8 000 μN、10 000 μN下，等

效应力、剪切应力及最大主应力随亚表面损伤深度的变化趋势。从图8中可以看出，等效应力与剪切应力与亚表面深度间的变化趋势基本一致，而最大主应力随亚表面深度的变化却有所不同。各应力最大值的亚表面深度分布随剪切强度的增大而增大，即应力扩散速度随剪切强度的增大而增大，且最大主应力的亚表面深度均比对应的等效应力与剪切应力的亚表面深度小；当牵引力小于8 000 μN时，最大主应力大于其他应力，当牵引力大于8 000 μN时，最大主应力小于其他应力。应力存在波动是由于其他时刻接触时所产生的残余应力间的相互影响，图8(c)中应力在300 μm左右出现波峰，说明在基体底部出现了应力集中，即应力具有“反弹”现象。

图7 牵引力不同时，分形特征游离单颗磨粒与粗糙面接触路径分布

为了能够更好地说明游离单颗磨粒与粗糙表面接触过程中，各应力的变化反映在亚表面损伤深度及材料体积去除率上的情况，文中在磨粒粒径、速度、牵引力等加工条件保持不变的情况下，对不同形状游离单颗磨粒与粗糙面接触的滑动过程与滚动过程进行了相对应的比较，结果如图9和10所示。

从图9中可以看出，游离单颗磨粒与粗糙表面间的滚动接触过程导致的亚表面损伤要明显大于同等条件下滑动接触过程，这说明了进行滚动接触研究的必要性；同时，相同条件下分形特征的游离单颗磨粒与粗糙表面间滚动接触导致的亚表面损伤要明显大于球形特征的游离单颗磨粒滚动接触过程，而分形特征的游离单颗磨粒与粗糙表面间滑动接触导致的亚表面损伤要略小于球形特征的游离单颗磨粒滑动接触过程，这是因为分形特征的单颗磨粒在滑动过程中的接触角没有发生改变，即相当于一个更小的球形特征的单颗磨粒与粗糙表面滑动接触，所以导致的亚表面损伤也更小。从图10

中可以看出，滚动接触过程的体积去除率要明显大于滑动过程；同时滑动过程中，分形特征的磨粒与球形特征的磨粒产生的体积去除率几乎一致，但滚动过程中，分形特征的磨粒滚动接触过程产生的体积去除率要远大于球形特征的磨粒产生的体积去除率，这是因为分形特征的磨粒表面存在众多各不相同的微凸体，当磨粒滚动接触时，会以不同的接触角冲击粗糙表面，从而提高体积去除率。

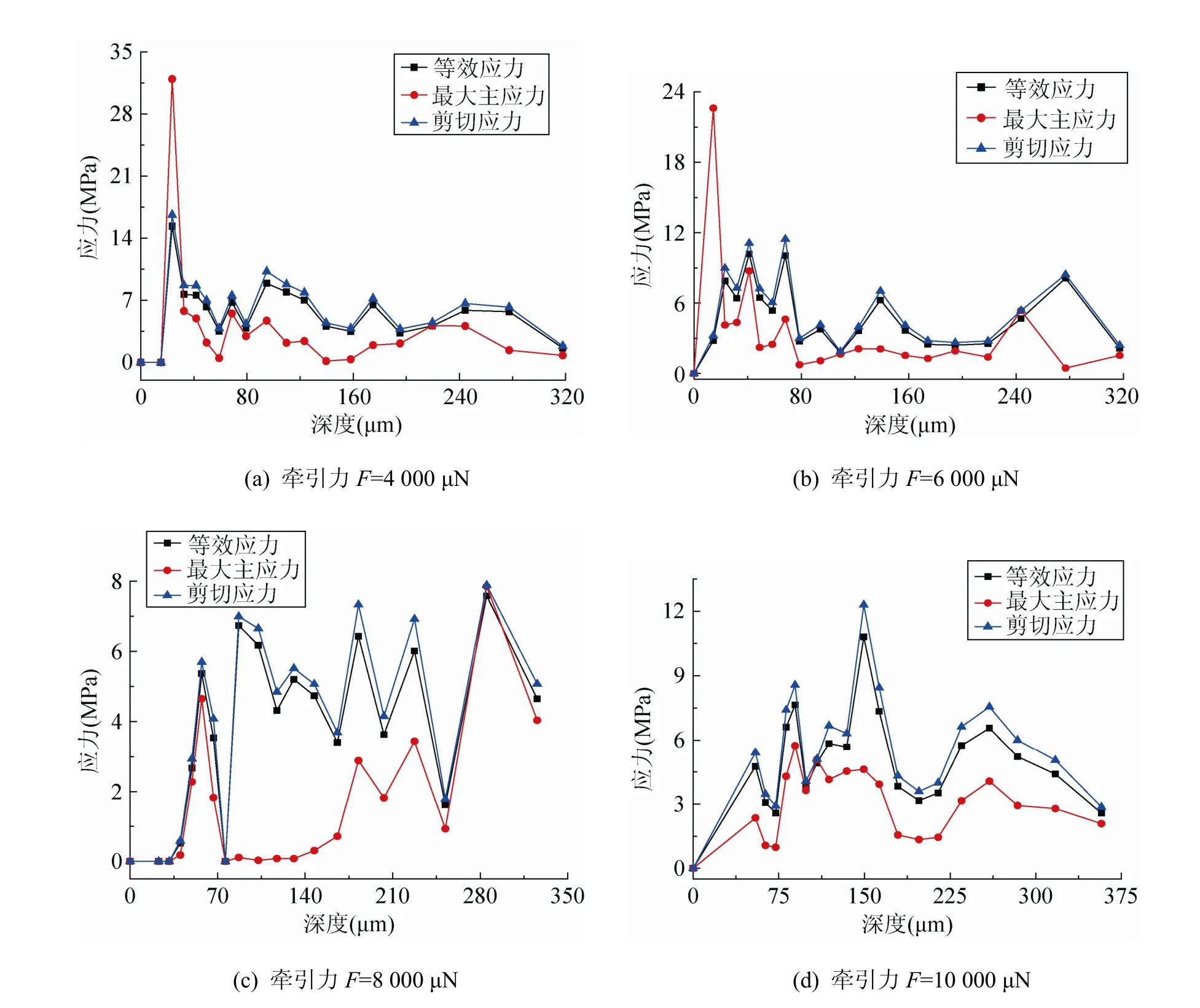
图8 分形特征游离单颗磨粒在不同牵引力下，应力随亚表面深度的变化

图9 磨粒与粗糙表面接触过程中亚表面损伤曲线

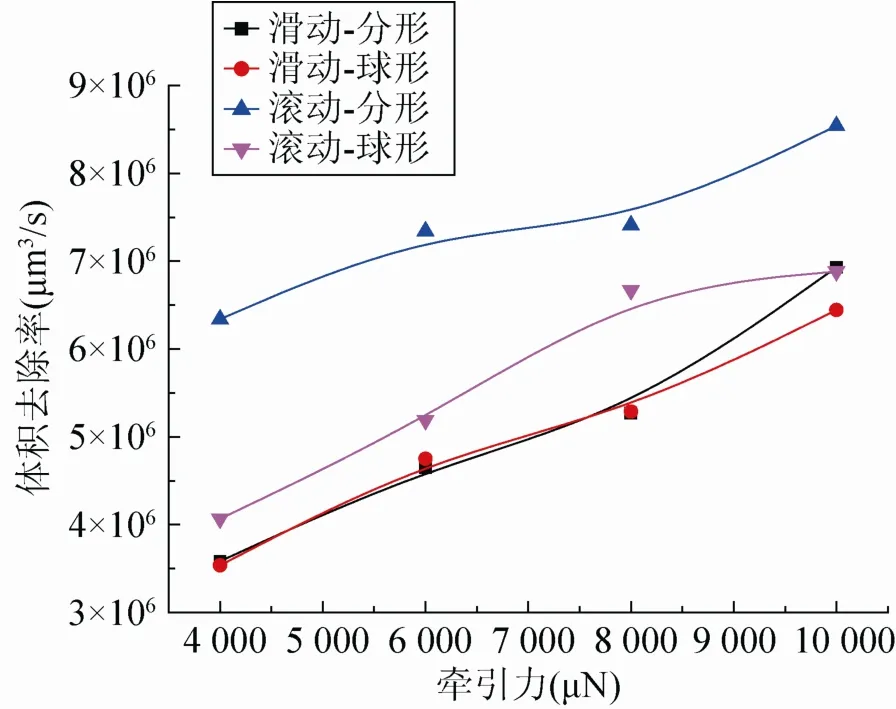
图10 磨粒与粗糙表面接触过程中体积去除率曲线

2.3 接触过程中磨粒角度分析

在游离单颗磨粒与光学元件滚动接触过程中，分形特征的磨粒上存在众多各不相同的微凸体。文中选取了5个接触最为频繁的磨粒角度进行分析，

各个角度在与光学元件表面滚动接触过程中所导致的平均亚表面损伤深度见表4。

表4 磨粒锐度角导致的平均亚表面损伤深度

从表4中可以看出，元件平均亚表面损伤深度随磨粒角度的增大而呈递减趋势；其中，当磨粒锐度角在 105°～120°之间时，导致的平均亚表面损伤深度要明显小于其他角度，利于加工。

3 结 论

针对光学镜片加工，建立了更符合实际情况的磨粒与光学分形表面间的滚动摩擦接触模型，而不是滑动接触，充分考虑微观颗粒的实际表面形貌特征，建立了具有分形特征的磨粒，而不是简化为圆形或锥形，通过实例仿真，得出以下结论：

(1) 通过对比，滚动接触导致的亚表面损伤与体积去除率要大于滑动接触；分形特征的磨粒导致的亚表面损伤及体积去除率都要大于球形特征的磨粒，说明了研究分形特征的磨粒滚动微观接触的必要性和重要性。

(2) 随着剪切强度的增强，磨粒与光学表面接触界面间的摩擦系数将减小，可以利用提高剪切强度来减低研磨过程中的摩擦阻力，从而提高加工效率和加工质量。

(3) 分形特征的单颗磨粒微凸体的锐度角对亚表面损伤深度有影响，亚表面损伤深度将随微凸体的锐度角的增大而减小，本文中最优的研磨角度为105°～120°。

[1] 李长河, 侯亚丽, 蔡光起, 等. 游离磨粒精密光整加工方法综述[J]. 精密制造与自动化, 2009, (1)： 4-9.

[2] 李长河, 侯亚丽, 蔡光起, 等. 游离磨粒精密光整加工方法综述(续)[J]. 精密制造与自动化, 2009, (2)： 10-15.

[3] 计时鸣, 唐 波, 谭大鹏, 等. 结构化表面软性磨粒流精密光整加工方法及其磨粒流动力学数值分析[J]. 机械工程学报, 2010, 46(15)： 178-184.

[4] 楚文斌, 林大钧, 陈 浩，等. 刀具参数对加工表面粗糙度影响的研究[J]. 图学学报, 2014, 35(1)： 52-56.

[5] Lambropoulos J C, Jacobs S D, Gillman B E, et al. Deterministic microgrinding, lapping, and polishing of glass-ceramics [J]. Journal of the American Ceramic Society, 2005, 88(5)： 1127-1132.

[6] Weyl W A. Structure of subsurface layers and their role in glass technology [J]. Journal of Non-Crystalline Solids, 1975, 19： 1-25.

[7] 李圣怡, 王 卓, 吴宇列, 等. 基于研磨加工参数的亚表面损伤预测理论和试验研究[J]. 机械工程学报, 2009, 45(2)： 192-198.

[8] 王 卓, 吴宇列, 戴一帆, 等. 研磨加工中光学材料亚表面损伤的表征方法[J]. 纳米技术与精密工程, 2008, 6(5)： 349-355.

[9] 吕东喜, 王洪祥, 黄燕华. 光学材料磨削的亚表面损伤预测[J]. 光学精密工程, 2013, 21(3)： 680-686.

[10] 华钱锋. 基于半固着磨粒磨具加工的材料去除机理研究[D]. 杭州： 浙江工业大学, 2009.

[11] 王 军, 李 军, 朱永伟, 等. 游离和固结金刚石磨料抛光手机面板玻璃的试验研究[J]. 金刚石与磨料磨具工程, 2009, (2)： 13-17.

[12] 李 艺. 游离磨粒加工中流场的数值模拟与实验研究[D]. 湘潭： 湘潭大学, 2007.

[13] Malkin S. Grinding technology： theory and applications of machining with abrasives [M]. Chichester： Ellis Horwood, 1989： 115-157.

[14] 杜道山, 方 亮, 李从心. 三体磨料塑变磨损中磨粒运动方式的研究[J]. 润滑与密封, 2004, (6)： 66-68.

[15] Johnson K L. Contact mechanics [M]. Cambridge：Cambridge University Press, 1987： 242-284.

[16] Yang Fuqian, Kao I. Free abrasive machining in slicing brittle materials with wiresaw [J]. Journal of Electronic Packaging, 2001, 123(3)： 254-259.

Analysis of Rolling Friction Contact between Free Single Abrasive and Optical Element

Chen Weiping1, Gao Chenghui1,2, Ren Zhiying1,2, Lin Chunsheng3
(1. School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou Fujian 350108, China; 2. Tribology Institute of Fuzhou University, Fuzhou Fujian 350002, China; 3. Fujian Forecam Optical Technology Co., Ltd, Fuzhou Fujian 350015, China)

In order to study the deficiency of the friction and wear mechanism analysis and how to effectively control the impact of the subsurface damage during the process of rolling contact between free abrasive and optical element. Based on the rolling contact theory, a rolling contact model of dual fractal surfaces is established between single free abrasive and optical element, and the simulation of the microscopic dynamic rolling contact process is achieved by the use of the FEM simulative analysis. Through the analysis of the contact force, contact stress, abrasive angles and related stress fields under different shear strength, showed that, with the shear strength increased, the friction coefficient of the contact interface between the grain and optical surface will be decreased, the best grinding abrasive angle is 105°–120°, the influence of the fractal abrasives on subsurface damage is greater than the spherical grains, the necessity and importance of the research about the free fractal

free single abrasive; subsurface damage; abrasive angles; rolling contact; finite element analysis

TH 161.14

A

2095-302X(2015)04-0537-09

2014-12-29；定稿日期：2015-02-05

国家自然科学基金资助项目(51175085)；清华大学摩擦学国家重点实验室开放基金资助项目(SKLTKF13B02)；福建省教育厅A类资助项目(JA13059)；福州市科技局资助项目(2014-G-74)；福建省自然科学基金资助项目(2015J01195)

陈为平(1989–)，男，福建莆田人，硕士研究生。主要研究方向为摩擦学研究、数字化设计等。E-mail：wpingchen@sina.cn

高诚辉(1953–)，男，福建福清人，教授，博士，博士生导师。主要研究方向为摩擦学研究、数字化设计等。E-mail：gch@fzu.edu.cn

abrasive in rolling contact is indicated, and a certain significance for deeper understanding of the friction mechanism during the contact process is provided.