基于改进最低水平线方法与遗传算法的矩形件排样优化算法
刘海明, 周 炯, 吴忻生, 罗家祥
(华南理工大学自动化科学与工程学院,广东 广州 510641)
基于改进最低水平线方法与遗传算法的矩形件排样优化算法
刘海明, 周 炯, 吴忻生, 罗家祥
(华南理工大学自动化科学与工程学院,广东 广州 510641)
传统的最低水平线方法用于矩形件排样时可能产生较多未被利用的空白区域,造成不必要的材料浪费。针对此缺陷,在搜索过程中引入启发式判断,实现空白区域的填充处理,提高板材利用率。在应用遗传算法优化矩形件排样顺序时,在进化过程中采用分阶段设置遗传算子的方法,改善算法的搜索性能与效果。通过改进最低水平线方法与基于分阶段遗传算子的遗传算法相结合,共同求解矩形件排样问题。排样测试数据表明,所提出的矩形件排样优化算法能够有效改善排样效果,提高材料利用率。
矩形件排样;优化算法;最低水平线;遗传算法
矩形件排样问题属于二维排样问题中的一类特殊优化问题,是指将一组给定尺寸的矩形零件在矩形板材上按一定方式进行排放,要求零件的排放不得超出板材边界,零件之间互不重叠,同时使板材利用率最大化。矩形件排样优化问题普遍存在于钣金、纸品、玻璃、家具等现代制造、加工行业中。从数学计算复杂性来看,该问题属于NP-Complete组合优化问题,很难在一个合理时间内获得问题最优解。因此,研究和设计有效的矩形件排样优化算法,具有重要的理论研究意义和应用价值。
自20世纪90年代以来,国内外许多学者针对矩形件排样问题作了研究,提出了不同的求解方法。多数文献将矩形件排样问题分为:矩形件的排放策略问题与矩形件的排放顺序问题考虑。前者指矩形件被排入板材时的靠排方式;后者指各个矩形件的排放顺序。对于矩形件排放策略,目前多采用基于启发式规则的方法。Jakobs[1]提出基于BL规则的排放策略,以优先向下、向左靠排的方式排放零件。刘德全和藤弘飞[2]在 BL策略基础上提出一种下台阶方法,在向左靠排的过程中也同时考虑向下靠排。Hopper和Turton[3]也提出了一种BL改进策略,考虑了排放过程中产生的孔洞的填充利用。Yeung和Tang[4]与Wei等[5]提出了一种基于最低水平线的排放策略,优先在具有最低高度的水平轮廓线上排放零件。Christoforos和Fleszar[6]提出一种剩余矩形匹配算法,将板材可用区域不断划分为矩形块并逐个排入矩形零件,以尽可能减少板材浪费。对于矩形件排放顺序问题,其本质为序列的组合优化问题。早期主要采用经验性做法处理,例如按矩形件高度、面积排序等标准确定矩形件的排放顺序。但这种相对硬性的处理方法,在用于不同排样实例时结果往往时好时差,适用性不强。此外,该方法仅能产生少量特定的解序列,对于排样问题往往难以得到最优解甚至次优解。目前,多采用一些基于进化思想的大规模搜索算法对矩形件排样顺序进行寻优,如遗传算法(genetic algorithm,GA)[7]、模拟退火算法[8]等。
本文对原有的最低水平线排放策略作了改进,考虑了板材空白区域的有效利用,避免材料浪费;在应用GA实现矩形件排样顺序优化时,针对GA可能出现的过早收敛、搜索效率低等不足,对传统GA进行算法搜索性能改进。改进的最低水平线方法与GA相结合,共同求解矩形件排样优化问题。
1 问题描述与数学模型
根据不同的实际应用与工艺要求,矩形件排样问题可有不同的表述。该问题的一般化描述为:给定已知矩形件的一组尺寸,在一个宽度确定、高度不限的矩形板材上不重叠地排入这些矩形件,并使得板材利用率最高。根据问题描述可知,排样过程应满足以下3个条件:①任何一个矩形件不能超出板材边界;②各矩形件不能出现重叠;③矩形件可以旋转,但矩形件的边需与板材边界平行,即矩形件只能以0°或90°排放。图1所示为一个包含8个矩形零件的排样实例,其中,阴影部分为不能利用的板材(常称为孔洞)。

图1 矩形件排样实例
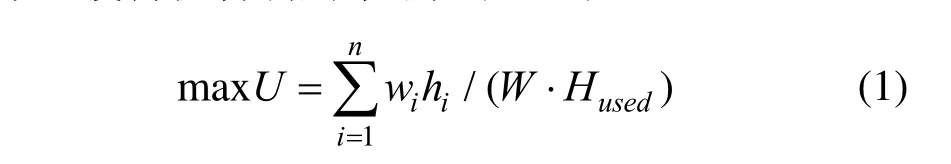
且满足约束条件:

其中,式(2)保证所有矩形排放时不超出板材边界,式(3)保证所有矩形之间不出现重叠。
2 基于改进最低水平线方法的排放策略
传统的最低水平线方法只考虑在高度最低的水平轮廓线上排放零件,但排放过程中并不考虑零件尺寸对排放布局的影响,在某些情形下会使板材出现较多孔洞而导致不必要的浪费。针对这一不足,本文提出了改进方法:在排放过程中,考虑待排放矩形件的尺寸,通过引入启发式判断条件灵活选择待排放矩形件,以充分利用板材可用区域。改进后的最低水平线方法的算法步骤如下:
步骤 1. 初始化板材的水平轮廓线集合,其仅包含一条水平轮廓线,即板材的底部边界,且为集合中的最低水平线;同时,设置变量i=1。
步骤2. 在给定的矩形件序列中,对第i个待排放矩形件pi,在当前水平轮廓线集合中找到当前高度最低的水平线(最低水平线),判断该水平线的宽度是否足够排入矩形件pi。如果可以排入,在该水平线上靠左排放该矩形件,并转入步骤4;否则,跳转到下一步。
步骤3. 对矩形件序列中pi后的所有未排放矩形件,判断其宽度大小是否可以在当前最低水平线上排放。对于能够排入的矩形件,优先选取宽度与最低水平线宽度相同的矩形件进行排放(若存在多个满足条件的矩形件,则选取高度最高的矩形件),然后交换该矩形件与矩形件pi在矩形件序列中的位置(即交换两者排放顺序),并转入下一步处理。若未能在当前最低水平线上找到可以排放的矩形件,则将当前最低水平线的高度提升至与其相邻且高度最接近的水平轮廓线,合并两段水平线。更新板材的水平轮廓线集合,然后跳转到步骤2继续处理。
步骤 4. 根据新排放的矩形件的位置及尺寸,更新板材的水平轮廓线集合。
步骤5. 若序列中尚有矩形件未排放,令i=i+1,转入步骤2继续处理;若所有矩形件已完成排放,则结束算法,此时板材的用量由水平轮廓线集合中高度最大的水平线决定。
在改进最低水平线方法中,通过启发式规则调整矩形件的排放顺序,使得板材空闲区域的利用更为灵活。算法中不仅考虑了小尺寸矩形件的填充排放,而且还考虑了宽度相同但高度不同的矩形件的排放顺序优化,优先排放高度较大的矩形件。因为高度较大的矩形件对板材用量的影响较大,优先排入高度较大的矩形件,可避免排样后期这些矩形件排放造成的材料浪费。改进最低水平线方法的算法流程如图2所示。

图2 改进最低水平线方法
图3和图4分别为针对同一排样算例(包含7个矩形件)按最低水平线方法和改进最低水平线方法排放的结果,其中矩形件初始排样序列为(1,2,3,4,5,6,7)。从排放结果可以看出,改进后的最低水平线方法能够更好地利用板材空间,使得板材利用率得到提高。

图3 基于最低水平线方法的排放策略

图4 基于改进最低水平 线方法的排放策略
3 基于改进遗传算法的矩形件排样优化算法
3.1 可行解的编码方式
从矩形件排样问题的特点可知,矩形件排样结果与矩形件的排样顺序密切相关。矩形件排样顺序的优化属于基于序列的组合优化问题,相对于局部搜索算法,具有全局搜索特性的GA能够获得更好求解结果。
所谓可行解编码,是指将排样问题的可行解从解空间转换为GA能够处理的搜索空间的解。常用编码方式有整数编码、实数编码和符号编码等。此处,基于排样问题特点,对排样可行解采用直观的十进制编码方式:对矩形件从1开始顺序编号,所有矩形件的编号所构成的序列就可以代表一个可行解(各编号所对应的矩形件在序列中的次序代表其排样顺序)。因此,对于包含n个矩形件的排样问题,其可行解集合为此外,为了在可行解中体现出矩形件是否旋转后排放这一信息,对上述编码方式进行扩展:为每个矩形件编号增加一个符号标志,若符号为正,表示矩形件排放时不旋转(按0°排放);若符号为负,表示矩形件旋转90°后再排放。
3.2 适应度函数
在GA中,需要建立一个适应度函数来评估可行解的优劣。对于矩形件排样问题,为使适应度函数能够反映解的优劣,选择如下适应度函数:

其中,Si为某个排样序列,AT为所有矩形件的面积之和,W为板材宽度,Hused(Si)为排样序列Si基于特定排样策略下的排样结果中矩形件水平轮廓线中最高水平线的高度。这样,适应度函数f (Si)的值就代表排样序列Si对应的板材利用率。易知,适应度函数的取值范围为(0, 1]。适应度函数值越高,表示对应的可行解(排样序列)越优。
3.3 遗传算法的改进处理
GA是一种具有全局寻优能力的进化算法,适合大规模组合优化问题的求解。但传统GA也存在一些缺点,例如过早收敛、搜索效率低等。本文从两方面对传统GA进行改进:首先,根据适应度的不同对父代解采取不同的进化操作,保证种群多样性,以避免种群过早收敛;其次,根据解的进化阶段动态调整遗传算子,提高算法自适应能力,使搜索能够更快逼近问题最优解。
(1) 选择、交叉和变异操作。为保证种群的多样性,根据可行解适应度的不同采取相应的进化处理。基本思路为:通过选择操作保留一部分适应度较好的父代解到子代种群中,通过对父代解的交叉、变异操作生成新的解补充到子代种群中;选择、交叉和变异操作所产生的解共同构成子代种群。
设种群大小为N,且进化过程中每一代种群大小不变,算法中的选择、交叉和变异操作如下所述:
①选择操作:又称复制操作,目的是把父代种群中具有较优适应度的解直接复制到子代种群中,保证良好基因的存在。方法是:预设一个选择算子ps(0 ②交叉操作:是在进化过程中产生新解的主要方法,可以改善种群的多样性。本文采用如下交叉方法:在余下的父代解(未被选择保留的父代解)中随机选中两个解,采用两点交叉方法产生两个新的可行解进入下一代。关于两点交叉方法,已有较多文献介绍,此处不再赘述。每两个随机选取的父代解都可以通过两点交叉方法获得两个新解。交叉操作产生的新解数量为pcN,其中N为种群大小,pc为预设的选择算子(0 ③变异操作:是一种产生新解的方式,是交叉操作的有益补充。根据排样问题的特点,本文采用两种变异操作:交换变异与旋转变异。交换变异对随机选中的某个父代解中的两个随机位置上的基因进行位置交换,从而得到一个新的排样序列(可行解)。旋转变异用于调整矩形件排放时的排放角度,其操作方法是:对于随机选中的某个父代解,在区间[1, n]之间产生一个随机位置(n为排样序列长度),将该位置对应的矩形件编号的符号取反(意味着改变矩形件的排放角度),从而得到一个新解。 每个被随机选中的父代解都可以通过交换变异或旋转变异操作得到一个新解。两种变异操作产生的新解数量分别由预设的交换变异算子 pme(0 需要说明的是,为了保持每代的种群大小不变,各算子的取值应满足条件:ps+pc+pme+pmr=1。 (2) 分阶段遗传算子的引入。研究发现,GA的收敛速度、寻优结果与选择、交叉、变异算子的设置有很大关系。其中,选择算子对算法收敛速度影响较大,交叉、变异算子则对算法寻优结果有重要影响。在算法搜索的不同阶段,合理调整遗传算子,能够使算法性能得到改善。因此,本文对GA作了如下改进: 在算法的初始阶段,设置一个具有较大值的选择算子ps(0.6≤ps<1),目的在于使算法能够在较短的时间内逼近排样问题的最优解或次优解,从而快速获得较好解。此时,由于所设置的交叉算子与变异算子值较小,当算法进行到某个阶段时,可能会陷入局部最优,在某个子空间内反复搜索最优解。为避免算法过早收敛,需对各遗传算子进行调整,将搜索范围延伸至更大的解空间。此时,令算法进入第二阶段搜索过程。在这一阶段,对遗传算子作如下调整:将选择算子 ps设置为一个较小值(0 在算法实际搜索过程中,两个搜索阶段进行切换的判断依据是当前搜索到的最好解的变化情况。通过最好解的变化情况及预设的条件,动态调整遗传算子,使算法循环交替地进入两个搜索阶段。这一处理可使算法不会总受到单一遗传算子左右,搜索过程既能保证快速性也能保证全局性。 3.4 基于改进最低水平线方法与遗传算法的排样优化算法 利用改进GA实现矩形件排样顺序的寻优,并采用改进最低水平线方法实现矩形件排样,可构造完整的矩形件排样优化算法。算法流程图如图5所示。在算法中,改进最低水平线方法被用于对 GA所产生的每代种群中的各个可行解进行矩形件排放,通过计算可行解的适应度来判断解的优劣。两个搜索阶段的切换条件为当前搜索到的最好解是否连续多代没有得到改进,若是则将遗传算子调整为第二阶段的算子,否则设置为第一阶段的遗传算子。 图5 基于改进最低水平线方法与遗传算法的排样优化算法 为评估所提出的排样优化算法的性能,在Visual C++ 2008环境下编程实现该算法,并与文献[9]中提出的排样优化算法进行实验对比(文献[9]采用了基于最低水平线方法与改进GA的排样优化算法)。首先,以文献[9]给出的算例作为测试数据,该算例包含20种不同尺寸的矩形件(总数为59个),板材宽度为400。在仿真实验中,本文算法的相关参数如表1所示,算法中不同搜索阶段的切换条件为:当前搜索到的最好解是否连续5代都未得到改进;算法的终止条件为:迭代次数达到预设的最大迭代次数。 两种算法的优化结果如表2所示,其中,Uavg指算法重复运行50次得到的板材利用率的平均值, Ubest指在50次运算中得到的最佳利用率,Tavg指平均运算时间。 表1 本文算法采用的参数 表2 排样结果数据(I) 从表2可看出,相对于文献[9]算法,本文算法对该算例的优化结果有明显提高,而算法所需运算时间略有增加。为更好地评估算法性能,通过随机方式产生 10组包含数量不等、尺寸不同的矩形件的排样数据进行算法测试。在算法参数不变的情况下,对上述两种算法进行排样对比实验,排样数据及结果如表3所示。 从表3结果可以看出,本文提出的排样优化算法无论是在板材的平均利用率还是最佳利用率方面,均比文献[9]算法有明显提升。从算法运算时间来看,本文算法与文献[9]算法相比略有增加。随着矩形件种类、数量的增加,这种差别相对于实际运算时间而言几乎可忽略不计。这表明,改进后的优化算法能够在保证运算效率的前提下,有效改善排样效果,提高材料利用率。 表3 排样结果数据(II) 本文对基于最低水平线方法的矩形件排样策略作了改进,通过引入启发式规则灵活选择矩形件进行排样,有效利用板材空白区域,避免板材浪费。采用分阶段设置遗传算子的方法改进 GA,改善算法搜索性能,并将算法与改进最低水平线方法相结合,共同求解矩形件排样问题。排样测试数据表明,文中提出的算法能够有效求解矩形件排样问题,不仅在板材利用率方面有明显提升,且算法执行效率较高,适用于现代制造业、加工业的实际生产。 [1] Jakobs S. On genetic algorithms for the packing of polygons [J]. European Journal of Operational Research, 1996, 88(1): 165-181. [2] 刘德全, 藤弘飞. 矩形件排样问题的遗传算法求解[J].小型微型计算机系统, 1998, 19(12): 20-25. [3] Hopper E, Turton B C H. An empirical investigation of meta-heuristic and heuristic algorithms for a 2D packing problem [J]. European Journal of Operational Research, 2001, 128(1): 34-57. [4] Yeung L H W, Tang W K S. A hybrid genetic approach for garment cutting in the clothing industry [J]. IEEE Transactions on Industrial Electronics, 2003, 50(3): 449-455. [5] Wei Lijun, Oon W C, Zhu Wenbin, et al. A skyline heuristic for the 2D rectangular packing and strip packing problems [J]. European Journal of Operational Research, 2011, 215(2): 337-346. [6] Christoforos C, Fleszar K. A constructive bin-oriented heuristic for the two-dimensional bin packing problem with guillotine cuts [J]. Computers & Operations Research, 2011, 38(10): 1443-1451. [7] 龚志辉, 黄星梅. 二维矩形件优化排样算法的改进研究[J]. 湖南大学学报, 2003, 30(3): 47-49. [8] 王金敏, 王保春, 朱艳华. 求解矩形布局问题的自适应算法[J]. 图学学报, 2012, 33(3): 29-33. [9] Liu Haiming, Zhou Jiong, Wu Xinsheng, et al. Optimization algorithm for rectangle packing problem based on varied-factor genetic algorithm and lowest front-line strategy [C]//2014 IEEE Congress on Evolutionary Computation (CEC). Beijing: IEEE, 2014: 352-357. Optimization Algorithm for Rectangle Packing Based on Improved Lowest Horizontal Line Method and Genetic Algorithm Liu Haiming, Zhou Jiong, Wu Xinsheng, Luo Jiaxiang For the issue of rectangle packing problem, traditional lowest horizontal line method might generate certain empty blocks that were not used, which would cause unnecessary waste of material. To solve the problem, heuristic estimate is introduced into search process to achieve rectangle filling for the empty blocks and improve utilization. For optimization packing sequence of rectangles using genetic algorithm, a new strategy of setting different genetic factors by stages of evolution process is applied to improve algorithm performance. The two improved methods are combined in union to solve the rectangle packing problem. The test data of packing show that the proposed algorithm can effectively improve packing results and improve utilization of material. rectangle packing; optimization algorithm; lowest horizontal line; genetic algorithm TP 391.72 A 2095-302X(2015)04-0526-06 2014-10-18;定稿日期:2015-01-12 广东省科技计划资助项目-工业高新技术领域(2014A010104004);中央高校基本科研业务费专项资金重点资助项目(2014ZZ0033) 刘海明(1978–),男,广东陆河人,讲师,博士。主要研究方向为系统优化与调度、计算机辅助设计与优化、智能优化算法与智能系统。E-mail:hmliu@scut.edu.cn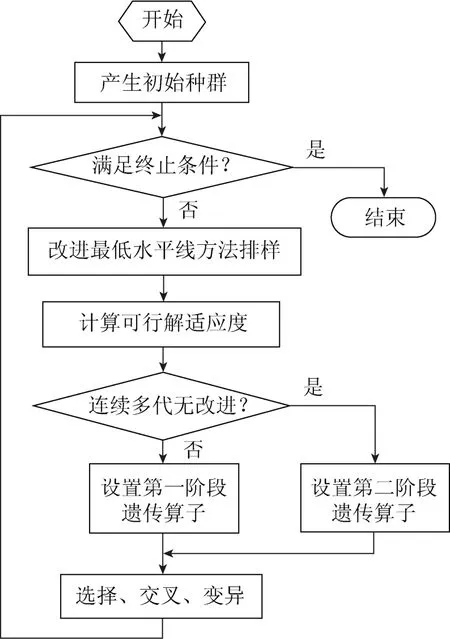
4 算法评估



5 结 论
(School of Automation Science and Engineering, South China University of Technology, Guangzhou Guangdong 510641, China)
——基于人力资本传递机制
——基于反向社会化理论的实证研究
——基于子女数量基本确定的情形

