方差不对称先验信息引导的全局阈值分割方法
龙鹏,鲁华祥
(中国科学院半导体研究所,北京100083)
方差不对称先验信息引导的全局阈值分割方法
龙鹏,鲁华祥
(中国科学院半导体研究所,北京100083)
图像分割是图像分析的关键步骤,其中阈值分割方法是最简单也是应用最广泛的方案。Otsu方法在应用于通用的现实图片时,由于其保持着良好的稳定性和分割目标的形状测度,被认为是最好的方法之一。但是大量研究表明对于2类方差差异很大的图像,其阈值严重偏离最优阈值,而偏向方差大的一类。研究了Otsu最优准则和现有改进算法的特性,进而基于前景与背景方差差异先验信息提出了新的最优化准则。与现存的非类间方差阈值法和对Otsu阈值法进行改进的方法进行比较表明,该方法具有最优的特性,同时不需要可变参数。
Otsu方法;图像分割;方差差异;全局阈值;先验信息
图像分割是图像处理领域最经典的问题,也是图像分析和模式识别的首要问题。在众多的分割方案中,基于区域的阈值分割方案是最古老也是应用最简单与普遍的方法,它的关键在于阈值的选取,非常适用于分割前景和背景具有不同灰度级的图像。全局阈值法可以分为基于直方图峰值检测的方法[1];基于优化准则的方法,如最大类间方差法[2]、最大熵法[3]、最小交叉熵法[4]、最大模糊熵[5]、最小误差法[6]、最大分割图像信息熵[7]等;基于空间灰度分布信息的方法,如矩不变法[8]、局部自适应阈值法[9]、二维Otsu阈值法[10]、三维Otsu阈值法[11]、基于形态学拓扑结构的方法[12]等;基于变换区域的方法,如有效平均梯度法[13];以及基于特定理论的方法,如基于遗传算法的阈值法[14]、前向投影法[15]、基于数据场的方法[16]。在所有的这些方法中,Otsu[2]提出的最大类间方差法表现得最稳定,且无需参数,对于现实图像保持了最好的均匀性和形状特性[17],被商业软件GIMP和学术软件MATLAB采纳为自动阈值法。
但是研究表明Otsu阈值经常偏离理想的阈值[18⁃21]。Lee等[17]研究结果表明,当目标与整幅图像的面积比例为30%时,Otsu分割算法能达到最优分割性能,但随着其相对面积减小直到低于10%以后,Otsu算法的分割性能迅速下降。Xue等[19]研究表明,当对象和背景有相同的概率密度和类内方差时,Otsu方法为最小误差法的特例,不过这一假设在现实情况下并不经常成立,从而影响了Otsu方法和最小误差法的性能。Qiao等[20]研究表明Otsu阈值倾向于将面积大的类分裂,而Medina⁃Carnicerd等[21]则得出相反的结论,原因是文献[20]中,面积大的类具有大的方差,而文献[21]中则正好相反。Xu等[22]总结出Otsu阈值等于2类均值的平均值,因此当2类的方差差异大时,阈值偏向于方差大的一类的均值,但最优阈值往往不是2类均值的平均值。Lee[23]指出仅依赖直方图信息难以确定分割方案,因此针对Otsu阈值对于2类方差差异很大时得不到理想阈值,出现了许多融合了先验知识的改进算法[24⁃30]。早期直方图的第1个谷值被成功地用于分割文本图像[24],因为文字的灰度分布非常紧凑,而背景的灰度值分布非常广泛。Qiao等[20]提出加权调整方差和灰度对比度的准则来获取最优阈值,可以有效地分割一部分前背景方差差异很大的图像。文献[25]通过预先得知的背景在图像中的相对比例来限制目标的灰度范围,与原有的优化准则结合构建新的阈值,成功地用于核磁共振图像和计算机断层扫描图像的分割,优于原有的Otsu方法。Li等[26]采用经验参数,将类内方差的和以及差进行加权,提出了新的准则,实验表明可以实现2类方差差异很大的图像分割。由于理想的阈值应该处于谷值点,Ng等[27⁃28]提出了谷值强调方法,通过将Otsu目标函数和直方图谷值点进行加权,可以有效地分割出面积很小、灰度分布很窄的目标。Cai等[29]提出了一种迭代的阈值分割方案,使用2类均值来限制每一次用于分割的图像的灰度范围,从而不断减小待分割的图像区域,直到最终阈值收敛不变,该方法非常适用于提取弱目标。
本文在基于前景和背景方差先验知识的背景下,提出了新的阈值准则,与现存的经典阈值方法进行纵向和横向比较,展现方法的优越性。结果表明本文的方法对于2类方差差异很大的图像能寻找到最优阈值,优于同类的各种方法。
1 相关工作
1.1 Otsu方法
图1展示了一幅灰度图,它的低灰度级部分分布非常窄。直方图如图2所示,出现比较强烈的偏斜和拖尾分布现象,导致计算出来的阈值分别偏高。

图1 灰度图Fig.1 Grey image

图2 直方图Fig.2 Histogram
基于灰度阈值的Otsu分割方法是按照图像的灰度将图像分为2类,求得使类间方差最大的阈值来进行阈值分割。令待分割图像的像素数为N,共有L个灰度级(0,1,…,L-1),灰度级为i的像素数为ni,则有直方图概率密度pi=ni/N,假设阈值t将图像分成2类C0和C1,则C0和C1分别对应灰度级处于{0,1,…,k}和{k+1,k+2,…,L-1}之间的像素集。设σB(k)表示灰度阈值为k时的类间方差,最佳阈值T是使得类间方差取最大值时的k,即

式中:p1,p2分别是2类的概率密度,m1,m2分别是2类的均值,mg是图像的全局均值。从式(1)可以看出,Otsu方法加权地使用了2类的灰度均值信息和概率密度信息,考虑了2类的分布,在实际的应用中取得了很好的效果。但是类间方差的表达式并没有融入2类的均值差异和方差差异的信息,其准则平等地对待了前景和背景,从而使得对应前景和背景方差差异很大的情况下,Otsu阈值偏离理想阈值。
1.2 改进的Otsu阈值
1.2.1 归一化Otsu方法
Hou等[18]认为最大化类间方差与最优化阈值之间没有必然联系,Otsu对应的类内方差实际上并不是类的方差之和,并提出了归一化的类内方差准则。因为Otsu方法是直接基于2类的绝对均值的距离测度,因此使得阈值偏向于方差大的一类,Hou等[18]提出的方法则是基于2类的相对均值距离,即距离经过类的累积概率归一化,则会弱化方差差异的影响。但在实际应用中,效果并不一定比Otsu准则更优,本文认为这是由于简单的基于累积概率的相对距离,并不能很好地抵消Otsu阈值向方差大的一类的均值的偏移,因为即使2类的方差差异很大,其累积概率密度仍然可能非常接近,这一点从图1灰度图和图2直方图可以看出,前景和背景方差差异很大,但是面积和累积概率密度却相近。
1.2.2 融合两类灰度均值差异的改进方法
Qiao等[20]认为,只考虑类内方差,而不考虑2类的均值差异,不能够取得最优阈值,因此通过一个加权系数α来调整类内方差和均值差异的加权权重。该文将背景和目标的平均灰度值的绝对差融入了Otsu类内方差准则。在实际的应用过程中,权重值必须通过分析对象的比例范围和密度对比度的比例范围的先验知识,或者通过相似图像来训练获取。然而,采用训练的方法很难获取足够鲁棒和通用的参数,而精确的关于前背景面积比例和密度对比度的知识无法获取,虽然文献[20]提出了一个迭代的估计α的方法,也受到不准确的先验知识的限制,分割结果受α的取值非常敏感。当α较小时,得到的阈值较小,而α较大时,获取的阈值较大,并且根据α的取值不同,存在非常大的跳跃。在第3部分的方法比较中,将会根据对象占图像的面积比例以及预估的灰度差异,选择不同的α进行实验,取最好的结果以便表现对比的公平性。
1.2.3 融合两类方差差异的改进方法
Li等[26]认为只考虑类内方差,而不考虑2类的方差差异,不能够取得最优阈值,因此通过一个加权系数来调整归一化的类内方差和它们之间的差异来得到新的准则。通过α控制归一化类内方差和其绝对差异的相对权重。该文献通过了一系列的实验,表明过大或过小的α都会影响分割的效果,而当α处于0.4与0.6之间时,结果取得最优并且稳定,因此推荐了α=0.5作为实际使用该方法时的参数配置,在第3部分的方法比较中,将采用文献[26]推荐的参数。
2 本文的优化准则
2.1 Otsu分割实例
1.2 节中提出的各种方法取得了一定的成功,但在许多的情况下并不能保证获取最优的阈值,而且Qiao[20]和Li[26]的方法有需要调整的经验参数。为了克服这些方法的局限性,首先分析了将Otsu准则用于前景与背景方差不对称的图像分割中所存在的缺陷。Xu等[22]的研究表明,Otsu的阈值等于2类灰度均值的平均值。图2展示了前景方差远远小于背景方差的灰度直方图,Otsu阈值等于65。理想的阈值点应该在30左右,取其为阈值,则背景和对象的灰度均值分别为14.830 7、91.866 3,方差分别为11.407 1、635.412 3,可见两类的方差差异非常大,采用Otsu准则,其阈值会偏向前景,即方差大的类。
2.2 优化准则
图3是Otsu的优化准则随阈值变化的趋势图。其中σB是Otsu方法定义的类间方差,而σB1与σB2分别是与低灰度级类有关的部分和高灰度级类有关的部分,如下:


图3 Otsu阈值优化准则Fig.3 Optimization criterion of Otsu
从图3可知,σB1先于σB2取得最大值,这是因为在最优阈值附近,p的变化非常剧烈。而从图4可以看出m1、m2在t的整个变化过程中,变化比较平缓,尤其是m2在最优阈值点以外,几乎呈直线趋势变化,这说明其变化的速率基本不变。从信息论的角度来看,可以认为在Otsu类间方差的准则中,低灰度级,即方差较小的类携带的信息更多,而高灰度级类携带的信息较少。两者的差异越大,则对Otsu准则的有效影响力的差异越大。据此,提出新的优化准则如式(5)所示:
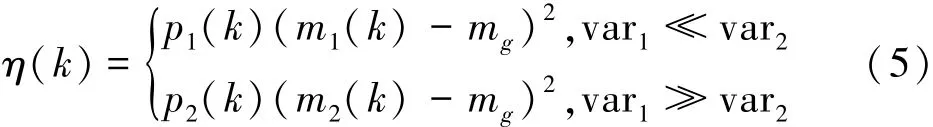
式中:var1和var2代表低灰度级和高灰度级的实际方差,即通过理想的最佳阈值进行分割时两类的方差,它们的实际绝对值不可知,但是通过先验知识可以预判var1与var2的相对大小。当var1远远小于var2时,说明类1所携带的信息对于确定最优阈值更加重要,反之亦然。

图4 灰度均值和概率密度Fig.4 Mean grey level and grey probability
为了验证本准则的有效性以及与同类针对Otsu方法的两类方差差异巨大时失效所提出的改进算法进行比较,本文通过图5的阈值化分割结果进行定性分析,并通过F测度给出了定量的分析结果。

图5 阈值化分割结果Fig.5 Thresholding segmentation results
表1为Otsu方法,1.2中3种改进的方法以及本文的方法对图1的分割阈值和F测度,ground truth是人工分割的结果,如图5(f)所示。从表1可以看出,本文的阈值非常接近直方图的理想谷值点29,图5(e)完整地分割出来对象。Li[26]的方法定量结果也比较接近理想阈值,Qiao[20]的改进方法取α等于0.4,这是为了根据对象占整幅图的面积取的参数,可知与Otsu方法以及归一化Otsu方法结果相差无几,均不能有效地分割出对象。从定量的评估结果F测度也可以看出,本文的方法和Li的方法能较好地分割出对象,其中本文的方法更加精确,与ground truth相比出现的少量空洞也是由于一部分对象像素的灰度分布到了背景中造成。
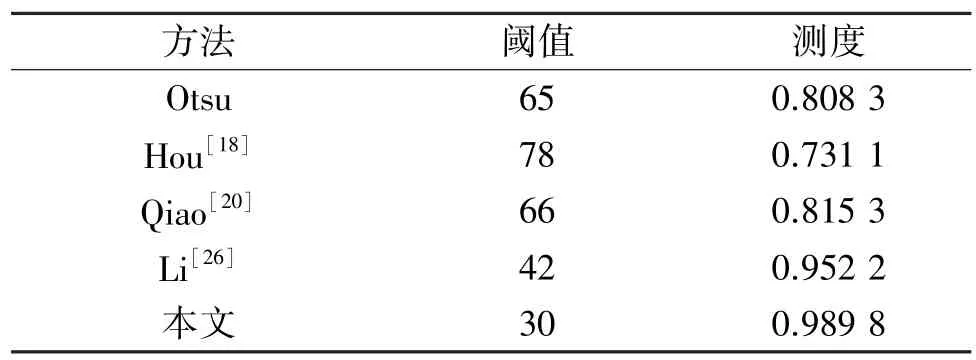
表1 阈值与F测度Table 1 Thresholds and F measures
3 文本与材料图像分割应用
将本文方法分布应用于文本图像,非损害性材料图像分割,实验表明本文方法具有非常实际的应用价值。同时,也将该方法与现存的各种全局阈值法进行比较,有最大熵法[3]、最小交叉熵法[4]、最大模糊熵[5]、最小误差法[6]、矩不变法[8]、归一化Otsu方法[18]、融合两类灰度均值差异的改进方法[20]、融合两类方差差异的改进方法[26]以及Otsu方法。
3.1 文本图像
图6(a)显示了一张车牌图像,图7是对应的直方图,图像来源于文献。可以看出,前景的灰度分布范围非常广泛,理想的阈值分割点在230左右。文献[6]的最小误差法,文献[26]的融合两类方差差异的方法以及本文的方法的阈值分别为244、200、217,其分割结果图最完整的保留了数字与符号,接近直方图的理想均值。同时本文的方法和文献[26]的方法又略优于最小误差法,后者车牌内部的噪声增多,这是由于阈值略偏高。其他的方法所取得的阈值解远远小于最优阈值,所分割得到的字母皆不完整。

图6 不同方法的车牌图像分割结果Fig.6 Segmentation results of license plate using vari⁃ous methods
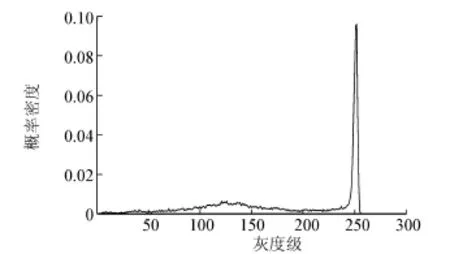
图7 车牌图像直方图Fig.7 Histogram of license plate
3.2 非损害性材料图像
图8(a)显示了一张激光材料图像,图像来源于文献[26],图9是对应的直方图。可以看出,前景的灰度分布范围高度集中,理想的阈值分割点接近250。为了更好地显示分割效果,将分割的轮廓线叠加至原始图像,分割结果如图9所示。从结果可以看出,本文的方法和文献[26]融合背景与前景归一化方差的方法最好地拟合了对象的轮廓,阈值分别为207和211,虽然相比较最小误差法[6],阈值偏离直方图的理想阈值更大,但能够更好地分割出对象。最小误差法分割结果轮廓对目标边界的拟合失败,是因为其阈值接近了最高灰度值。结合3.1文本图像的分割结果也可以看出,最小误差法比较敏感,这主要是因为最小误差法的应用前提是前景和背景都是正态分布。然而往往图像中前景或背景为单边正态分布,使得最小误差法不能取得最优的结果。

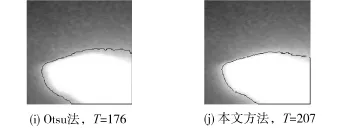
图8 不同方法的激光材料图像分割结果Fig.8 Segmentation results of laser image using various threshold methods

图9 激光材料图像直方图Fig.9 Histogram of laser image
4 结束语
本文方法简单,相比原始的Otsu方法没有引入新的参数,没有增加任何新的计算工作量。在与同类方法进行比较时,具有很好的鲁棒性,而且可以应用于文本图像,材料图像等一系列的图像分割中。但是本方法也存在不足,即对于方差差异不明显的图像并不适用。本文没有讨论对于噪声的鲁棒性,这是因为本文只是提出了一种全局阈值方案,而对于一种全局的阈值方案而不是局部自适应的阈值方案,讨论对于噪声的鲁棒性意义不太。前景和背景方差差异很大的情况在现实中广泛存在,如自然图像图1中的背景灰度级范围小于30,而前景的灰度级范围大于150;车牌图像中背景光处于高灰度级,灰度范围约为10,而前景文字部分的灰度分布从0~230左右;激光材料图像中背景分布在所有灰度级而前景材料目标仅处于最高的灰度级左右。本文提出的方法不一定在一般的图像上优于同类的方法,但是在特定的图像上优于其他全局阈值方法,而且不需要任何经验参数。虽然需要先验知识,但此先验知识易于获取,而且不需要定量的先验知识。正是在先验知识的指导下,反而能取得更好的应用前景。之后的工作将着眼于自动地从图像提取知识进行指导,同时将本方法拓展成通用的全局阈值分割方案。
[1]SEZN M I,TEKLAP A M,SCHAETZING R.Automatic an⁃atomically selective image enhancement in digital chest radi⁃ography[J].IEEE Transactions on Medical Imaging,1989,8(2):154⁃162.
[2]OTSU N.A threshold selection method from gray⁃level histo⁃grams[J].Automatica,1975,11(285⁃296):23⁃27.
[3]PUN T.Entropic thresholding,a new approach[J].Graph⁃ical Models and Image Processing,1981,16(3):210⁃239.
[4]PAL N R.On minimum cross⁃entropy thresholding[J].Pat⁃tern Recognition,1996,29(4):575⁃580.
[5]CHENG H D,CHEN J R,LI Jiguang.Threshold selection based on fuzzy c⁃partition entropy approach[J].Pattern Recognition,1998,31(7):857⁃870.
[6]KITTLER J,ILLINGWORTH J.Minimum error thresholding[J].Pattern Recognition,1986,19(1):41⁃47.
[7]LEUNG C K,LAM F K.Maximum segmented image infor⁃mation thresholding[J].Graphical Models and Image Pro⁃cessing,1998,60(1):57⁃76.
[8]TSAI W H.Moment⁃preserving thresolding:a new approach[J].Computer Vision,Graphics,and Image Processing,1985,29(3):377⁃393.
[9]NIBLACK W.An introduction to digital image processing[M].Birkerood,Denmark:Strandberg Publishing Compa⁃ny,1985:113⁃125.
[10]LIU Jianzhuang,LI Wenqing,TIAN Yupeng.Automatic thresholding of gray⁃level pictures using two⁃dimension Ot⁃su method[C]//1991 International Conference on Circuits and Systems.Shenzhen,China,1991:325⁃327.
[11]景晓军,李剑峰,刘郁林.一种基于三维最大类间方差的图像分割算法[J].电子学报,2003,09:1281⁃1285.JING Xiaojun,LI Jianfeng,LIU Yulin,et al.Image seg⁃mentation based on 3⁃D maximum between⁃cluster variance[J].Acta Electronica Sinica,2003,31(9):1281⁃1285.
[12]SAHA P K,UDUPA J K.Optimum image thresholding via class uncertainty and region homogeneity[J].IEEE Trans⁃actions on Pattern Analysis and Machine Intelligence,2001,23(7):689⁃706.
[13]ZHANG Y J,GERBRANDS J J.Transition region determi⁃nation based thresholding[J].Pattern Recognition Letters,1991,12(1):13⁃23.
[14]YIN Pengyin.A fast scheme for optimal thresholding using genetic algorithms[J].Signal processing,1999,72(2):85⁃95.
[15]BATENBURG K J,SIJBERS J.Optimal threshold selection for tomogram segmentation by projection distance minimiza⁃tion[J].IEEE Transactions on Medical Imaging,2009,28(5):676⁃686.
[16]WU Tao,QIN Kun.Data field⁃based mechanism for three⁃dimensional thresholding[J].Neurocomputing,2012,97:278⁃296.
[17]LEE S U,CHUNG S Y,PARK R H.A comparative per⁃formance study of several global thresholding techniques for segmentation[J].Computer Vision,Graphics,and Image Processing,1990,52(2):171⁃190.
[18]HOU Zujun,HU Qingmao,NOWINSKI W L.On mini⁃mum variance thresholding[J].Pattern Recognition Let⁃ ters,2006,27(14):1732⁃1743.
[19]XUE Jinghao,ZHANG Yujin.Ridler and Calvard’s,Kitt⁃ler and Illingworth’s and Otsu’s methods for image thresh⁃olding[J].Pattern Recognition Letters,2012,33(6):793⁃797.
[20]QIAO Yu,HU Qingmao,QIAN Guoyu,et al.Threshol⁃ding based on variance and intensity contrast[J].Pattern Recognition,2007,40(2):596⁃608.
[21]MEDINA⁃CARNICER R,MADRID-CUEVAS F J.Uni⁃modal thresholding for edge detection[J].Pattern Recog⁃nition,2008,41(7):2337⁃2346.
[22]XU Xiangyang,XU Shengzhou,JIN Lianghai,et al.Char⁃acteristic analysis of Otsu threshold and its applications[J].Pattern Recognition Letters,2011,32(7):956⁃961.
[23]LEE J S,YANG M C K.Threshold selection using esti⁃mates from truncated normal distribution[J].IEEE Trans⁃actions on Systems,Man and Cybernetics,1989,19(2):422⁃429.
[24]WU V,MANMATHA R.Document image clean⁃up and bi⁃narization[C]//Proceedings of SPIE Symposium on Elec⁃tronic Imaging.San Jose,CA,USA,1998:263⁃273.
[25]HU Qignmao,HOU Zujun,NOWINSKI W L.Supervised range⁃constrained thresholding[J].IEEE Transactions on Image Processing,2006,15(1):228⁃240.
[26]LI Zuoyong,LIU Chuncai,LIU Guanghai,et al.A novel statistical image thresholding method[J].AEU-Interna⁃tional Journal of Electronics and Communications,2010,64(12):1137⁃1147.
[27]NG H F.Automatic thresholding for defect detection[J].Pattern Recognition Letters,2006,27(14):1644⁃1649.
[28]FAN Jiulun,LEI Bo.A modified valley⁃emphasis method for automatic thresholding[J].Pattern Recognition Letters,2012,33(6):703⁃708.
[29]CAI Hongmin,YANG Zhong,CAO Xinhua,et al.A new iterative triclass thresholding technique in image segmenta⁃tion[J].IEEE Transactions on Image Processing,2014,23(3):1038⁃1046.
Global threshold segmentation technique guided by prior knowledge with asymmetric variance
LONG Peng,LU Huaxiang
(Institute of Semiconductors,Chinese Academy of Sciences,Beijing 100083,China)
Image segmentation is a fundamental step in image processing,and threshold segmentation is the simplest and most widely used method among the segmentation methods.The classic Otsu method is deemed as one of the best methods for general real world images with regard to uniformity and shape measure.However,a lot of research shows that,for two classes of image with large variance difference,the threshold seriously deviates from the opti⁃mum threshold and inclines to the type with larger variance.In this paper,optimal Otsu criteria and the properties of an existing improved version are analyzed,then a novel criterion of optimization is proposed by combining prior knowledge about the variance discrepancy between background and foreground.The method is compared with the current non⁃between⁃class variance threshold methods and some improved Otsu threshold methods.The results show that our method is optimal,with no need for variable parameters.
Otsu method;image segmentation;variance discrepancy;global threshold;prior knowledge
TP751
A
1673⁃4785(2015)05⁃0663⁃06
10.11992/tis.201412022
http://www.cnki.net/kcms/detail/23.1538.tp.20150930.1556.020.html
龙鹏,鲁华祥.方差不对称先验信息引导的全局阈值分割方法[J].智能系统学报,2015,10(5):663⁃668.
英文引用格式:LONG Peng,LU Huaxiang.Global threshold segmentation technique guided by prior knowledge with asymmetric variance[J].CAAI Transactions on Intelligent Systems,2015,10(5):663⁃668.

龙鹏,男,1990年生,硕士研究生,主要研究方向为医学图像、彩色图像分割、图像检索以及模式分析。

鲁华祥,男,研究员,博士生导师,博士,主要研究方向为半导体神经网络技术及其应用。曾获北京市科学技术进步一等奖、中国科学院盈科优秀青年学者奖、国家发明三等奖,国家“八五”科技攻关重大科技成果奖,95’电子十大科技成果奖。国际首创“半导体人工神经网络硬件及其软件”,“半导体工业生产优化问题的人工神经网络模型、算法与应用”,独创“高精度双权值突触神经元计算机CASSANN⁃Ⅱ”等重大科研成果。
2014⁃12⁃17.
日期:2015⁃09⁃30.
中国科学院战略性先导专项基金资助项目(xda06020700).
龙鹏.E⁃mail:longpeng2008to2012@gmail.com.

