郁闭度模型的建立及应用

陈文灿

（国家林业局华东林业调查规划设计院 浙江杭州 310019）

1 模型形式

郁闭度与乔木平均胸径和林木株数存在相关性，拟建立郁闭度-胸径-株数关系模型的形式如下：

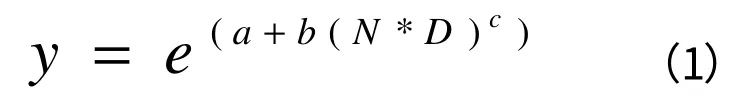
其中，a、b、c为参数；

Y：郁闭度；

N：林木株数；

D：乔木平均胸径。

2 数据准备

2.1 数据来源

以上海市2009年规划设计调查数据为基础，提取乔木林中的樟树数据作为样本。

2.2 偏相关系数的计算与分析

相关系数可用于描述两个变量之间的相关程度，假定乔木平均胸径或林木株数，其中一方为常数时，郁闭度与另外一方之间的相关系数，即为偏相关系数。

偏相关系数的计算公式为：

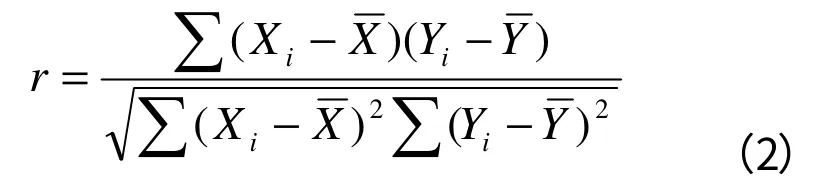
式中，Y为应变量；

X为自变量；

r为偏相关系数。

2.3 郁闭度与乔木平均胸径的偏相关系数

按照单位面积林木株数对样本进行分组，假定10 株为分组单位，样本数小于10 株的就近组合，再按组计算郁闭度与乔木平均胸径的偏相关系数，结果如表1。

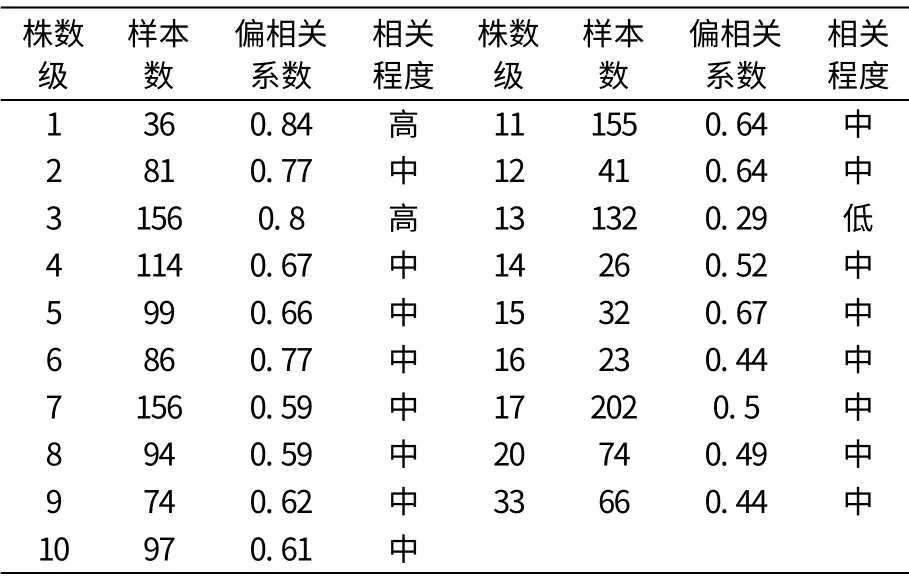
表1 郁闭度与乔木平均胸径的相关程度

假定r≥0.8时相关程度为高，r＜0.3时相关程度为低，其它为中度相关，从表中可以看出，其中两组样本存在高度相关性，一组样本为低度相关，其它均存在相关。

2.4 郁闭度与林木株数的偏相关系数

将样本根据乔木平均胸径的径阶进行分组，样本数小于10 株的就近组合，再按组计算郁闭度与林木株数的偏相关系数，结果如表2。

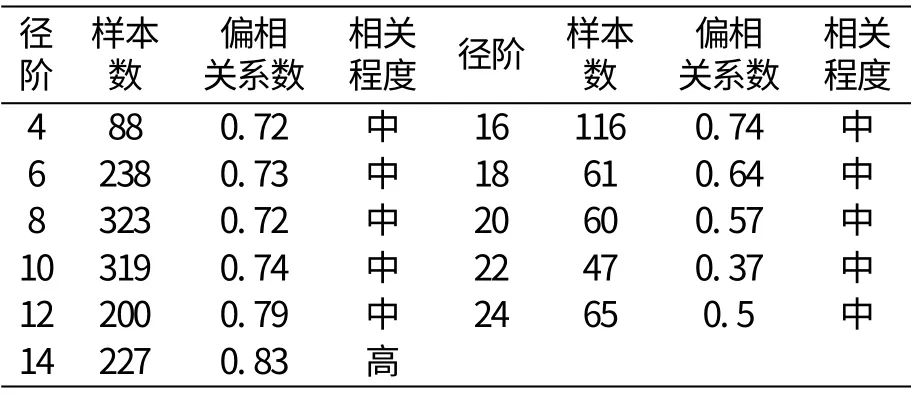
表2 郁闭度与林木株数的相关程度

从表中可以看出，其中一组样本存在高度相关性，其它均存在相关。

偏相关系数分析的结果，郁闭度与乔木平均胸径或林木株数存在相关性，但相关程度不是很高。

3 建模过程

3.1 残差分析

首先对样本进行残差分析，根据《国家森林资源连续清查技术规定》，正常样本的估计区间为：（0，+4σ）其中为残差平方的平均数，超过此范围的样本，作为扰动数据剔除。具体过程如下。

（1）分类建立非线形回归方程，计算各类模型的估计值：

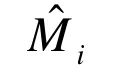
（2）根据样本观察值和估计值计算残差平方：

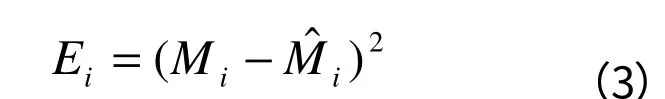
（3）计算残差平方的方差（σ2）：

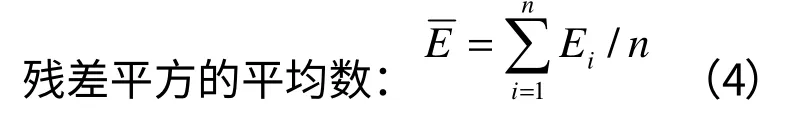
残差平方的方差（σ2）：

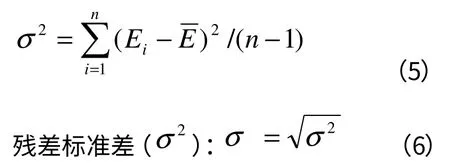
（4）样本剔除

剔除样本中残差平方的平均数超过（0，+4σ）范围的样本，剩余即为建模样本。样本总数为1744 个，属于大样本数据。

表3 郁闭度-胸径-株数关系样本数据

3.2 模型的拟合

使用普通最小二乘法对非线性模型进行拟合，结果为：

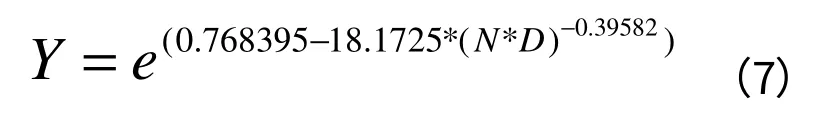
式中，Y：郁闭度；

N：林木株数；

D：乔木平均胸径。

3.3 模型的检验

使用F检验来验证样本估计值和观察值的方差是否存在显著性差异。假设估计值（）和观察值（M）之间符合线性关系，使用普通线性回归方程可以拟合a、b为参数值，具体表达式如下：

式中，a、b为估计参数。

F 检验统计量的计算公式如下：

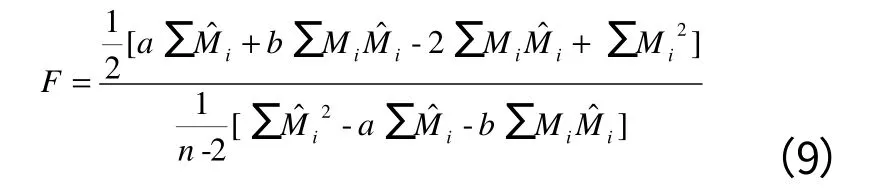
式中：F表示检验统计量；n表示样本数量。

F检验统计量为-804.93，明显小于临界值（Fα=1），说明样本估计值与观察值之间的方差不存在显著性差异，模型适用。

3.4 模型的评价

模型的评价使用了总相对误差、总系统误差、平均相对误差绝对值、估计精度、复相关系数等指标，具体的计算公式如下。

（1）总相对误差

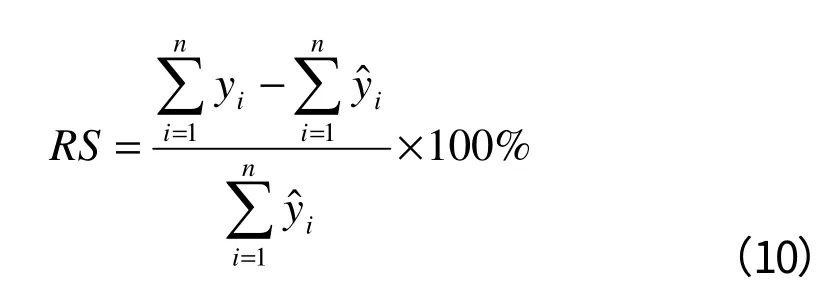
（2）总系统误差

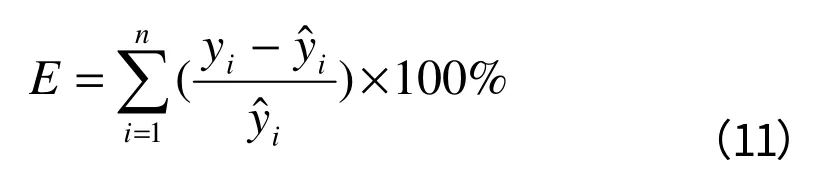
（3）平均相对误差绝对值

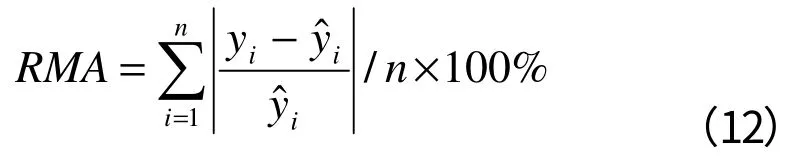
（4）估计精度

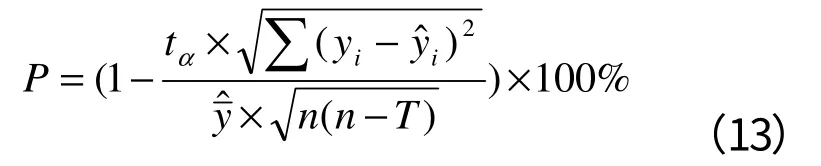
（5）复相关系数

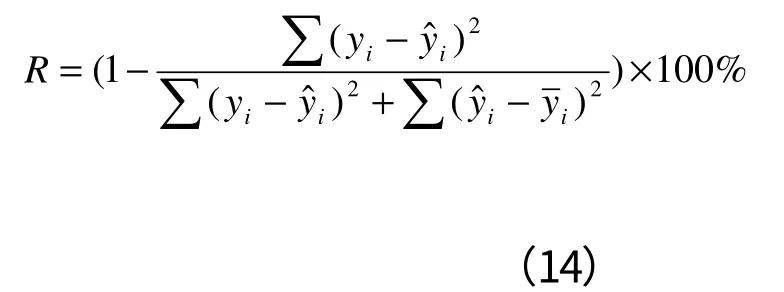
其中：（yi）为观察值；（）为估计值；（n）为样本单元数；（m）自变量个数；（T）为回归模型参数个数；tα表示显著性水平α时的t分布值，具体计算时α值采用0.05。

计算结果，总相对误差为6.99；总系统误差为7.13；平均相对误差绝对值为11.41；估计精度为99.76；复相关系数为66.83。

4 模型的使用

由于郁闭度因子属于目测调查，存在调查误差，同时，林木生长的生态重叠度不同，郁闭度、胸径、单位株数之间的关系变动系数比较大，导致所建模型的复相关系数比较低，所以在使用模型时，将复相关系数作为权重对郁闭度理论值进行修整，具体方法如下：

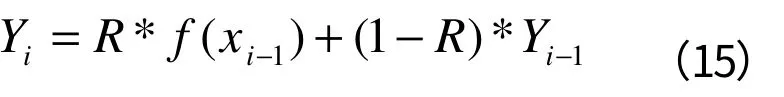
其中：Yi为目标年份的郁闭度；

Yi−1为初始郁闭度；

R为模型复相关系数；

f（xi−1）为模型计算的理论小班郁闭度。

5 样本检验

选取上海市2009年森林资源规划设计调查数据库中符合条件的12825 个小班作为检验样本，检验模型的复相关系数作为权重更新郁闭度时，理论数据与实际调查数据之间的相关程度是否有明显的改善，利用相关系数作为评价指标，复相关系数未参与更新时，理论数据与实际调查数据之间的相关系数为0.7264，为中度相关，复相关系数参与更新时，相关系数为0.8376，提升为高度相关，相关程度有明显改善。

[1] 唐守正.多元统计分析方法[M].北京：中国林业出版社,1984.

[2] 国家林业局.国家森林资源连续清查技术规定[S].2014.[3] 曾伟生，骆期邦，贺东.论加权回归与建模[J].林业科学,1999，35.

[3] 曾伟生，骆期邦，贺东.论加权回归与建模[J].林业科学,1999，35.