具有加速因子的OSEM重建算法用于X射线荧光CT研究

孙鹏飞 邓 彪 杨 群 杜国浩 佟亚军 肖体乔

具有加速因子的OSEM重建算法用于X射线荧光CT研究

孙鹏飞1,2邓 彪1杨 群1杜国浩1佟亚军1肖体乔1,2

1（中国科学院上海应用物理研究所 嘉定园区 上海 201800）
2（中国科学院大学 北京 100049）

有序子集最大期望值算法(Ordered Subsets Expectation Maximization, OSEM)具有较高的图像重建质量和较短的计算时间，已经被应用于内源CT（如SPECT、PET、同步辐射X射线荧光CT）的图像重建中。本文提出了一种具有加速因子的OSEM算法应用于X射线荧光CT的图像重建，通过引入加速因子h来调制校正因子的步长加快OSEM算法的收敛速度，研究了不同加速因子和不同子集数的AOSEM算法对重建图像质量的影响。计算机模拟及实验结果表明，在获得同等质量重建图像的同时，具有加速因子的OSEM算法的重建速度是常规OSEM的两倍。

同步辐射，X射线荧光CT，图像重建质量，有序子集最大期望值算法

X射线荧光CT (X-ray fluorescent computed tomography, XFCT)通过探测样品内某元素受激发射的特征X射线结合CT重建算法重建元素在样品内部的空间分布[1]，具有无损、高分辨等优点。随着第三代同步辐射光源和探测技术的发展，XFCT空间分辨率可达纳米量级，在材料、生物医学等领域的研究得到了广泛应用[2−5]。

目前CT重构常用的方法包括滤波反投影(Filter Back Projection, FBP)和迭代算法。迭代重建算法因其在有限的投影数和噪声影响情况下，能提供比滤波反投影更高质量的重建图像，被广泛应用于投影角度较少的内源CT (SPECT、XFCT)的图像重建中。1982年Shepp等[6]提出了最大似然期望值法(Maximum Likelihood Expectation Maximization, MLEM)，该方法易于实现并可提供很好的重建效果，但收敛速度较慢。为加快收敛速度，Hudson等[7]将有序子集(Ordered Subsets, OS)块迭代的思想应用到MLEM算法上，由此得到的OSEM算法，其每个子集遍历投影数据时都要对图像更新一次，有效地加快了重建速度，被应用于SPECT等内源CT图像重建中[8−9]。上海光源X射线成像组已将OSEM算法应用于XFCT的图像重建中，但图像重建的速度依旧较慢[10−11]，限制了OSEM算法在XFCT中的进一步推广和应用。

本文将通过引入加速因子h来调制校正因子的步长，以改善OSEM算法的收敛特性，进而提高XFCT重建速度。

1 具有加速因子的OSEM算法原理

X射线荧光CT的MLEM重建算法如下[6]：

式中，Ck+1(j)表示测量得到的投影值经过第k+1次迭代后第i个像素的近似值，系数K(i,j)表示像素i对投影强度yj的贡献因子。分母为第k次迭代后的投影估计值：

加速因子h作为指数引入到式(1)：

对式(3)进行泰勒一阶展开，忽略高次项有：

式(4)给出了具有加速因子MLEM算法(Accelerated Expectation Maximization, AEM)。当h=1时为传统MLEM算法；当h＞1时可以起到增大校正因子进而增大重建图像更新步长的作用[12−13]。然而，加速因子h的大小受到图像更新后像素值正负的影响。根据式(1)，MLEM算法重建后的像素可以避免出现负值，但引入加速因子h以后，当h＞1时不能保证的非负性。因此，需要在每次迭代之后加入约束条件[14]：

对于MLEM式(1)，具有自动保持每次迭代总计数守恒的特性。然而，引入加速因子h以后，AEM重建算法无法保持近似解总计数守恒，会引起图像的离散化和变形。为保证MLEM算法这一特性，必须在每次迭代之后加入约束条件：

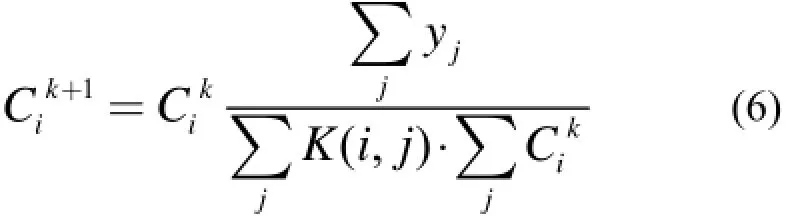
加入约束条件的AEM算法，可以通过有效的增大因子h来加快MLEM算法的收敛速度。根据式(6)，下一次迭代重建结合了本次迭代计算所得的投影值。

Hudson等[15]将投影值等分成若干个有序集合，称为有序子集。一次迭代过程中每个子集都会更新图像一次，所以一次OSEM迭代相当于MLEM算法对图像更新了S次，S为有序子集数。XFCT的OSEM重建公式如下：

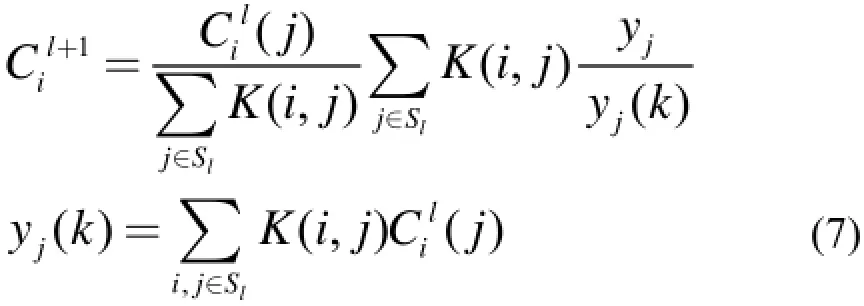
Sl(l=1, 2, …, L)表示有L个子集数，当L=1时为MLEM算法。

具有加速因子的OSEM算法AOSEM公式可以写成：

同AEM，AOSEM算法同样需要在每个子迭代后加入约束条件：

式(8)就是AOSEM算法XFCT迭代重建公式，当加速因子h=1时，为传统的OSEM算法公式，h>1时可以增大校正因子的步长，加快收敛速度。但根据式(8)，如果h取值太大，每次子迭代更新的像素大小都会成为负值被约束为零，所以h的取值具有一定的上限，否则会导致图像的离散化。

2 数字模拟

2.1 数字模型

XFCT模拟实验采用的数字模型由软组织材料和元素Zn组成[16]。Zn元素亮区域的质量分数为0.1%，暗区域为0.05%，其他为软组织材料。数据规模为100×100，每个像素大小为5 μm×5 μm。投影数据的获取：旋转角度采样范围180°，采样间隔为3°；固定投影角下，进行100次平动（步长为5μm），投影数据中加入了泊松噪声，投影总计数约为6.0×108。分别采用OSEM算法、AOSEM算法进行迭代重建，由于Zn元素荧光能量较低，样品自身对其吸收效应较强，所以在重建过程中加入了吸收修正，初始化每个图像的像素大小为0.00001。

2.2 结果与讨论

模拟得到的投影数据采用AOSEM算法和传统的OSEM算法进行不同次数的迭代重建，结果如图1所示。上排为传统的OSEM算法（迭代次数分别为2、4、8、16）；下排为加速因子h=2时的AOSEM算法的重建结果（迭代次数分别为1、2、4、8）。

图1 模拟实验的重建结果：OSEM算法（上排）2、4、8、16次迭代；AOSEM算法（下排）1、2、4、8次迭代Fig.1 Reconstructed result of the numerical phantom: OSEM (top row) with 2, 4, 8 and 16 iterations and AOSEM (bottom row) using h=2 with 1, 2, 4 and 8 iterations.

为研究具有加速因子的OSEM算法的重建效果，视觉比较和归一化的均方根误差方法(Normalized root mean square error, NrMSE)被引入作为评价XFCT图像重建质量的标准，NrMSE公式定义如下：

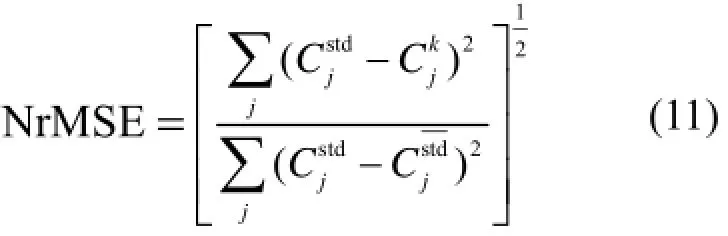
通过视觉观察比较，相同迭代次数下OSEM算法的重建结果要差于本文提出的带有加速因子AOSEM算法。表1给出了两种算法不同迭代次数下的NrMSE值，我们发现OSEM算法迭代2、4、8、16的重建图像的NrMSE值几乎与OSEM算法迭代1、2、4、8相对应。而在相同迭代次数下，AOSEM算法的NrMSE值要小于OSEM算法。因此，我们认为AOSEM算法可以提供与传统OSEM算法相同质量的重建图像，但是所需的迭代次数仅是OSEM算法的一半。

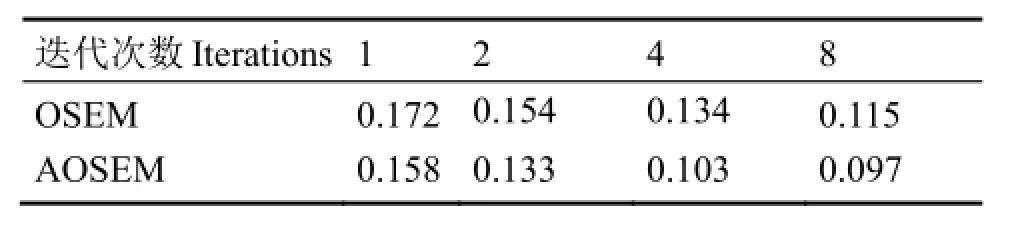
表1 两种算法重建图像的NrMSE值Table 1 NrMSE of the reconstructed images using two algorithms.

在迭代法重建中，介入有序子集是一种加快收敛速度很流行的方法。然而当子集数超过一定值后，重建图像质量反而会随着子集数的增加而降低。这是因为子集数目越多，每个子集内包含的投影数越少，导致重建图像引入过多噪声[15]。所以选取最佳子集数对重建图像结果影响甚大。图2描述了子集数分别为5、10、15、20时，AOSEM算法重建图像与标准图像偏差随迭代次数的变化曲线。相同迭代次数下，随着子集数的增加重建图像的偏差减小，图像收敛速度加快。但当子集数增加到15后，可以看出子集数为15和20时，随着迭代次数的增加NrMSE值变化相当接近，表明图像的收敛速度明显减缓，且子集数继续增加反而会降低图像质量。

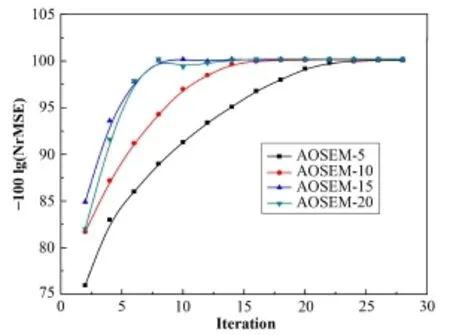
图2 AOSEM算法子集数分别为5、10、15、20时重建结果与标准图像的偏差（迭代次数为2，加速因子h=2）Fig.2 NrMSE vs. iterations for AOSEM with various subset numbers of 5, 10, 15 and 20 (Iteration=2, h=2).

模拟XFCT实验表明，加速因子h具有一定的上限。图3探究了具有不同加速因子的AOSEM算法在不同迭代次数下重建图像的收敛速度。AOSEM算法的子集数选择为10，加速因子h分别取1、1.5、2、2.2、2.5、3，当h=1时为传统的OSEM算法，重建结果显示h＞1的AOSEM算法收敛速度要明显快于OSEM算法，较少迭代次数时加速因子越大重建图像收敛速度越快，这些曲线在多次迭代后趋于同一值。但当h＞3后重建图像会出现严重的离散化。

图3 具有不同加速因子h的AOSEM算法重建结果Fig.3 NrMSE vs. iterations for AOSEM with various accelerated factor (h=1, 1.5, 2, 2.2, 2.5 and 3).

图3中，迭代次数为1时，具有较大加速因子h=2.5、3的AOSEM算法重建结果偏差要大于OSEM算法。这可能是由于在初始迭代，图像的重建值远离收敛值，AOSEM算法导致了这一偏差的放大。解决这一问题可以考虑引入一个合适的初始值，比如将重建速度较快的FBP算法作为AOSEM算法的初始迭代值。当迭代次数增加到5次后，收敛速度并不是随着加速因子而增加，出现了交叉值。取重建图像上圆形线路径上的像素与标准模型进行比较。以圆形线右箭头的起点作为坐标原点，可以得到两种算法重建图像的ROI剖线图，纵坐标为归一化浓度分布，横坐标为圆形线与起点之间的路程。图4(a)为传统OSEM算法、AOSEM算法分别迭代4次的结果与模拟模型的偏差；图4(b)给出了传统OSEM算法迭代8次、AOSEM算法迭代4次与模拟模型的偏差。在同样4次迭代后，AOSEM算法重建结果更接近于模型真实值，尤其在抑制背景噪声和提高ROI边缘像素的更新速度表现更好。而当OSEM算法迭代8次后，与AOSEM算法迭代4次图像的收敛效果相同。因此，获得同等质量的重建结果，AOSEM算法可以节约一半的迭代次数。

图4 两种算法不同迭代次数下剖线图比较(a) OSEM和AOSEM都迭代4次，(b) OSEM迭代8次，AOSEM迭代4次Fig.4 Comparisons of the profiles between the OSEM and AOSEM with various iterations. (a) OSEM and AOSEM both with 4 iterations, (b) OSEM with 8 iterations while AOSEM with 4 iterations

3 实验研究

模拟实验结果证明了AOSEM算法具有较好的重建质量和收敛特性。通过测试样品进一步验证本文提出的算法。测试样品为一个直径10 mm的聚甲基丙烯酸酯圆柱模型。内部含有4个直径为3 mm的孔洞，其中对称排列的两个孔洞被添加了浓度为10−6mol·mL−1的CdCl2溶液[17]，另两个为空。实验在上海光源BL13W1束线站进行，入射光能量为32keV的单色光，照射到样品处的光斑通过狭缝限定为200 μm×200 μm。在数据采集过程中，样品每次转动3°，完成180°范围内的扫描。在固定投影角下，样品平动步长为200 μm，单幅荧光谱的采集时间为3 s。

图5给出了两种重建算法不同迭代次数下Cd的分布。沿着图5(c)中标记的白色线取两种算法分别迭代4次的剖线图，结果如图6所示。由于入射光的能量(32 keV)和Cd元素Kα线能量（约为23 keV）较高，吸收效应影响较弱，从图6中可以看出重建值比较接近真实值。通过比较图5(c)和(e)，AOSEM算法明显具有更高的图像重建质量。另外，图6显示在像素值为零没有Cd元素分布的地方，AOSEM算法重建的像素值更接近于零，含Cd元素区域边界清晰。比较图5(d)和(f)，常规OSEM算法16次迭代的重建结果与AOSEM算法迭代8次获得的图像几乎相近。因此，可以得到与模拟实验相同的结论，具有加速因子的AOSEM算法重建图像质量更好，收敛速度更快，大约可以节省一半的迭代次数。

图5 测试样品验证(a) 测试样品实物图，两个黑色箭头指向的管中放有CdCl2溶液，(b) Cd元素投影数据正弦图，(c)、(d) OSEM算法迭代4次和16次，(e)、(f) AOSEM算法h=2时迭代4次和8次Fig.5 Test sample for validation. (a) Test sample, (b) The sinogram of Cd projection, (c), (d) Reconstructed image of Cd distribution using OSEM with 4 and 16 iterations respectively, (e), (f) Reconstructed image of Cd distribution using AOSEM with 4 and 8 iterations respectively

图6 Cd元素重建像素值比较Fig.6 Comparisons of the profiles along white line between the OSEM and AOSEM algorithm.

4 结语

在XFCT重建中，虽然OSEM算法和MLEM算法比较具有较快的重建速度，但收敛速度依然较慢。本文提出了一种快速重建荧光CT的方法——AOSEM，通过引入加速因子h来加快OSEM算法的收敛速度，当h＞1时相比同阶OSEM算法具有更好的重建图像质量。加速因子h的取值上限也是有所限制的，否则会因为加速过快导致图像的离散化。计算机模拟和测试样品实验结果表明，获得与OSEM算法同等质量的XFCT重建图像，AOSEM算法所需的迭代次数仅是传统OSEM算法的一半。通过比较两种算法重建图像的归一化均方根误差可以得到相似的结论。本文的研究结果表明，具有加速因子的OSEM重构算法可有效提高X射线荧光CT的图像重建速度。

1 Simionovici A, Chukalina M, Günzler F, et al. X-ray microtome by fluorescence tomography[J]. Nuclear Instruments and Methods in Physics Research Section A, 2001, 467(2): 889−892

2 Boisseau P. Determination of three dimensional trace element distributions by the use of monochromatic X-ray microbeams[D]. Massachusetts Institute of Technology, Department of Physics, 1986

3 DeJonge M D, Holzner C, Baines S B, et al. Quantitative 3D elemental microtomography of Cyclotella meneghiniana at 400-nm resolution[J]. Proceedings of the National Academy of Sciences, 2010, 107(36): 15676−15680

4 Takeda T, Wu J, Huo Q, et al. X-ray fluorescent CT imaging of cerebral uptake of stable-iodine perfusion agent iodoamphetamine analog IMP in mice[J]. Journal of Synchrotron Radiation, 2008, 16(1): 57−62

5 Kim S A, Punshon T, Lanzirotti A, et al. Localization of iron in Arabidopsis seed requires the vacuolar membrane transporter VIT1[J]. Science, 2006, 314(5803): 1295−1298

6 Shepp L A, Vardi Y. Maximum likelihood reconstruction for emission tomography[J]. IEEE Transactions on Medical Imaging, 1982, 1(2): 113−122

7 Hudson H M, Larkin R S. Accelerated image reconstruction using ordered subsets of projection data[J]. IEEE Transactions on Medical Imaging, 1994, 13(4): 601−609

8 Dai T, Ma T, Liu H, et al. A high-resolution small animal SPECT system developed at Tsinghua[J]. Nuclear Science and Techniques, 2011, 22: 344−348

9 常城, 谢文晖, 雷贝, 等. SPECT/CT融合显像对肺癌单发骨转移瘤的诊断价值[J]. 核技术, 2013, 36(9): 090301

CHANG Cheng, XIE Wenhui, LEI Bei, et al. SPECT/CT fusion imaging for differential diagnosis of bone solitary metastases in patients with lung cancer[J]. Nuclear Techniques, 2013, 36(9): 090301

10 Yang Q, Deng B, Du G, et al. X-ray fluorescence computed tomography with absorption correction for biomedical samples[J]. X-ray Spectrometry, 2014, 43(5): 278−285

11 Yang Q, Deng B, Lyu W, et al. Fast and accurate X-ray fluorescence computed tomography imaging with the ordered-subsets expectation maximization algorithm[J]. Journal of Synchrotron Radiation, 2012, 19(2): 210−215

12 Zhao X, Hu J, Yang T, et al. An accelerated RAMLA reconstruction algorithm for X-ray cone-beam CT[J]. Insight-Non-Destructive Testing and Condition Monitoring, 2013, 55(5): 237−242

13 Hsiao T, Rangarajan A, Khurd P, et al. An accelerated convergent ordered subsets algorithm for emission tomography[J]. Physics in Medicine and Biology, 2004, 49(11): 2145−2156

14 刘力, 吴朝霞. 具有超松弛因子的OSEM重建算法[J].中国图象图形学报: A辑, 2002, 7(8): 814−817

LIU Li, WU Zhaoxia. OSEM reconstruction with overrelaxation[J]. Journal of Image and Graphics: A, 2002, 7(8): 814−817

15 Hudson H, Larkin R. Accelerated image reconstruction using ordered subsets of projection data[J]. IEEE Transactions on Medical Imaging, 2002, 13(4): 601−609

16 杨群. 快速低剂量X射线荧光CT及其生物医学应用研究[D]. 北京: 中国科学院大学, 2012

YANG Qun. Fast, low dose X-ray fluorescence CT for the biomedical applications[D]. Beijing: University of Chinese Academy of Sciences, 2012

17 Deng B, Yang Q, Xie H L, et al. First X-ray fluorescence CT experimental results at the SSRF X-ray imaging beamline[J]. Chinese Physics C, 2011, 35(4): 402−404

CLC TL99

An accelerated OSEM reconstruction algorithm using an accelerating factor for X-ray fluorescence tomography

SUN Pengfei1,2DENG Biao1YANG Qun1DU Guohao1TONG Yajun1XIAO Tiqiao1,2
1(Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Jiading Campus, Shanghai 201800, China)
2(University of the Chinese Academy of Sciences, Beijing 100049, China)

Background: The Ordered Subsets Expectation Maximization (OSEM) reconstruction algorithm has been widely applied in emission CT reconstruction, such as SPECT, PET and synchrotron radiation X-ray fluorescence CT (XFCT). The quality of reconstructed image is better than other analytical methods such as filtered-back projection algorithm. However, the convergent rate of the OSEM is slow. Purpose: In order to speed up the convergent rate of OSEM, we want to investigate an improved OSEM algorithm. Methods: In this paper, we present an accelerated OSEM algorithm (AOSEM) by increasing the step size of the correction item and show its convergence characteristics with various subsets and accelerated factors. Results: The AOSEM algorithm is proposed and applied in XFCT image reconstruction. Comparing the two reconstruction algorithms, both the simulations and experimental results showed that AOSEM reached the same image quality as in OSEM but only about half the number of iterations when an accelerated factor was used. Conclusion: AOSEM can further speed up the convergence of OSEM when the accelerated factor h＞1.

Synchrotron radiation, XFCT, Construction image quality, OSEM algorithm

TL99

10.11889/j.0253-3219.2015.hjs.38.060201

No.11275257、No.11105213、No.31100680、No.51274054、No.11375257、No.31300480)、国家自然科学基金联合基金重点项

目(No.U1232205/A0802)、CAS-CSIRO合作研究项目(No.GJHZ1303)资助

孙鹏飞，男，1989年出生，2012年毕业于兰州大学，粒子物理与原子核物理

邓彪，E-mail: dengbiao@sinap.ac.cn；肖体乔，E-mail: tqxiao@sinap.ac.cn

2015-01-05，

2015-03-22