基于双向遍历的蒙特卡罗临界计算并行方法

李 静 宋 婧 龙鹏程 刘鸿飞 江 平

基于双向遍历的蒙特卡罗临界计算并行方法

李 静1宋 婧2龙鹏程2刘鸿飞2江 平1

1（合肥工业大学 数学学院 合肥 230009）
2（中国科学院核能安全技术研究所 中国科学院中子输运理论与辐射安全重点实验室 合肥 230031）

在基于蒙特卡罗粒子输运方法的反应堆模拟中，如裂变堆、聚变裂变混合堆等，达到可接受的统计误差需要大量的计算时间，这已成为蒙特卡罗方法的挑战问题之一，需通过并行计算技术解决。为解决现有方法中通信死锁的问题并保证负载均衡性，设计了基于双向遍历的临界计算并行算法。该方法基于超级蒙特卡罗核计算仿真软件系统SuperMC进行实现，以池式钠冷快堆BN600基准模型进行验证，并与MCNP进行对比。测试结果表明，串行和并行计算结果一致，且SuperMC并行效率高于MCNP。

临界，并行计算，蒙特卡罗，SuperMC

近年来层次化并行、跨节点消息通信的多核处理器上的组合线程计算等计算机技术极大地促进了蒙特卡罗方法的发展与在反应堆中的实际应用[1]。然而，在反应堆尤其是复杂先进反应堆[2–6]应用中，蒙特卡罗方法存在巨大的挑战。2012年，Martin[7]对全堆芯蒙特卡罗有效增殖因子(keff)模拟等面临的挑战进行了全面的分析，包括：(1) 达到可接受的统计误差需要大量的计算时间；(2) 海量计算内存；(3) 慢的裂变源收敛；(4) 显示方差不能反映真实方差；(5) 适应未来计算机架构，其中(1)和(2)需要依赖于并行计算技术解决。蒙特卡罗方法天然具有较好的并行粒度，基于蒙特卡罗的反应堆粒子输运计算可分为固定源计算和临界计算。固定源计算按源粒子依次模拟，相互独立，一般能获得较好的并行效率；基于指数迭代法的临界计算需要逐代模拟，每代之间具有相关性，需进行节点及处理器之间的负载均衡才能得到较好的并行效率。

keff是临界计算中最本质的物理量，目前求解时是将基本的中子输运方程转换成指数迭代形式的k特征值方程：

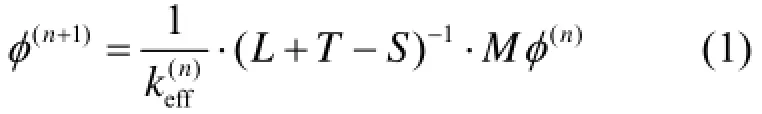
式中，L是泄露运算符；S是内散射运算符；T是碰撞运算符；M是裂变增殖运算符。采用蒙特卡罗方法进行模拟时，从初始假定的值keff(0)和源分布φ(0)开始，采用碰撞、吸收、径迹长度估计及其组合估计等方法来估计某一代的的值，沿粒子径迹抽样下一代裂变源分布并作为下一代初始源迭代直至收敛。

临界计算基于粒子并行的基本思路是：在某代粒子输运过程中，各个计算单元抽样并存储裂变源，该代粒子模拟完后各计算单元将裂变源归并到主计算单元再分配到各计算单元进行下一代计算。该传统方法中，由于部分裂变源粒子是存储在当前计算单元的，因此存在大量不必要的主计算单元与从计算单元之间的粒子通信，降低了并行效率。Romano等[8]进行了方法改进，保留本地产生的裂变源粒子，先计算并存储平均后粒子的序号，据此进行计算单元之间的裂变源粒子传递。

本文在现有方法基础上开展研究，并对其中的通信死锁问题进行改进，介绍了基于双向遍历的临界并行计算算法设计。为保障及检验并行的正确性，对串行随机数按临界特征值计算方法调整随机数序列，介绍相应的方法，并采用基于池式钠冷快堆BN600进行方法的验证对比。

1 临界并行计算算法设计

在计算单元之间进行裂变源粒子传输时，需要通过MPI (Multi Point Interface)进行通信，通信接口采用阻塞模式，相邻计算单元间在通信时进程必须挂起，等待数据传输完成后，两个进程才能进行其它工作。按Romano[8]的算法对每个计算单元进行粒子传输时，当某个计算单元对相邻节点提出的粒子收发需求不能满足时，该计算单元以及和它通信的计算单元的进程将同时挂起，发生死锁。这里以案例说明该情况：假设在使用10个核完成某代keff计算后，产生了总共100个下代源粒子，每个进程源粒子分布依次为：21、5、0、0、10、28、10、3、2、21。1号进程向2号进程传递11个源粒子，2号进程向3号进程传递6个源粒子，此时3号进程拥有6个源粒子，不满足10个粒子的需求，当其向4号进程索取4个源粒子时，3号进程和4号进程将进入死锁状态，程序将停留在该位置。

为避免该问题，本文改为双向遍历的方式，设计的临界计算并行的主要算法仍以上述案例为例，该流程的示意图如图1所示。

(1) 将存储的裂变源粒子广播到所有的计算单元。如果把所有的裂变源粒子存储看作是一个分布在多个计算单元之间的大数组，那么这一步实际上是确定某个处理单元(ith)在该数组中裂变源粒子的开始序号(ai)和结束序号(bi)。

(2) 每个处理单元对存储的裂变源粒子进行模拟，在每个处理单元创建一个单独的数组，用于存储该处理单元模拟粒子过程中抽样产生的下一代裂变源粒子，并更新该处理器中裂变源粒子在整个数组中的编号ai与bi。

(3) 从左向右遍历所有计算单元，并使计算单元仅向右边计算单元发送粒子，仅从左边计算单元接收粒子。即判断：如果bi大于(i+1)N/p，则向右边邻近的处理单元发送bi−(i+1)N/p个裂变源粒子，其中N是该代总的裂变源粒子数；p是处理单元的个数；i是处理单元的序号；如果ai大于iN/p，则从左边邻近的处理单元接收ai−(i+1)N/p个裂变源粒子。

(4) 从右向左遍历所有计算单元，并使计算单元仅向左边计算单元发送粒子，仅从右边计算单元接收粒子。即判断：如果ai小于iN/p，则需要发送iN/p−ai个裂变源粒子到左边邻近的处理器单元；如果bi小于(i+1)N/p，则需要从右边邻近的处理单元接收(i+1)N/p−bi个裂变源粒子。

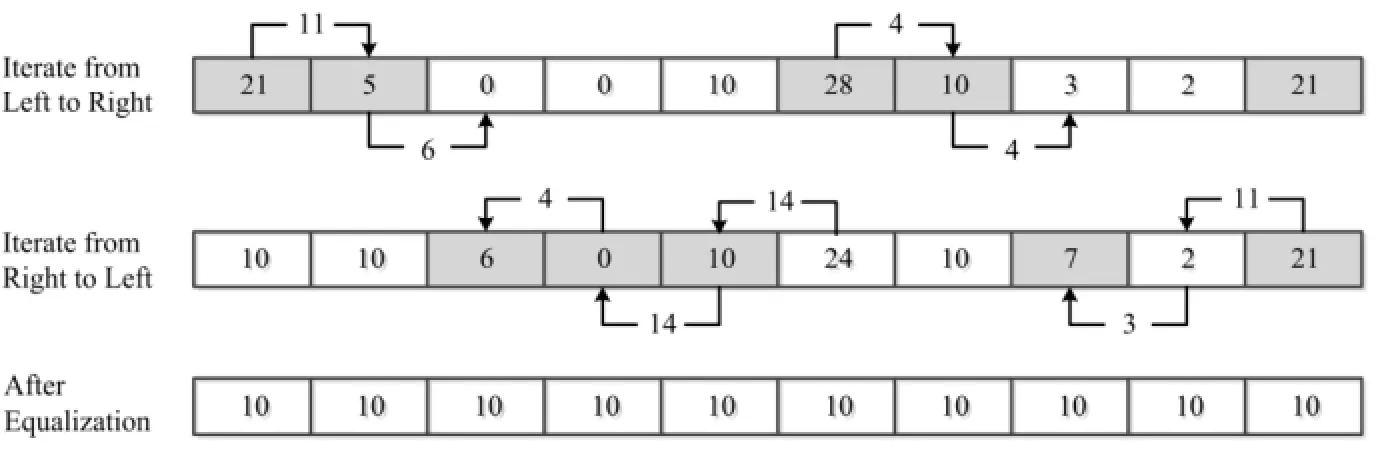
图1 基于双向遍历的临界并行计算流程示意图Fig.1 Flow chart of criticality parallel calculation based on bi-directional traversal.

2 串并行一致的临界计算中随机数调整方法

为保证临界并行计算结果串行和并行一致，本文采用乘同余法和斐波纳契法组合方法产生随机数，并用跳跃法确定每段随机数初始种子。乘同余法的递推公式如下：

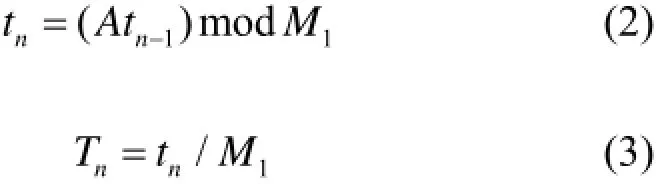
式中，t0为初始种子；M1为模，通常设定为2的整数次幂；Tn为0−1之间均匀分布的随机数。

斐波纳契方法产生随机数递推公式如下：

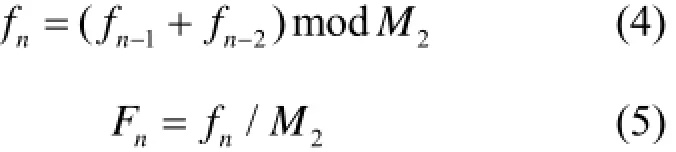
式中，f0和f1为随机数初始种子；M2为模；Fn为0−1区间均匀分布的随机数。

产生的组合随机数序列可表示如下，其随机数周期为258：

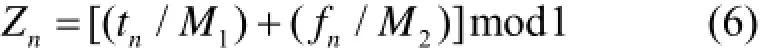
某代模拟时，每个计算单元上裂变源粒子序号相连，对于每个源粒子及其次级粒子使用的随机数最大序列长度固定。开始计算之前需要初始化每个源粒子的随机数种子，即每个计算单元使用的第一个随机数。本文使用跳跃法产生随机数种子：乘同余法随机数利用跳跃法产生随机数种子时，使用式(2)、(3)产生，此时可用式(7)代替进行求模的位运算。斐波纳契方法随机数利用跳跃法产生随机数种子时，先使用式(8)斐波纳契通项公式算出第n项和n−1项随机数值，再代入式(9)得到。最后使用式(6)得到组合随机数的种子。

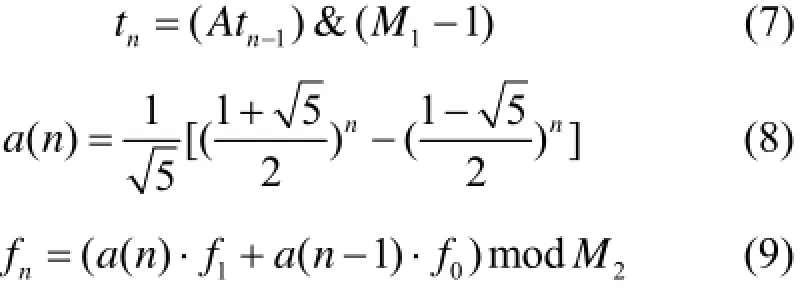
3 池式钠冷快堆BN600基准模型验证

上述方法在超级蒙特卡罗核模拟软件SuperMC[9–13]中进行实现，并采用BN600基准模型进行验证。BN600[14]是俄罗斯的池式钠冷商用快堆，其热功率为1 470MW，电功率为600MW。本文采用国际原子能机构(International Atomic Energy Agency, IAEA)发布的BN600基准模型进行程序验证，图2为BN600在SuperMC中的轴向视图和径向视图。BN600的306个氧化铀燃料组件依富集度布置在4个区：低富集度的内外两个区(Low Emission Zone, LEZ)、中间的中等富集度区(Middle Emission Zone, MEZ)和外面的高富集度区(High Emission Zone, HEZ)。在MEZ和HEZ之间还有一个MOX燃料区（90个燃料组件）。有19根补偿棒(Shim rod, SHR)插入到堆芯的中心平面，6根安全棒(Safety control rod, SCR)提出堆芯平面以上5.5cm。堆芯径向外侧有300个不锈钢反射层组件，最外侧是102个碳化硼屏蔽组件。其详细的几何布置、各区材料、几何尺寸描述见文献[15]。

图2 BN600模型在SuperMC中的径向视图与轴向视图 (a) 径向视图，(b) 轴向视图Fig.2 Radial and axial view of BN600 model in SuperMC. (a) Radial view, (b) Axial view

使用2.2GHz 4核处理器，2×1 000M以太网，单节点32核的高性能计算集群进行测试，每代模拟十万个粒子，共计算500代，选择相同的数据库进行对比测试。SuperMC串并行计算结果一致，keff均为1.01708(0.00005)，MCNP串并行结果一致，keff均为1.01709(0.00004)。其中，MCNP并行设计模式是主从设计模式(Master/Slave)：Master节点只负责任务平均分发（几何信息、计数信息、材料信息等）和结果汇总；Slave节点负责计算各自的任务。Master-Slave Algorithm基本满足临界并行计算的需要，但存在两个问题：一是无效的通信耗时太多；二是需要耗费很大的缓冲空间，这些问题会随着计算任务和计算核数的增加更加明显[15]。相比Master/Slave算法，双向遍历算法减少了大量的无效通信传输，减少了每代计算完成后的平均下代粒子的耗时。并且随着计算负载和计算核的增加，该算法仍能保证很好的性能。表1为SuperMC和MCNP在不同核数下的并行效率对比，得出基于本文方法的SuperMC并行效率高于MCNP。

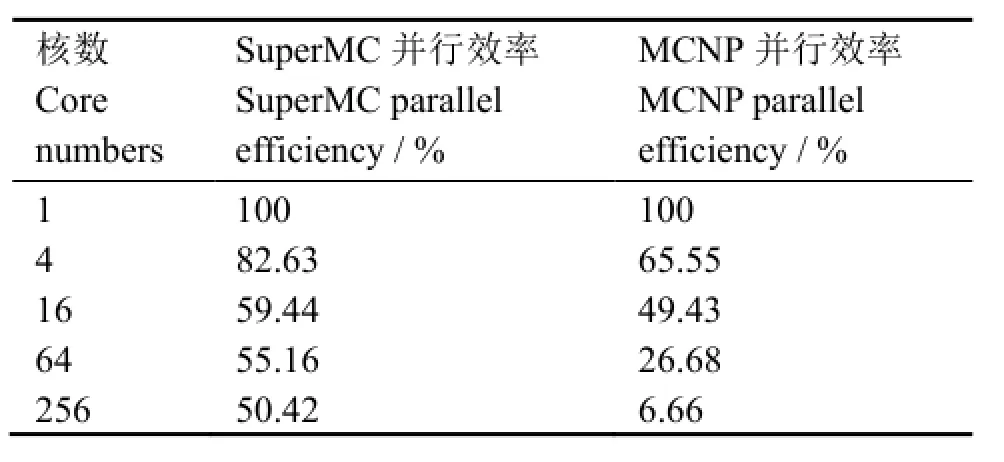
表1 BN600例题SuperMC与MCNP并行效率对比Table 1 Comparison of parallel efficiency of SuperMC and MCNP with BN600.

4 结语

本文对临界计算并行方法开展研究，设计了基于双向遍历的并行方法，并采用俄罗斯池式钠冷商用快堆BN600模型进行校验。keff计算结果串并行一致，说明了本方法与实现的正确性；SuperMC计算的并行效率高于MCNP，说明本方法的有效性及更好的可扩展性。

致谢 感谢中国科学院核能安全技术研究所FDS团队其他成员对本文工作的支持帮助。

1 Brown F B. Recent advances and future prospects for Monte Carlo[J]. Progress in Nuclear Science and Technology, 2011, 2: 1–4

2 Wu Y, FDS Team. Conceptual design activities of FDS series fusion power plants in China[J]. Fusion Engineering and Design, 2006, 81(23–24): 2713–2718

3 Wu Y, Qian J, Yu J, et al. The fusion-driven hybrid system and its material selection[J]. Journal of Nuclear Materials, 2002, 307–311: 1629–1636

4 Wu Y, FDS Team. Fusion-based hydrogen production reactor and its material selection[J]. Journal of Nuclear Materials, 2009, 386–388: 122–126

5 Wu Y, Jiang J, Wang M, et al. A fusion-driven subcritical system concept based on viable technologies[J]. Nuclear Fusion, 2011, 51(10): 103036

6 Wu Y, FDS Team. Conceptual design of the China fusion power plant FDS-II[J]. Fusion Engineering and Design, 2008, 83(10–12): 1683–1689

7 Martin W R. Challenges and prospects for whole-core Monte Carlo analysis[J]. Nuclear Engineering and Technology, 2012, 44(2): 151–160

8 Romano P K, Forget B. Parallel fission bank algorithms in Monte Carlo criticality calculations[J]. Nuclear Science and Engineering, 2012, 170(2): 125–135

9 Wu Y C, Song J, Zheng H Q, et al. CAD-based Monte Carlo program for integrated simulation of nuclear system SuperMC[J]. Annals of Nuclear Energy, 2014, 8: 58–65

10 Wu Y, FDS Team. CAD-based interface programs for fusion neutron transport simulation[J]. Fusion Engineering and Design, 2009, 84(7–11): 1987–1992

11 Li Y, Lu L, Ding A, et al. Benchmarking of MCAM4.0 with the ITER 3D model[J]. Fusion Engineering and Design, 2007, 82: 2861–2866

12 Hu H, Wu Y, Chen M, et al. Benchmarking of SNAM with the ITER 3D model[J]. Fusion Engineering and Design, 2007, 82: 2867–2871

13 Wu Y, Xie Z, Fischer U. A discrete ordinates nodal method for one-dimensional neutron transport calculation in curvilinear geometries[J]. Nuclear Science and Engineering, 1999, 133(3): 350–357

14 IAEA. BN-600 hybrid core benchmark analyses[R]. Austria: IAEA-TECDOC-1623, 2010

15 Brown F B, Goorley J T, Sweezy J E. MCNP5 parallel processing workshop[R]. ANS Mathematics & Computation Topical Meeting, 2003

CLC TL329.2

Parallel computing method of Monte Carlo criticality calculation based on bi-directional traversal

LI Jing1SONG Jing2LONG Pengcheng2LIU Hongfei2JIANG Ping1
1(School of Mathematics, Hefei University of Technology, Hefei 230009, China)
2(Key Laboratory of Neutronics and Radiation Safety, Institute of Nuclear Energy Safety Technology, Chinese Academy of Sciences, Hefei 230031, China)

Background: It requires much computational time with acceptable statistics errors in reactor simulations including fission reactors and fusion-fission hybrid reactors, which has become one challenge of the Monte Carlo method. Purpose: In this paper, an efficient parallel computing method was presented for resolving the communication deadlock and load balancing problem of current methods. Methods: The parallel computing method based on bi-directional traversal of criticality calculation was implemented in super Monte Carlo simulation program (SuperMC) for nuclear and radiation process. The pool-type sodium cooled fast reactor BN600 was proposed for benchmarking and was compared with MCNP. Results: Results showed that the parallel method and un-parallel methods were in agreement with each other. Conclusion: The parallel efficiency of SuperMC is higher than that of MCNP, which demonstrates the accuracy and efficiency of the parallel computing method.

Criticality, Parallel computing, Monte Carlo, SuperMC

TL329.2

10.11889/j.0253-3219.2015.hjs.38.060602

中国科学院战略性先导科技专项(No.XDA03040000)、国家ITER 973计划(No.2014GB112001)、国家自然科学基金(No.91026004)资助

李静，女，1989年出生，2015年于合肥工业大学获硕士学位，计算数学专业

宋婧，E-mail: jing.song@fds.org.cn

2015-01-29，

2015-03-20